轴承摩擦力作用下弹性支承轴系自激振动特性研究

覃文源， 覃 会， 郑洪波， 张振果， 张志谊

(1.上海交通大学 机械系统与振动国家重点实验室，上海 200240；2.高新船舶与深海开发装备协同创新中心，上海 200240)

轴承摩擦力作用下弹性支承轴系自激振动特性研究

覃文源1,2， 覃 会1,2， 郑洪波1,2， 张振果1,2， 张志谊1,2

(1.上海交通大学 机械系统与振动国家重点实验室，上海 200240；2.高新船舶与深海开发装备协同创新中心，上海 200240)

以重力式水洞中的弹性支承轴系为研究对象，研究其在水润滑橡胶轴承摩擦力作用下的自激振动特性及其机理。实验结果表明，系统于某一确定转速产生自激振动，并随转速下降维持不变直到一个较低转速由于驱动力不足而消失，各个转速下的自激振动均表现为转速调制下的单阶模态失稳。为了研究自激振动机理，建立了弹性支承轴系动力学模型。在建模时，将轴系分为弹性支承和转轴两个子结构，分别获取固有振动频率和模态振型，建立在轴承界面摩擦力作用下的支承-转轴耦合动力学模型，并采用模态叠加法对模型进行降阶处理。采用四阶Runge-Kutta方法求解动力学方程，分析主要物理参数对系统的影响。分析结果表明，失稳模态为支承的小阻尼扭转振动模态，支承振动与轴承摩擦耦合作用是系统失稳的主要原因。

弹性支承；摩擦激励；耦合振动；自激振动

水润滑橡胶轴承被广泛用于船舶的艉轴支承[1-3]。由于螺旋桨的悬伸布置，在开、停机以及低速重载工况下，艉轴承-轴颈间往往处于“边界润滑”或“混合润滑”状态，甚至直接接触。在无明显外激励作用下，系统仍可能产生异常振动和鸣音，加速橡胶轴承磨损，影响舰船的隐身性能[4-9]。

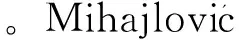
1 弹性支承轴系

1.1实验台简介

重力式水洞弹性支承轴系如图1所示，主要由伺服电机、推力轴承、弹性中间支承以及艉支承组成。其中，艉支承界面如图2所示，四根支承剑的一端与橡胶轴承套铰接，另一端固支，且受预紧力FP作用。

(a)

(b)

1.2实验结果

待水洞灌满水后，对系统进行摩擦振动实验，调节主轴转速由高到低连续变化，从600 r/min开始按30 r/min的间隔逐步下降至30 r/min，拾取各个转速下艉支承水平方向剑固支端的动态支反力。测试结果表明，当主轴转速降至210 r/min时，系统有自激振动现象产生，当主轴转速降至180 r/min时，人耳可以听到自激振动产生的噪声，随着主轴转速的进一步降低，自激振动变得更加强烈，但当主轴转速降至30 r/min时，自激振动难以维持，由于轴颈-轴承摩擦激励引起的能量损耗难以得到持续补偿，电机驱动力不足。这里仅列出120 r/min、60 r/min以及30 r/min时的支反力测试结果，分别如图3～5所示，其中，图3～4中的上、下图分别代表艉支承左、右剑的支反力测试结果。

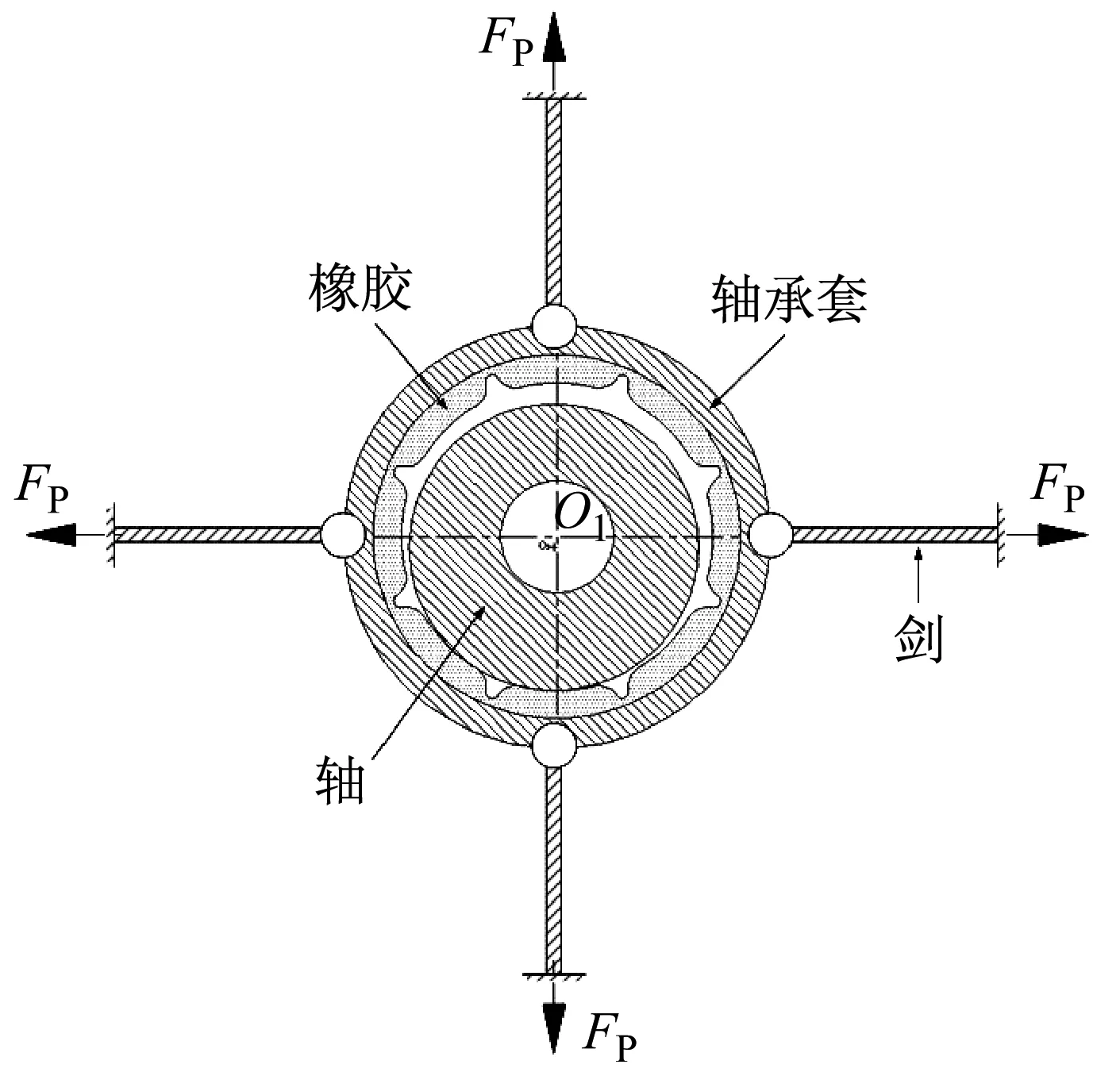
图2 艉支承示意图

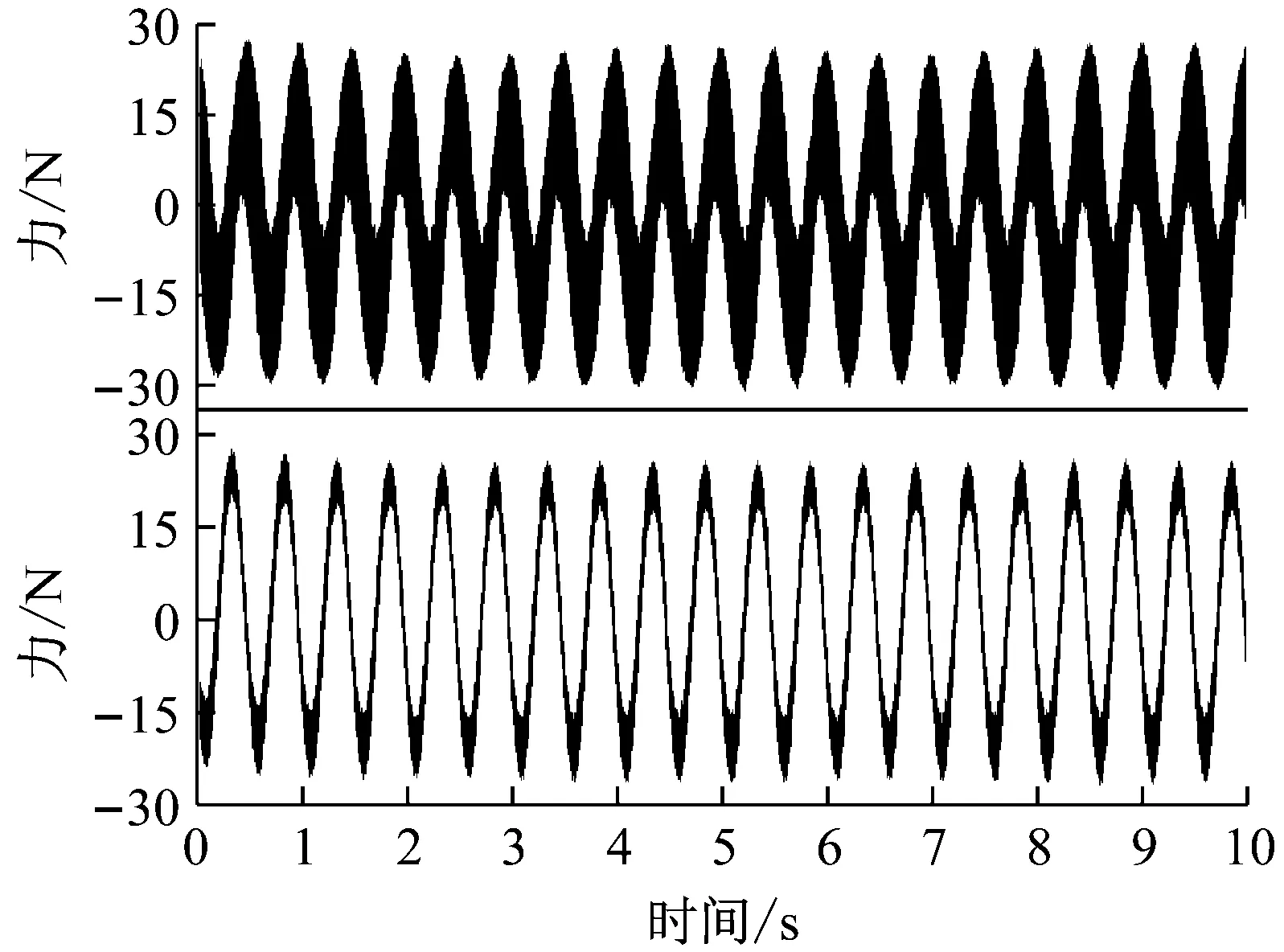
(a) 时域图

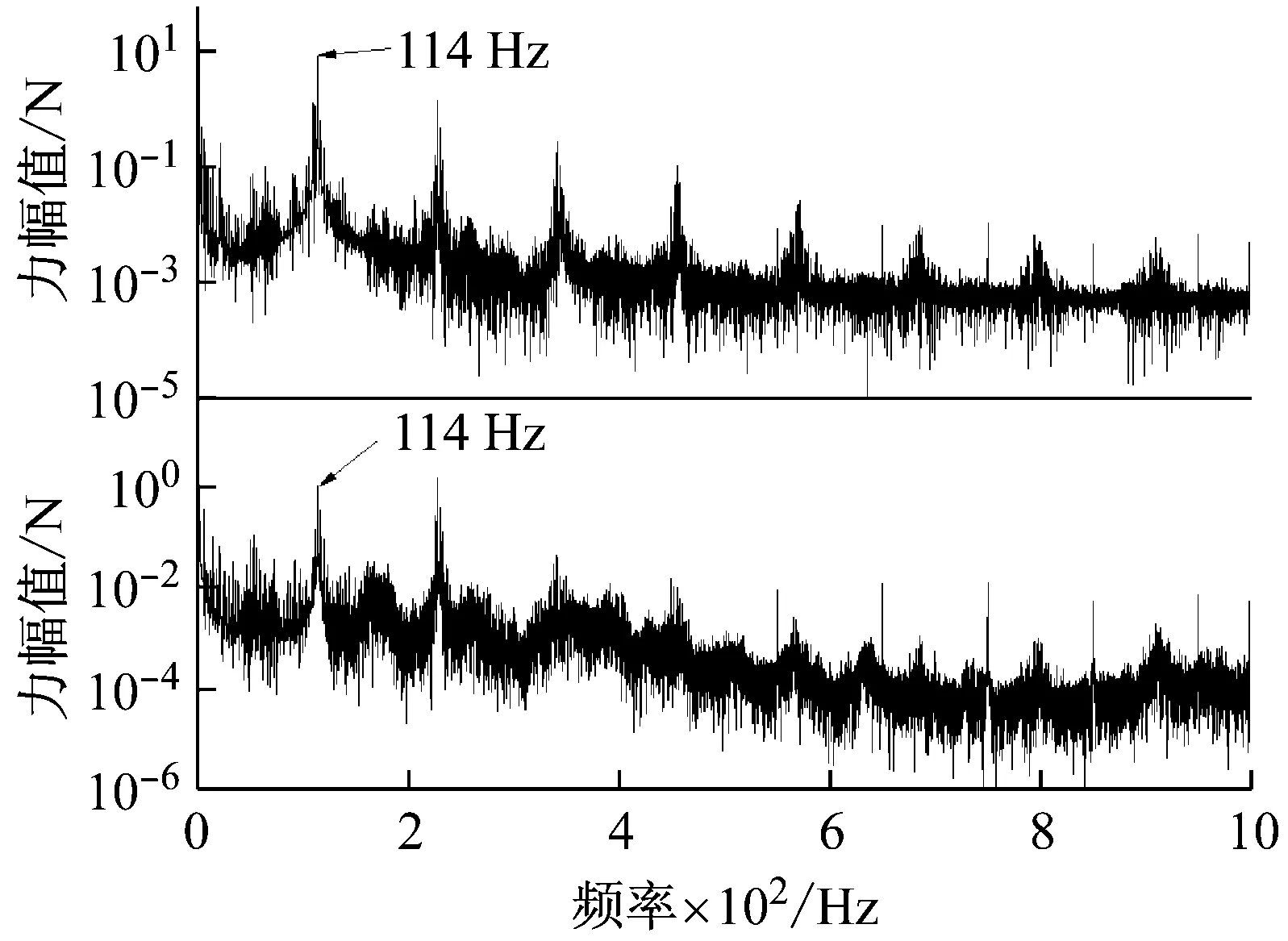
(b) 频率图

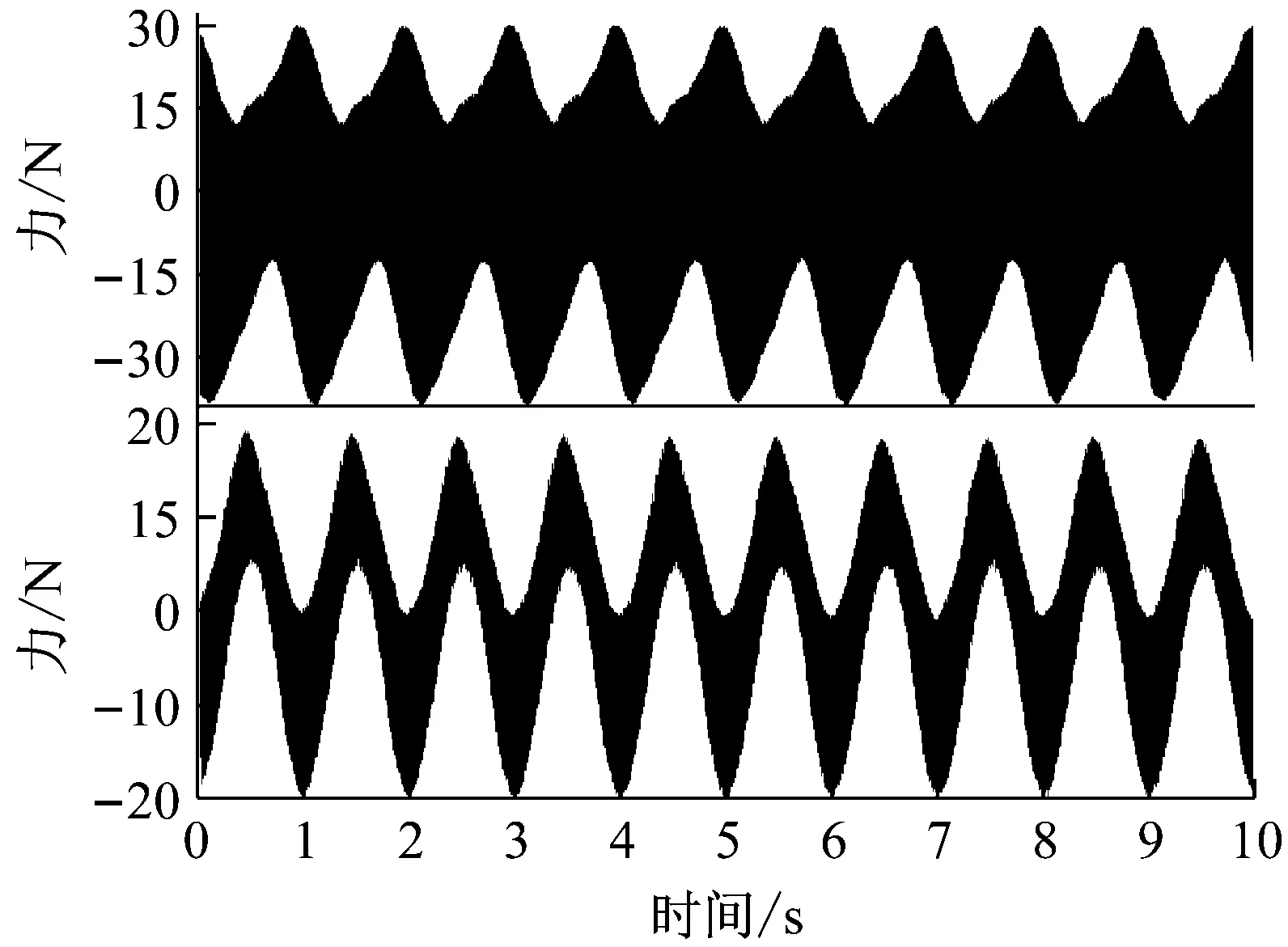
(a) 时域图

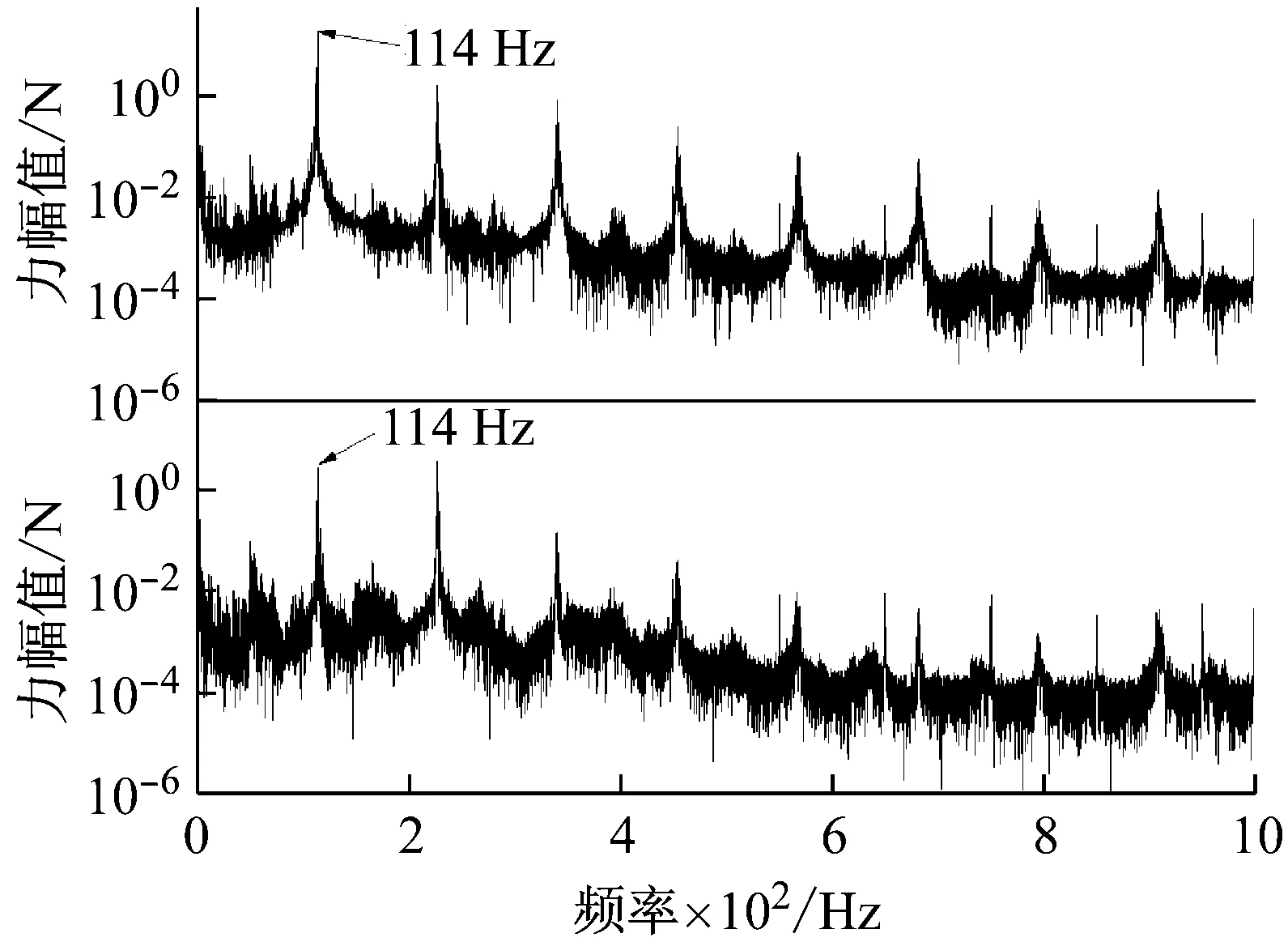
(b) 频率图

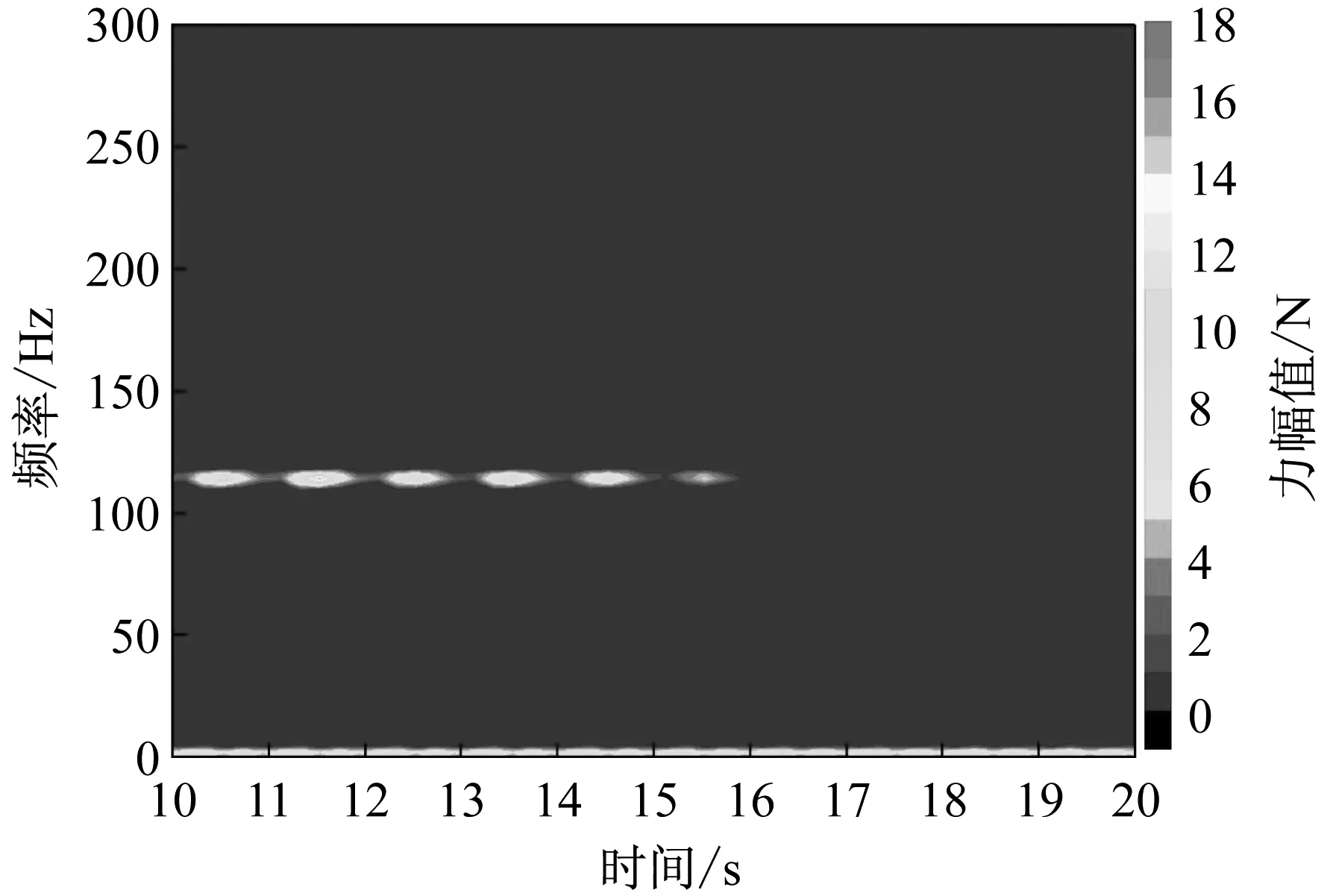
图5 艉支承支反力(30 r/min)

系统自激失稳的频域特征均表现为被主轴转速调制的单阶模态失稳，其频率值约为114 Hz及其倍频。

2 有限元建模

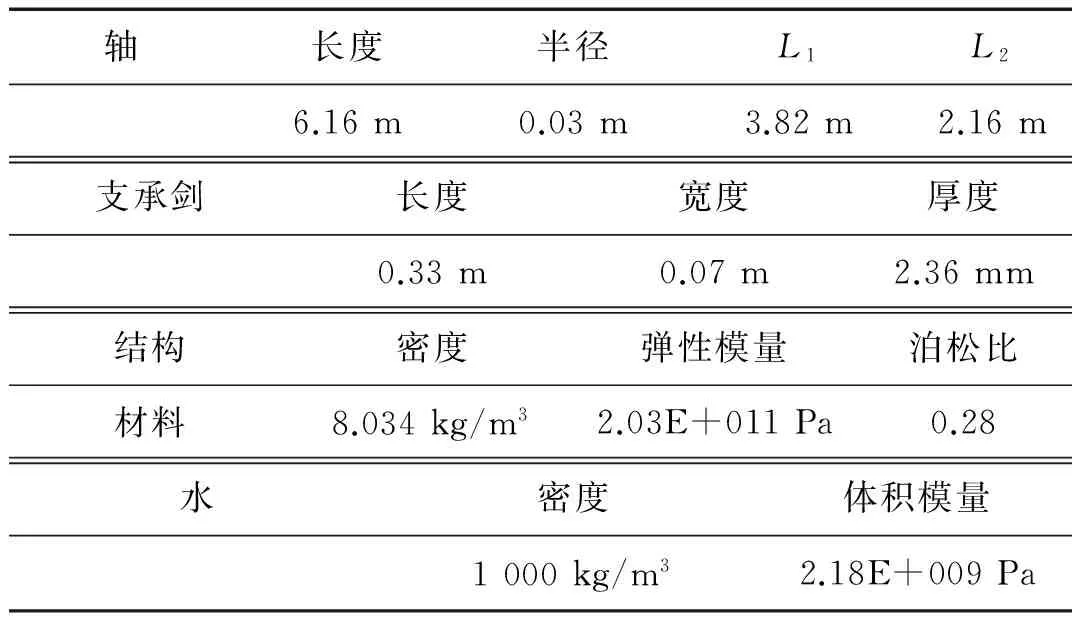
为了分析确定系统的自激失稳模态，利用Abaqus建立系统的流固耦合有限元模型并进行模态分析。其中，模型如图6所示，模型参数如表1所示。流体和转轴均采用实体单元，轴承套和支承剑采用壳单元建模，流体边界条件为平面无反射，支承剑一端与轴承套铰接，另一端固支且固支端有预紧力FP=1 700 N作用。

艉支承的前六阶固有振型如图7所示，其中，第一、三、五、六阶模态是支承扭转振动模态，第五阶模态与失稳模态相对应。

(a) 流固耦合模型

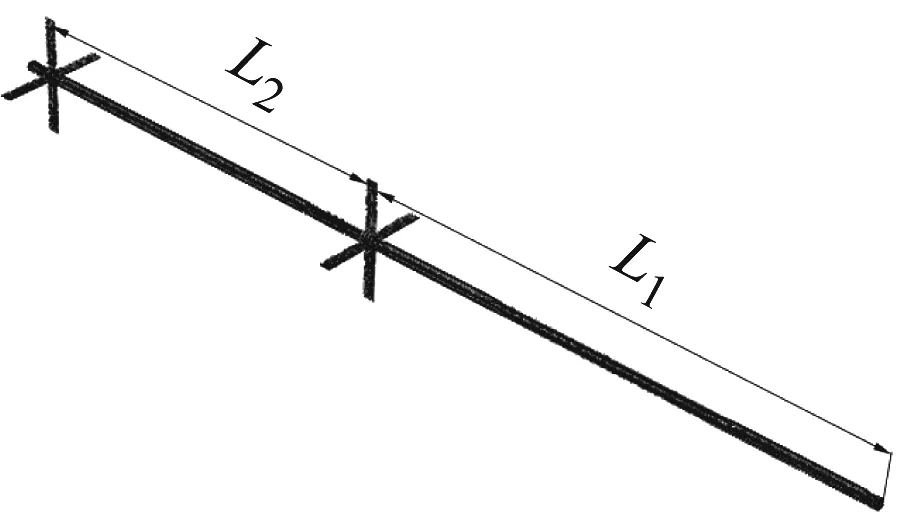
(b) 结构模型

轴长度半径L1L26.16m0.03m3.82m2.16m支承剑长度宽度厚度0.33m0.07m2.36mm结构密度弹性模量泊松比材料8.034kg/m32.03E+011Pa0.28水密度体积模量1000kg/m32.18E+009Pa

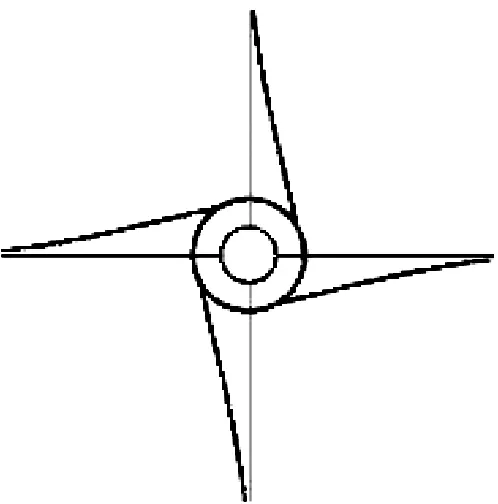
1st 7.1 Hz

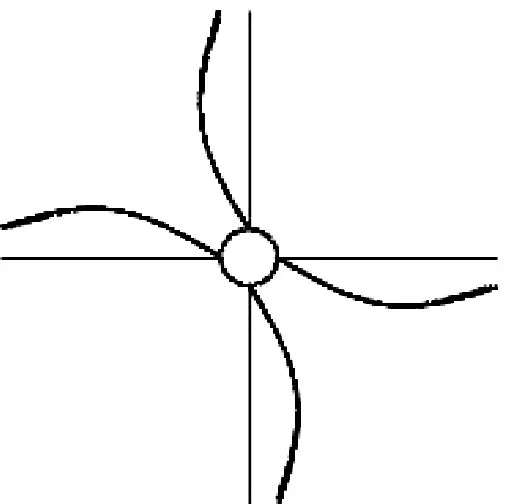
2nd 30.0 Hz

3rd 37.1 Hz

4th 80.0 Hz

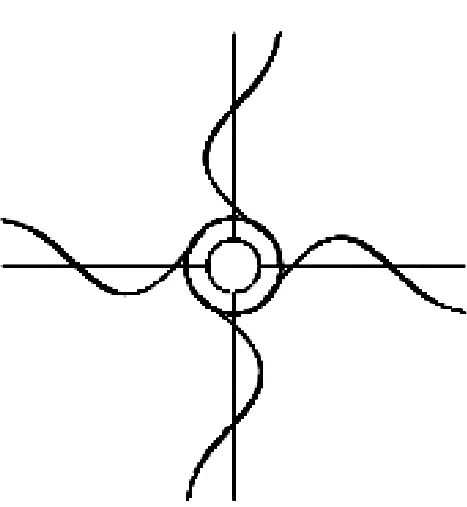
5th 113.6 Hz

6th 265.9 Hz

3 动力学建模

为了进一步分析自激失稳机理，分析艉支承振动对系统振动特性的影响，对如图8所示的系统简化模型进行动力学建模。其中，螺旋桨简化成集中质量，中间支承与推力轴承均以简支代替。简化系统的艉支承界面如图9所示，轴承被简化成并联的线性弹簧和黏性阻尼器。

在进行系统动力学建模时，采用子结构综合方法，将系统分成支承和转轴两个子结构，然后，根据协调条件和边界条件分别求取固有振动频率及其模态，最后，建立通过轴承界面摩擦耦合的支承-转轴耦合动力学模型。

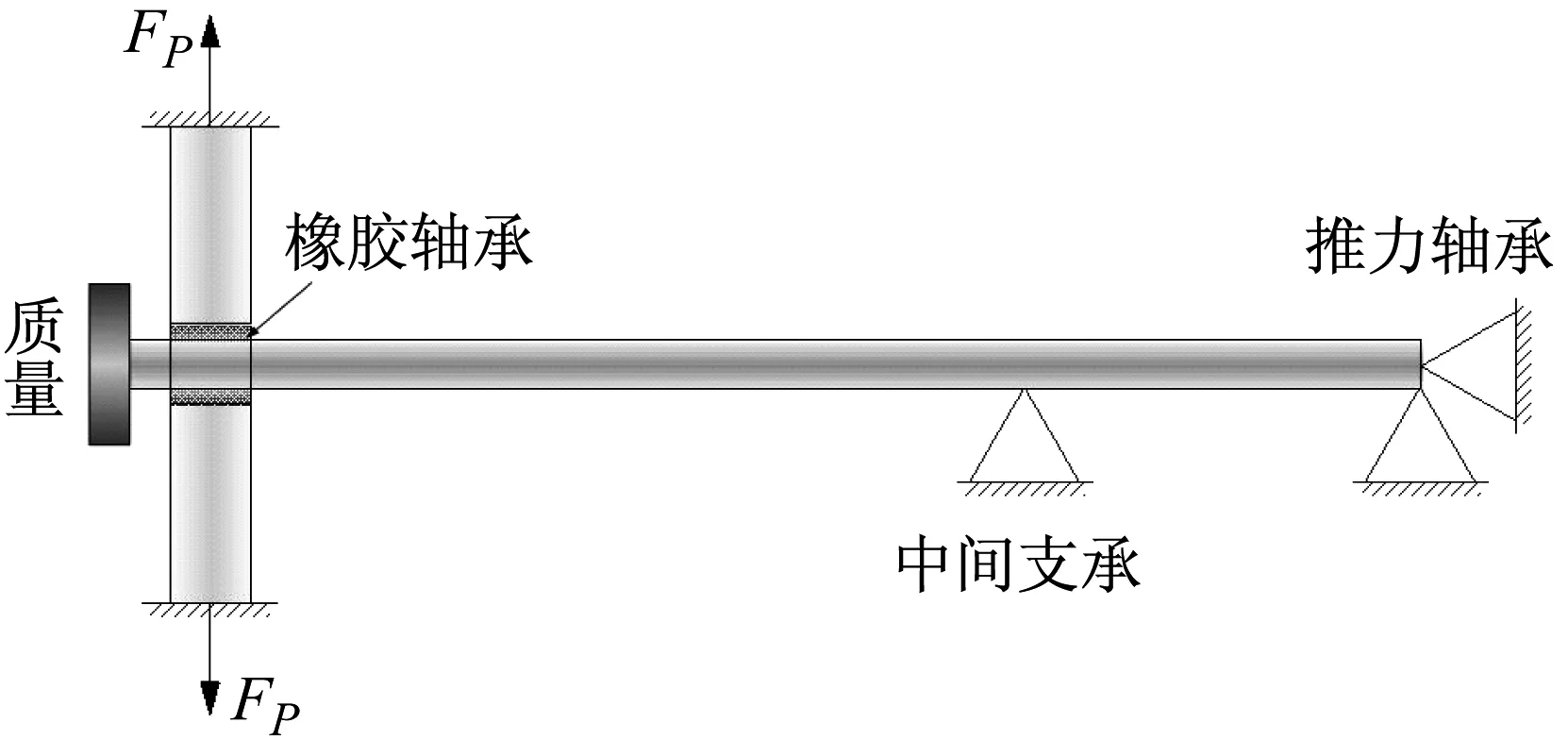
图8 系统简化模型

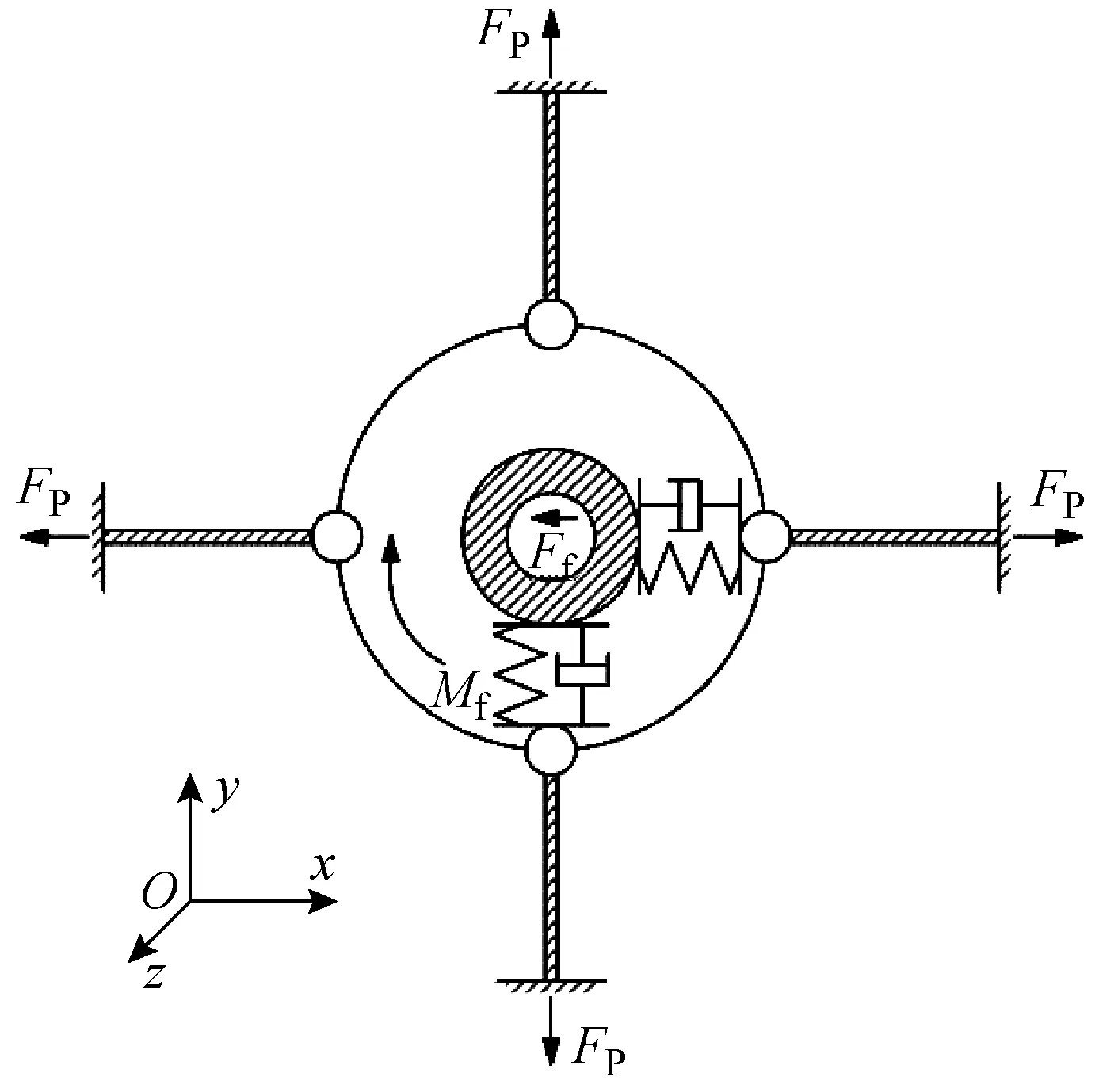
图9 简化系统艉支承界面

艉支承子结构如图10所示，四根支承剑依次标记为1、2、3、4。相对于支承剑，轴承套具有较大的刚性，故将轴承套简化成刚体。

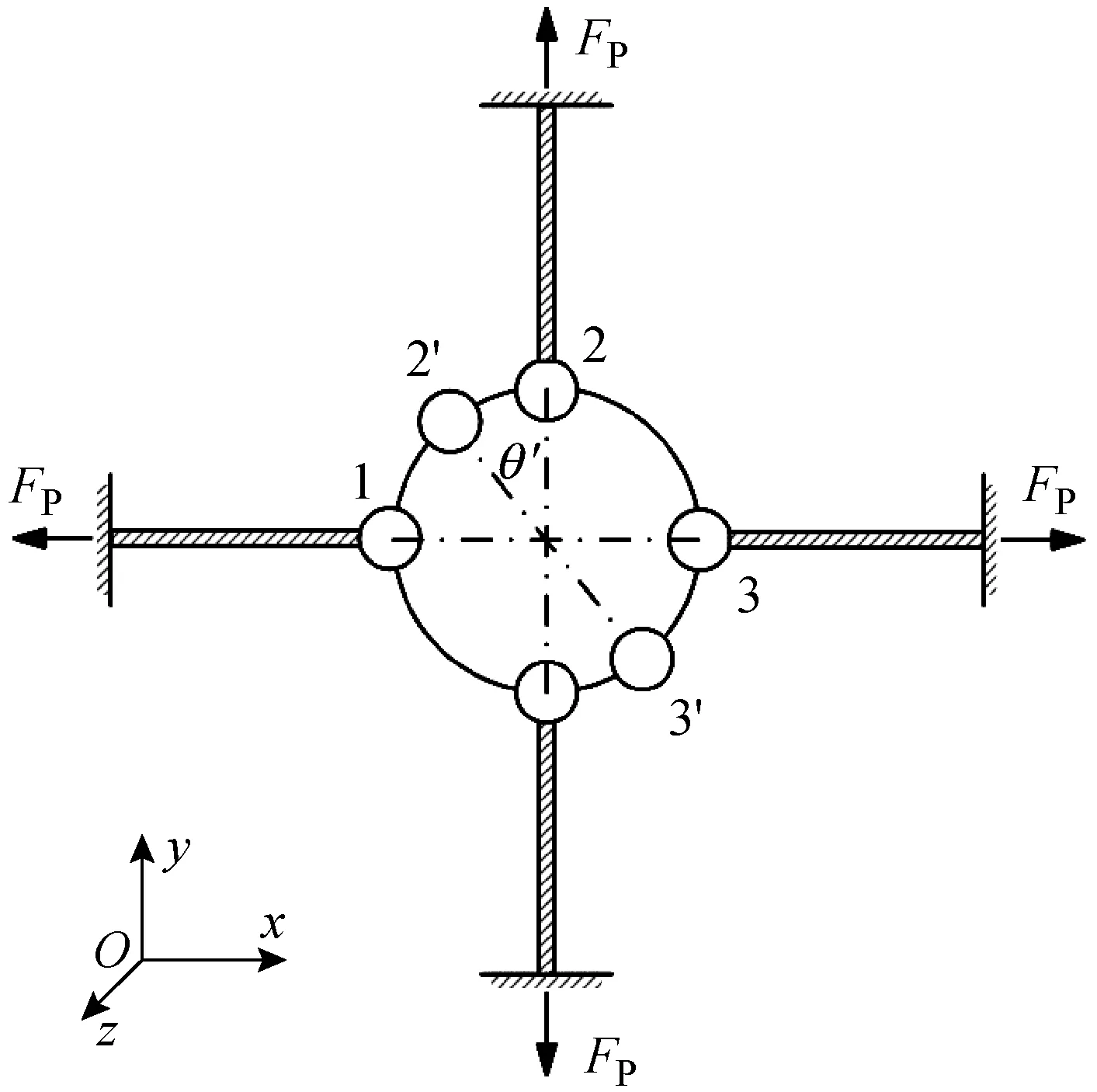
图10 艉支承子结构

3.1支承固有振动

支承剑被简化成欧拉-伯努利梁考虑，其横向振型函数[21]可以表示为

(1)

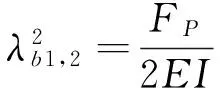
(2)

式中:Ab、Bb、Cb、Db为待定常数;Fp为纵向预紧力;ωb为横向振动固有频率;E,ρ分别为材料的弹性模量和密度;A为梁的截面面积;I为梁横截面惯性矩。

纵向振型函数[21]：

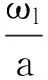
(3)

式中:Al、Bl为待定常数;ωl为纵向振动固有频率。

3.2协调条件和边界条件

协调条件包括位移协调条件和力平衡条件，其中，力平衡条件可以由位移协调条件推得。由于四个铰接点之间没有相对位移，故满足下列位移协调条件：

x′+Rb(1-cosθ′)=u1(x,t)|x=-Rb

(4a)

y′-Rbsinθ′=w1(x,t)|x=-Rb

(4b)

x′-Rbsinθ′=w2(y,t)|y=Rb

(4c)

y′-Rb(1-cosθ′)=-u2(y,t)|y=Rb

(4d)

x′-Rb(1-cosθ′)=-u3(x,t)|x=Rb

(4e)

y′+Rbsinθ′=-w3(x,t)|x=Rb

(4f)

x′+Rbsinθ′=-w4(y,t)|y=-Rb

(4g)

y′+Rb(1-cosθ′)=u4(y,t)|y=-Rb

(4h)

式中:ui、wi为i号支承剑的纵、横向振动位移，(x′,y′)是轴承套中心的坐标;Rb是轴承套半径。

以1号支承剑为例，其边界条件可以表示为

(5a)

u1(x,t)|x=-(Rb+l)=0

(5b)

式中，l为支承剑的长度。

式(1)、(3)中的常数可以通过条件式(4)、(5)确定，支承剑的横向和纵向固有振动频率及其模态即可确定。

轴承套中心位移可以表示如下：

x′(t)=[u1(-Rb,t)-u3(Rb,t)]/2

(6a)

y′(t)=[u4(-Rb,t)-u2(Rb,t)]/2

(6b)

θ′(t)=[w4(-Rb,t)+w2(Rb,t)]/(2Rb)

(6c)

3.3摩擦模型

轴颈-轴承接触界面的摩擦模型对分析结果起着决定性作用[22-23]。当转轴运转时，轴承-轴颈接触模型如图11所示。转轴与支承之间的摩擦激励可以等效为通过转轴轴心的摩擦力Ff和力矩Mf，两者都会诱导转轴及支承振动。为了模拟低速重载工况下水润滑橡胶轴承的摩擦特性，本文选用经典的速度依赖型Stribeck摩擦因数模型。

动摩擦因数μd可表示为

μd=a0sgn(vr)exp(b0(c0+|vr|)-1)Pd0

(7)

式中:a0、b0、c0、d0均是常数;vr为轴颈-轴承间的相对滑动速度;P为轴承比压;sgn(·)为符号函数。其中b0体现μd相对于vr的变化梯度。

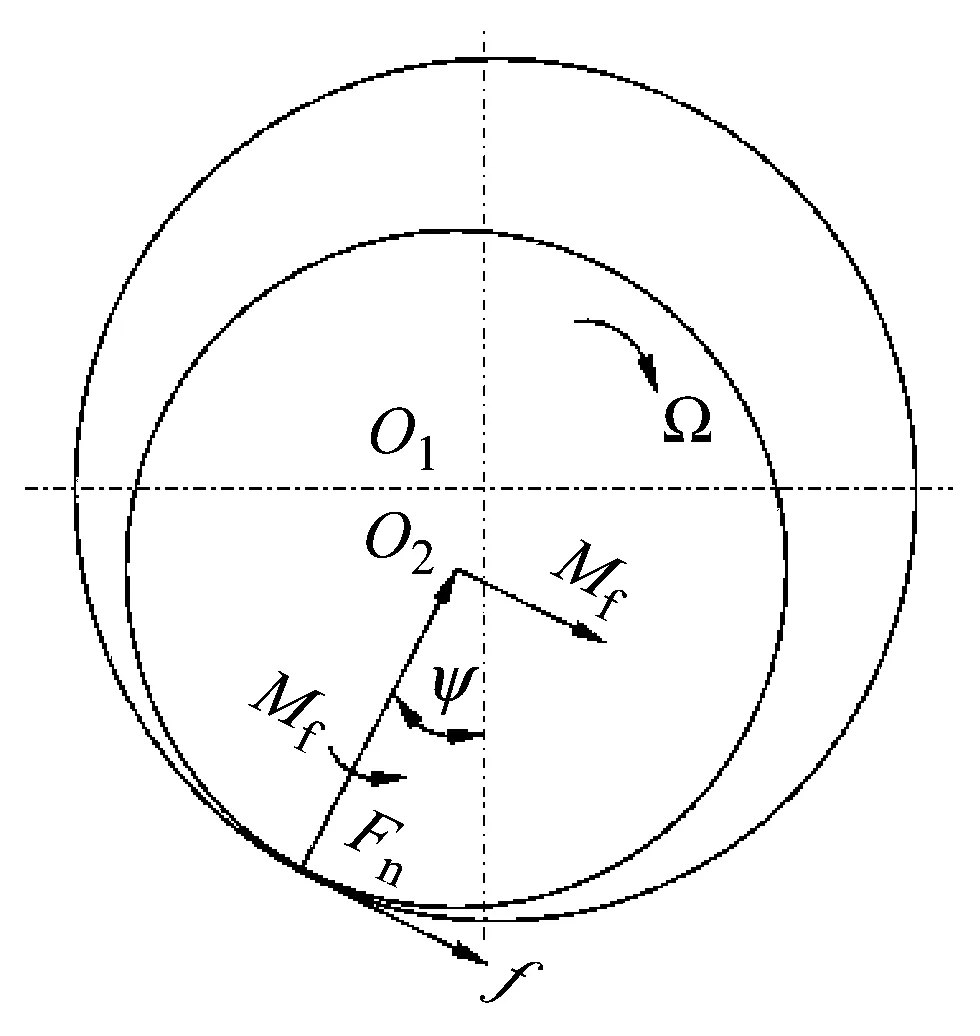
图11 轴颈-轴承接触模型

摩擦力Ff，力矩Mf：

Ff=FN·μd(vr),Mf=Ff·R

(8)

式中:FN为轴颈-轴承间的法向接触力;R为转轴截面半径。

轴颈-轴承间相对滑动速度的水平分量vrx：

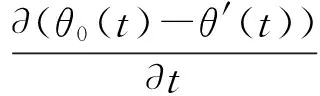
(9)

式中:Ω为转轴转速;θ0、x0分别为转轴扭转振动角位移和X方向横向振动位移。同理，可以表示出轴颈-轴承间相对滑动速度的竖直分量。

3.4系统耦合振动

转轴和支承之间通过轴承摩擦激励耦合，在轴承摩擦作用下，支承剑的纵向受迫振动表示如下：

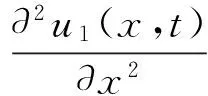
(10)

式中，FNx为轴颈-支承间水平方向接触力。

支承剑的横向受迫振动：

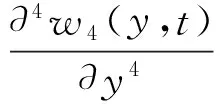
Ffxδ(y,t)|y=-Rb

(11)

式中，Ffx为轴颈-轴承间水平方向摩擦力。

利用模态叠加法[24]对上述方程进行降阶处理：

(12)

(13)

式中，Uir(x)、Wir(x)分别为i号支承剑的第r阶纵、横向振动模态向量，qiur(t)、qiwr(t)为相应的模态坐标。

将式(12)、(13)分别代入式(10)、(11)：

(14)

Ffxδ(y,t)|y=-Rb

(15)

利用模态向量正交性，在式(14)、(15)两边分别乘以U1j(x)和W4j(y)，并将方程写成矩阵形式：

(16)

(17)

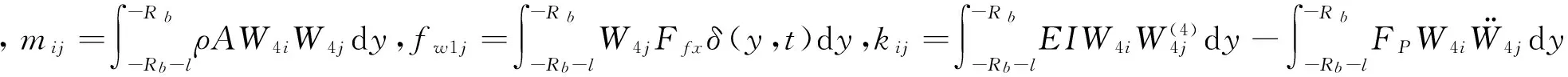
考虑水的质量效应，式(16)、(17)可以写成是式(18)、(19):

(18)

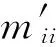
(19)

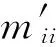
为了考虑结构的阻尼效应，本文采用式(20)的Rayleigh阻尼[21]：

C=αM+βK

(20)

式中，α和β是系数向量。

式(18)、(19)可分别写成：

Ku1qu1(t)=Fu1

(21)

Kw4qw4(t)=Fw4

(22)

本文主要考虑艉支承振动的影响，故将转轴简化成单自由度系统，其动力学方程如下：

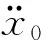
(23a)

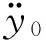
(23b)

(23c)

式中：ms为转轴质量；cx、cy分别为轴承水平、竖直方向阻尼系数;kx、ky分别为轴承水平、竖直方向刚度;Jsp为转轴极转动惯量;cθ为转轴扭振阻尼系数;kθ为转轴扭振刚度。上述参数取值均与转轴的某阶模态参数对应。Ffy为轴颈-支承之间竖直方向摩擦力。

4 数值仿真

4.1参数估计

为了估计部分振动模态阻尼比，测试艉支承的传递函数，其中，激励点和振动拾取点均位于水平支承剑，如图12所示。

测试结果如图13所示，其中包括转轴静止和转动两种状态下的频响函数。从图中可知，86.5 Hz和113.5 Hz所对应的模态受转轴转动的影响，频率发生偏移，相反，30.5 Hz和80 Hz多对应的模态则不受转轴转动的影响。比较测试和有限元计算结果，30.5 Hz、80 Hz、113.5 Hz为艉支承固有振动频率，86.5 Hz为转轴固有频率。113.5 Hz对应的模态阻尼比约为0.007，远小于其它模态阻尼比。

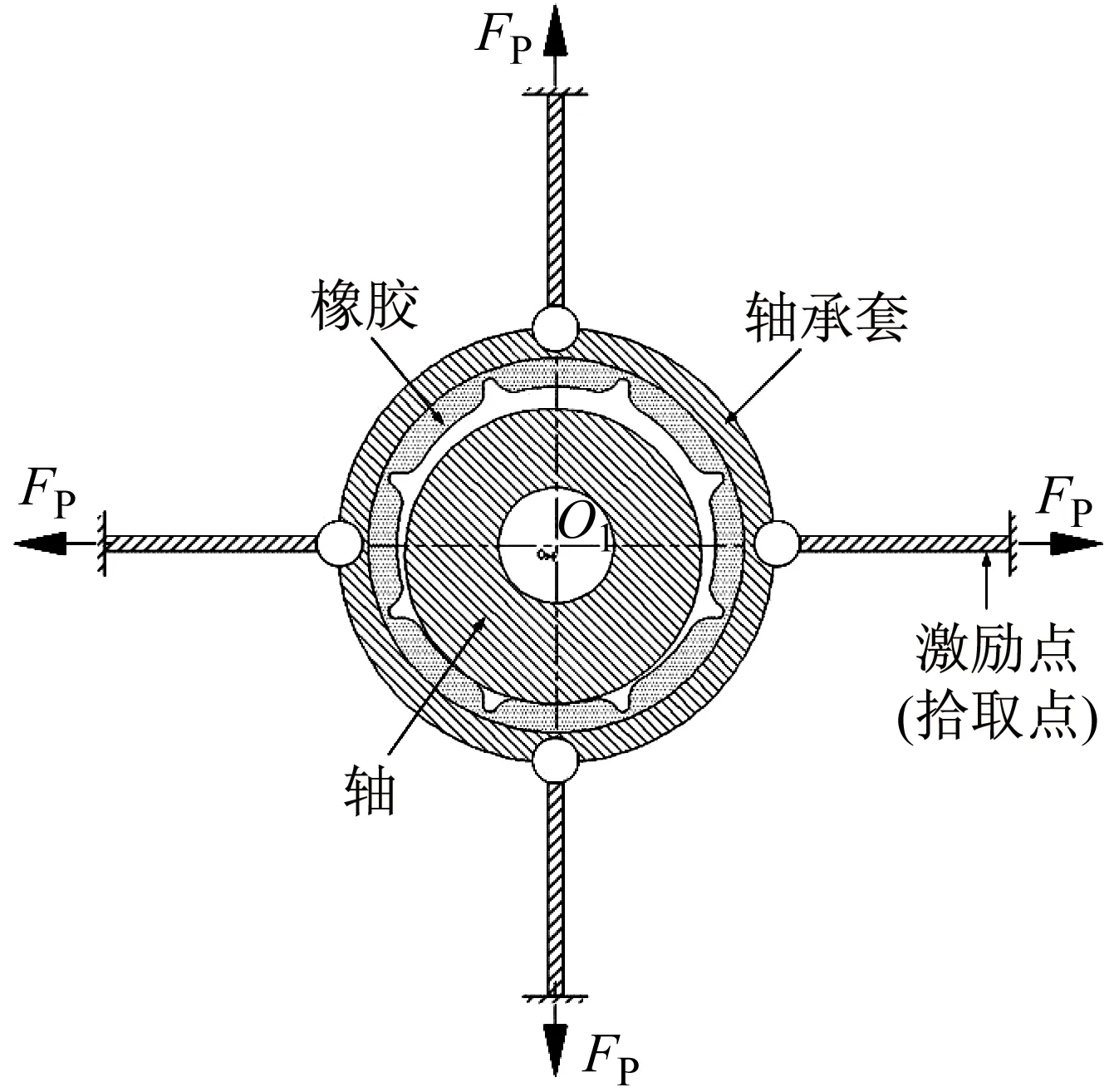
图12 测点布置示意图

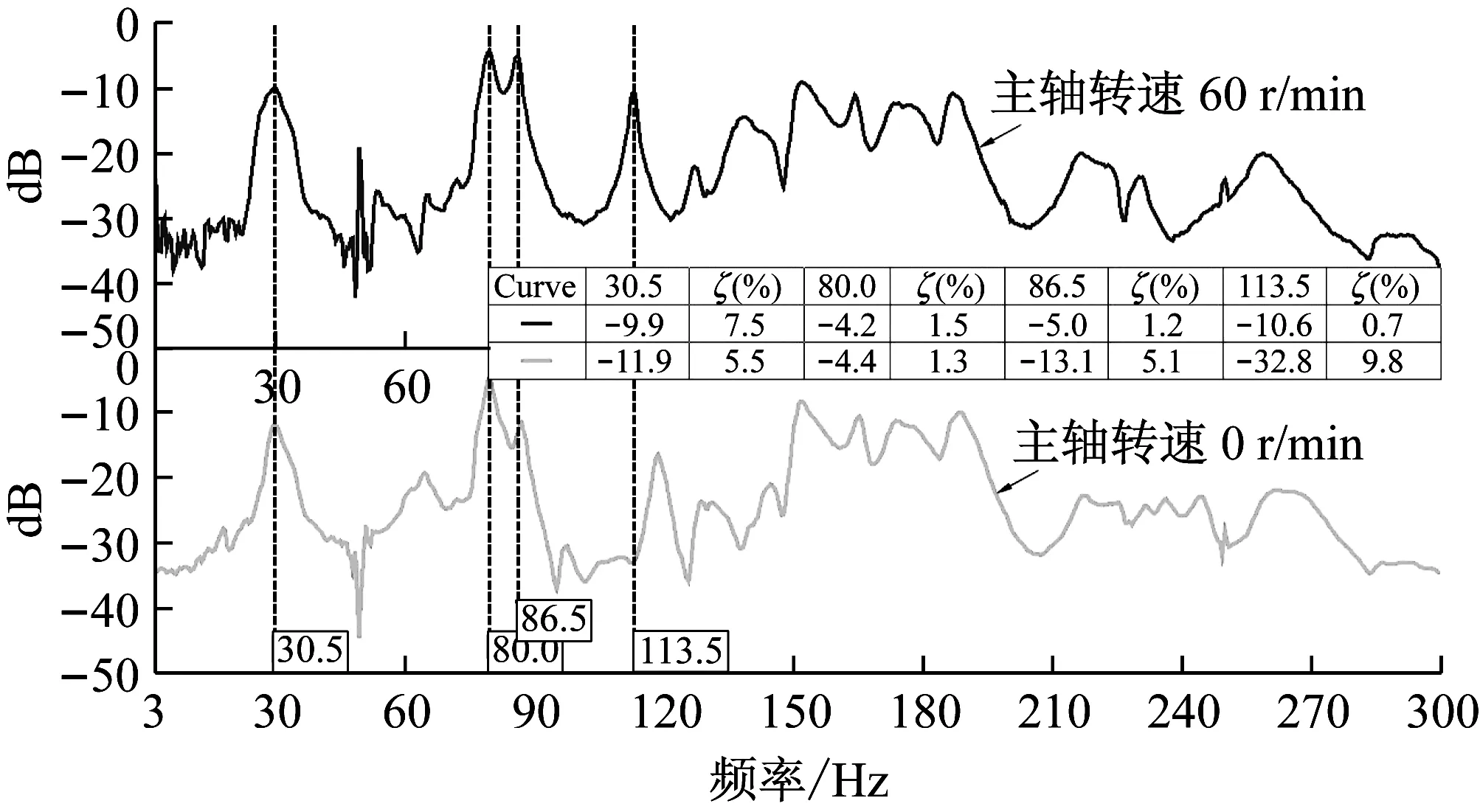
图13 艉支承传递函数

4.2动力响应分析

采用定步长四阶Runge-Kutta方法联立求解动力学方程式(21)、(22)、(23)，并分析轴承载荷、静摩擦系数、模态阻尼比、转轴转速以及β0等系统参数对响应特性的影响。在此仅列举以下几组参数：

(1) 所有模态阻尼比均为0.01，转轴转速60 r/min，a0=0.004 1，b0=4.042，c0=0.893 4，d0=-0.390 4，P=0.1 MPa；

(2) 艉支承第五阶模态阻尼比取0.007，其它模态阻尼比取0.02，转轴转速60 r/min，a0=0.004 1，b0=4.042，c0=0.893 4，d0=-0.390 4，P=0.1 MPa；

(3) 所有模态阻尼比均为0.01，转轴转速60 r/min，a0=0.004 1，b0=4.2，c0=0.893 4，d0=-0.390 4，P=0.1 MPa；

(4) 艉支承第五阶模态阻尼比取0.007，其它模态阻尼比取0.02，转轴转速60 r/min，a0=0.004 1，b0=4.2，c0=0.893 4，d0=-0.390 4，P=0.1 MPa；

(5) 艉支承第五阶模态阻尼比取0.007，其它模态阻尼比取0.02，转轴转速30 r/min，a0=0.004 1，b0=4.042，c0=0.893 4，d0=-0.390 4，P=0.1 MPa；

(6) 艉支承第五阶模态阻尼比取0.007，其它模态阻尼比取0.02，转轴转速90 r/min，a0=0.004 1，b0=4.042，c0=0.893 4，d0=-0.390 4，P=0.1 MPa；

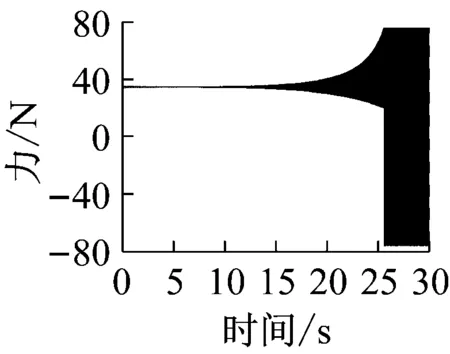
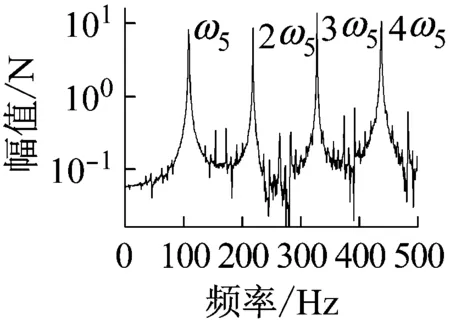
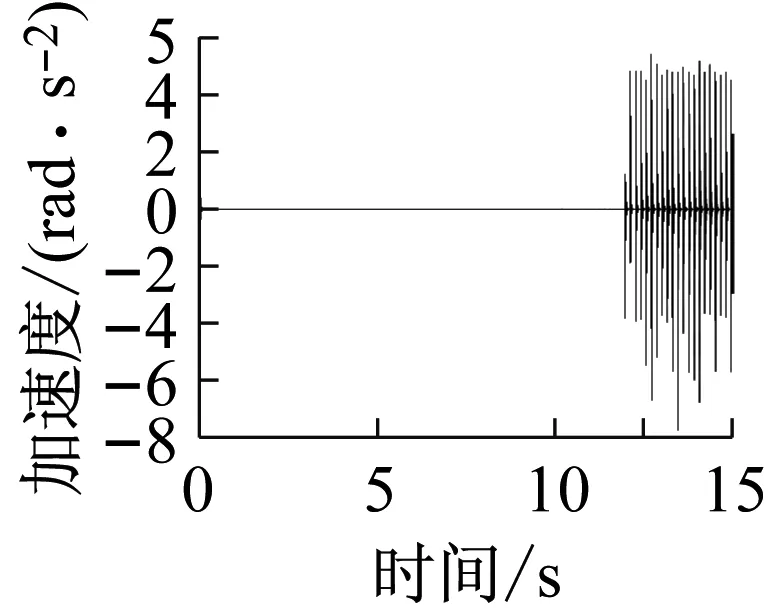
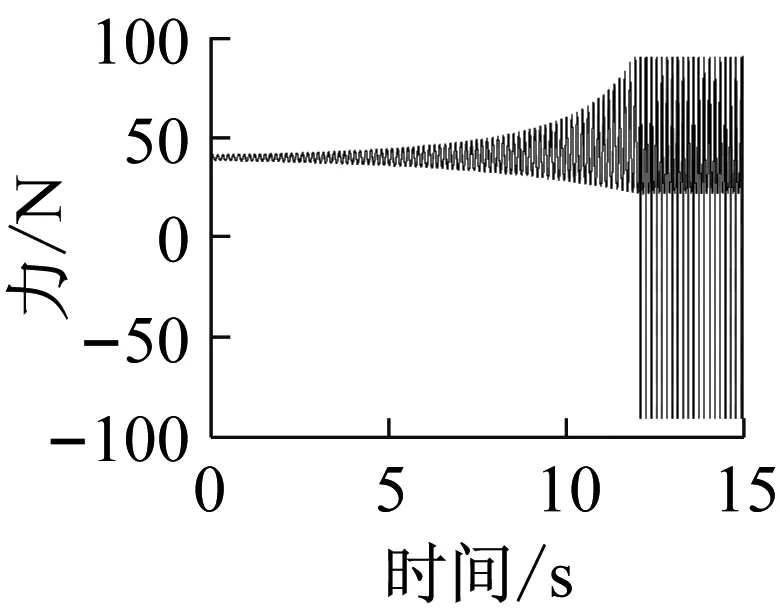
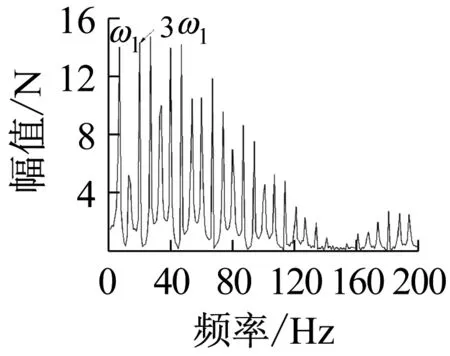
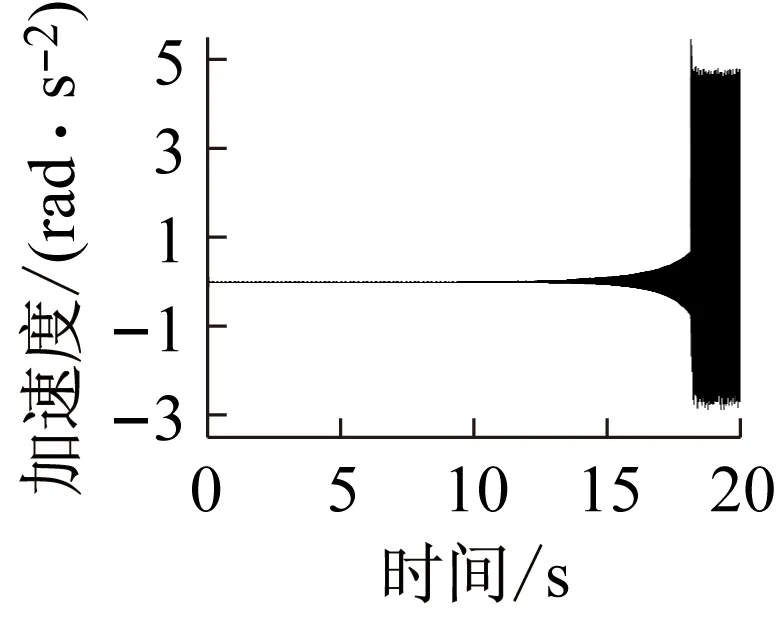
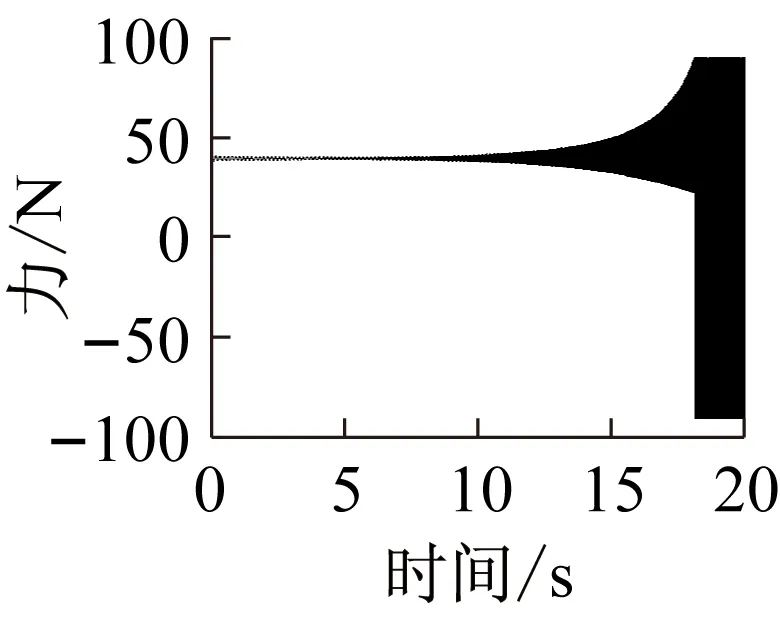
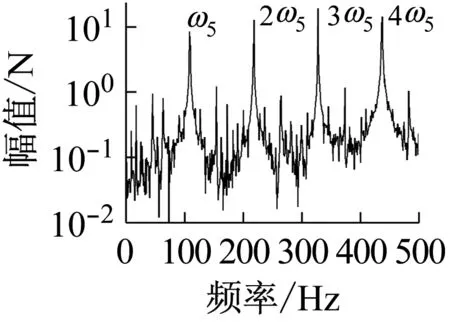
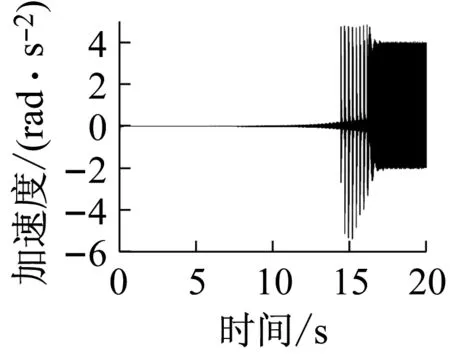
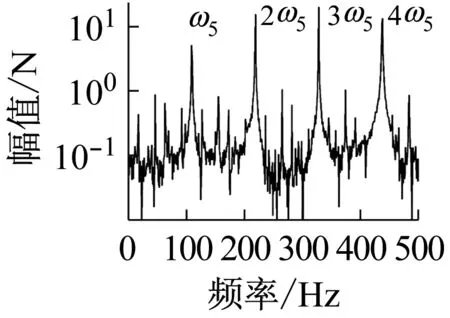
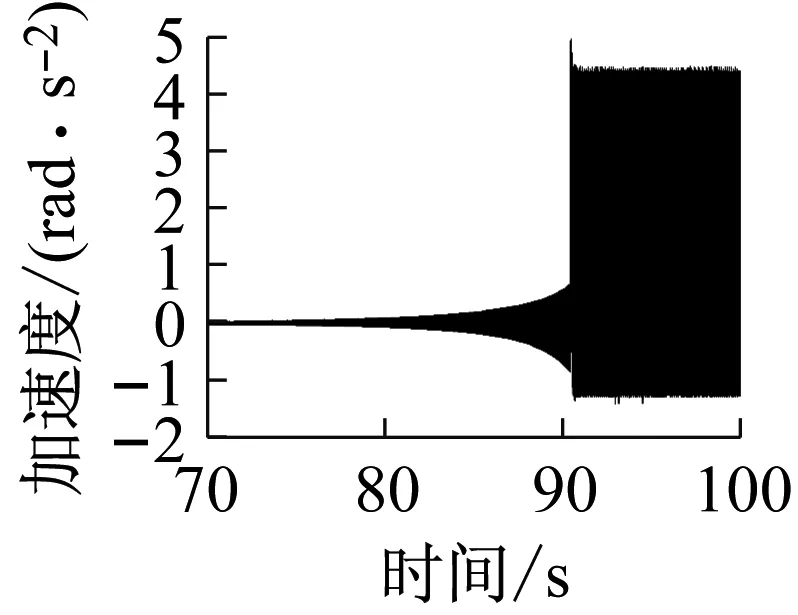
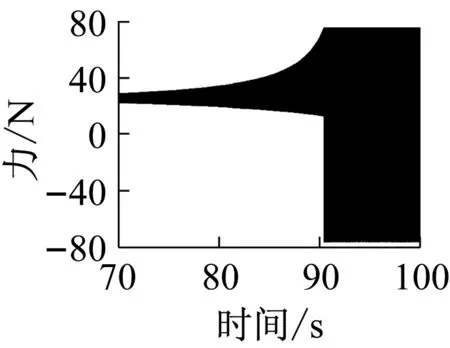
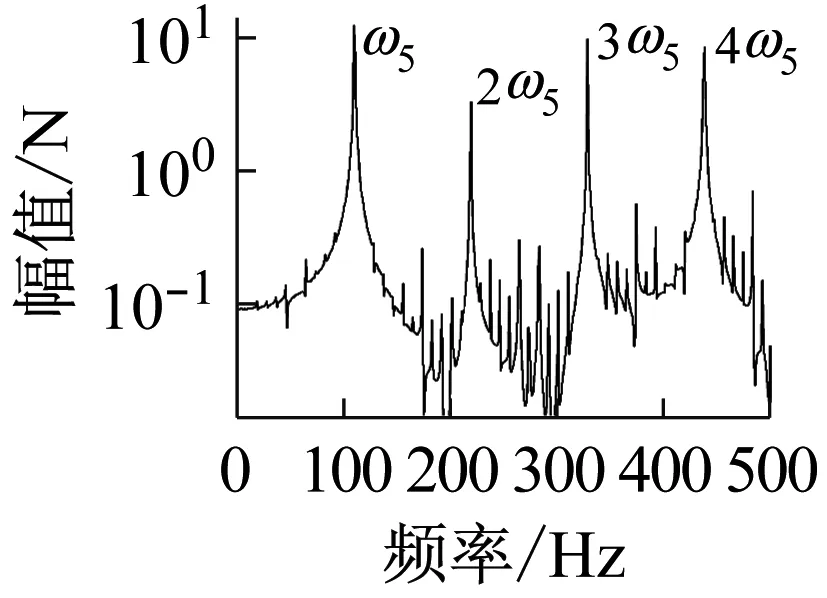
上述六组参数所对应的系统响应分别如图14～19所示，其中，14(a)、15(a)、16(a)、17(a)、18(a)、19(a)是转轴扭转振动加速度的时域响应特征；14(b)、15(b)、16(b)、17(b)、18(b)、19(b)为轴承界面水平方向摩擦力的时域特征；14(c)、15(c)、16(c)、17(c)、18(c)、19(c)为相应摩擦力的频域特征。

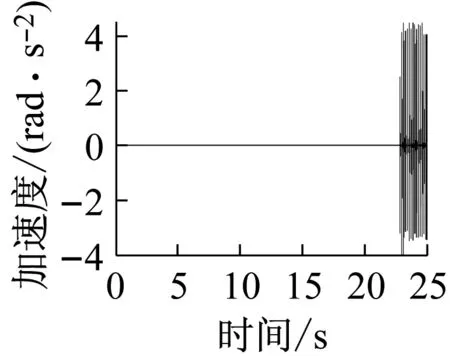
(a)

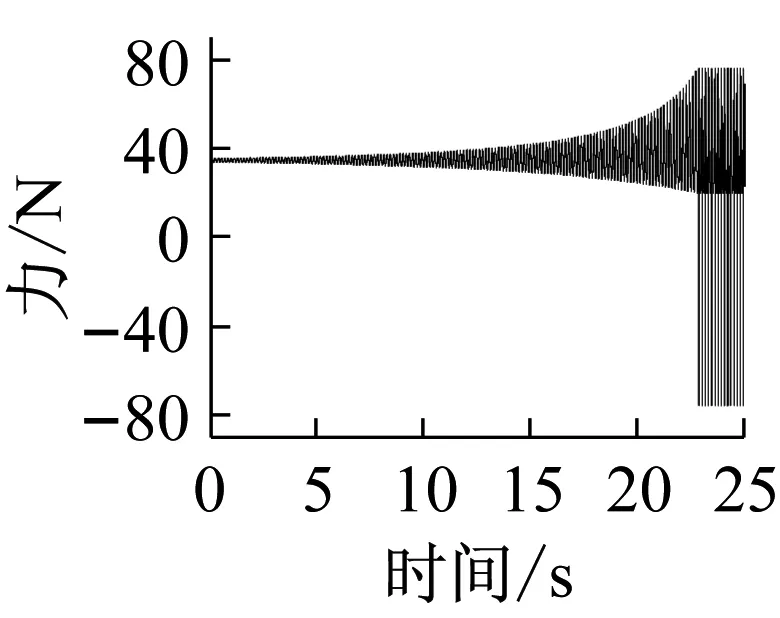
(b)

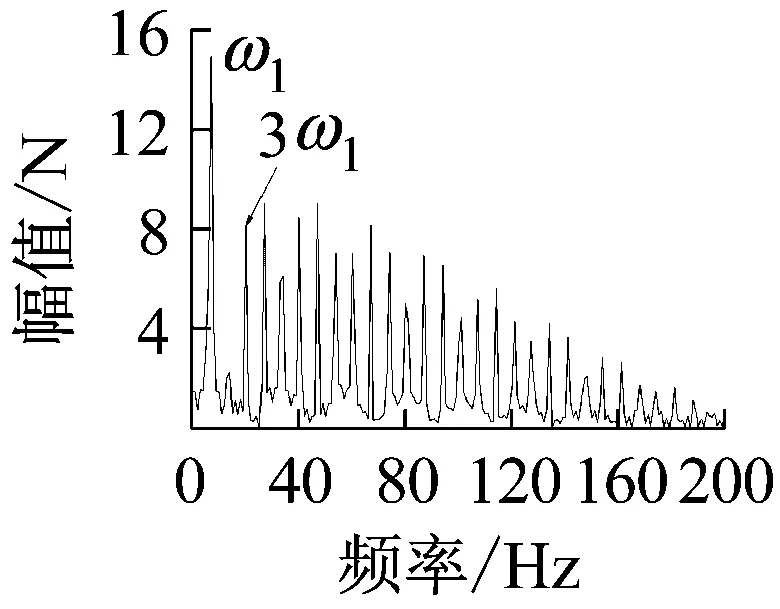
(c)

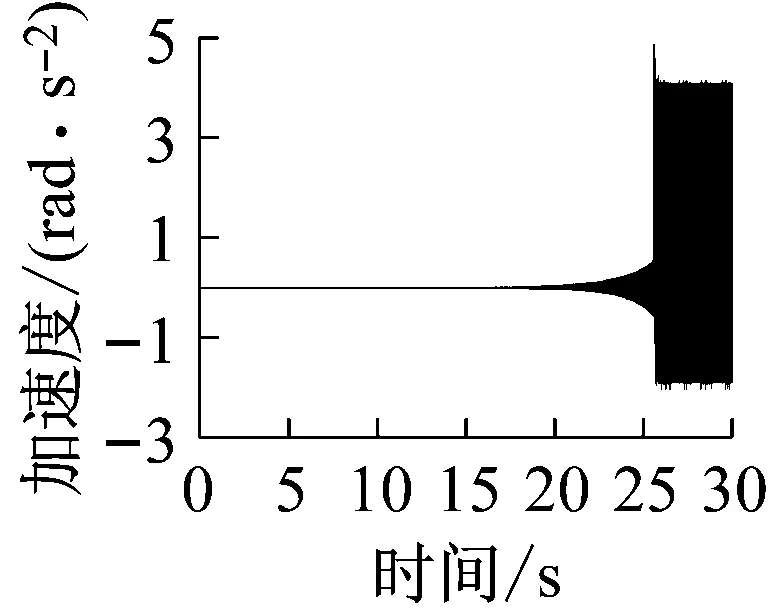
(a)

(b)

(c)

上述六组参数所对应的系统响应均有自激失稳现象产生，其中，图14(c)、16(c)所示失稳频率为艉支承的第一阶振动频率(ω1)，图15、17、18、19(c)所示失稳频率为艉支承的第五阶振动频率(ω5)，即113.6 Hz的失稳频率,这与实验结果一致；比较图14、16与图15、17、18、19，说明模态阻尼比是决定相应模态是否失稳的主要因素；比较图1、3和图2、4，发现动摩擦系数关于相对滑动速度的梯度越大，越容易诱导系统失稳；比较图17、18、19，转轴转速越低，越容易诱导系统失稳。

(a)

(b)

(c)

(a)

(b)

(c)

(a)

(b)

(c)

(a)

(b)

(c)

5 结 论

实验结果与数值分析结果比较一致，轴承界面摩擦与弹性支承振动的耦合是系统产生自激振动的主要原因，其中，失稳模态为艉支承第五阶模态，模态振型表现为扭转振动且其模态阻尼比较小，说明模态振型及其模态阻尼比的大小决定其是否失稳。橡胶轴承引起的异常振动和噪声并非一定是其本身直接产生，可能由于耦合作用引起轴系中其它部件振动异常，这为识别轴系异常振动和噪声提供借鉴。同时，分析发现水润滑橡胶轴承摩擦激励诱导产生的系统自激失稳出现在某一特定转速范围内，轴承载荷、轴承界面接触特性以及主轴转速等均是影响轴承摩擦的主要因素，这为改善轴承界面摩擦特性提供参考。

[1] ORNDORFF JR R L. Water-lubricated rubber bearings, history and new developments[J]. Naval Engineers Journal, 1985, 97(7):39-52.

[2] 陈之炎. 船舶推进轴系振动[M]. 上海：上海交通大学出版社, 1987.

[3] CARLTON J. Marine propellers and propulsion[M]. Butterworth-Heinemann, 2012.

[4] HIRANI H, VERMA M. Tribological study of elastomeric bearings for marine propeller shaft system[J]. Tribology International, 2009, 42(2):378-390.

[5] 杨令康. 船舶尾轴尾轴承间的润滑与碰摩特性研究[D]. 武汉：武汉理工大学, 2010.

[6] 张略. 水润滑复合橡胶尾轴承振鸣音机理分析及试验研究[D]. 武汉：武汉理工大学, 2013.

[7] 张振果，张志谊，王剑，等. 螺旋桨推进轴系摩擦自激扭转振动研究[J]. 振动与冲击, 2013,32(19):153-158.

ZHANG Zhenguo, ZHANG Zhiyi, WANG Jian, et al. Friction induced self-excited vibration in a propeller shaft system[J]. Journal of Vibration and Shock, 2013, 32(19):153-158.

[8] ZHANG Z G, CHEN F, HUA H X. Analysis of friction-induced vibration in a propeller-shaft system with consideration of bearing-shaft friction[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2014, 228(8):1311-1328.

[9] 王磊，俞强，刘义军. 水润滑橡胶轴承摩擦噪声特性分析及试验研究[J]. 武汉理工大学学报(交通科学与工程版), 2015,39(2):451-454.

WANG Lei, YU Qiang, LIU Yijun. Characteristic analysis and experimental study on friction-induced noise in warer-lubricated rubber bearings[J]. Journal of Wuhan University of Technology (Transportation Science &Engineering), 2015,39(2):451-454.

[10] KRAUTER A I. Generation of squeal/chatter in water-lubricated elastomeric bearings[J]. ASME J Lubric Technol, 1981, 103:406-412.

[11] SIMPSON T A, IBRAHIM R A. Nonlinear friction-induced vibration in water-lubricated bearings[J]. Journal of Vibration and Control, 1996, 2(1):87-113.

[12] ERIKSSON M, JACOBSON S. Friction behavior and squeal generation of disc brakes at low speeds[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2001, 215(12):1245-1256.

[13] 李方，帅长庚，何琳，等. 橡胶轴承耦合转子系统动力学研究[J]. 噪声与振动控制, 2011,31(3):37-41.

LI Fang, SHUAI Changgeng, HE Lin, et al. Dynamic analysis of rotor system coupled by rubber bearings[J]. Noise and Vibration Control, 2011,31(3):37-41.

[14] 张振果，张志谊，陈锋，等. 摩擦激励下螺旋桨推进轴系弯扭耦合振动研究[J]. 机械工程学报, 2013,49(6):74-80.

ZHANG Zhenguo, ZHANG Zhiyi, CHEN Feng, et al. Research on the coupling between torsional and lateral vibrations in propeller-shaft system with friction[J]. Journal of Mechanical Engineering, 2013,49(6):74-80.

[15] ZHANG Z G, ZHANG Z Y, HUANG X C, et al. Stability and transient dynamics of a propeller-shaft system as induced by nonlinear friction acting on bearing-shaft contact interface[J]. Journal of Sound and Vibration, 2014, 333(12):2608-2630.

[16] 邹丞，王家序，余江波，等. 橡胶层厚度和硬度对水润滑整体式轴承摩擦因数的影响[J]. 润滑与密封, 2006(2):40-41.

ZOU Cheng, WANG Jiaxu, YU Jiangbo, et al. Effect of thickness and hardness of rubber unerlayer on frictional coefficient of water-lubricated integer bearings[J]. Lubrication Engineering, 2006(2):40-41.

[17] 姚世卫，胡宗成，马斌，等. 橡胶轴承研究进展及在舰艇上的应用分析[J]. 舰船科学技术, 2008,27(增刊1):27-30.

YAO Shiwei, HU Zongcheng, MA Biu, et al. The new development of rubber bearing and its application in warships[J]. Journal of Ship Science and Technology, 2008, 27(Sup1):27-30.

[18] 王浩. 新型水润滑橡胶尾轴承试验研究[D]. 武汉：武汉理工大学, 2012.

[19] 段海涛，吴伊敏，王学美，等. 新型水润滑轴承材料的摩擦学性能研究[J]. 武汉理工大学学报, 2012, 34(6):17-21.

DUAN Haitao, WU Yimin, WANG Xuemei, et al. Study on the tribological properties of new water-lubricated bearing materials[J]. Journal of Wuhan University of Technology, 2012, 34(6):17-21.

[21] RAO S S, YAP F F. Mechanical vibrations[M]. New York: Addison-Wesley, 1995.

[22] KALIN M, VELKAVRH I, VIZINTIN J. The Stribeck curve and lubrication design for non-fully wetted surfaces[C]. The 17th international conference in wear of materials, Las Vegas, Nevada, 2009.

[23] BERGER E J. Friction modeling for dynamic system simulation[J]. Applied Mechanics Reviews, 2002, 55(6): 535-577.

[24] 傅志方，华宏星. 模态分析理论与应用[M]. 上海:上海交通大学出版社, 2000.

Self-excitedvibrationofaflexiblysupportedshaftingsystemunderbearingfriction

QIN Wenyuan1,2, QIN Hui1,2, ZHENG Hongbo1,2, ZHANG Zhenguo1,2, ZHANG Zhiyi1,2

(1. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240；2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240)

Self-excited vibration characteristics and its mechanism of a flexibly supported shafting system placed in a gravity water tunnel and excited by a friction force from water-lubricated rubber bearings were investigated. Test results indicated that the system’s self-excited vibration appears at a specific rotating speed and remains unchanged with decrease in the shaft rotating speed, it disappears at a lower rotating speed due to inadequate driving force; the system’s self-excited vibration under a certain rotating speed reveals a single mode to be unstable under rotating speed modulation. To study self-excited vibration mechanism, the dynamic model of the system was built. In modeling, the system was divided into two substructures including a flexible support and a shaft to get their natural frequencies and modal shapes, respectively. According to compatible conditions and boundary conditions, a support-shaft coupled dynamic model under the action of a friction force on bearing interface was built, the mode superposition method was adopted to reduce orders of the model. The fourth order Runge-Kutta method was used to numerically solve the dynamic equations. The influences of the main physical parameters on the system’s vibration instability were analyzed. The test results agreed well with those of simulation. The results showed that the unstable mode is the support’s weakly damped torsional vibration one; the interaction between support vibration and bearing friction force is the main reason to cause the system unstable.

flexible support; friction excitation; coupled vibration; self-excited vibration

国家自然科学基金(51505281；11172166)

2016-04-18 修改稿收到日期：2016-06-23

覃文源 男，博士生，1986年7月生

张志谊 男，博士，研究员，博士生导师，1970年11月生 E-mail：chychang@sjtu.edu.cn

O323；TB53

： A

10.13465/j.cnki.jvs.2017.17.028