局部均值分解和排列熵在行星齿轮箱故障诊断中的应用

丁 闯, 张兵志, 冯辅周, 江鹏程

(装甲兵工程学院 机械工程系，北京 100072)

局部均值分解和排列熵在行星齿轮箱故障诊断中的应用

丁 闯, 张兵志, 冯辅周, 江鹏程

(装甲兵工程学院 机械工程系，北京 100072)

目前行星齿轮箱已经在军用和民用装备中广泛应用，研究行星齿轮箱的故障诊断方法意义重大。针对行星齿轮箱在运行时产生的非线性非平稳振动，且故障特征信号微弱等问题，提出一种结合局部均值分解和排列熵的行星齿轮箱故障诊断方法。利用局部均值分解方法将不同状态下的振动信号分解为多个乘积函数分量，针对包含有故障信息的分量进行排列熵计算，以此判断故障类型。最后通过采集行星齿轮箱故障模拟试验台三种状态(齿轮正常、太阳轮裂纹故障及行星轮裂纹故障)的振动信号，对其进行局部均值分解和排列熵计算，验证了此方法的有效性。

行星齿轮箱；LMD；排列熵；故障诊断

由于行星传动具有重量轻、体积小、传动比大、承载能力强、传动效率高等诸多优点，因此已被广泛应用于作战飞机、舰船、装甲车辆、自行火炮及风力发电和工程机械等军用装备和民用装备中[1]。由于行星齿轮箱结构复杂，不仅承受重载负荷，且运行工况复杂多变，在实际使用过程中，齿轮箱中的太阳轮、行星轮和齿圈、行星架等关键部件容易出现故障[2]。例如，我国某型主战坦克使用的多档位行星变速箱，共有三个行星排，结构非常复杂，使用条件异常恶劣，变速箱在使用过程中经常出现齿轮严重磨损、裂纹、断齿等机械故障，如果故障不能及时被发现并排除，将严重影响主战坦克的机动性能，导致战斗力下降，并造成变速箱的二次损伤，使维修费用大幅提高。

目前，国内外学者对定轴齿轮箱故障诊断进行了深入的研究，提出了一系列卓有成效的诊断方法，取得了丰硕的成果。然而行星齿轮箱的结构不同于定轴齿轮箱，一般由太阳轮、多个行星轮、齿圈、行星架等组成，通常齿圈固定，太阳轮绕中心轴旋转，而行星轮不仅绕各自中心轴自转，同时绕太阳轮中心轴公转，行星排结构如图1所示，行星齿轮箱的复杂结构决定了其振动响应比定轴齿轮箱更加复杂，并存在明显的非线性、非平稳性，且故障响应微弱。目前对于行星齿轮箱的故障诊断研究较少，应用尚不成熟。

近年来，排列熵算法的发展为行星齿轮箱的故障诊断提供了思路。行星齿轮箱在不同状态运行时，其振动规律将发生变化，而排列熵算法可准确计算这一变化。为了定量描述行星齿轮箱不同运行状态时振动规律的变化并识别其故障，本文提出一种结合局部均值分解(Local Mean Decomposition，LMD)和排列熵(Permutation Entropy，PE)的行星齿轮箱故障诊断方法。首先利用LMD方法分解行星齿轮箱的振动信号得到多个乘积函数分量(Product Function，PF)，并通过傅里叶变换求出每个PF分量包含的频率成分，找出含有故障信息的PF分量，然后计算此分量的排列熵，通过得到的排列熵值判断行星齿轮箱的工作状态和故障类型[3-4]，基于LMD和排列熵的行星齿轮箱故障诊断流程如图2所示。本文通过对齿轮正常、太阳轮裂纹及行星轮裂纹三种状态的振动信号进行分析说明了此方法的有效性。

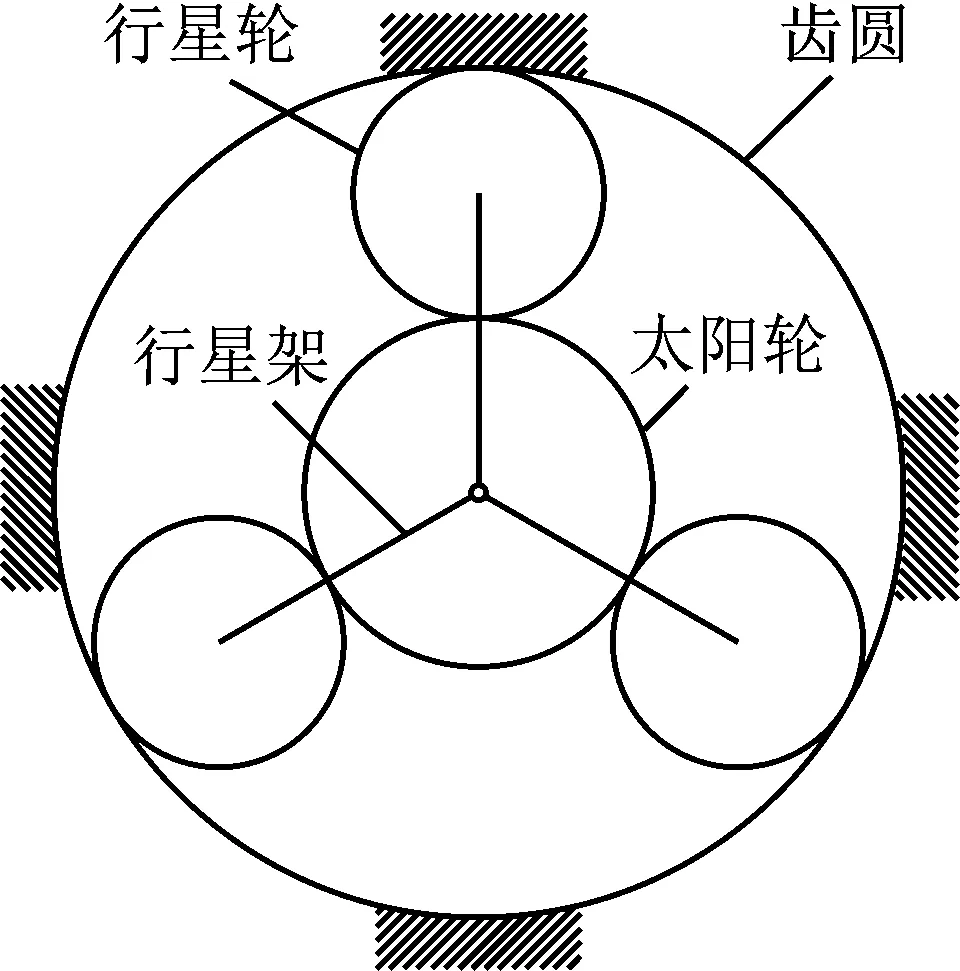
图1 行星排结构

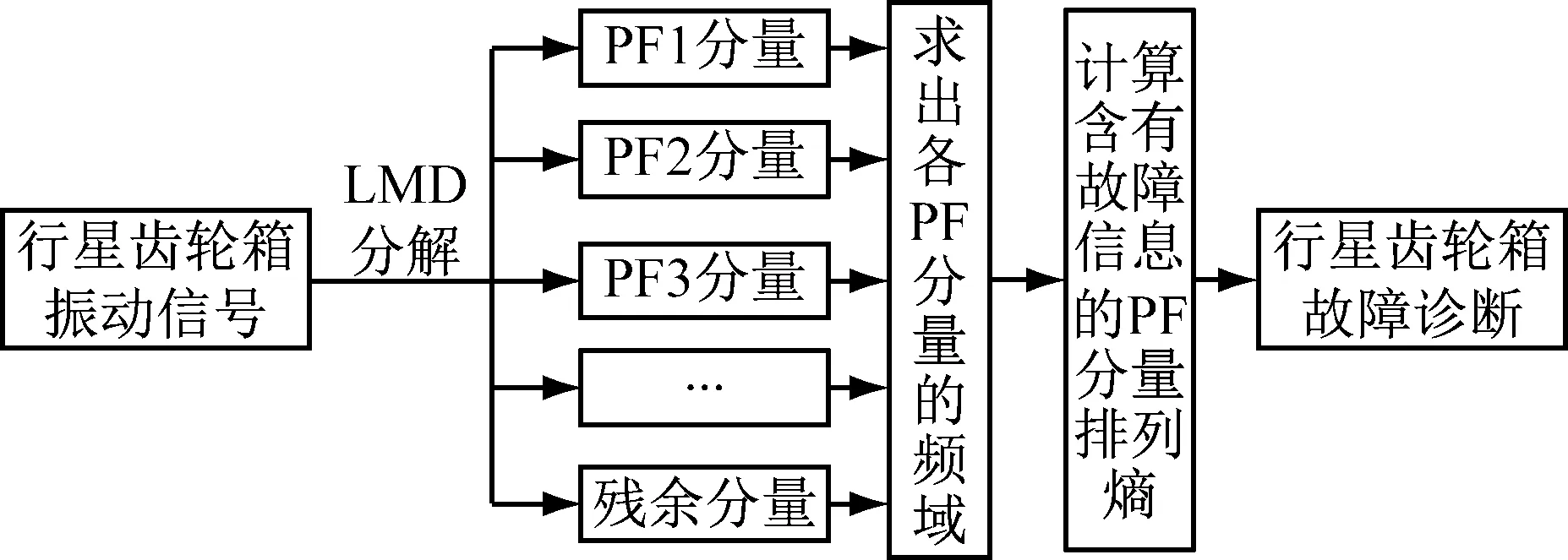
图2 LMD和排列熵故障诊断流程图

1 LMD原理

局部均值分解能自适应地将一个复杂信号分解成若干个瞬时频率具有物理意义的PF分量之和，且非常适合非线性和非平稳信号[5]。LMD方法能够克服小波分析及EMD存在的不足，且计算过程简单，迭代次数少。而小波分析因小波基有限存在能量泄漏，EMD存在模式混淆、端点效应等问题，这些问题的存在都将造成的分析结果不准确。

LMD得到的每一个分量由一个包络信号和一个纯调频信号相乘得到，包络信号即为该PF分量的瞬时幅值，而该PF分量的瞬时频率可由纯调频信号直接求出，LMD方法的计算流程如图3所示，详细分解过程见参考文献[6]。

2 排列熵算法

“熵”的概念最早被Shannon用于描述信息论中信息的不确定性，同时给出了信息熵的数学表达式，定义一个不确定的概率分布的信息熵为

(1)

式(1)中k为常数，信息熵的大小可定量描述概率系统的平均不确定程度。根据这一理论，最不确定的概率分布具有最大的熵值，即反映了信息其概率分布的均匀性。

根据信息熵理论的定义，Bandt等[7-9]提出了排列熵的概念，排列熵是用于衡量一维时间序列复杂度的平均熵参数，其对信号变化具有很高的敏感性，能够有效放大系统的微变信号，同时可以很好地检测出复杂系统的动力学突变，且该方法具有计算过程简单、抗噪声能力强等特点，因此排列熵对于非线性、非平稳性的振动信号具有很好的检测效果。由于排列熵自身的诸多优点使其在气象预测、医学等领域取得了广泛的应用，也逐渐扩展至了机械故障诊断方面[10-11]。

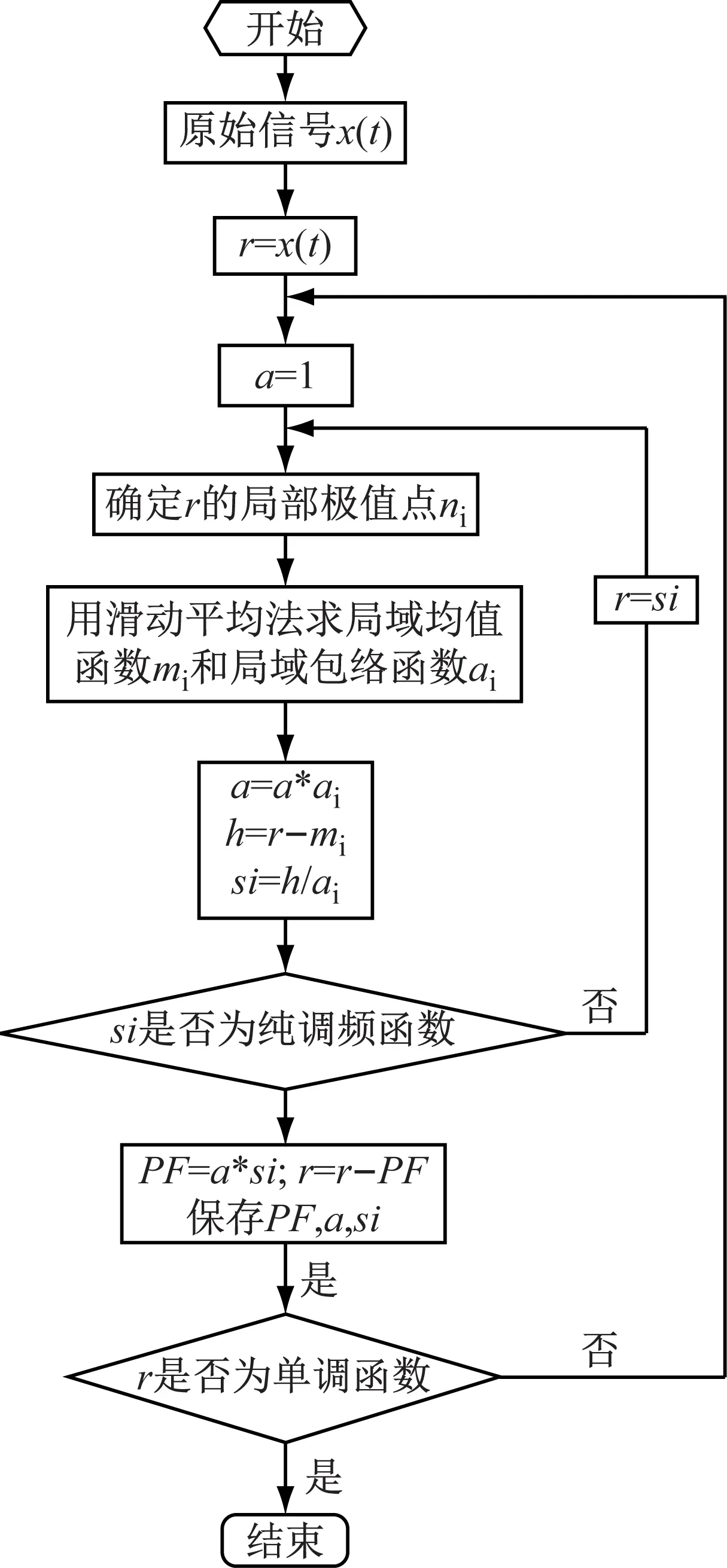
图3 LMD方法的计算流程

排列熵的基本原理如下：

(1)相空间重构

假设有一时间序列X={x(i),i=1,2,3,…,n}，对此序列进行相空间重构，得到重构矩阵Y：

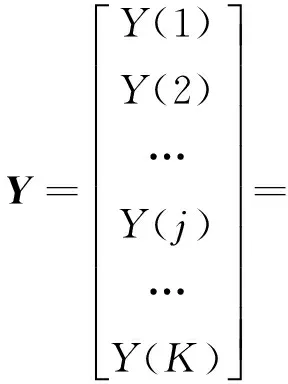
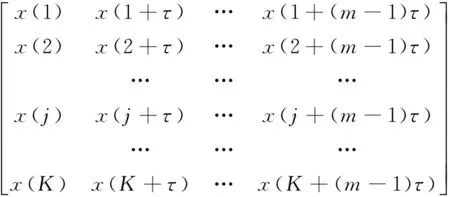
(2)

式中：j=1,2,3,…,K,m为嵌入维数，τ为延迟时间，K+(m-1)τ=n。重构矩阵中的每一行Y(j)为一个重构分量，重构矩阵中共有K个重构分量。

(2)升序排列

将重构矩阵Y中的第j个重构分量Y(j)={x(j)x(j+τ) …x(j+(m-1)τ)}按照升序重新排列，i1i2…im表示重构分量中各个元素所在列的位置索引，即:

x(j+(i1-1)τ)≤x(j+(i2-1)τ)≤…≤

x(j+(im-1)τ)

(3)

若重构分量中存在相等的值，即

x(j-(ip-1)τ)=x(j-(iq-1)τ)

(4)

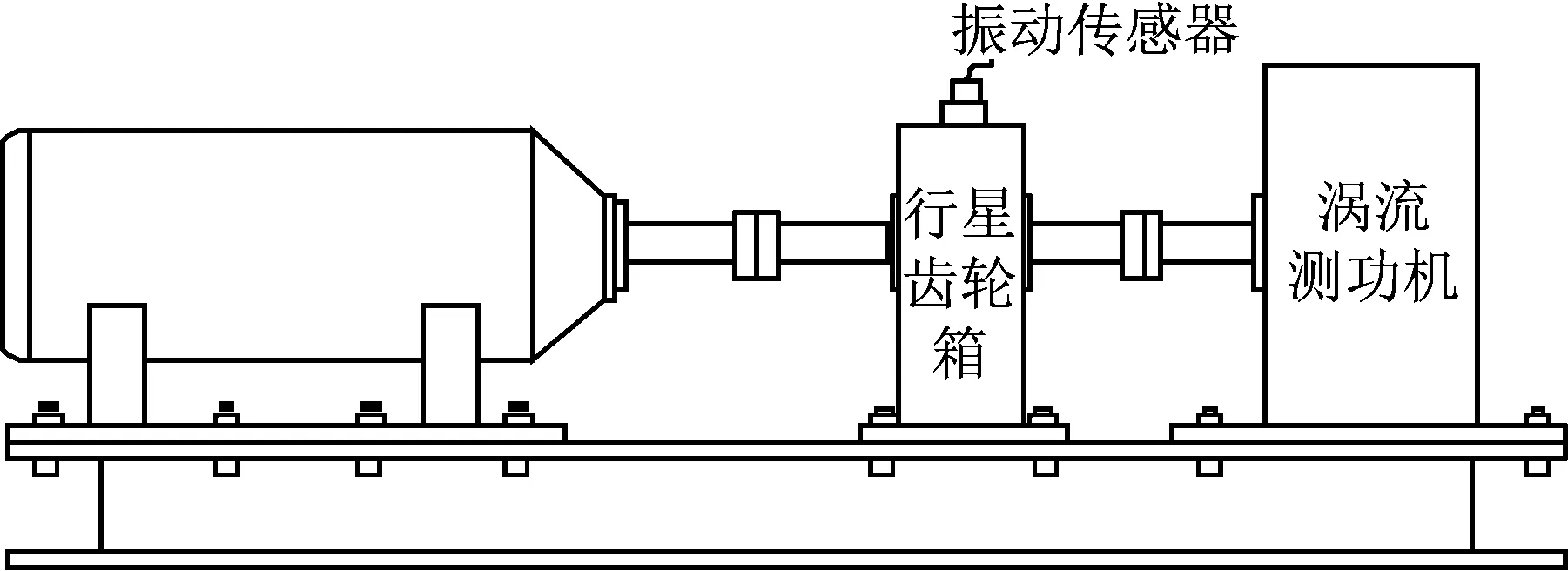
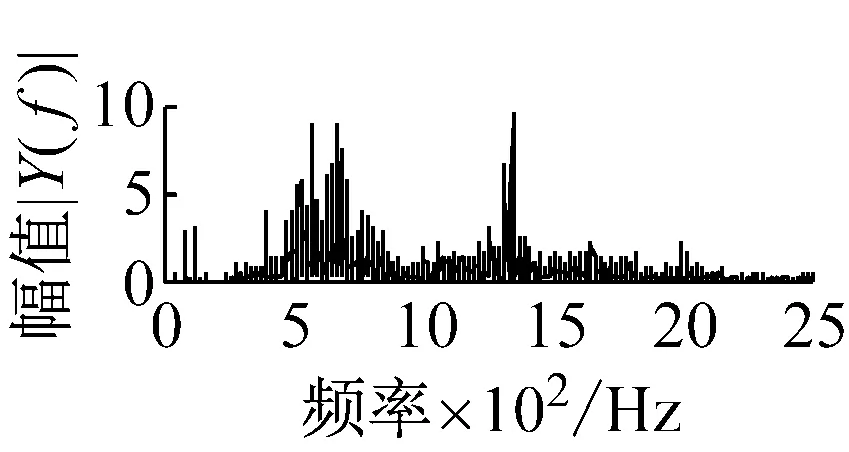
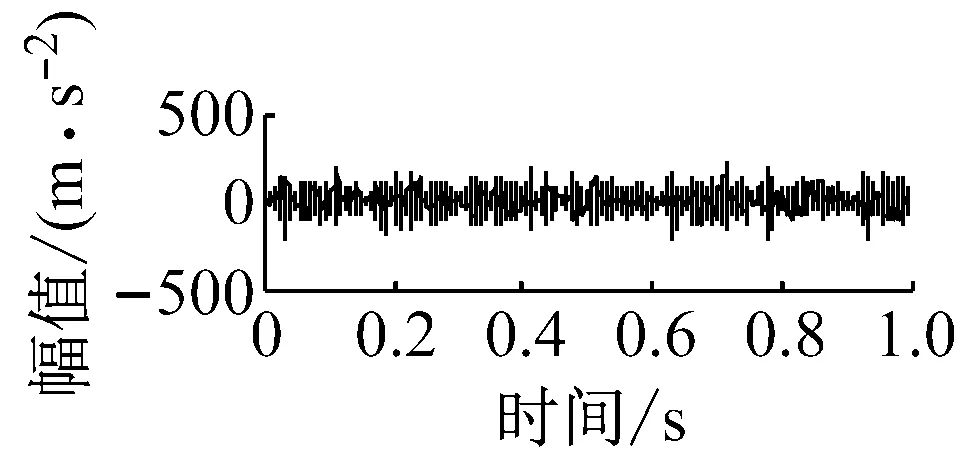
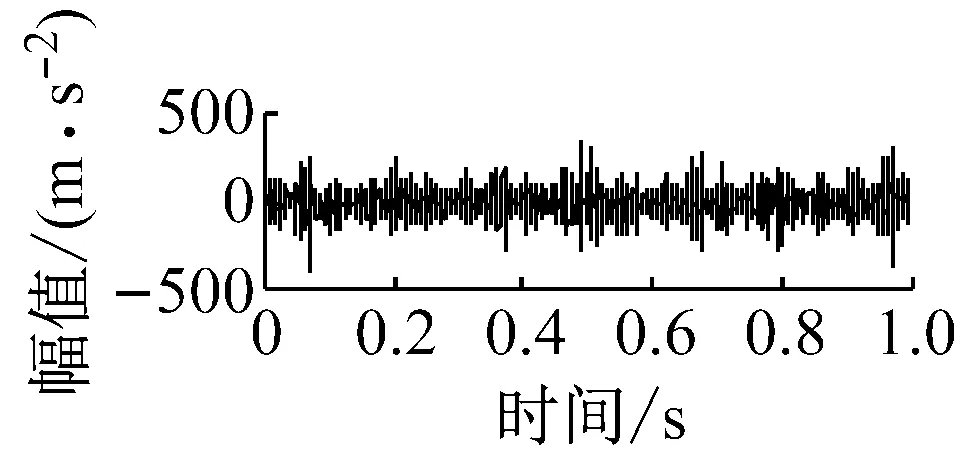
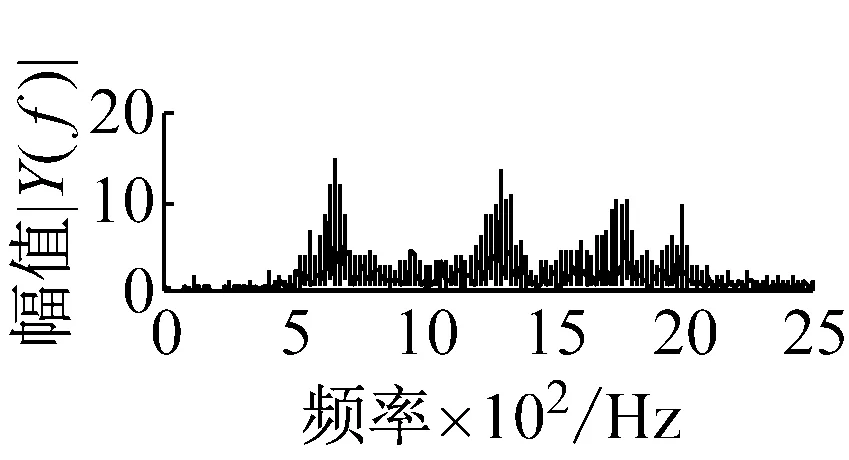
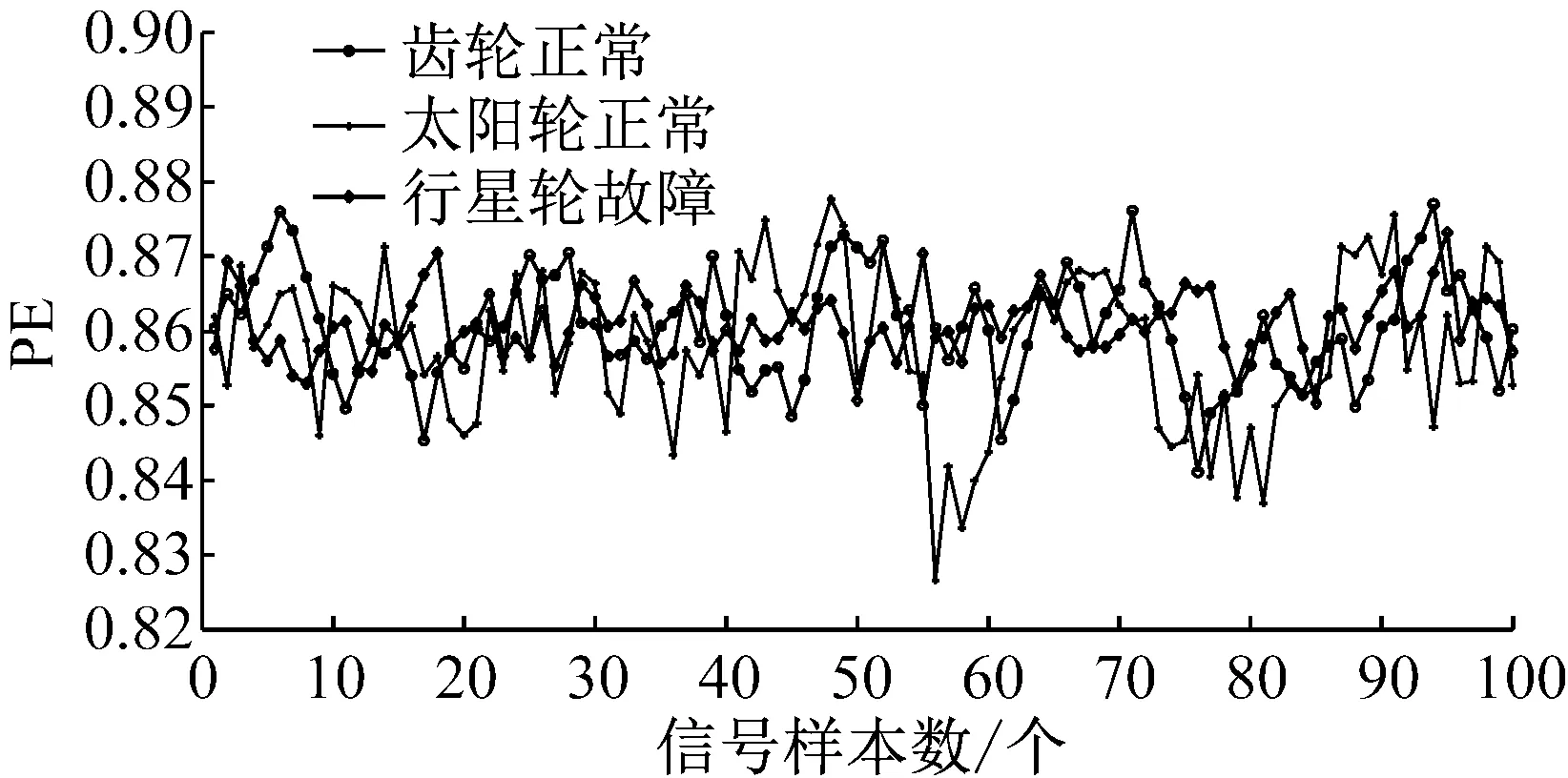
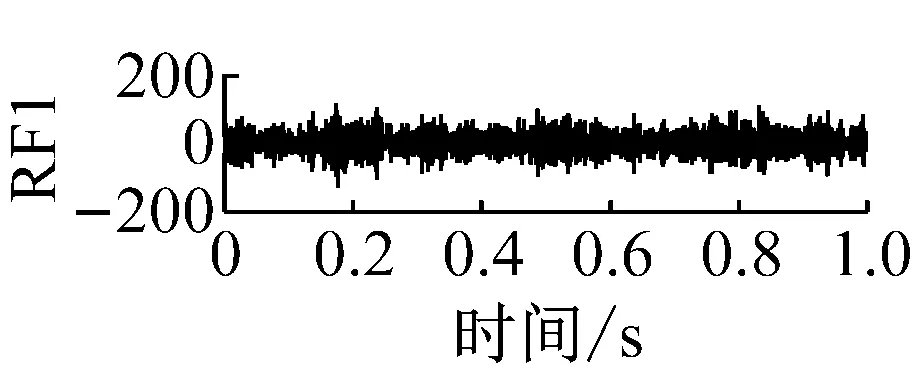
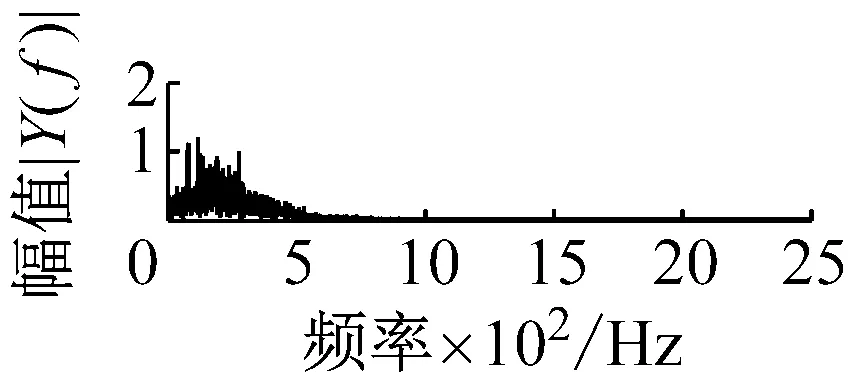
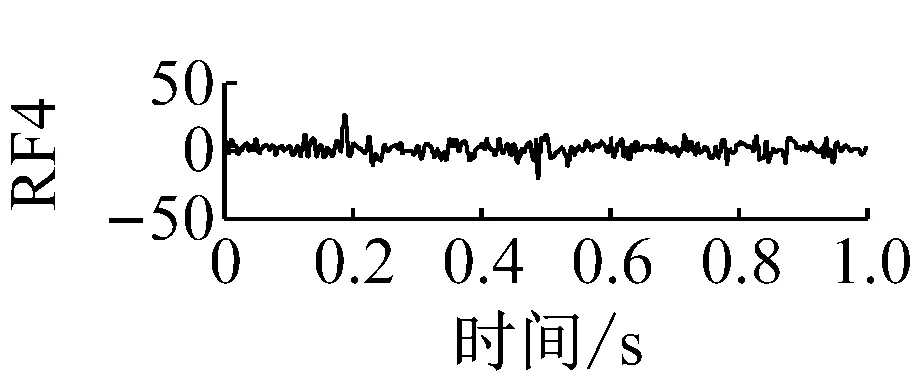
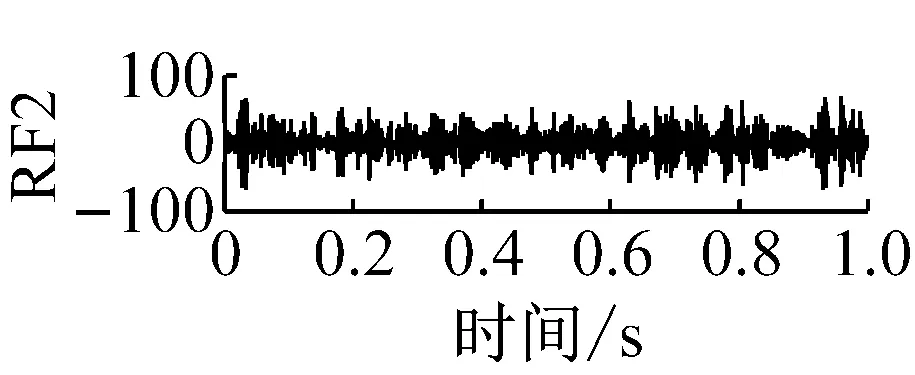
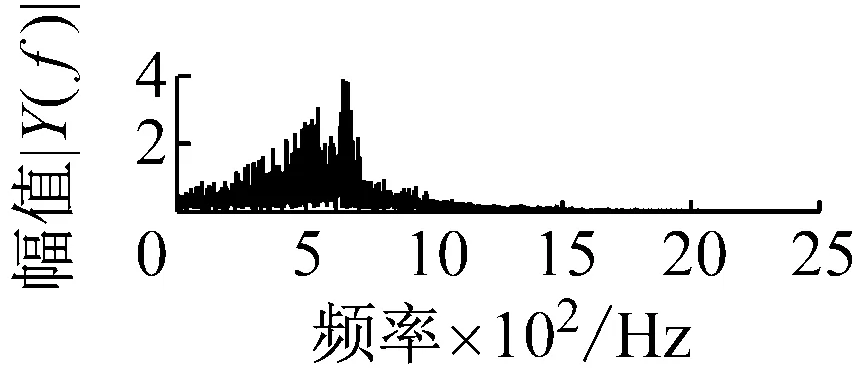
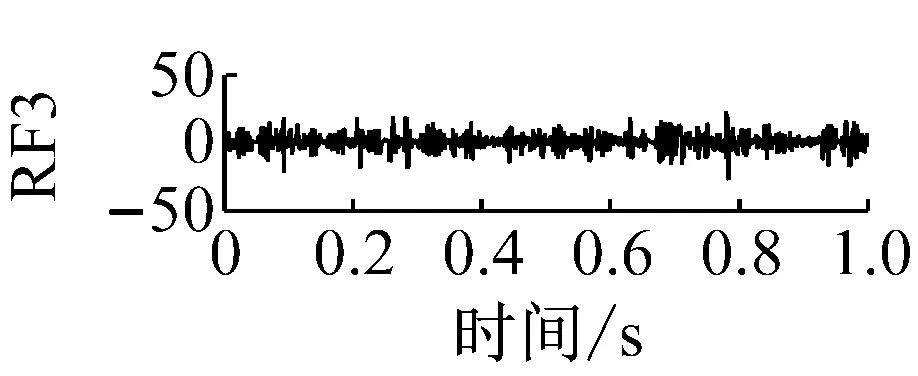
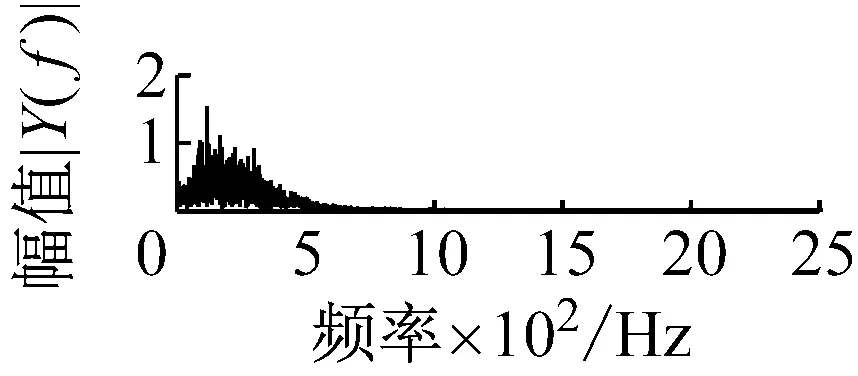
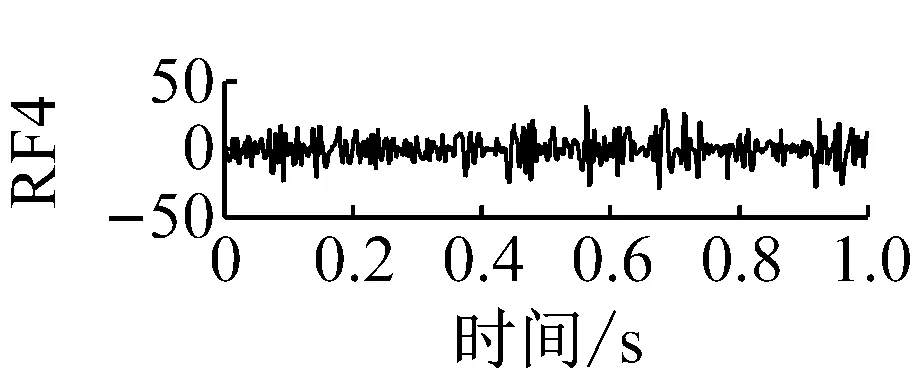
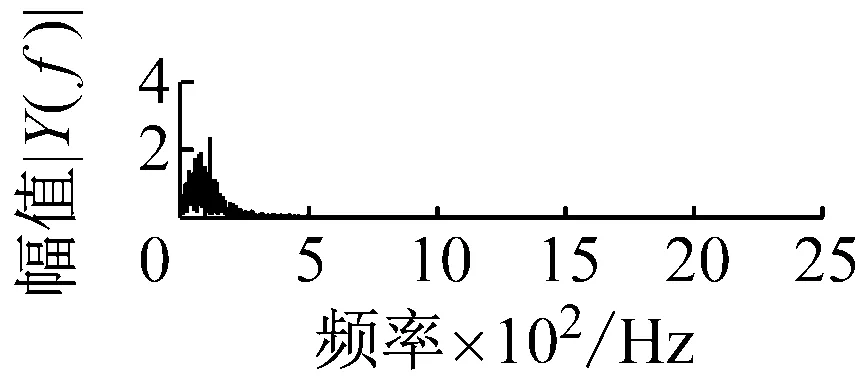
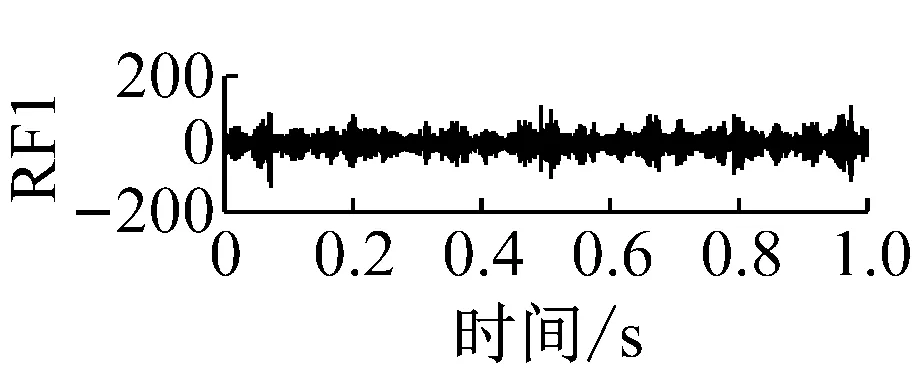
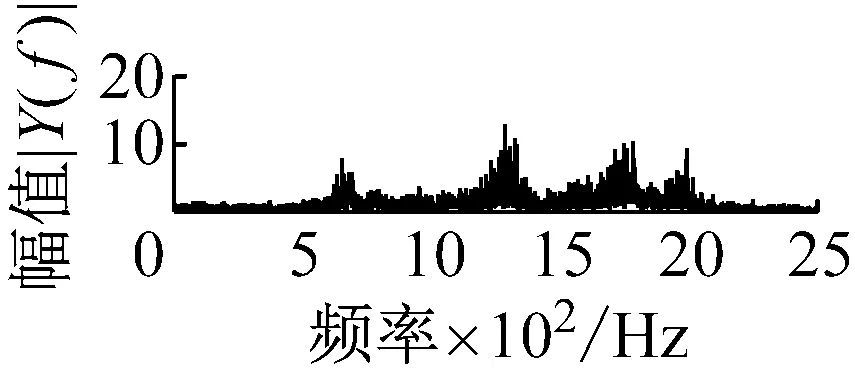
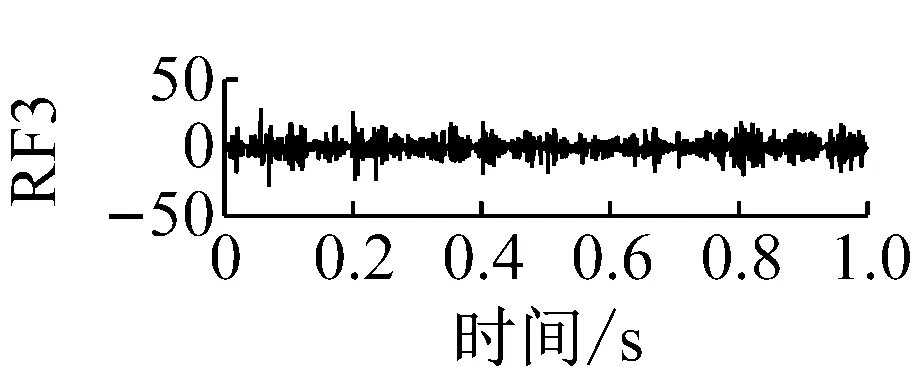
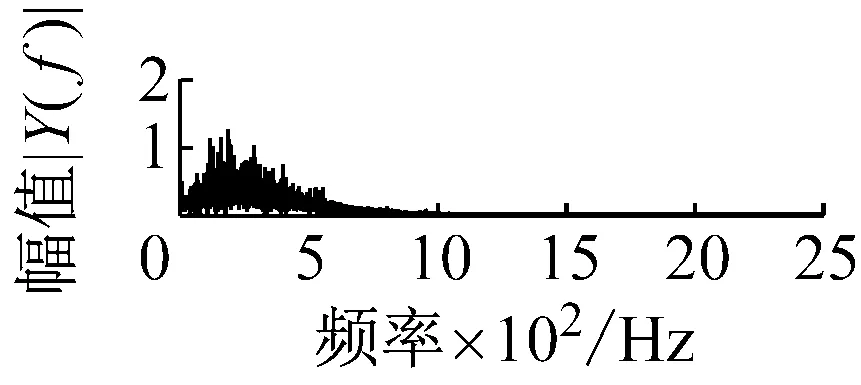
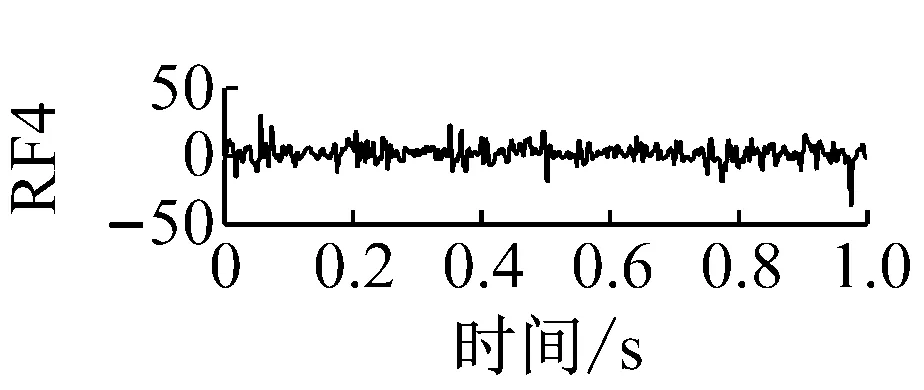
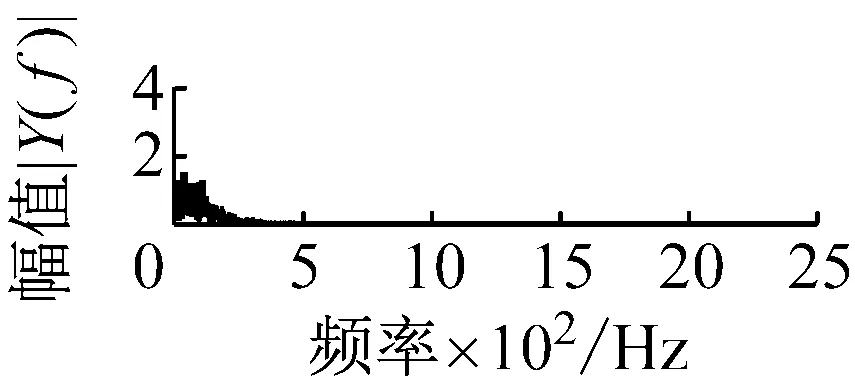
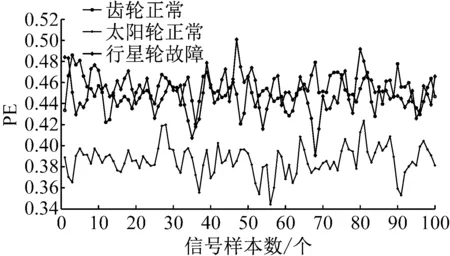
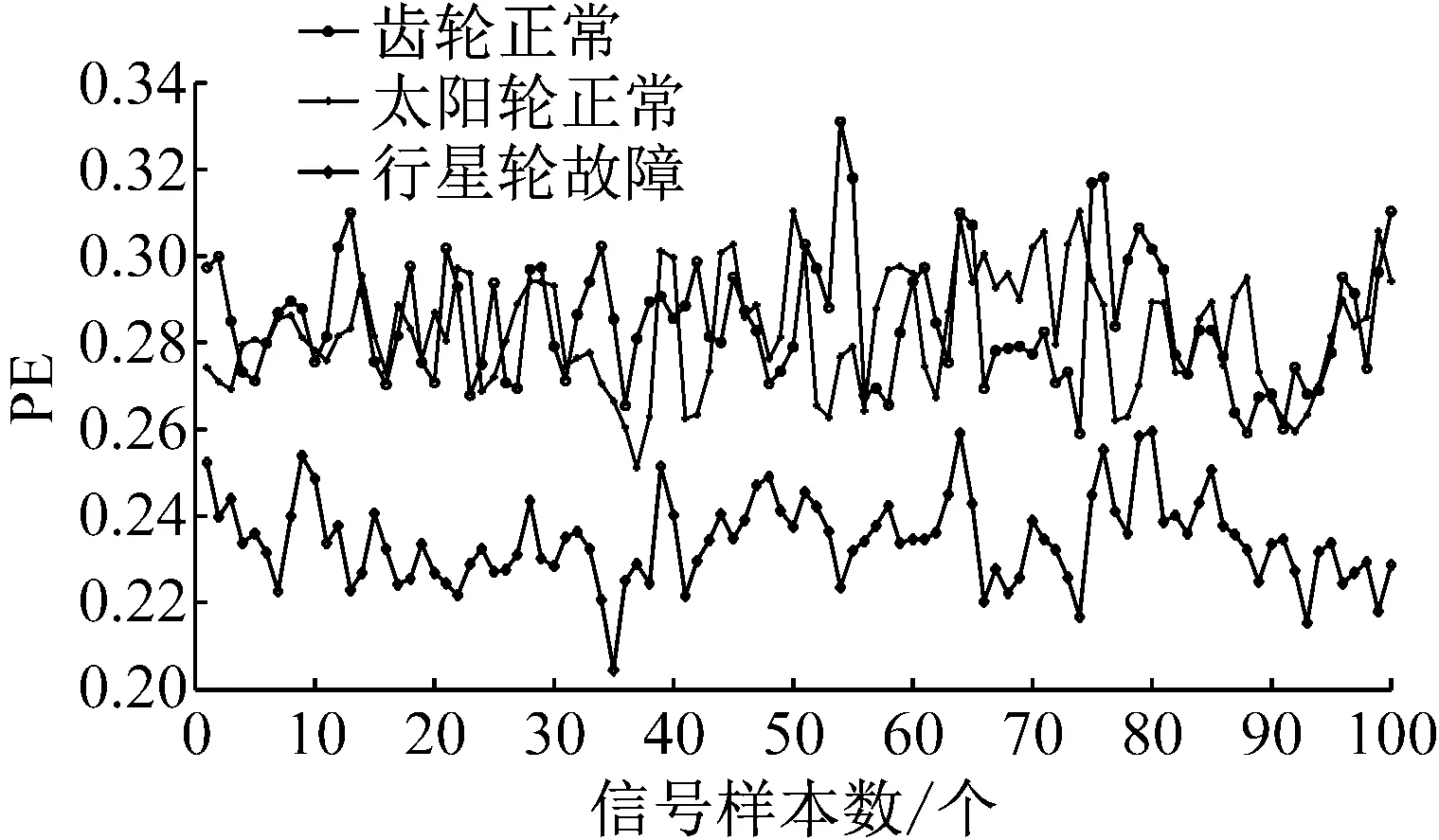
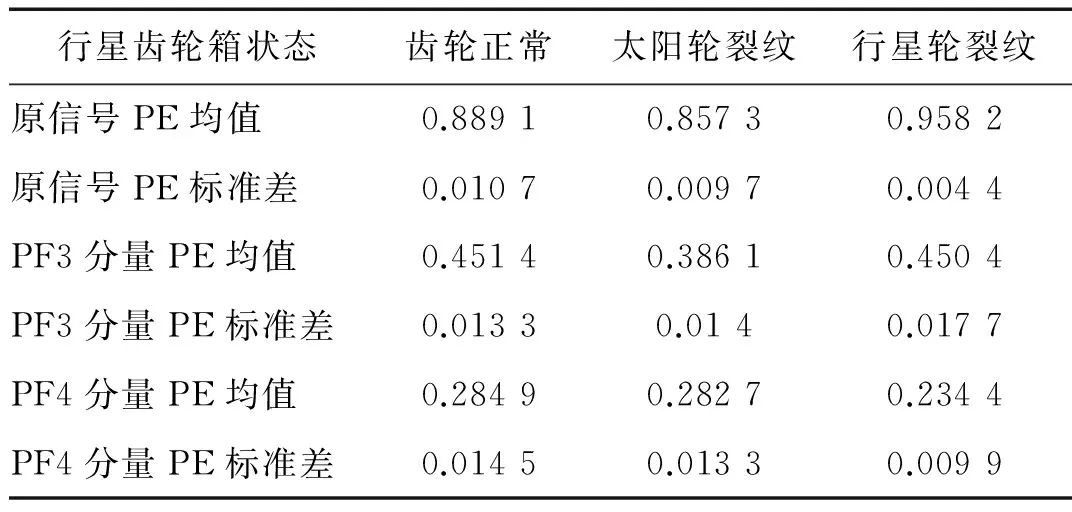
则根据ip和iq的大小排序，即当ip

x(j-(ip-1)τ)≤x(j-(iq-1)τ)

(5)

因此，对于重构矩阵Y的任一重构分量Y(j)都将得到一组位置索引序列

S(j)=(i1,i2,…,im)j=1,2,3,…,k

(6)

由于m维相空间映射不同的位置索引序列共有m!种，而各重构分量中升序排列序列可能存在相同，因此，k≤m!，其中S(j)为符号序列中的一种序列。

(3)计算熵值

计算每一种位置索引序列出现的概率p1,p2,…,pk，此时，时间序列X={x(i),i=1,2,3,…,n}的k种不同位置索引序列的排列熵(PE)可以根据信息熵的形式定义为

(7)

当pi=1/m!时，Hp(m)就达到最大值lnm!。

(4)归一化

为了方便各运行状态下的排列熵比较，通常用lnm!将Hp(m)进行归一化处理，即

Hp=Hp(m)/lnm!

(8)

式中，0≤Hp≤1。

Hp值的大小反映时间序列X的不确定程度:Hp的值越小，说明时间序列越确定，反之，则时间序列不确定性越大。Hp的变化反映了时间序列的微小细节变化。

在计算过程中，延迟时间τ和嵌入维度m的选取对于排列熵的计算结果将产生一定的影响，对于延迟时间τ和嵌入维度m的选取，装甲兵工程学院的冯辅周、司爱威和饶国强等人进行了深入的研究，使用以重构时间序列最佳相空间的方法确定模型参数，比较了不同确定方法对故障诊断结果的影响，最后得出参数模型独立确定方法优于联合确定方法，克服了排列熵参数人为主观或凭经验选择的不确定性[12]。

3 试验验证

为了检验上述基于LMD和排列熵算法在行星齿轮箱振动信号分析中的应用效果，使用试验验证其实用性。在行星齿轮箱故障诊断中，齿轮裂纹是一种常见的故障，若不及时发现将扩展成断齿，进而产生严重的后果，而齿轮裂纹故障信号微弱，对于齿轮裂纹的故障识别一直是一个难点，因此进行齿轮裂纹故障识别意义重大。本文分别对行星齿轮箱齿轮正常、太阳轮轮齿裂纹及行星轮轮齿裂纹三种状态进行故障模拟试验[13]，试验台示意图如图4所示，其中行星齿轮箱含有单一行星排，太阳轮为输入，行星架为输出。

图4 行星齿轮箱试验台

试验中，振动传感器粘贴在行星齿轮箱的箱体上，齿轮箱输入轴转速即太阳轮转速2 400 r/min，采集齿轮在正常、太阳轮裂纹及行星轮裂纹的行星齿轮箱振动信号数据，测试均在相同负载情况下完成，行星齿轮箱参数及各特征频率如表1所示，太阳轮啮合频率、太阳轮故障特征频率及行星轮故障频率的详细求解方法参照文献[14]，表1中的故障特征频率表示当太阳轮和行星轮出现裂纹故障时，实测信号在包含100 Hz和33.3 Hz的分量中存有故障信息。

采样频率设定为5 120 Hz，采样时间为1 s，齿轮正常、太阳轮裂纹及行星轮裂纹故障的时域和频域波形如图5所示。由此三种状态的频域波形可得，边频带集中在啮合频率和其倍频附近，故障信息并不明显，因此仅根据此时频域分析并不能判断行星齿轮箱是否存在故障。

表1 行星齿轮箱齿轮参数及频率

(a) 齿轮正常

(b) 太阳轮裂纹故障

(c) 行星轮裂纹故障

Fig.5 Time and frequency domain waveforms of normal and fault planetary gearboxes

文献[15]验证了基于EMD和排列熵在旋转机械中损伤检测具有较好的结果，图6为结合EMD和排列熵在行星齿轮箱振动分析中的检测结果，由图6可知，齿轮正常、太阳轮裂纹和行星轮裂纹排列熵值曲线出现多处交叉，均值无显著差异，因此无法判断各齿轮的故障情况，分析出现这一情况的原因可能是因为EMD对非线性非平稳信号适用性导致。

图6 三种状态下振动信号的EMD高频部分排列熵

Fig.6 PE of EMD high-frequency part of three conditions vibration signal

采用本文提出的方法，首先使用LMD方法对上述三种运行状态的振动信号进行分解，通过LMD分解可以将振动信号分解为包含不同频段的多个PF分量信号，而行星齿轮箱的故障信息有可能包含在某个PF分量中，然后通过排列熵算法对包含有故障信息的PF分量进行计算，从而检测出故障。为了确定包含故障信息的PF分量，对每个PF分量进行FFT变换，求其包含的频率成分。正常状态、太阳轮裂纹及行星轮裂纹的振动信号的分解结果及各个PF分量的频域波形分别如图7、图8和图9所示。

图7 齿轮正常状态下的LMD结果及频域波形

Fig.7 LMD result and frequency domain waveforms of vibration signal of normal gear

图8 太阳轮轮齿裂纹故障时的LMD结果及频域波形

Fig.8 LMD result and frequency domain waveforms of vibration signal of fault sun gear

由图7、图8和图9可知，包含行星齿轮箱啮合频率fm=667 Hz的高频振动信号及其倍频信号主要分布在PF1和PF2分量中，而包含频率100 Hz的振动信号主要分布在PF3分量中，包含频率33.3 Hz的低频振动信号主要分布在PF4分量中，当太阳轮或行星轮出现局部故障时，包含此两个频率点的主要分量中存在故障信息。因此，为了诊断太阳轮和行星轮是否发生局部故障，只需分别计算PF3和PF4分量的排列熵，根据排列熵的结果即可判断行星齿轮箱中太阳轮和行星轮的运行状态。

图9 行星轮轮齿裂纹故障时的LMD结果及频域波形

Fig.9 LMD result and frequency domain waveforms of vibration signal of fault planetary gear

在三种状态实测振动信号中，每种状态采集100个样本，选取每个样本的数据长度为L=1 024，使用LMD方法分别将此三种状态的100个样本自适应分解成多个PF分量，对各状态的PF3分量和PF4分量求取排列熵，根据参数模型独立确定方法确定嵌入维度m=5，延迟时间t=1，得出的排列熵值如图10和图11所示。

图10 三种状态下振动信号的PF3分量的排列熵

图11 三种状态下振动信号的PF4分量的排列熵

根据排列熵的概念，排列熵反映了一维时间序列的复杂度，此处反映齿轮振动信号的复杂度。在转速、负载相同的情况下，齿轮振动信号的排列熵越大，振动规律越随机；反之，排列熵越小，振动规律越确定。当齿轮出现故障时，信号将出现冲击，此时振动规律更确定，排列熵更小，因此如果某信号的排列熵小于正常信号的排列熵，则说明此信号为含有故障的信号。由图10可知，其中一种状态的PF3分量排列熵明显小于其他两种状态PF3分量的排列熵，说明了此PF3分量为含有故障的信号，而此分量的主要频率成分在100 Hz左右，由于太阳轮的故障特征频率为100 Hz，故判断此种状态太阳轮发生了故障，结果与实际吻合。由图11可知，其中一个状态的PF4分量排列熵明显小于其他两种状态PF4分量的排列熵，说明了此PF分量为含有故障的信号，而此分量的主要频率成分在33.3 Hz左右，由于行星轮的故障特征频率为33.3 Hz，故判断为行星轮出现了故障，结果与实际吻合。

为了更精准的比较这三种状态排列熵的差别，进一步证明结合LMD和排列熵方法的有效性，本文计算了未分解的原始信号、分解后的PF3分量和PF4分量的排列熵值均值以及其标准差值，计算结果，如表2所示。

表2 排列熵均值及标准差

由表2可知：

(1) 未经过LMD分解的原始信号的排列熵，行星齿轮裂纹故障的排列熵最大，太阳轮裂纹故障的排列熵最小，此结果并不能区分正常齿轮信号和故障齿轮信号，故不能作为判断行星齿轮箱的状态的依据。

(2) 在经过LMD分解后，PF3分量的排列熵中，太阳轮裂纹故障的排列熵明显小于齿轮正常和行星轮裂纹故障的振动信号排列熵，而在PF4分量中，行星轮裂纹故障的排列熵明显小于齿轮正常和太阳轮裂纹故障的排列熵，以此可作为判断行星齿轮箱运行状态的依据。

分析出现上述情况的原因可概括为，由于原始信号频率成分复杂，规律性较差，排列熵也没有规律，故而不能直接使用原始信号的排列熵作为判断行星齿轮箱的运行状态的依据。而在图10中，含有100 Hz的PF3分量中，齿轮正常和行星轮裂纹故障时，各齿轮啮合产生的冲击信号在PF3分量中没有明显的冲击，信号的差别是随机的，主要由齿面加工误差产生的表面不平度、波动度和齿形误差造成，故而能量分布的随机性强，不确定程度大，排列熵值高。而在太阳轮齿轮某个轮齿出现裂纹时，此轮齿刚度降低，齿轮在此轮齿啮合时将产生与其他轮齿啮合不同的冲击，且此啮合信号产生的冲击更具有确定性，冲击的频率为100 Hz，故在其含有此频率的PF3分量的排列熵更小，从而可判断太阳轮出现了故障。而在图11中，含有33.3 Hz的PF4分量中行星齿轮由于存在裂纹故障出现同样的状况，以此可诊断行星轮出现了故障，也进一步说明了基于LMD和排列熵的有效性。

4 结 论

本文提出一种行星齿轮箱故障诊断的新方法-基于LMD和排列熵的故障诊断方法，并运用这一算法对行星齿轮箱的振动信号数据进行处理，并得出以下结论：

(1)LMD作为一种近年来发展起来的自适应分解方法，能够有效的将非线性、非平稳信号自适应的分解为多个分频段的信号。排列熵作为一种新的数据处理方法，对于振动信号非常敏感，信号状态的微小变化都能够引起排列熵值的变化，且具有概念简单、计算简捷等特点。

(2)使用本文提出的基于LMD和排列熵的方法分解不同状态的振动信号，并对含有故障信息的PF分量求其排列熵可有效诊断行星齿轮箱的故障，判断其运行状态。

(3)由于基于LMD和排列熵的方法可将诊断结果定位到各频段，故而可用于行星齿轮箱的齿轮故障的诊断和识别，至于对除裂纹以外的其他故障的诊断，将做进一步的研究。

[1] 冯辅周，安钢，刘建敏．军用车辆故障诊断学[M]. 北京：国防工业出版社，2007：477-484．

[2] 雷亚国, 何正嘉, 林京, 等. 行星齿轮箱故障诊断技术的研究进展[J]. 机械工程学报, 2011, 47(19): 59-67.

LEI Yaguo, HE Zhengjia, LIN Jing, et al. Research advances of fault diagnosis technique for planetary gearboxes[J]. Journal of Mechanical Engineering, 2011, 47(19): 59-67.

[3] 孟宗, 李姗姗, 王亚超. 基于LMD和局域时频熵的旋转机械故障诊断方法[J]. 计量学报, 2015, 36(1):77-81.

MENG Zong, LI Shanshan, WANG Yachao. Method of rotating machinery fault diagnosis based on LMD and Local Time-frequency entropy[J]. Acta Metrological Sinica, 2015, 36(1):77-81.

[4] 于德介, 张嵬, 程军圣, 等. 基于EMD的时频熵在齿轮故障诊断中的应用[J]. 振动与冲击, 2015, 36(1):26-29.

YU Dejie, ZHANG Wei, CHENG Junsheng. Application of EMD and time-frequency entropy in gear fault diagnosis[J]. Journal of Vibration and Shock, 2015, 36(1):26-29.

[5] 杨斌, 程军圣. 基于LMD和主分量分析的齿轮损伤识别方法[J]. 振动、测试诊断, 2013, 33(5): 809-813.

YANG Bin, CHENG Junsheng. Method of gear damage identification based on LMD and principal component analysis[J]. Journal of Vibration, Measurement and Diagnosis, 2013, 33(5): 809-813.

[6] 程军圣, 杨宇, 于德介. 局部均值分解方法及其在齿轮故障诊断中的应用[J]. 振动工程学报, 2009, 22(1): 76-84.

CHENG Junsheng, YANG Yu, YU Dejie. LMD method and its application in gear fault diagnosis[J]. Journal of Vibration Engineering, 2009, 22(1): 76-84.

[7] BANDT C, POMPE B. Permutation entropy: A natural complexity measure for time series[J]. Phys. Rev. Lett., 2002, 88(174102): 1-4.

[8] CAO Y, TUNG W, GAO J B, et al. Detecting dynamical changes in time series using the permutation entropy[J]. Phys. Rev. E, 2004, 4(7): 1-7.

[9] 刘永斌,龙潜，冯志华，等.一种非平稳、非线性振动信号检测方法的研究[J].振动与冲击 2007，26(12)：131-134.

LIU Yongbin, LONG Qian, FENG Zhihua, et al. Detection method of nonlinear and non-stationary signals[J]. Journal of Vibration and Shock, 2007, 26(12): 131-134.

[10] 冯辅周,饶国强,司爱威,等. 排列熵算法研究及其在振动信号突变检测中的应用[J].振动工程学报.2012，25(2)：221-224.

FENG Fuzhou, RAO Guoqiang, SI Aiwei. Research and application of the arithmetic of PE in testing the sudden change of vibration signal[J]. Journal of Vibration Engineering, 2012，25(2)：221-224.

[11] 冯辅周，司爱威，饶国强，等．基于小波相关排列熵的轴承早期故障诊断技术[J] 机械工程学报，2012，29(3)：73-79．

FENG Fuzhou, SI Aiwei, RAO Guoqiang, et al. Early fault diagnosis technology for bearing based on wavelet correlation permutation entropy[J]. Journal of Mechanical Engineering, 2012，29(3)：73-79．

[12] 饶国强, 冯辅周, 司爱威, 等.排列熵算法参数的优化确定方法[J].振动与冲击，2014,33(1):188-193.

RAO Guoqiang, FENG Fuzhou, SI Aiwei, et al. Method for optimal determination of parameters in permutation entropy algorithm[J]. Journal of Vibration and Shock, 2014,33(1):188-193.

[13] LEI Yaguo, HAN Dong, LIN Jing, et al. Planetary gearboxes fault diagnosis using an adaptive stochastic resonance method[J].Mechanical Systems and Signal Processing, 2013, 38(1):113-124.

[14] 冯志鹏, 赵镭镭, 褚福磊. 行星齿轮箱齿轮局部故障振动频谱特征[J]. 中国电机工程学报, 2013, 33(5): 119-127.

FENG Zhipeng, ZHAO Leilei, CHU Fulei. Vibration spectral characteristics of localized gear fault of planetary gearboxes[J]. Proceedings of the CSEE, 2013, 33(5): 119-127.

[15] 冯辅周, 饶国强, 张丽霞, 等. 基于EMD和排列熵的轴承异常检测方法研究[J].轴承，2013(2):53-56.

FENG Fuzhou, RAO Guoqiang, ZHANG Lixia. Research on abnormality detection method for bearings based on EMD and permutation entropy[J]. Bearing, 2013(2):53-56.

Applicationoflocalmeandecompositionandpermutationentropyinfaultdiagnosisofplanetarygearboxes

DIND Chuang, ZHANG Bingzhi, FENG Fuzhou, JIANG Pengcheng

(Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

Nowadays planetary gearboxes are widely used in military and civilian equipment, so studying fault diagnosis of planetary gearboxes is very significant. Aiming at the nonlinearity and nonstationarity of planetary gearboxes’ vibrations, and the weakness of fault feature signals during their operation, a fault diagnosis method for planetary gearboxes was proposed based on the local mean decomposition (LMD) and the permutation entropy. The vibration signals under different conditions were adaptively decomposed into several product functions (PFs) with LMD. The corresponding permutation entropies of the PFs containing fault information were computed, they were used to identify fault types. Finally, three kinds of vibration signals for a planetary gearbox fault analog test platform were collected, they were the vibration signals in the gear normal state, those for the sun gear with a cracked tooth and those for the planet gear with a cracked tooth. These vibration signals were decomposed with LMD and the corresponding permutation entropies were computed, the effectiveness of the proposed method was verified.

planetary gearbox; local mean decomposition (LMD); permutation entropy; fault diagnosis

国家自然科学基金(51205407)

2016-04-01 修改稿收到日期：2016-06-26

丁闯 男，博士生，1989年5月生

冯辅周 男，博士，教授，1971年3月生

TH212；TH213

： A

10.13465/j.cnki.jvs.2017.17.009