内共振作用下轴向运动黏弹性梁横向受迫振动
2017-09-25黄玲璐毛晓晔陈立群
黄玲璐, 毛晓晔, 丁 虎, 陈立群,2
(1.上海大学 上海市应用数学和力学研究所, 上海 200072; 2.上海大学 力学系,上海 200444)
内共振作用下轴向运动黏弹性梁横向受迫振动
黄玲璐1, 毛晓晔1, 丁 虎1, 陈立群1,2
(1.上海大学 上海市应用数学和力学研究所, 上海 200072; 2.上海大学 力学系,上海 200444)
研究内共振与外部激励共同作用下,轴向运动黏弹性梁横向非线性振动的稳态响应。在运动梁动力学建模中采用Kelvin本构关系,并取物质时间导数。首次将直接多尺度法应用到轴向运动连续体的内共振研究。通过直接对连续体的偏微分-积分控制方程运用多尺度法,建立内共振条件下的横向非线性受迫共振的可解性条件。并通过稳定性分析,得到稳态响应解的稳定边界。另外还考察了参数对响应的影响。运用数值仿真验证了近似解析方法的正确性及有效性。
轴向运动梁;内共振;受迫振动;直接多尺度法
在工业生产和工程实际中,存在许多轴向运动的工程系统,例如动力传送带、带锯、高楼升降机缆绳、空中缆车索道、发动机中的张紧皮带等。通常这些系统都可以建模为沿着轴向运动的梁或者弦线,当系统的抗弯刚度不可忽略时,这些工程系统元件均可以模型化为轴向运动梁。因此,对于轴向运动梁的研究具有广泛应用前景。国内外学者也对此进行了很多有意义的研究[1-4]。
Ding等[5]研究了亚临界状态下轴向运动梁非线性振动的固有频率,比较了两组横向模型与平面耦合模型。吕海炜等[6]研究了轴向运动软夹层梁的横向振动特性。随着研究的深入,学者们开始聚焦于内共振对轴向运动体非线性动力学的影响。冯志华等[7]对满足3∶1内共振条件的轴向运动梁的参激振动平凡解稳定性进行了分析。陈树辉等[8]研究得到了轴向运动梁内共振复杂的频率-振幅响应曲线。Ghayesh等[9-15]对轴向运动Euler梁的内共振下的受迫振动稳态响应进行了研究。需要说明的是,以后的研究大都是将运动体横向振动的非线性控制方程进行Galerkin截断,再对截断后的多自由度非线性常微分方程组进行进一步的分析。直接对非线性偏微分(-积分)方程进行分析,以研究内共振条件下轴向运动梁受迫振动的相关研究还很罕见。
本文运用直接多尺度法研究3∶1内共振条件下的轴向运动黏弹性梁横向非线性受迫振动的稳态响应,并运用数值方法对近似解析解进行了验证。
1 控制方程
考虑如图1所示的两端简支的轴向运动梁,其截面积为A,长度为L,密度为ρ,初始张力为P,并以一致的恒定速度Γ沿轴向移动,考虑外部存在简谐激励F=Bsin(Ωt),其中B和Ω分别为激励的幅值和频率。当满足I/(AL2)<0.001时,用Euler-Bernoulli梁模型来描述梁的动力学特性已经足够精确。

图1 轴向运动梁物理模型
根据广义的哈密顿原理建立轴向运动梁横向振动控制方程:
ρA(V,TT+2V,TXΓ+Γ2V,XX)+M,XX-PV,XX-
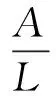
(1)
式中:V(X,T)为梁的横向位移;σ(X,T)和M(X,T)分别为梁沿轴向分布的附加应力和弯矩。黏弹性本构关系为Kelvin模型并取物质时间导数,该轴向运动黏弹性梁的应力和应变的关系为
(2)
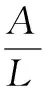
(3)
简支边界条件为
V(0,T)=V(L,T)=0,V,XX(0,T)=V,XX(L,T)=0
(4)
为将式(3)无量纲化,引入空间和时间的坐标变换及新的参数:
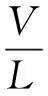
(5)
(6)
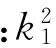
利用式(5)和式(6),对式(3)进行无量纲化,得到:
γv,xxxxx)=bsin(ωt)+
(7)
相应的边界条件变为
(8)
1.1固有频率及内共振条件
忽略方程(7)中的非线性部分,得到运动方程的派生系统:
(9)
方程(9)的四自由度解写为
(10)
cc表示等号右端前四项的共轭复数,其中模态函数为
(11)
将四自由度解以及模态函数代入派生系统方程中,依次乘以sin(mπx),并对x从0到1积分,按照exp(Iωnt)归纳整理可到一下四个方程:
(12)
(13)
(14)
(15)
式中:
(16)
为满足式(12)~(15),exp(Iωnt)的系数必须为零,由此可以得到16个方程构成的方程组。而cn,m不可能全部为0,由线性代数知识可知其Jacobi矩阵行列式值必然为0
(17)
由此系统固有频率以及3∶1内共振条件可以解出。
选取常用V带作为具体研究对象,其物理参数GB/T 1171—1996,如表1所示。

表1 V带的物理参数
V带的横截面如图2所示。
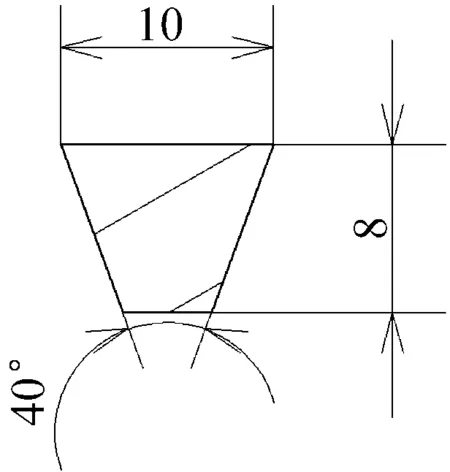
图2 V带的横截面
根据表1的物理参数求得3∶1内共振条件以及前四阶固有频率,如表2所示。

表2 派生系统的前四阶固有频率
2 主共振响应
对式(7)应用直接多尺度法,先对方程引入重刻度,使得非线性恢复力、阻尼力以及外激励出现在同一个方程中:
b=ε3b,α=ε2α,v(x,t)=εv(x,t)
(18)
由于控制方程中只有立方非线性,可以设控制方程的解为
v(x,T0,T2)=v0(x,T0,T2)+ε2v2(x,T0,T2)
(19)
式中:T0=t表示对应于无黏弹性阻尼的和外激励的线性系统以固有频率ωn运动时的快时间尺度,T2=ε2t表示更慢的时间尺度;这是因为阻尼和外激励而引发的振幅及相位慢变。将式(19)及关于t的导数
(20)
代入式(7),并提取ε0和ε2项系数,令它们的系数为零得到:
(21)
2γv0,T2x+2v0,T0T2+v2,T0T0+2γv2,T0x-
(22)
式(21)为齐次线性偏微分方程,其解可以写成:
v0(x,T0,T2)=A1(T2)Θ1(x)eIω1T0+
A2(T2)Θ2(x)eIω2T0+cc
(23)
式中:cc表示等号右端前两项的共轭复数;ω1、ω2为固有频率;An(T2)为待定函数;Θ1、Θ2为模态函数,其表达式为
Θn(x)=pn,1sin(πx)+pn,2sin(2πx)+
pn,3sin(3πx)+pn,4sin(4πx),

(24)
将式(23)和式(24)代入方程(21),用待定系数法求出模态函数中系数pn,m,以及pn,m的共轭复数。
为表示第二阶固有频率离开ω2的程度以及扰动频率ω离开ω1的程度,引入调谐参数σ1、σ2,
ω2=3ω1+ε2σ1,ω=ω1+ε2σ2
(25)
将式(21)的解v0代入方程(22)中,寻求陀螺系统的可解性条件,由于只需去除方程中的长期项,因此仅需考虑方程的齐次解,可将式(22)的解写成:
v2(x,T0,T2)=Q1(x,T2)eIω1T0+Q2(x,T2)eIω2T0
(26)
(27)
将式(23)和式(26)代入方程(22),利用(25)的关系,内积后分别提取等号两边exp(iω1T0)以及exp(iω2T0)系数,可以得到:
(28)
式中:Hn,m是指数项系数中不含qn,m的部分,将列向量替换qn,m系数矩阵中任意列,即可得到可解条件。
引入待定函数A1,A2的极坐标表达式
(29)
式中:an表示响应幅值;θn表征响应的相角。将皮带数值代入,可以得到无量纲刚度kf=0.2,无量纲非线性系数k1=23.8,无量纲阻尼系数α=0.001,无量纲激励幅值b=0.01,梁的无量纲速度取γ=0.511 26,求得可解性条件如下:

7.287 587 915×106a1σ2-6.869 475 935×108Iαa1-
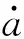
(30)

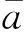
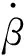

1.521 519 152×1010Iαa2=0
(31)
分离方程(30)的实部虚部得到:-6.869 475 935×108αa1-1.309 834 7×106bcos(β2)+
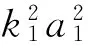
(32)
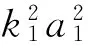
7.287 587 915×106a1σ2-1.945 387 102×
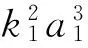
(33)
分离方程的实部虚部得到:
1.521 519 152×1010αa2=0
(34)
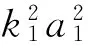
4.780 311 616×107a2σ2+1.593 437 205×107a2σ1-
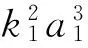
(35)
从式(32),(33),(34),(35)中消去相角,得到幅频响应方程并用数值仿真结果验证。
3 数值验证
上节用直接多尺度方法得到了稳态周期解的幅频响应方程,本节采用龙格-库塔法,对四阶截断方程进行仿真,以验证解析方法的有效性以及正确性。
选取与解析过程中相同的黏弹性梁参数,将仿真结果与解析解画在同一副图中,如图3所示。图3中虚线是稳定边界,采用劳斯-霍尔威兹判据,由式(32)和式(33)计算得到。在该边界内的区域响应不稳定,而区域外响应稳定。扫频仿真中,上一步的稳态作为下一步计算的初始值,以考察初始值对非线性跳跃区域的影响。观察图3可以发现在不稳定的区域内,幅频响应会出现跳跃现象,且系统的非线性呈硬特性。此外,从图中可以看出,近似解析分析和数值仿真吻合得较好,由此验证了近似解析分析结果的有效性及正确性。
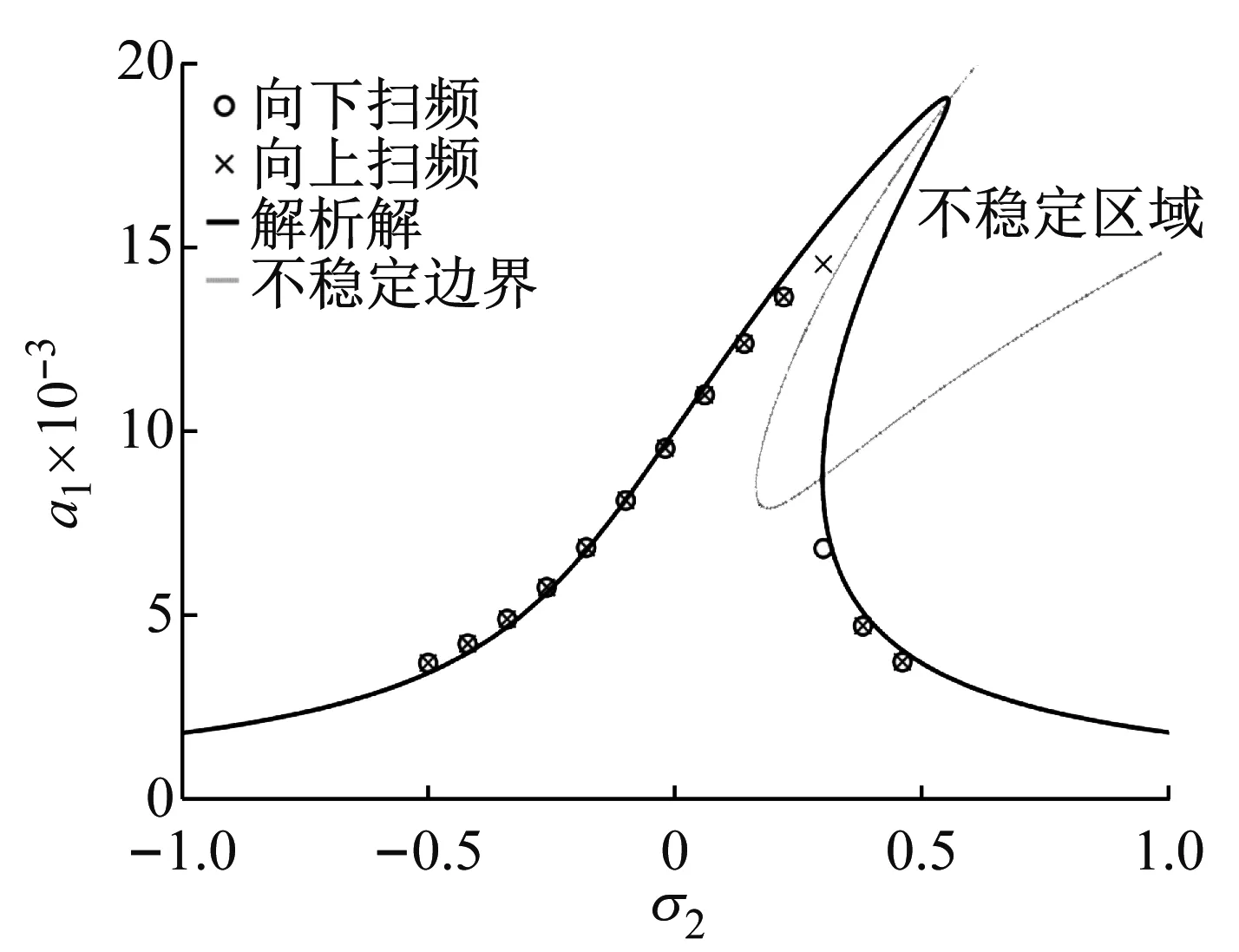
图3 一阶主共振时幅频响应曲线
利用解析方法,不仅可以得到稳态响应幅频曲线,在主共振附近任意频率上都可以解出响应的响应幅值及相角,进而可以得到此时的时域响应曲线。同样,解析结果的正确性用仿真结果验证,如图4所示。
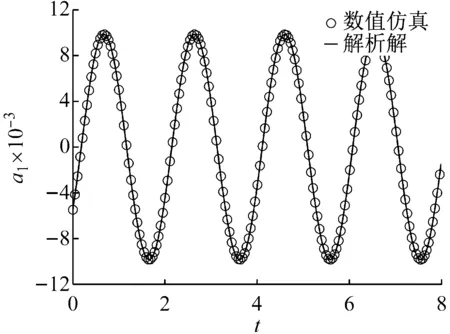
图4 一阶主共振时时域响应曲线
图4中,实线代表解析解,圆圈代表仿真得到的时域响应曲线,可以发现解析与仿真结果吻合非常好,又一次验证了解析方法的有效性及正确性。
4 非线性参数影响及滞后现象
与线性系统不同,非线性系统的共振峰会产生弯曲,非线性越强,弯曲幅度越大。通过更改幅频响应方程中的非线性系数,得到三组非线性参数下的幅频响应曲线,以考察非线性系数对系统响应的影响。从图5所示的幅频响应曲线中,可以观察发现当非线性系数超过一定范围时,幅频响应曲线存在多值区域,也就是跳跃现象。从图5中还可以发现,虽然非线性系数呈等差关系,但是,随着非线性系数的增加,共振峰的弯曲幅度呈非线性增长。因此,非线性系数对轴向运动梁的动力学特性影响非常显著。

图5 非线性参数对幅频响应的影响
为了考察外激励幅值的影响,图6给出了是一阶主共振时第一阶模态响应幅值在不同激励频率下随外激励幅值的连续变化曲线。观察发现,当解谐参数大于某一个临界值时,幅值曲线才会出现多值现象,这也称之为滞后现象。一般来说,滞后现象发生的条件与系统非线性特性是密切相关的。本文研究的非线性特性表现为硬特性,即稳态幅频响应曲线向右弯曲。因此,也只有外部激励的频率在大于固有频率时才会发生滞后现象。

图6 一阶主共振第一阶模态滞后曲线
图7是一阶主共振时第二阶模态的滞后曲线。图8是对图7的局部的放大。观察图7可以发现,同样只有在激励频率大于固有频率时才会出现滞后现象。这是由系统前两阶模态满足3∶1内共振的耦合作用引起并决定的。实际上,第一阶模态多值区间与第二阶模态的多值区间有共性。但是,对比发现,与第一阶模态不同的是,当外部激励的幅值超过一个临界值后,第二阶模态上的响应将不再变化,这称之为饱和现象。这种能量在不同模态间的转移是内共振所特有的。
5 结 论
本文运用直接多尺度方法研究了轴向运动黏弹性梁横向非线性受迫振动,主要考察了内共振对系统稳态响应的影响,特别是能量在不同模态间的转移。在直接多尺度的应用过程中,考虑了陀螺系统的特点,计入了轴向运动梁前四阶的模态,而非传统做法中的两阶模态。解析方法的有效性及正确性得到了仿真结果的验证。研究结果表明,非线性参数对幅频响应的影响非常大,跳跃现象以及滞后现象只发生在外激励频率大于固有频率的条件下,同时,还发现了二阶模态响应中内共振特有的饱和现象。

图7 一阶主共振第二阶模态滞后曲线
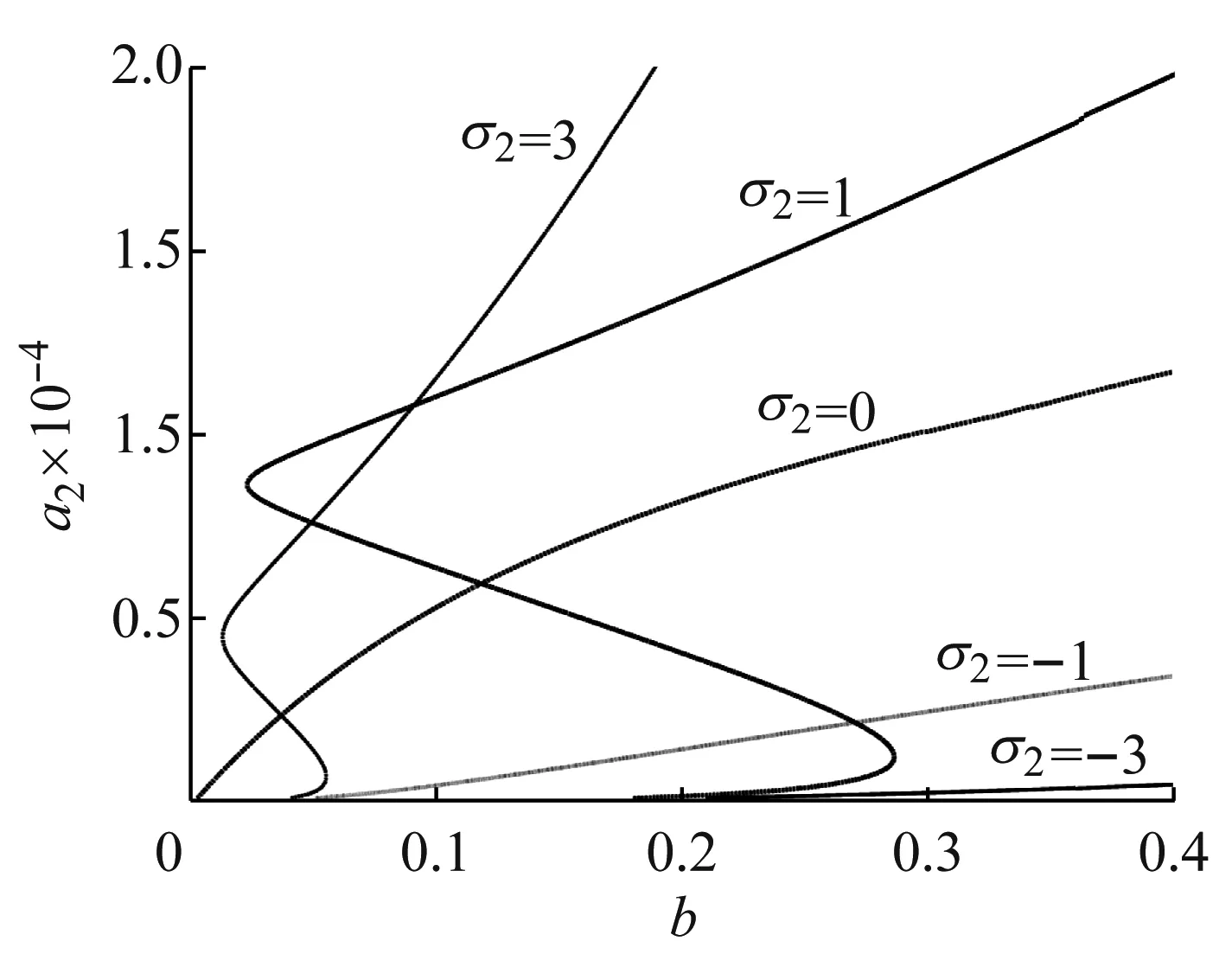
图8 一阶主共振第二阶模态滞后曲线局部放大
[1] MOTE JR C D. Dynamic stability of axially moving materials[J]. Shock and Vibration Digest, 1972, 4(4): 2-11.
[2] WICKERT J A. Non-linear vibration of a traveling tensioned beam[J]. International Journal of Non-Linear Mechanics, 1992, 27(3): 503-517.
[3] 丁虎, 陈立群. 轴向运动黏弹性梁横向非线性受迫振动[J]. 振动与冲击, 2009, 28(12): 128-131.
DING Hu, CHEN Liqun. Transverse non-linear forced vibration of axially moving viscoelastic beam[J]. Journal of Vibration and Shock, 2009, 28(12): 128-131.
[4] 宫苏梅, 张伟. 平带系统非线性振动实验研究[J]. 动力学与控制学报, 2014, 12(4): 368-372.
GONG Sumei, ZHANG Wei. Experimental study on nonlinear vibration of flat-belt system[J]. Journal of dynamics and Control, 2014, 12(4): 368-372.
[5] DING H, CHEN L Q. Natural frequencies of nonlinear vibration of axially moving beams[J]. Nonlinear Dynamics, 2011, 63(1/2): 125-134.
[6] 吕海炜, 李映辉, 李亮, 等. 轴向运动软夹层梁横向振动分析[J]. 振动与冲击, 2014, 33(2): 41-51.
LÜ Haiwei, LI Yinghui, LI Liang, et al. Analysis of transverse vibration of axially moving soft sandwich beam[J]. Journal of Vibration and Shock, 2014, 33(2):41-51.
[7] 冯志华, 胡海岩.内共振条件下直线运动梁的稳定性[J]. 力学学报, 2002, 34(3):389-400.
FENG Zhihua, HU Haiyan. Dynamics stability of a slender beam with internal resonance under a large linear motion[J]. Acta Mechanica Sinica, 2002, 34(3): 389-400.
[8] 陈树辉, 黄建亮. 轴向运动梁非线性振动内共振研究[J].力学学报, 2005, 37(1): 57-63.
CHEN Shuhui, HUANG Jianliang. On internal resonance of nonlinear vibration of axially moving beams[J]. Acta Mechanica Sinica, 2005, 37(1): 57-63.
[9] GHAYESH M H, KAZEMIRAD S, AMABILI M. Coupled longitudinal-transverse dynamics of an axially moving beam with an internal resonance[J]. Mechanism and Machine Theory, 2012, 52: 18-34.
[10] GHAYESH M H. Nonlinear forced dynamics of an axially moving viscoelastic beam with an internal resonance[J]. International Journal of Non-Linear Mechanics, 2011, 53: 1022-1037.
[11] GHAYESH M H, KAFIABAD HA, REID T. Sub-and super-critical nonlinear dynamics of a harmonically excited axially moving beam[J]. International Journal of Solids and Structures, 2012, 49: 227-243.
[12] RIEDEL C H, TAN C A. Coupled, forced response of an axially moving strip with internal resonance[J]. International Journal of Non-Linear Mechanics, 2002, 37: 101-116.
[13] CHEN S H, HUANG J L, SZE K Y. Multidimensional Lindstedt-Poincaré method for nonlinear vibration of axially moving beams[J]. Journal of Sound and Vibration, 2007, 306: 1-11.
[14] HUANG J L, SU R K L, LI W H, et al. Stability and bifurcation of an axially moving beam tuned to three-to-one internal resonances[J]. Journal of Sound and Vibration, 2011, 330: 471-485.
[15] SZE K Y, CHEN S H, HUANG J L. The incremental harmonic balance method for nonlinear vibration of axially moving beams[J]. Journal of sound and Vibration, 2005, 281: 611-626.
Transversenon-linearforcedvibrationofanaxiallymovingviscoelasticbeamwithaninternalresonance
HUANG Linglu1, MAO Xiaoye1, DING Hu1, CHEN Liqun1,2
(1.Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China;2.Department of Mechanics, Shanghai University, Shanghai 200444, China)
The transverse nonlinear forced vibration of an axially moving viscoelastic beam with a three-to-one internal resonance was analytically and numerically studied here. The beam material obeys Kelvin constitution relation model with material time derivatives adopted. For the first time, the multi-scale method was used to study the internal resonance of the axially moving continuous beam. The solvability condition for the transverse nonlinear forced vibration of the beam was derived under the internal resonance condition. The stable boundary for the beam’s steady-state response solution was obtained with the stability analysis. The effects of the system parameters on the beam’s steady-state response were examined. Finally, the correctness and effectiveness of the proposed approximate analytical method were verified with numerical simulations.
axially moving beam; internal resonance; forced vibration; multi-scale method
国家自然科学基金重点项目(11232009);国家自然科学基金(11372171;11422214)
2016-01-13 修改稿收到日期:2016-06-24
丁虎 男,博士,教授,博士生导师,1978年3月生 E-mail:dinghu3@shu.edu.cn
O322
: A
10.13465/j.cnki.jvs.2017.17.011
