基于时频脊线旋转匹配的多普勒矫正方法研究

刘星辰， 胡智勇， 何清波， 朱 军

(中国科学技术大学 精密机械与精密仪器系，合肥 230027)

基于时频脊线旋转匹配的多普勒矫正方法研究

刘星辰， 胡智勇， 何清波， 朱 军

(中国科学技术大学 精密机械与精密仪器系，合肥 230027)

多普勒效应使信号产生畸变，增加了道旁高速列车声学故障诊断的难度。时域重采样是一种有效的多普勒畸变矫正方法，该方法需要对时间中心有一个准确估计。在深入分析多普勒畸变信号瞬时频率变化特征的基础上，提出一种新的多普勒畸变校正方法。用时频融合技术提高时频图的分辨率，对时频脊线旋转匹配以获得时间中心，从而求得重采样序列用以校正多普勒畸变。仿真信号和实验信号分析结果表明，该方法能有效实现多普勒矫正，在道旁声学故障诊断中有一定的可行性。

故障诊断；多普勒畸变；声学信号；时频图旋转匹配

轴承故障在传统机械设备故障类型中占据着很大的比重[1-4]。随着铁路运输业的快速发展，列车的安全性问题日益严峻。根据美国的一项统计，作为列车故障的主要类型，列车轴承故障每年引发大约50起出轨事故[5]。所以，实现对列车轴承的准确诊断，对于减少事故的发生与保障列车的安全运行具有深远意义。

列车道旁声学诊断系统发展于20世纪80年代[6]，具有低成本以及能检测早期故障等优点，然而也存在故障误判、漏判以及难以定位故障等缺点[7]，从而导致一些灾难性的后果。在这个系统中，由于麦克风所在的位置与铁轨之间的位置不可忽略，另外在列车高速行驶时轴承与麦克风之间存在横向相对速度，从而使测量信号产生多普勒畸变，造成被测信号的频移、幅值调制以及频带展宽等问题[8]，这为基于频率分析的故障诊断带来了难度，需要对其进行校正[9-10]。

多普勒效应广泛存在于需要处理运动声源所产生声学信号的领域，国内外的研究人员提出了一系列解决方法。Dybala提出一种动态信号重采样方法，该方法基于希尔伯特变换，能消除道旁故障诊断系统所受多普勒效应的影响，但该方法在频域处理时只能处理单一的频率成分，对于密集频率成分难以处理；刘方等[11]结合了时域重采样的多普勒校正方法和整体平均经验模态分解技术，但是与时域重采样有关的参数需要提前获得，这就限制了该方法的实际应用；张翱等[12]提出了一种能量重心法来对瞬时频率进行估计，进而实现多普勒畸变信号的校正，然而这种方法受噪声的影响较大，噪声大时瞬时频率的提取会非常困难，参数估计也会产生较大偏差；张海滨等[13-14]提出一种基于伪时频分布的方法对中心频率和时间中心进行了估计，然后进行多普勒校正，然而这种方法运算量较大。

为了增强获取多普勒声学畸变信号的参数过程中对噪声的鲁棒性，同时从实际应用过程中减少参数测量的角度考虑，本文提出了一种基于时频脊线旋转匹配的方法，该方法首先对不同分辨率的时频图进行融合，使得随机噪声得到了很好地抑制，另外同时提高了时间和频率两个方面的分辨率[15]；通过对时频脊线进行旋转，将旋转后的时频脊线与原时频脊线进行匹配，进而获得时间中心；随后利用获得的这一参数通过时域重采样技术对信号的多普勒畸变进行校正并进行后续的诊断分析。最后本文构造了仿真信号对该方法进行验证，并将其应用于实际的列车轴承故障信号分析，仿真及实验结果都证明了该方法的有效性。

1 相关理论模型与原理分析

1.1道旁声学诊断模型

列车的道旁声学故障诊断模型如图1所示，被测声源在t=0时刻从相对于麦克风水平距离S处出发，以相对于空气介质为v的速度沿着图示方向运动。R(t)表示t时刻麦克风到声源的距离，θ(t)表示列车前进方向与声源连线间的夹角，r为麦克风与声源前进方向的垂直距离。

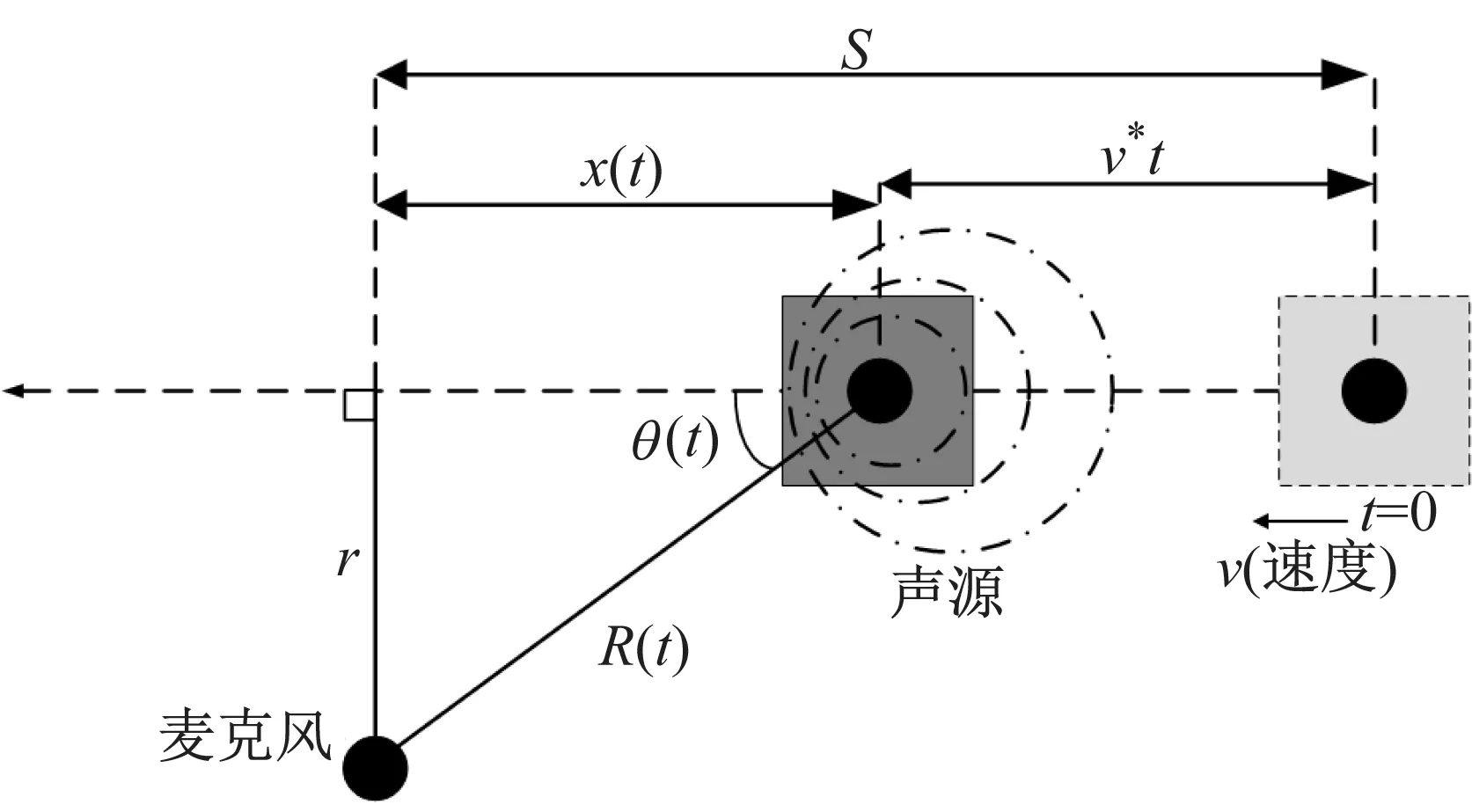
图1 道旁声学诊断模型

在理想情况下，不考虑空气的黏滞阻力，无能量损耗，另外列车速度不高于声速，声源波动方程以简谐波q(t)=q0sinω0t给出，根据莫尔斯声学理论[16]，t时刻麦克风所采集到的声压方程P(t)可由式(1)表示如下：

(1)

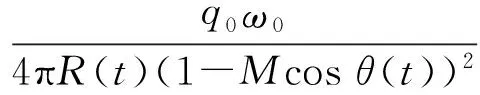
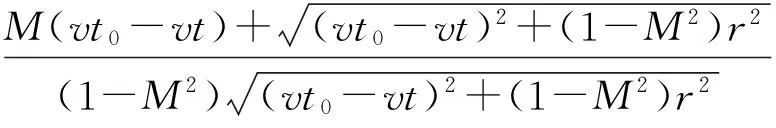
(2)

式中，t0表示多普勒信号的时间中心，且满足S=vt0。从式中可知麦克风所接收到的信号与原信号相比出现非线性畸变，我们所提出的方法就是针对这种畸变进行校正。

1.2时域重采样校正多普勒畸变

时域重采样是一种常用的校正多普勒畸变的方法，该方法关键在于建立重采样时间序列。假设声源在t时刻到麦克风的距离为R，则麦克风经过时间R/c后才能接收到该时刻声源发出的声音，即：

tr=t+R/c

(3)

将R表达式代入，有：

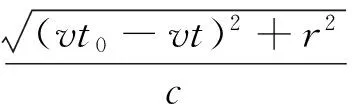
(4)

利用式(4)即可计算麦克风接收时间序列并作为插值时间序列来对采集到的多普勒畸变信号进行插值重采样。同时可以看出，重采样时间序列的构建完全由时间中心t0、声源速度v和麦克风到声源运动的垂直距离r决定，而v和r较为容易获得，所以本文把工作重点放在获取时间中心t0上。

1.3时频数据融合

这项技术首先由Peng提出用来克服传统时频分析方法的固有缺陷。根据海森堡不确定性准则，当时频图的频率分辨率提高时，时间分辨率就会降低；反之，时间分辨率的提高也会导致频率分辨率的降低。而时频数据融合技术能很好地解决这个问题，既能提高在频率轴方向上的分辨率，又不会以降低时间轴方向上的分辨率为代价。

时频数据融合步骤如图5中第一步所示。首先使用不同窗宽对信号进行短时傅里叶变换(Short Time Fourier Transform)获得两组时频分布如图2所示：图2(a)的窗宽为127，具有较高的时间分辨率以及较低的频率分辨率；图2(b)的窗宽为511，具有较低的时间分辨率以及较高的频率分辨率，输入时频数据融合引擎，其融合规则如式(5)所示，最终得到的时频分布如图7其时间、频率准确性均高于原始分布。

|TFDori(t,f)|=

(5)

式中：a=|TFD1(t,f)|×|TFD2(t,f)|，Th(f)作为阈值可以起到消除输入信号背景噪声的作用，其值的选取取决于噪声的大小。

2 多普勒信号的时频脊线旋转匹配

根据莫尔斯声学理论[16]，声源在接近和远离麦克风过程中，麦克风所接收到的信号频率畸变具有相反的变化规律，在时频图上就表现为时频脊线关于时间中心t0对称。如图3所示。当时间中心t0位于时频图中时域中点时，时频脊线是完全中心对称的；当时间中心t0在时频图上偏左或偏右时，时频脊线右边或左边(以时间中心t0为界)会长于另外一边，忽略过长的那一段仍然表现出关于时间中心t0的对称性。

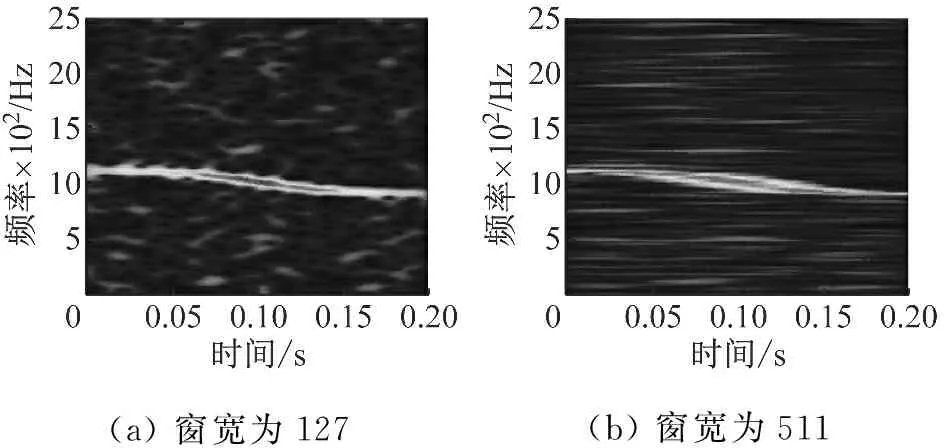
(a)窗宽为127(b)窗宽为511

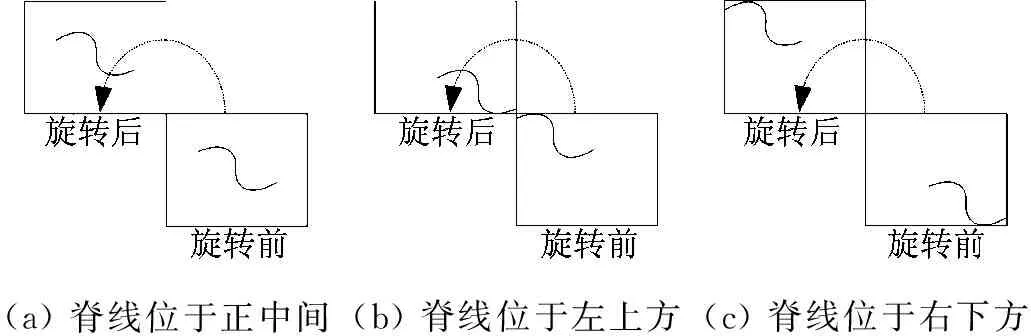
图2 使用不同窗宽所做STFT获得的时频表示

图3 三种不同情况下时频图旋转后与旋转前的结果

Fig.3 Comparison of TFR before and after rotation under 3 kinds of different circumstances

根据这一特性，我们提出一种全新的搜索时间中心的方法：首先将时频图旋转180°，然后将旋转后的时频图逐点移动后与原时频图进行匹配。理论上当二者的时间中心重合时，具有最佳的匹配度，反之根据出现最佳匹配度时时频图所移动的距离col，就可以推算出时间中心t0所在的位置。如图4所示，存在关系式2t0=col/fs，即

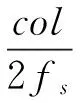
(6)

式中，fs表示采样频率。

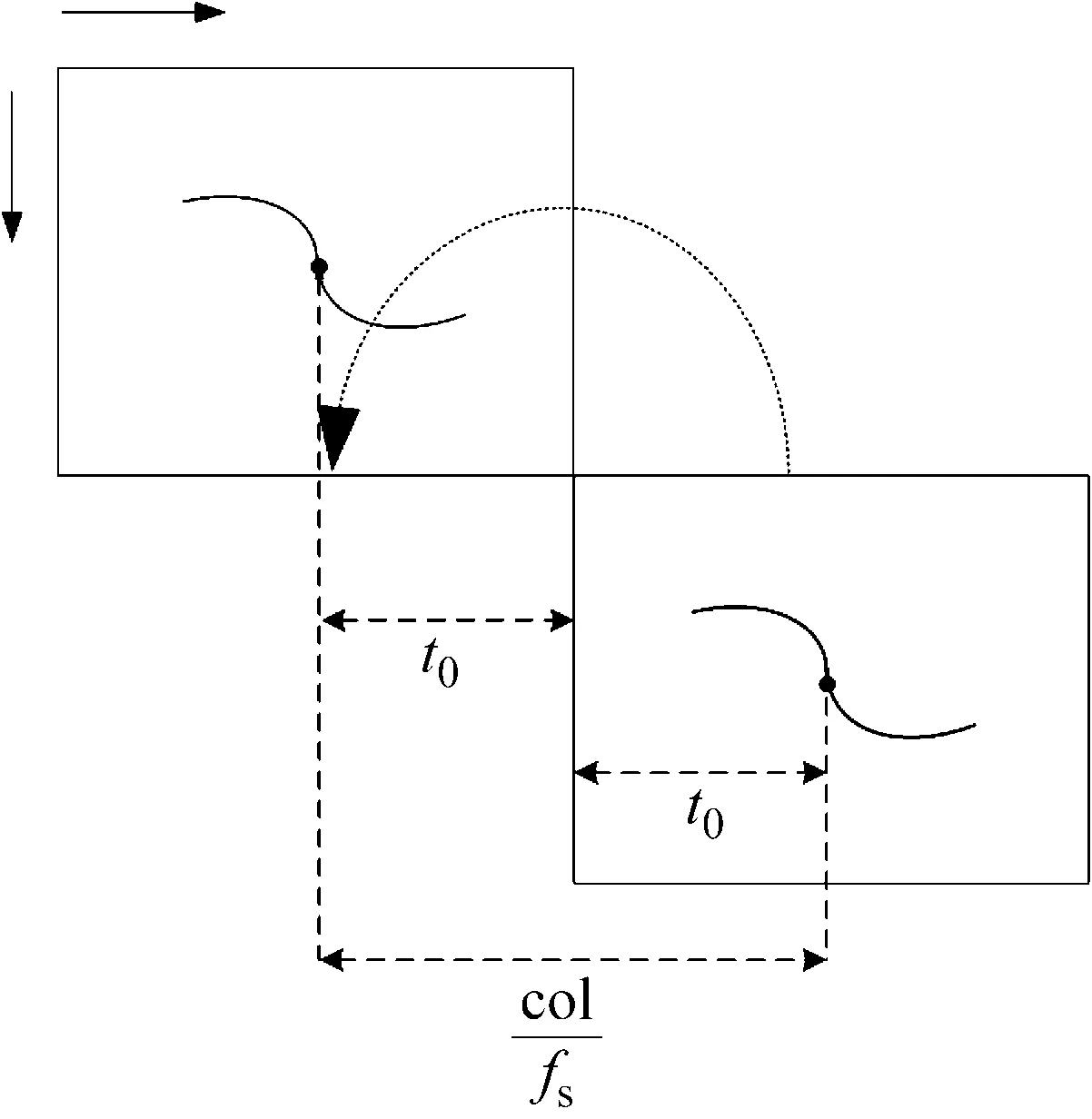
图4 时频脊线旋转匹配搜索时间中心的原理示意

Fig.4 Schematic of time center searching based on rotation matching of time-frequency ridge

3 基于时频脊线旋转匹配的畸变矫正和仿真信号分析

3.1多普勒畸变信号校正流程

根据前文的分析结果，总结出对存在多普勒畸变的信号进行校正的步骤如下：

(1) 获取存在多普勒畸变的原始信号和相关系统参数的测量值；

(2) 用不同的窗宽对信号做STFT获得两组不同时间和频率分辨率的时频表示，并进行时频数据融合，得到最终的时频图；

(3) 对融合后的时频图进行时频脊线旋转匹配，获得待测信号的时间中心；

(4) 利用获得的参数信息结合时域重采样技术对原始信号进行多普勒校正，得到校正后的信号；

(5) 对校正后的信号进行频域分析，从而得到相关诊断结果。

由于本文工作重点在第(2)至第(4)步，省略(1)、(5)后得出流程图如图5所示。

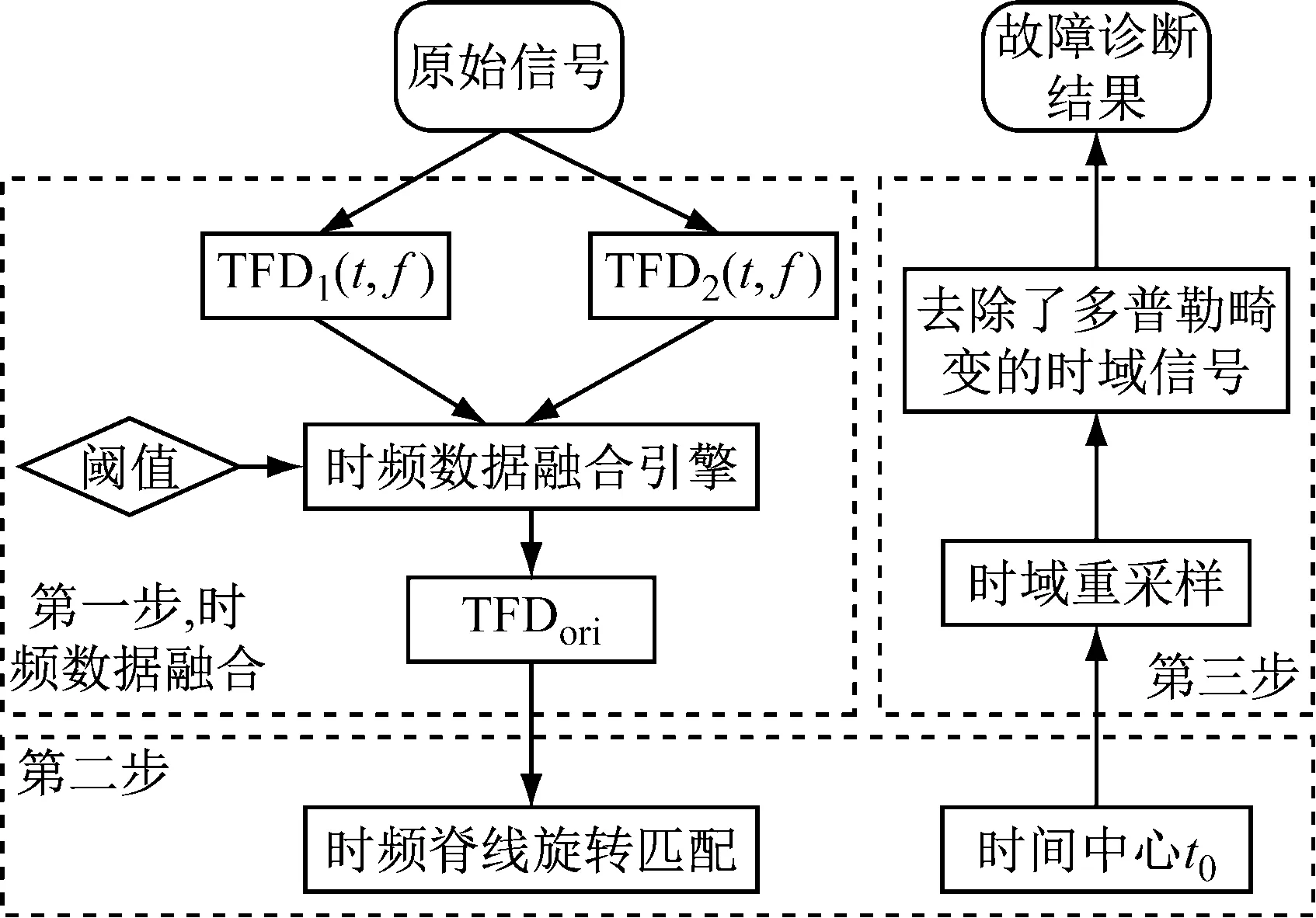
图5 本文方法核心部分流程图

3.2正弦仿真信号的校正分析

为了说明本方法的可行性，构造了一个正弦仿真信号，参数如下：r=2 m,S=4 m和v=20 m/s。声源信号为频率为1 000 Hz、幅值为1的正弦信号：

s0(t)=sin(2π×1 000t)

(7)

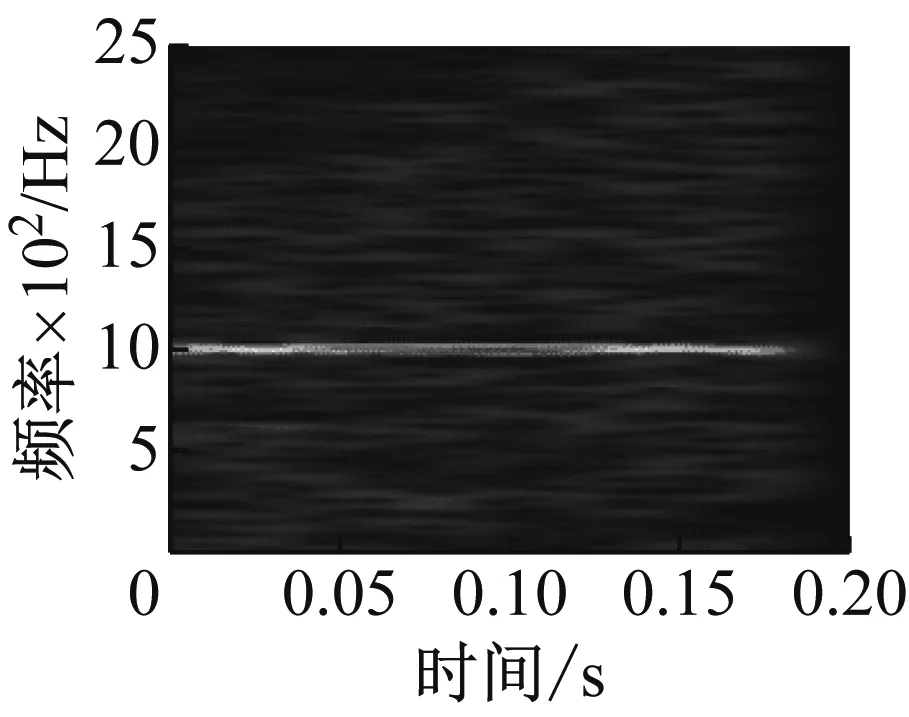
通过式(1)可得到多普勒畸变信号s(t)(采样频率fs=4 kHz)，其时域波形及频谱如图6(a)、(b)所示。可以看到频谱明显展宽，原始频率已经无法分辨。分别采用窗宽为127和511的Hamming窗对其做STFT得到时频表示如图2所示，进行时频数据融合得到图6(c)所示的时频表示。

显然，原始信号得到了很好地校正，在频域中表现为频带集中，这为后续步骤的处理带来了极大便利。

3.3冲击仿真信号的校正分析

在实际的轴承故障诊断过程中，故障信号常表现为一系列冲击对高频载波信号进行调制。这里选取单边衰减信号作为轴承故障信号的模拟：

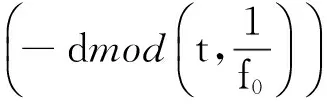
s0(t)=Asin(2πfmt)×exp (8)

(e) 多普勒校正后时频图

其中mod表示取余函数，用来产生周期性冲击。A=1表示幅值，fm=1 000 Hz表示轴承的共振频率即载波频率，d=600表示衰减速度，f0=200 Hz为故障频率。其余参数为：r=2 m,S=4 m和v=40 m/s。通过莫斯声学理论将s0(t)多普勒化后得到信号s(t)。s0(t)、s(t)及其各自包络谱如图7所示，多普勒效应导致冲击信号频带出现扩展，包络谱中已无法有效识别冲击频率。

在s(t)中加入标准差为0.45的随机噪声，加噪信号时域波形及包络谱如图8(a)、(b)所示。执行时频融合后的时频表示如图8(c)所示。

对融合时频图进行时频脊线旋转匹配，得到时间中心t0=0.1 s,与理论值S/v=0.1 s一致，根据这些参数获得重采样序列，对原始信号插值校正后得到的时频图以及包络谱如图8(c)所示。可以看出多普勒信号得到了很好地校正，同时故障频率也能很明显地识别出来。

4 道旁轴承故障实验信号分析

为进一步验证本方法的有效性，本文对列车滚动轴承的多普勒试验信号进行处理。轴承型号为NJ(P)3226XI，是我国列车广泛使用的型号，其参数如表1所示。

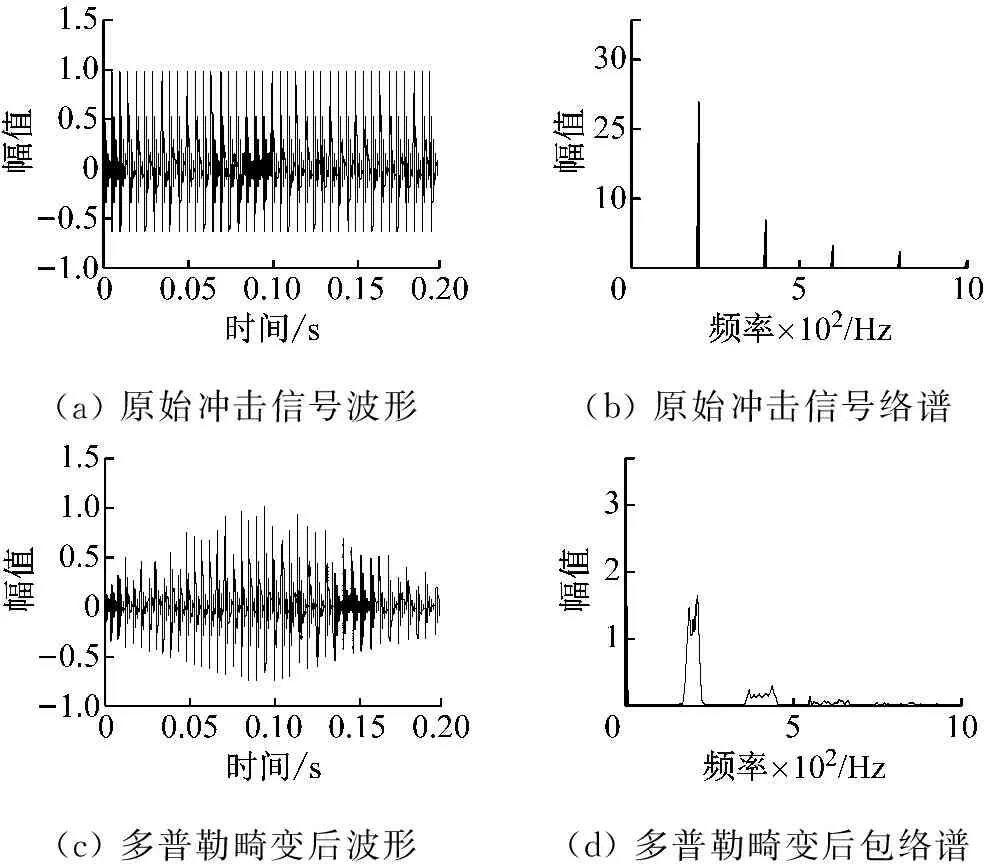
(a)原始冲击信号波形(b)原始冲击信号络谱(c)多普勒畸变后波形(d)多普勒畸变后包络谱

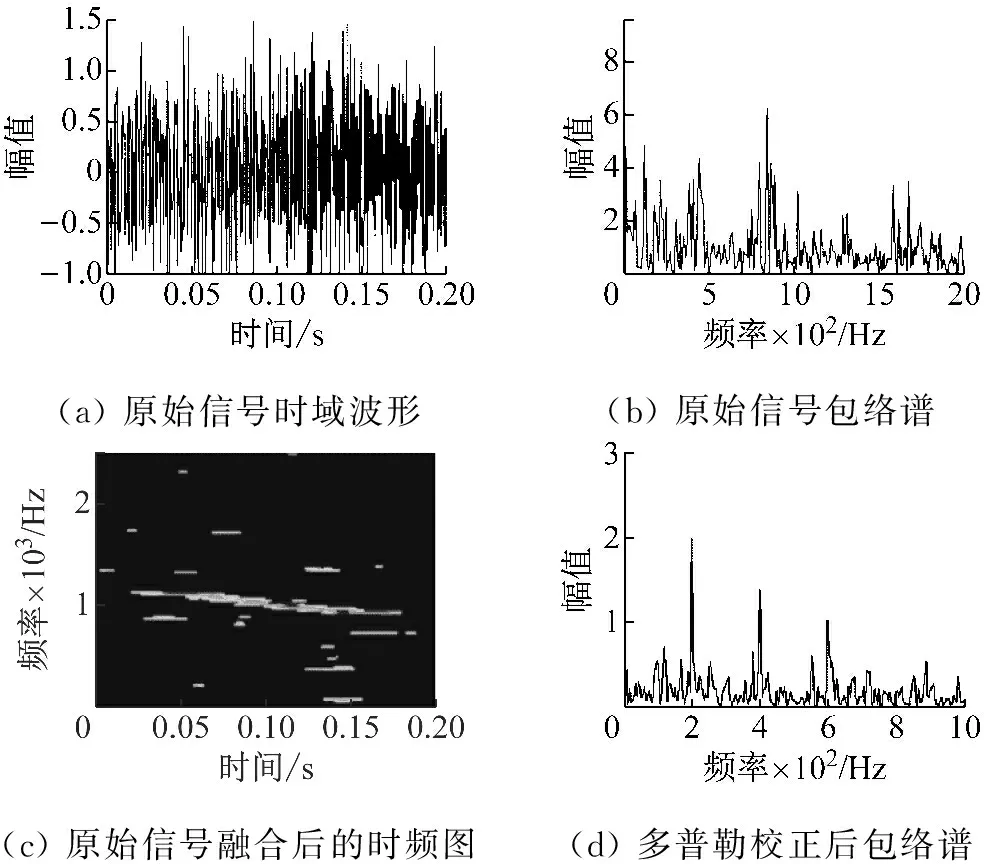
图7 冲击仿真信号

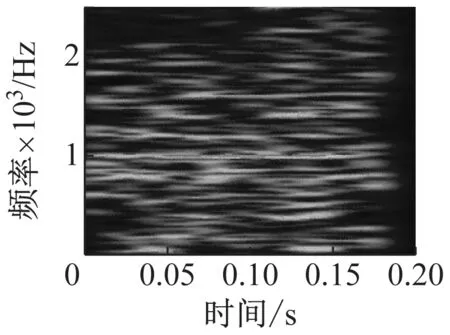
(e) 多普勒校正后时频图

型号外径/mm内径/mm结圆直径/mm滚珠直径/mm滚子数量NJ(P)3226X12501301903214

实验主要包括以下两部分:① 基于自行搭建的专用于该种型号轴承的实验平台如图9(c)所示，麦克风使用的是丹麦BK公司的4944-A，采集卡使用美国NI公司生产的PXI-4472信号采集卡，采集箱为NI公司的PXI-1033机箱。轴承故障由线切割产生，切缝为0.18 mm，位于轴承内外圈上。实验中将电机转速置为1 430 r/min，载荷为3 t，采样频率达到50 kHz，从而得到了含有轴承故障的声学静态信号；② 将采集到的静态声学信号通过音箱播放出来，同时将音箱放在汽车上，驾驶汽车以30m/s的速度直线通过麦克风(距离汽车行驶路线约2 m)，整个装置如图9(d)所示。

(a)外圈故障(b)内圈故障(c)列车轴承实验平台(d)多普勒实验场景

图9 实验信号获取

Fig.9 Experimental signal acquisition

这样我们就获得了产生多普勒畸变的轴承故障信号，后面我们将对其进行校正并提取故障信息。

另外利用表1中的轴承参数，我们可以算出轴承内外圈故障频率理论值为194.9 Hz及138.7 Hz。

4.1轴承外圈故障诊断

存在多普勒畸变的轴承外圈故障信号时域波形和包络谱如图10(a)所示，显然，受多普勒畸变的影响，出现了频带展宽我们无法从中获得故障信息。

利用本文所提出的方法，先对时频图进行时频数据融合，得到融合后的时频表示如图10(c)，对其进行时频脊线旋转匹配得到时间中心，然后计算得出重采样序列并对原信号进行多普勒校正，最终得到校正后的信号的包络谱及时频表示如图10(d)、(e)所示。

从校正后的包络谱上我们可以清楚地看到故障频率fBPFO=136.8 Hz，与前面根据轴承故障诊断相关理论计算得出的故障特征频率进行对比，发现与外圈故障特征频率138.7 Hz比较接近，由此我们可以断定该轴承存在外圈故障。

4.2轴承内圈故障诊断

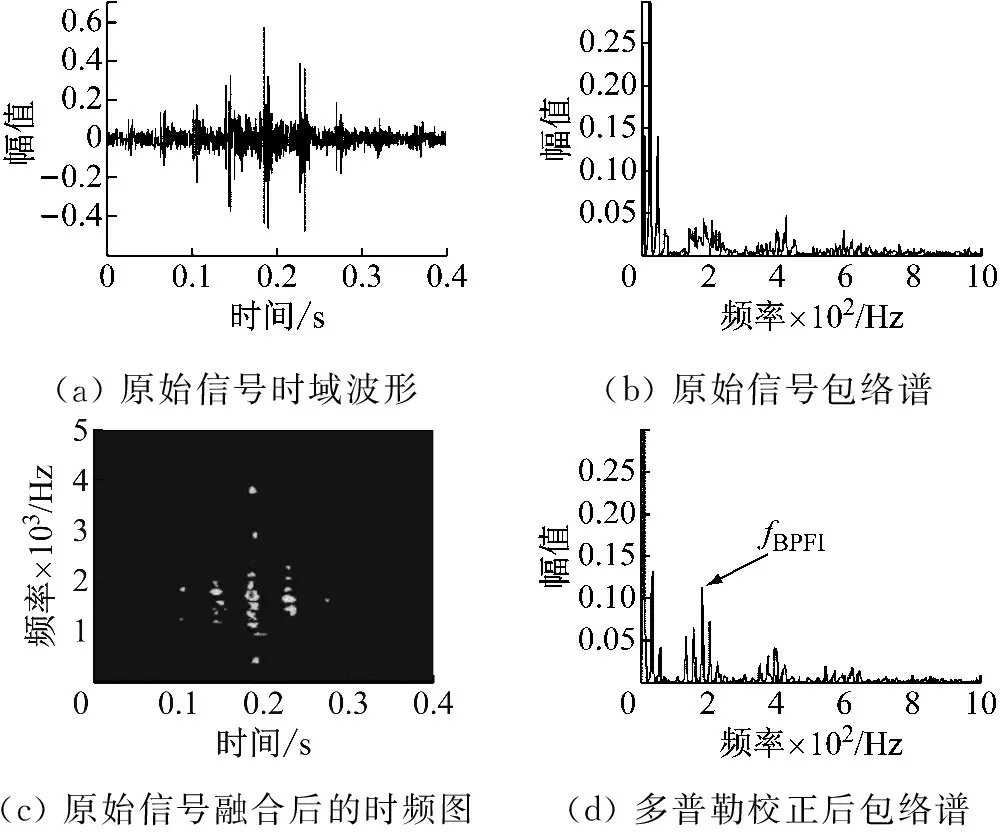
接着我们使用同样的方法对存在多普勒畸变的轴承内圈故障信号进行处理，其时域波形和包络谱如图11(a)、(b)所示，显然由于多普勒畸变的影响，故障频率已无法辨别。

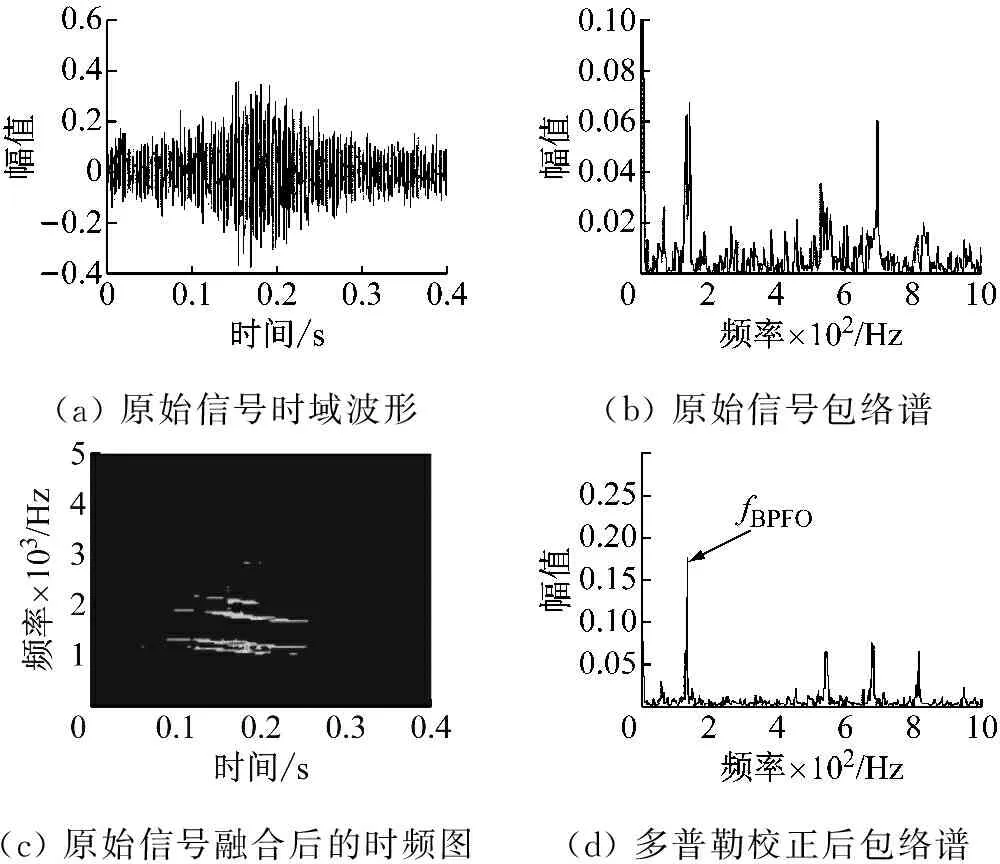
(a)原始信号时域波形(b)原始信号包络谱(c)原始信号融合后的时频图(d)多普勒校正后包络谱

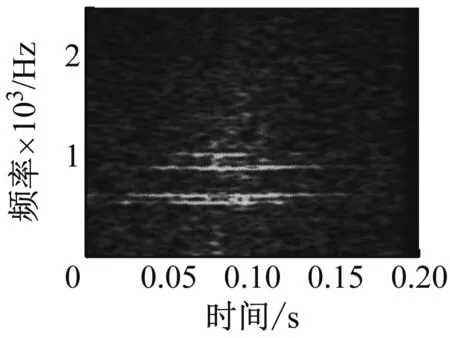
(e) 多普勒校正后时频图

(a)原始信号时域波形(b)原始信号包络谱(c)原始信号融合后的时频图(d)多普勒校正后包络谱

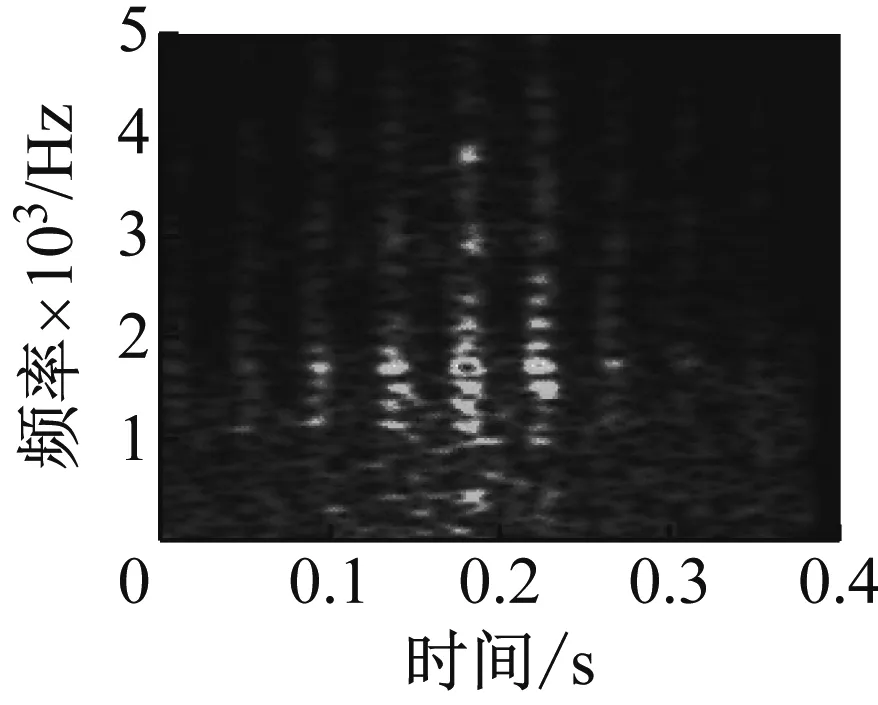
(e) 多普勒校正后时频图

利用本文所提出的方法进行处理，最终得到图11(d)、(e)所示处理结果。从校正后的包络谱上我们可以清楚地看到频率成分192.8 Hz，与前面根据轴承故障诊断相关理论计算得出的故障特征频率进行对比，发现与内圈故障特征频率194.9 Hz比较接近，由此我们可以断定该轴承存在内圈故障。

5 结 论

针对列车高速通过道旁声学诊断系统时存在多普勒效应，从而导致频带扩展、幅值调制和频移等问题，本文提出了一种基于时频脊线旋转匹配的方法，对融合后的时频图进行旋转匹配，获得了时间中心，利用它进行时域重采样成功校正了多普勒畸变，为进一步对列车轴承故障进行诊断提供了必要条件。仿真信号和实验信号的分析结果对故障信号的准确判断表明，该方法对这类多普勒畸变故障信号的校正和诊断有一定的可行性。

[1] TANDON N, CHOUDHURY A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings[J]. Tribology International, 1999, 32 (8): 469-480.

[2] HE Q, WANG J, HU F, et al. Wayside acoustic diagnosis of defective train bearings based on signal resampling and information enhancement[J]. Journal of Sound and Vibration, 2013, 332 (21): 5635-5649.

[3] 朱军, 闵祥敏, 孔凡让, 等. 基于分量筛选奇异值分解的滚动轴承故障诊断方法研究[J]. 振动与冲击, 2015, 34 (20): 61-65.

ZHU Jun, MIN Xiangmin, KONG Fanrang, et al. Rolling bearing fault diagnosis based on component screening singular value decomposition[J]. Journal of Vibration and Shock, 2015, 34(20): 61-65.

[4] HU Z, WANG C, ZHU J, et al. Bearing fault diagnosis based on an improved morphological filter[J]. Measurement, 2016, 80: 163-178.

[5] IRANI F D,吴朝院. 先进道旁车辆状态监视系统的开发和应用[J]. 国外铁道车辆, 2002, 39 (2): 39-45.

IRANI F D, WU Chaoyuan. Development and deployment of advanced wayside condition monitoring systems[J]. Foreign Rolling Stock, 2002, 39(2): 39-45.

[6] WANG C, KONG F, HE Q, et al. Doppler Effect removal based on instantaneous frequency estimation and time domain re-sampling for wayside acoustic defective bearing detector system[J]. Measurement, 2014, 50: 346-355.

[7] BARKE D, CHIU K W. Structural health monitoring in the railway industry: A review[J]. Structural Health Monitoring, 2005, 4 (1): 81-94.

[8] DYBALA J, RADKOWSKI S. Reduction of Doppler effect for the needs of wayside condition monitoring system of railway vehicles[J]. Mechanical Systems and Signal Processing, 2013, 38 (1): 125-136.

[9] ZHANG A, HU F, HE Q, et al. Doppler shift removal based on instantaneous frequency estimation for wayside fault diagnosis of train bearings[J]. Journal of Vibration and Acoustics, 2014, 136 (2): 021019.

[10] ZHANG H, ZHANG S, HE Q, et al. The doppler effect based acoustic source separation for a wayside train bearing monitoring system[J]. Journal of Sound and Vibration, 2016, 361: 307-329.

[11] 刘方, 沈长青, 何清波, 等. 基于时域多普勒校正和EEMD的列车轴承道旁声音监测故障诊断方法研究[J]. 振动与冲击, 2013, 32(24): 104-109.

LIU Fang, SHEN Changqing, HE Qingbo, et al. Wayside acoustic fault diagnosis for locomotive bearings based on Doppler effect correction and EEMD method in time domain[J]. Journal of Vibration and Shock, 2013, 32 (24): 104-109.

[12] 张翱, 胡飞, 沈长青, 等. 基于能量重心法的列车轴承多普勒畸变故障声信号校正诊断研究[J]. 振动与冲击, 2014, 33 (5): 1-7.

ZHANG Ao, HU Fei, SHEN Changqing, et al. Doppler distortion removal based on energy centrobaric method for wayside fault diagnosis of train bearing by acoustic signals[J]. Journal of Vibration and Shock, 2014, 33(5): 1-7.

[13] ZHANG H, LU S, HE Q, et al. Multi-bearing defect detection with trackside acoustic signal based on a pseudo time-frequency analysis and Dopplerlet filter[J]. Mechanical Systems and Signal Processing, 2016, 70-71: 176-200.

[14] 张海滨, 陆思良, 何清波, 等. 多普勒畸变声学信号的伪时频分析及其校正[J]. 振动与冲击, 2016, 35 (5): 14-20.

ZHANG Haibin, LU Siliang, HE Qingbo, et al. Fake time-frequency analysis of acoustic signals with Doppler distortion and its correction[J]. Journal of Vibration and Shock, 2016, 35 (5): 14-20.

[15] PENG Z K, ZHANG W M, LANG Z Q, et al. Time-frequency data fusion technique with application to vibration signal analysis[J]. Mechanical Systems and Signal Processing, 2012, 29: 164-173.

[16] MORSE P M, INGARD K U. Theoretical Acoustic (Section 2)[M]. New York: Princeton University Press, 1968.

Dopplerdistortioncorrectionmethodbasedonrotationmatchingoftime-frequencyridgelines

LIU Xingchen, HU Zhiyong, HE Qingbo, ZHU Jun

(Department of Precision Machinery and Precision Instrumentation, University of Science and Technology of China, Hefei 230027, China)

Doppler effect causes acoustic signal distortion to increase the difficulty of wayside acoustic fault diagnosis of high-speed trains. Time-domain resampling is an effective Doppler distortion correction method requiring an accurate estimation of the time center. Based on deeply analyzing variation features of instantaneous frequencies of Doppler distortion signals, a new Doppler distortion correction method was proposed. Firstly, the time-frequency fusion technique was applied to improve the resolution of time-frequency figures. Then time-frequency ridge lines were rotated and matched with the original ones to achieve the time center. Finally, the resampling sequence was utilized to correct Doppler distortion. Simulations and tests demonstrated that the proposed method can be used to effectively realize Doppler distortion correction and has a certain feasibility for the wayside acoustic fault diagnosis.

fault diagnosis; Doppler distortion; acoustic signal; rotation matching of time-frequency ridge lines

国家自然科学基金(51475441)；教育部新世纪优秀人才支持计划(NCET-13-0539)

2016-04-12 修改稿收到日期：2016-07-09

刘星辰 男，硕士，1992年7月生

何清波 男，博士，副教授，硕士生导师，1980年5月生

TH165.3; TN911.7

： A

10.13465/j.cnki.jvs.2017.17.005