结合面接触阻尼对模态耦合系统不稳定性影响

潘五九， 李小彭， 王 雪， 高建卓， 李木岩， 闻邦椿

(东北大学 机械工程与自动化学院，沈阳 110819)

结合面接触阻尼对模态耦合系统不稳定性影响

潘五九， 李小彭， 王 雪， 高建卓， 李木岩， 闻邦椿

(东北大学 机械工程与自动化学院，沈阳 110819)

针对目前结合面微观形貌对由摩擦和系统结构双重引起的模态耦合系统不稳定性影响的理论研究缺少，尝试从微观角度解释结合面的接触阻尼特性对宏观系统的影响。对车辆制动盘制动工况进行抽象综合，给出了两自由度系统的物理和数学模型，其中的接触阻尼部分采用给出的接触阻尼分形模型。分别阐释了接触阻尼比、摩擦因数、系统固有频率比及它们间的耦合效应，对系统不稳定的影响。研究方法和结果可更深入地理解结合面接触阻尼对宏观系统的影响，有一定的理论意义；同时在深入理解接触阻尼对系统不稳定的影响下可逆向反推来加工制造合适的结合面参数(分形维数D和分形尺度系数G)。

结合面；分形理论；接触阻尼；模态耦合；不稳定

机械结合面间的振动与噪声现象广泛存在于各类机械系统中。较典型并引起人们关注的振动噪声现象：刹车制动系统中的振动噪声[1]及火车在曲线轨道上行驶产生的振动、尖叫[2-3]。此类振动噪声不仅严重影响机械系统工作的稳定性，同时噪声对人居环境也造成了污染。因此，学术界和企业界一直试图弄清结合面上的振动噪声机理。对于机械结合面上的振动噪声产生的机理研究，目前来说主要有四种典型机理。分别为黏滑理论[4]，摩擦力与相对速度负斜率机制[5]，自锁滑动理论[6]和更为重要的模态耦合理论[7]。

模态耦合的系统，往往是由于本身结构因素或摩擦引起的系统矩阵不对称，而导致系统不稳定，进而产生振动噪声现象。对于模态耦合不稳定系统的研究，大多数停留在系统本身宏观结构参数对系统的影响，很少涉及从结合面微观形貌接触建模的角度，即对结合面间接触阻尼特性进行准确建模，来研究其对整个系统的影响。

另外从机械结合面的观点去研究机械系统，国内外的研究者已通过试验表明了结合面的接触形貌确实能对系统的不稳定振动噪声产生重要影响。Chen等[8]通过对相对运动的结合面试验研究指出，两种不同频率的振动噪声产生与改变相互滑动界面的粗糙度有关。Eriksson等[9]通过试验表明了车辆制动盘的表面形貌和制动噪声间有着重要的关系。Sherif[10]同样对刹车盘间的结合面形貌与不稳定系统噪声产生间的关系进行了阐释。Eadie等[11]通过分析，对车轮和车轨间的结合面形貌进行适当的加工修整，或可减小结合面间的噪声。李小彭等[12]考虑了组合梁结合面的非线性特性并对其进行预应力模态分析，试验表明了结合面特性对梁各阶振动频率有影响；并针对机床刀具切削颤振现象[13]，建立了切削结合面上含Stribeck摩擦模型的单自由度自激振动系统，研究了宏观结构参数对系统不稳定分岔特性的影响。

鉴于以上文献很多从试验角度表明机械结合面的微观接触形貌对系统稳定与否(系统若不稳定则表现为产生振动噪声现象)有着非常重要的影响，而接触形貌对系统的影响本质上又主要表现为结合面的接触阻尼和接触刚度对系统动力学的影响；且文献中几乎未涉及到从微观接触理论角度，即基于分形理论对模态耦合系统的结合面接触阻尼建模，而后分析接触阻尼对系统的不稳定性影响。因此本文的研究目标是从理论上深入地阐释结合面接触阻尼比、摩擦因数、及接触阻尼比与摩擦因数、系统固有频率比间相互耦合对系统不稳定的影响。

1 模型建立

为了研究结合面接触阻尼对系统不稳定性的影响，基于一刹车制动盘抽象出的典型模态耦合模型，改进并建立了考虑微观接触形貌特性对宏观系统影响的两自由度干摩擦振动系统，如图1所示。

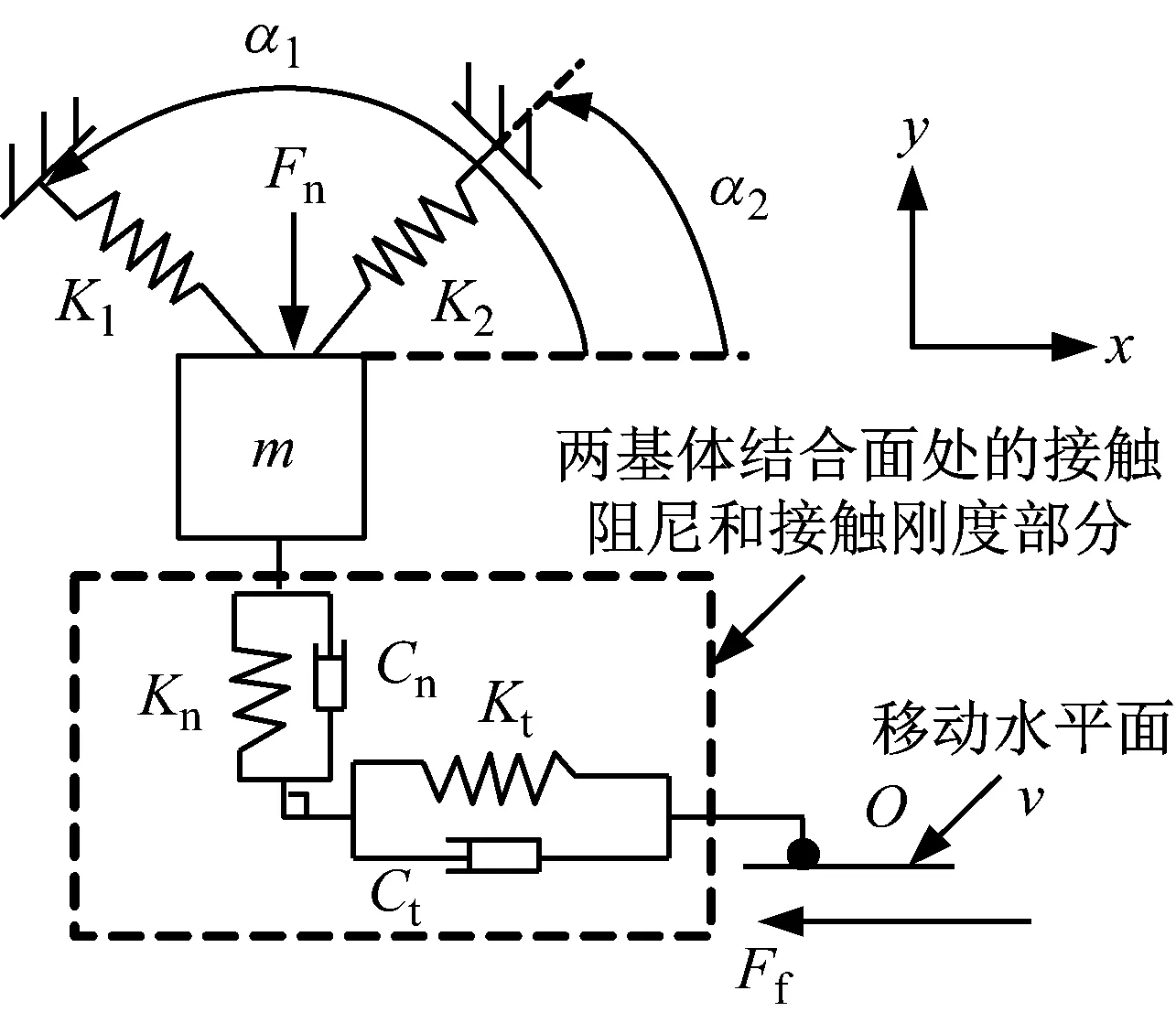
图1 两自由度模型

图1中k1和k2各自表示系统的两根线性弹簧刚度系数；倾角α1和α2的范围均属于[0°,180°]；m表示集中质点的质量；质量m和移动的水平面间的接触面构成两基体的结合面，其间的法向和切向接触刚度分别为kn和kt；Cn和Ct分别表示结合面的法向和切向阻尼；点O表示接触点；摩擦因数表示为μ；移动平面速度为ν；施加向下的法向力Fn，以使得质点m和移动平面在点O处始终处于接触状态；Ff表示点O处的摩擦力。

图1中两基体结合面接触部分的切向接触阻尼(Ct)和法向接触阻尼 (Cn)是基于分形接触理论建立的。对于基于分形理论的结合面接触阻尼建模已有较多学者做过很多有价值的研究，如张学良等[14-15]基于MB分形修正模型给出了切向和法向接触阻尼模型；田红亮等[16-17]基于修正几何分形理论和赫兹接触理论，给出了法向接触阻尼模型；从考虑摩擦因素影响的角度也同样建立了切向[18]和法向[19]接触阻尼模型。较为准确的结合面接触阻尼建模，不仅为理论上建立完善的振动模型提供依据，同时为工程上逆向设计和制造合理的结合面接触形貌(分形维数D和分形尺度系数G)来减小振动噪声提供参考。

由于本文的重点是分析结合面接触阻尼特性对模态耦合不稳定系统的影响,对于前期的切向、法向接触阻尼建模部分已完成,有兴趣的读者可参考文献[18-19]。现直接给出其最终公式。

结合面切向接触阻尼为

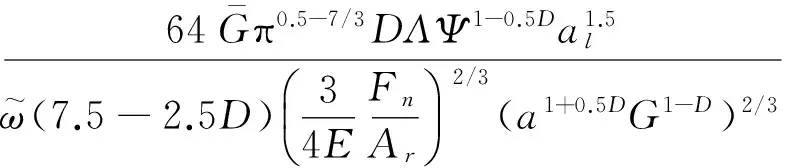
(1)

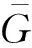
结合面法向接触阻尼为

(2)

式中：k定义为k=H/σy；H表示材料硬度；σy表示材料屈服强度；φ=σy/E；ac表示微凸体临界接触面积；Cc为临界阻尼系数可由振动测试获得；其它未注参数同上。

由式(1)和式(2)知，决定结合面形貌有两个最重要的表征参数，即分形维数D和分形尺度系数G。D越大表示结合面形貌越光滑，G越大表示结合面形貌越粗糙。

那么根据图1所示系统及给出的切向、法向接触阻尼模型，可得系统的动力学方程为

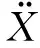
(3)

式中：

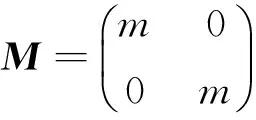
K11=k1cos2α1+k2cos2α2+kt；

K12=K21=k1sinα1cosα1+k2sinα2cosα2；

K22=k1sin2α1+k2sin2α2+kn。

Ff为结合面处的摩擦力，可由完整的库伦摩擦模型表示为

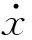
(4)

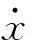
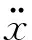
(5)

以静平衡点作为新的坐标原点，设x′=x-x0,y′=y-y0，代入式(3)为

(6)

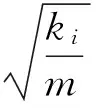
2 接触阻尼对模态耦合不稳定系统的影响

至此将详细研究结合面接触阻尼对系统不稳定特性的影响。以期能在所给的两自由度模态耦合系统中捕获更多由接触参数引起的系统动力学行为，从而为更深入地阐释接触阻尼对系统不稳定性演变历程的影响。

2.1结合面接触阻尼比ξ的影响

取参数时会确定结合面法向接触刚度值及其切向与法向的刚度比，来研究接触阻尼比对系统的影响。取m=1 kg，ω1=2 000πrad/s，ω2=1 500πrad/s，α1=180°，α2=135°，Kn=4×108N/m，切向与法向刚度比κ=0.6，Cn=30πN·s/m，以接触阻尼比ξ(切向接触阻尼与法向接触阻尼的比值)分别取0.3，0.6和1时，来研究结合面接触阻尼比ξ对系统的影响，如图2所示。由图2(a)知，两个单独分开的模态频率随着摩擦因数μ的增大，而逐渐接近，然后合并变成耦合模态。当阻尼比为0.3和0.6时，其模态呈现出不完美合并[20]。合并所对应的临界摩擦因数点μ0(超过μ0点系统会不稳定，进而可能引发噪声现象)对应于图2(b)中的Hopf分岔点，这点过后随着摩擦因数的增大，图中系统特征值实部大于0的部分表示系统会出现不稳定状态。将临界摩擦因数μ0看作控制参数，综合图2(a)和(b)知，随着结合面阻尼比的增大(此处确定了法向接触阻尼，即切向接触阻尼在增大；那么由式(1)内D，G参数的数值仿真知，对应结合面在较小的分形维数D和较大的分形尺度系数G时，得结合面阻尼比较大)，Hopf分岔点逐渐延后。

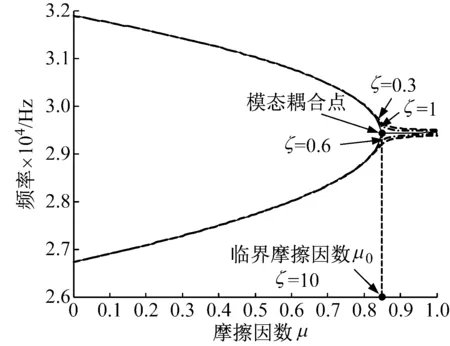
(a) 摩擦因数与特征频率

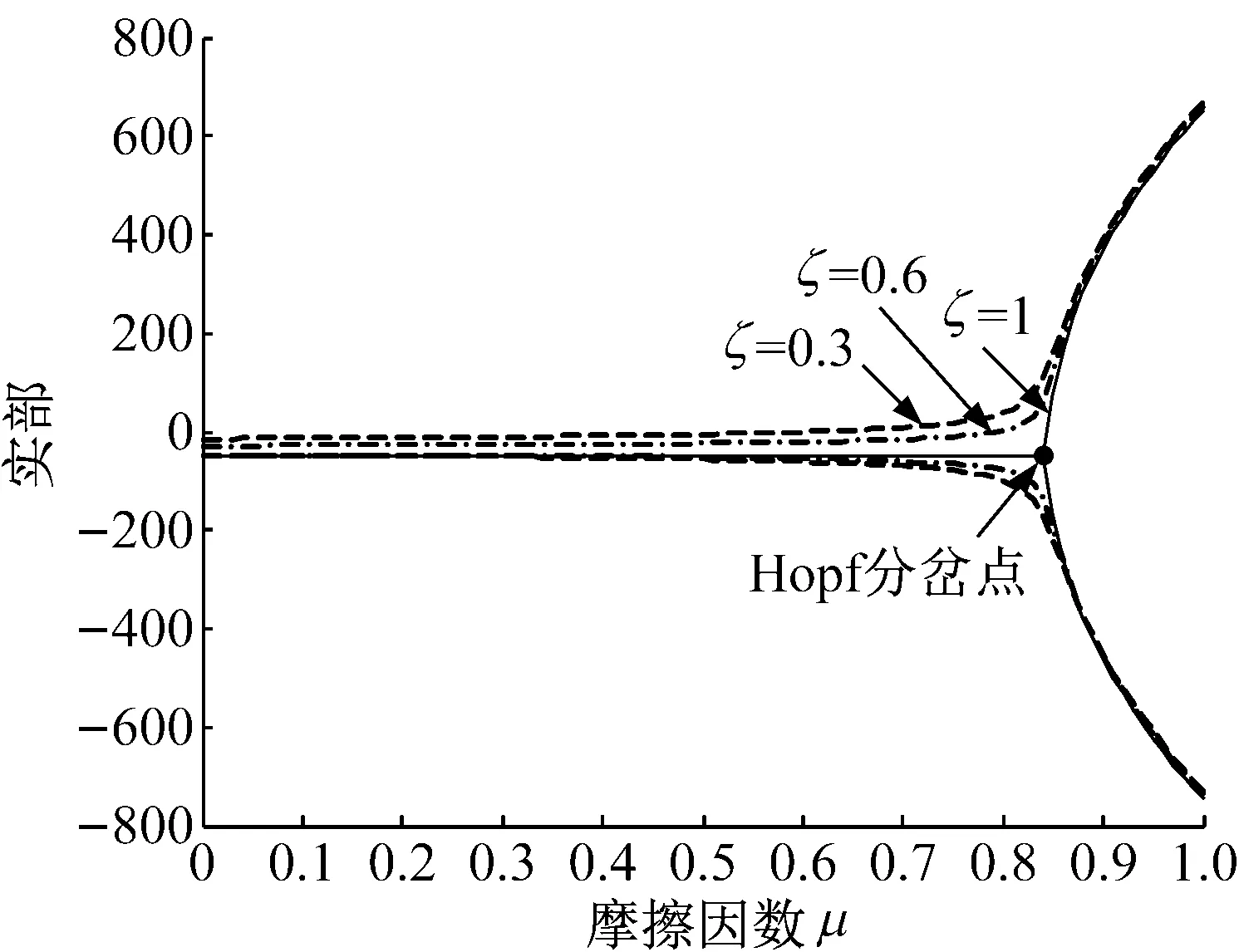
(b) 摩擦因数与特征实部

Fig.2 The relationship between the coefficient of friction and the frequency, real part under different contact damping ratio

2.2结合面接触阻尼比ξ和摩擦因数μ的耦合影响

取参数同2.1节，并依据方程(6)的齐次形式，来分析接触阻尼比和摩擦因数共同耦合下对系统不稳定性的影响。如图3所示。图3(a)、(c)和图3(b)、(d)分别表示系统特征实部和特征频率相对于摩擦因数，结合面阻尼比的变化规律图。其中图3(c)、(d)的法向接触阻尼为图3(a)、(b)的5倍。图3(a)、(c)的三维特征实部图中，实部大于0的部分为不稳定区域(反之为稳定区域)，它的不稳定增长率将表现为随时间成指数级增长；不稳定增长区对应于特征频率图的模态频率合并区。由图3(b)、(d)看出，两层分开的系统固有频率中下面一层是一阶固有频率，上面一层是二阶固有频率，且随着摩擦因数和结合面接触阻尼比的增大，两层逐渐靠近后合并，其中(d)表现为不完美合并[20]。增大法向阻尼不仅会减小Hopf分岔点的临界μ0值，而且会加大不完美合并趋势。模态频率随着摩擦因数和结合面阻尼比(在一定的法向阻尼下，即切向阻尼增大)的增大，呈现出由不完美合并至完全合并的趋势。

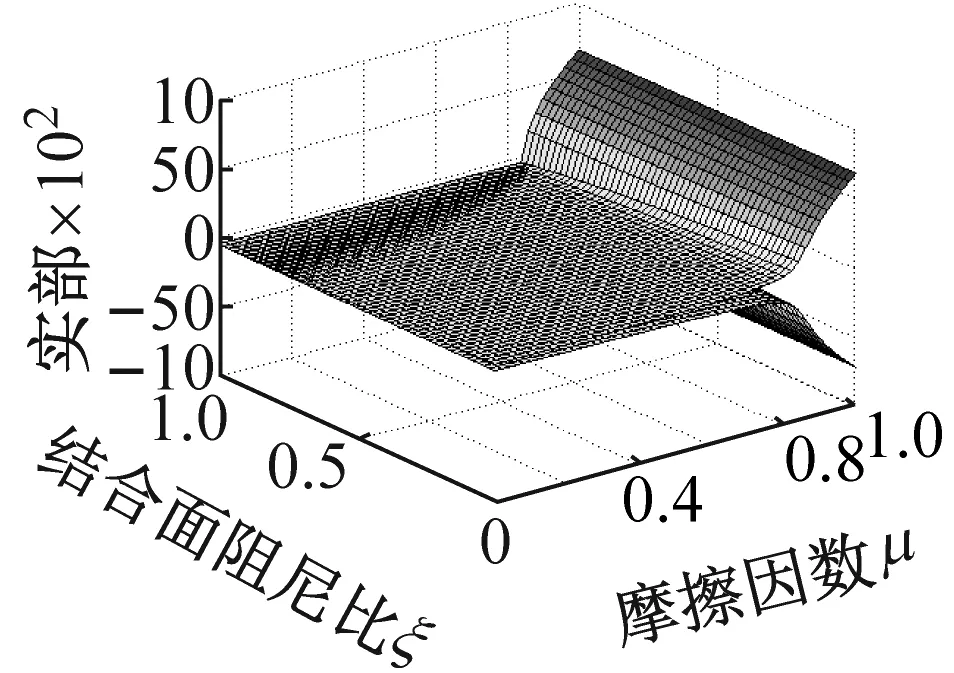
(a) 摩擦因数，阻尼比与

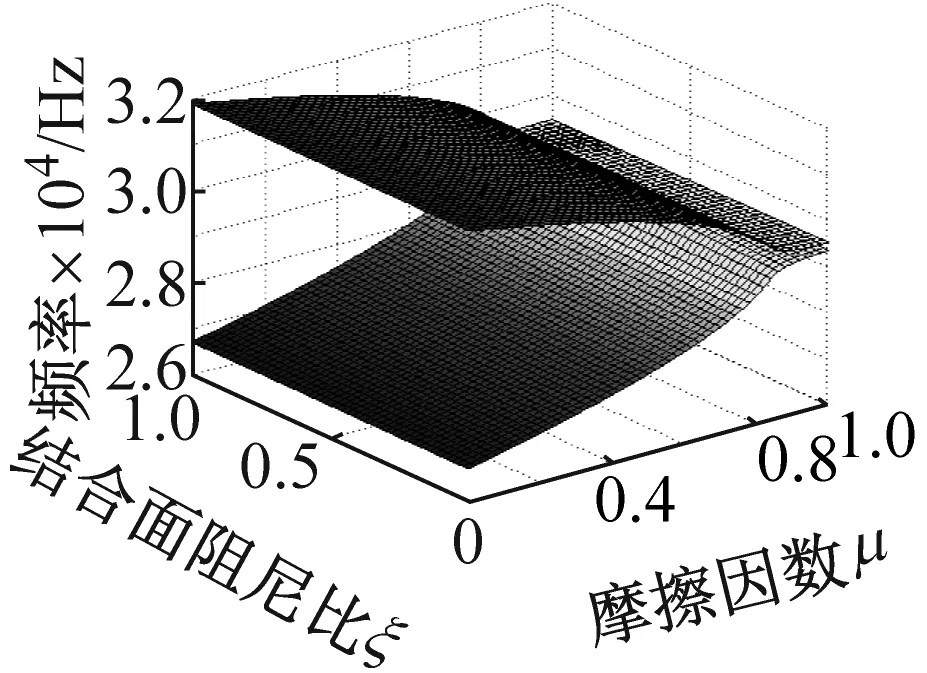
(b) 摩擦因数，阻尼比

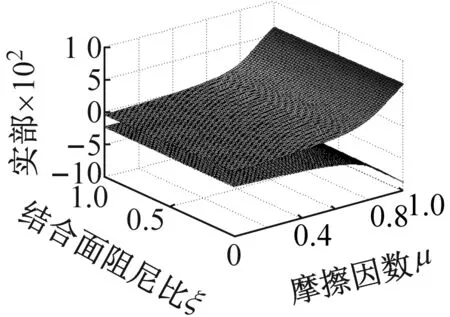
(c) 摩擦因数，阻尼比与

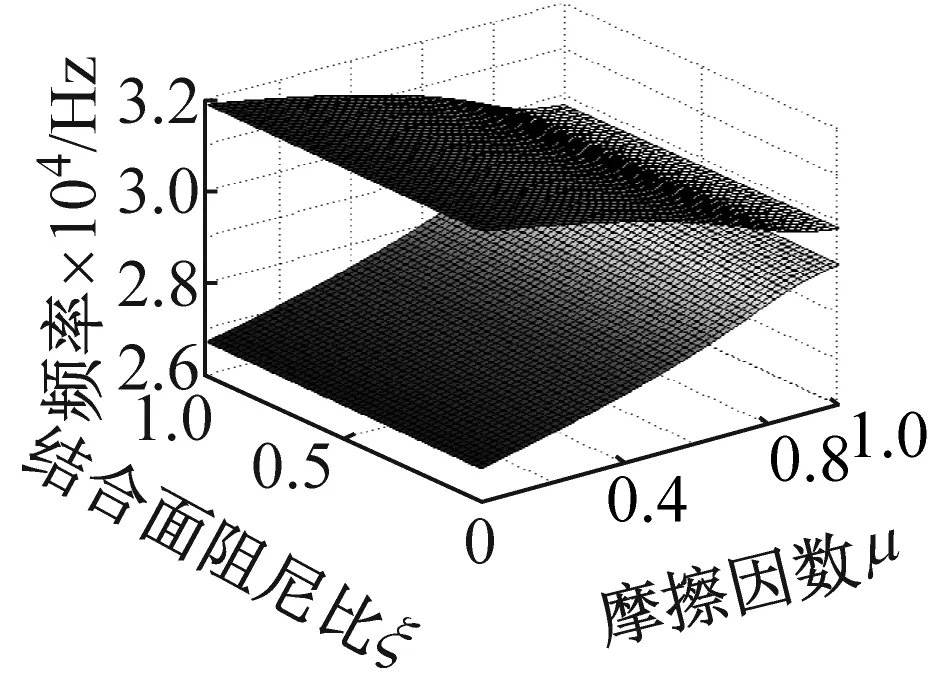
(d) 摩擦因数，阻尼比与

2.3结合面接触阻尼比ξ和系统固有频率ω的耦合影响

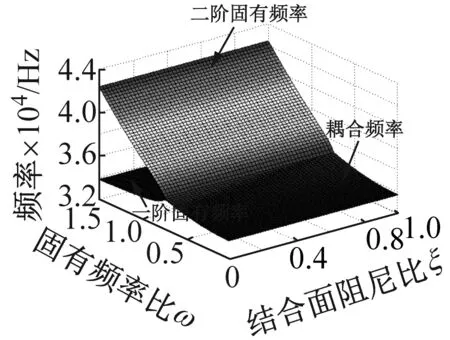
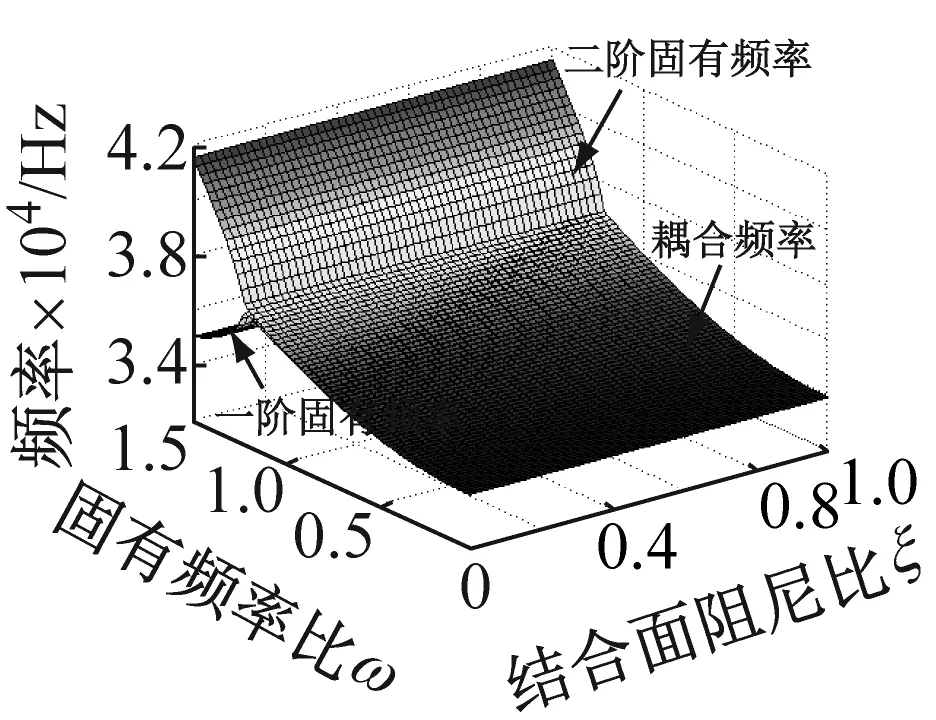
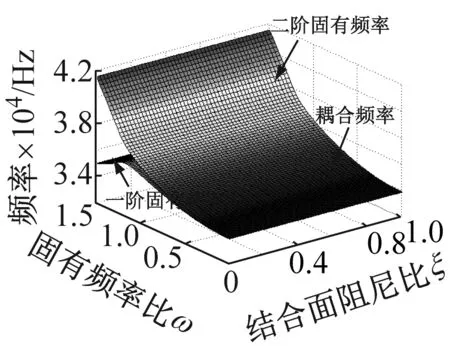
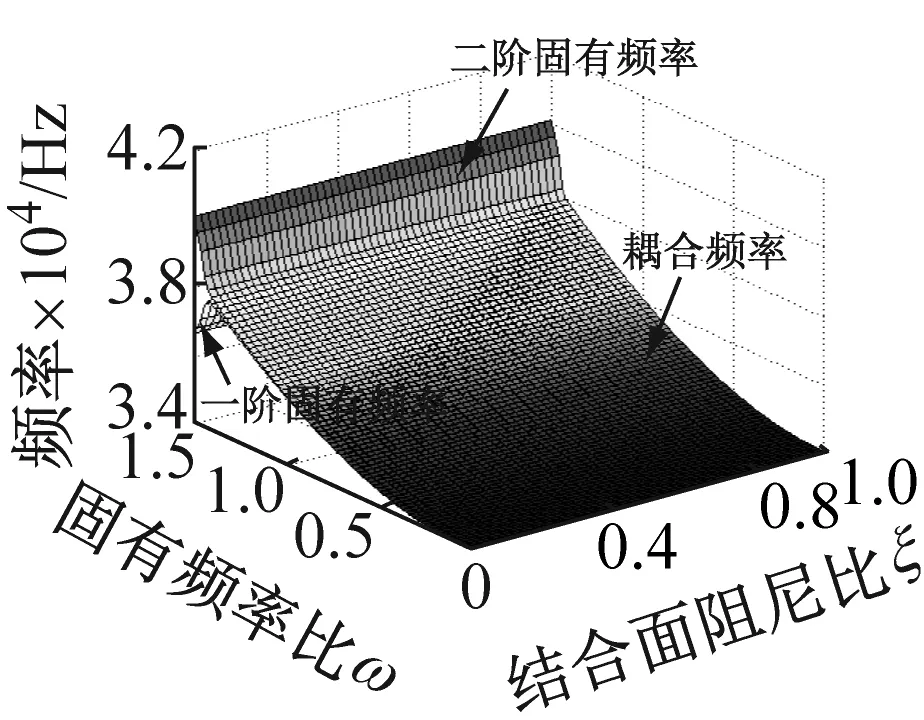
依据方程(6)的齐次形式，考虑接触阻尼比和系统固有频率的耦合效应对系统在不同摩擦因数和法向接触阻尼下的影响。图4和图5是系统特征值实部和虚部分别相对于结合面阻尼比和固有频率比ω=ω1/ω2在可变摩擦因数和法向阻尼下的变化关系，其中图4(c)和图5(c)中的法向阻尼取为图4(a)、 (b) 和(d)，图5(a)、 (b) 和(d)的10倍，来研究结合面法向阻尼增大所带来系统不稳定区的变化。由图4(a)、(b)和(d)可知，当结合面法向阻尼保持Cn=30πN·s/m不变时，系统的不稳定区域随着摩擦因数的增大而增大。图4(a)和(c)知，当摩擦因数和法向阻尼均增大时，不稳定区域同样增大。图4(b)和(c)知，保持摩擦因数不变,单纯增大法向阻尼也会增大不稳定区和造成不完美合并。从图4的四副图中也阐明了由系统结构参数决定的固有频率比和由微观接触形貌特性决定的结合面接触阻尼比的关系，即确定结合面阻尼比，较小的系统固有频率比下系统易于出现不稳定。以上这些变化过程充分说明了系统特征实部相对于结合面阻尼比和固有频率比在可变摩擦因数和法向阻尼条件下，有着多样的演变历程。图5是一一对应于图4的系统频率变化情况。从图5知，确定阻尼比，较小的固有频率下即可得耦合频率；而且图5的四副图中系统的耦合频率随着固有频率比和接触阻尼比的增大(即结合面具较小的分形维数D和较大的分形尺度系数G下)而增大。

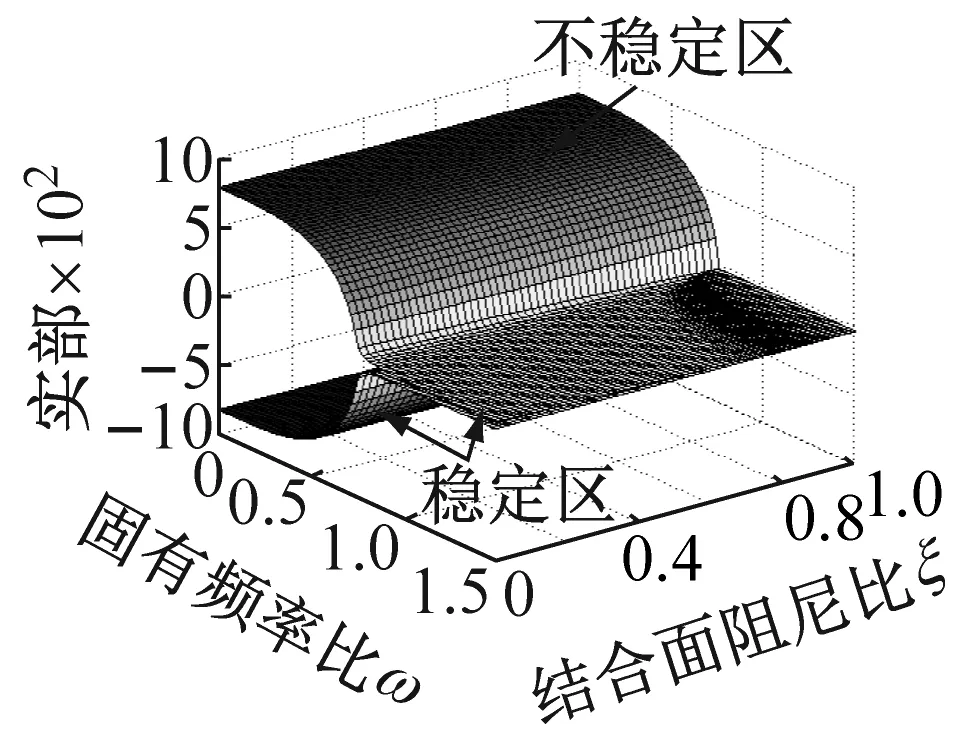
(a) μ=0.2,Cn=30πN·s/m

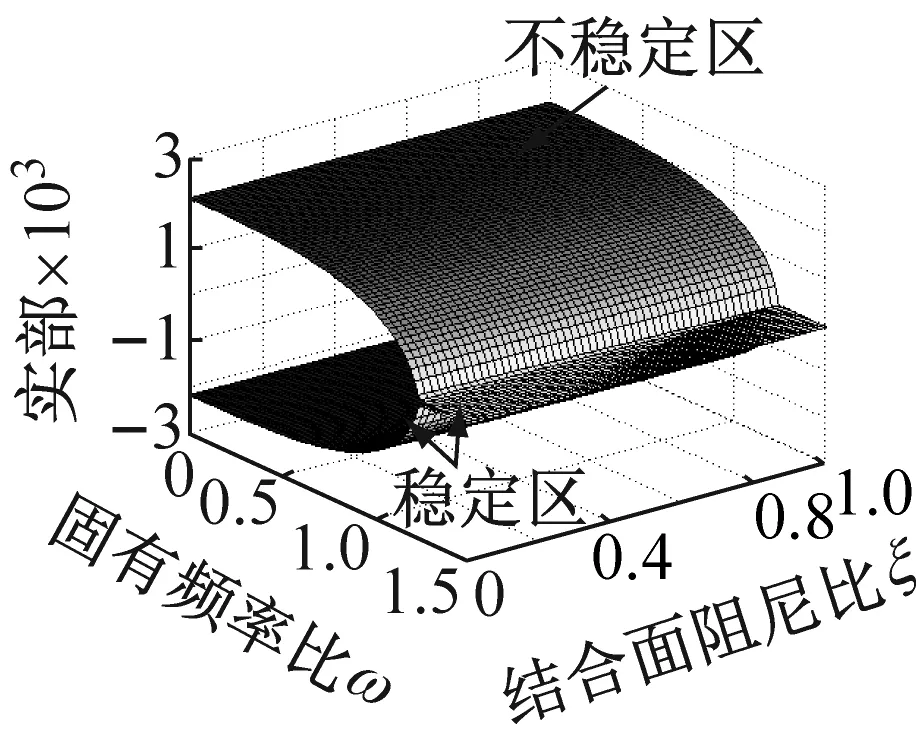
(b) μ=0.5,Cn=30πN·s/m

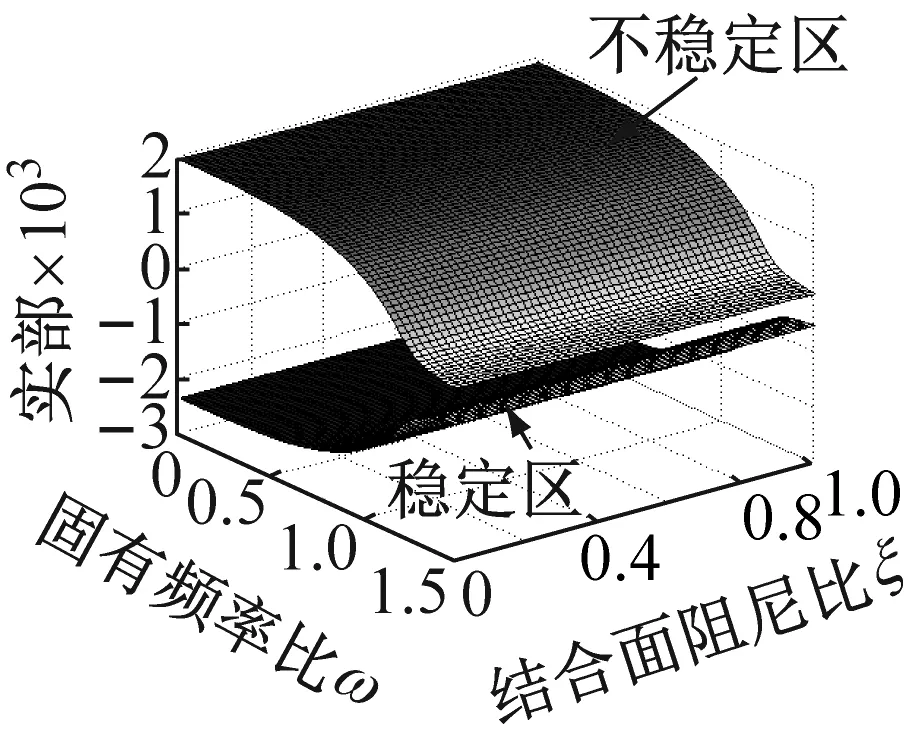
(c) μ=0.5，10倍Cn

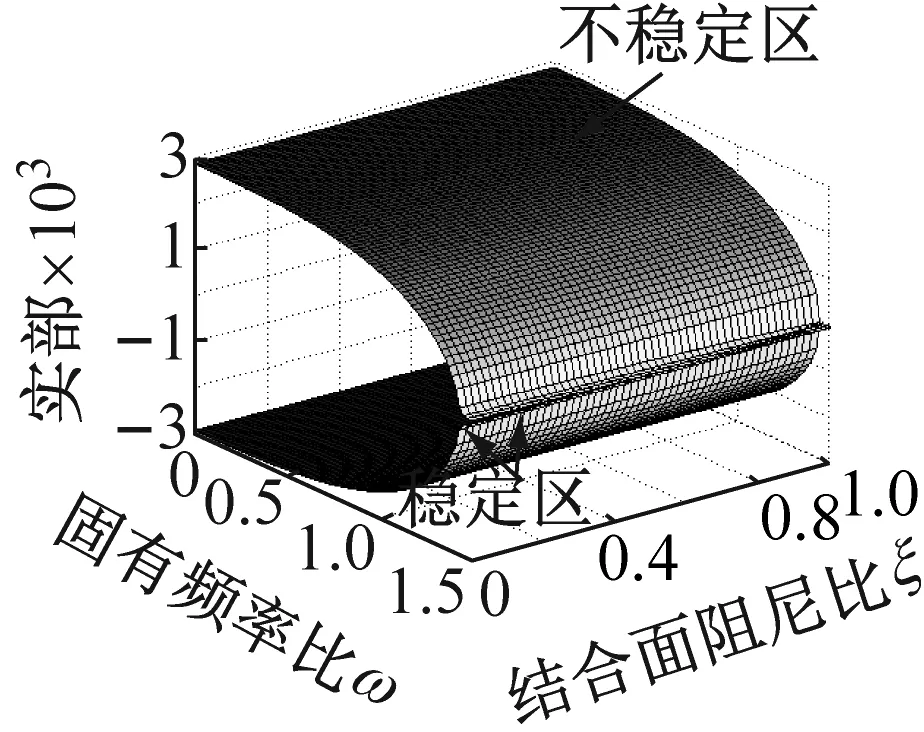
(d) μ=0.8,Cn=30πN·s/m

综上知，两个相互接触物体的结合面间不同接触阻尼状态决定了系统的稳定与否，若系统不稳定进而可能会引起振动噪声等问题的出现。这和文献[8]试验中改变相互滑动系统的结合面后的相关现象相对应。因此，两物体间的结合面形貌特性需予以特别的加工制造，进而根据前文给出的接触阻尼模型得到恰当的接触阻尼，这样或可以减小由不恰当的结合面形貌而带来的不稳定噪声。当然对于文中的此种重要的模态耦合不稳定振动噪声机制在结合面接触阻尼下的影响关系还需要更加细致地加以分析研究，还需从试验和理论上不断加以完善。

(a) μ=0.2,Cn=30πN·s/m

(b) μ=0.5,Cn=30πN·s/m

(c) μ=0.5，10倍Cn

(d) μ=0.8,Cn=30πN·s/m

3 结 论

(1) 证明区分系统稳定和不稳定的Hopf分岔点与接触阻尼密切相关。随着结合面阻尼比的增大，即对应结合面在较小的分形维数D和较大的分形尺度系数G时，Hopf分岔点逐渐延后。

(2) 系统一，二阶频率随摩擦因数和结合面接触阻尼比的增大，而逐渐合并，进而导致系统不稳定；单纯增大或同时增大摩擦因数、法向阻尼可使系统不稳定区增大；一定的结合面阻尼比，较小的系统固有频率比下系统易于出现不稳定；耦合频率随着固有频率比和接触阻尼比的增大(即在较小的分形维数D和较大的分形尺度系数G下)而增大。

(3) 基于分形理论给出切向、法向接触阻尼模型，并从结合面微观接触角度，来分析接触阻尼对宏观系统不稳定性的影响，以此来解释宏观系统相应的不稳定振动噪声现象是可行的。

[1] OUYANG O, MOTTERSHEAD J, LI W. A moving-load model for disc brake stability analysis[J]. Transactions of ASME Journal of Vibration and Acoustics, 2003,125(1):53-58.

[2] HECKL M, ABRAHAMS I. Curve squeal of train wheels, part I: mathematical model for its generations[J]. Journal of Sound and Vibration, 2000,229(3):669-693.

[3] BEER F, JANSSENS M, KOOIJMAN P. Squeal noise of rail-bound vehicles influenced by lateral contact position[J]. Journal of Sound and Vibration, 2003,267(3):497-507.

[4] IBRAHIM R. Friction-induced vibration, chatter, squeal and chaos: Part I: Mechanics of contact and friction[J]. ASME Appl. Mech. Rev, 1994,47(7):209-226.

[5] IBRAHIM R. Friction-induced vibration, chatter, squeal, and chaos, Part 2: Dynamics and modeling[J]. Applied Mechanics Review, 1994,47(7):227-253.

[6] SPURR R T. A theory of brake squeal[J]. Proceedings of the Institution of Mechanical Engineers Automobile Division, 1961, 15(1):33-52.

[7] HOFFMANN N, FISCHER M, ALLGAIER R. A minimal model for studying properties of the mode-coupling type instability in friction induced oscillations[J]. Mechanics Research Communications, 2002,29(4):197-205.

[8] CHEN G X, ZHOU Z R. Experimental observation of the initiation process of friction-induced vibration under reciprocating sliding conditions[J]. Wear, 2005, 259(1):277-281.

[9] ERIKSSON M, BERGMAN F, JACOBSON S. Surface characterization of brake pads after running under silent and squealing conditions[J]. Wear, 1999, 232(2):163-167.

[10] SHERIF H A. Investigation on effect of surface topography of pad/disc assembly on squeal generation[J]. Wear, 2004, 257(7):687-695.

[11] EADIE D T, KALOUSEK J, CHIDDICK K C. The role of high positive friction (HPF) modifier in the control of short pitch corrugations and related phenomena[J]. Wear, 2002, 253(1/2):185-192.

[12] 李小彭, 赵光辉, 杨皓天，等. 考虑结合面影响的组合梁非线性预应力模态分析[J]. 振动与冲击, 2014，33(4):17-21.

LI Xiaopeng, ZHAO Guanghui, YANG Haotiang et al. Nonlinear pre-stressed modal analysis for a composite beam considering influence of joint surface[J]. Journal of Vibration and Shock, 2014，33(4):17-21.

[13] 李小彭, 孙德华, 岳冰，等. 质量-弹簧-带摩擦自激振动系统的分岔特性及其控制研究[J]. 振动与冲击, 2015，34(15):28-32.

LI Xiaopeng, SUN Dehua, YUE Bin, et al. Bifurcation characteristics and control of a mass-spring-belt friction self-excited vibration system[J]. Journal of Vibration and Shock, 2015，34(15):28-32.

[14] ZHANG X L, WANG N S, LAN G S, et al. Tangential damping and its dissipation factor models of joint interfaces based on fractal theory with simulations[J]. Journal of Tribology, 2013, 136(1):249-256.

[15] 张学良, 丁红钦, 兰国生,等. 基于分形理论的结合面法向接触阻尼与损耗因子模型[J]. 农业机械学报, 2013, 44(6):287-294.

ZHANG Xueliang, DING Hongqin, LAN Guosheng, et al. Normal contact damping and dissipation factor model of joint interfaces based on fractal theory[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(6):287-294.

[16] 田红亮, 郑金华, 赵春华,等. 界面损耗因子与法向阻尼的计算方法[J]. 上海交通大学学报, 2015(5):687-694.

TIAN Hongliang, ZHENG Jinhua, ZHAO Chunhua, et al. Calculating method of surface dissipation factor and normal damping[J]. Journal of Shanghai Jiao Tong University, 2015(5):687-694.

[17] 田红亮, 严峥嵘, 郑金华,等. 一个新的干摩擦结合部法向接触阻尼方程[J]. 哈尔滨工业大学学报, 2016(1):133-140.

TIAN Hongliang, YAN Zhengrong, ZHENG Jinhua, et al. A novel expression of normal contact damping for dry tribology joint interface[J].Journal of Harbin Institute of Technology, 2016(1):133-140.

[18] 李小彭,王伟,赵米鹊,等.考虑摩擦因素影响的结合面切向接触阻尼分形预估模型及其仿真[J]. 机械工程学报,2012,48(23):46-50.

LI Xiaopeng, WANG Wei, ZHAO Mique, et al. Research on fractal prediction model for tangential contact damping of joint surface considering friction factors and its simulation[J]. Journal of Mechanical Engineering, 2012,48(23):46-50.

[19] LI X P, YUE B, ZHAO G H, et al. Fractal Prediction Model for Normal Contact Damping of Joint Surfaces considering Friction Factors and Its Simulation[J]. Advances in Mechanical Engineering, 2014(4):133-137.

[20] SINOU J J, FRITZ G, JEZEQUEL L. The role of damping and definition of the robust damping factor for a self-exciting mechanism with constant friction[J]. Journal of Vibration & Acoustics, 2007, 129(3):297-306.

Effectsofcontactdampingofjointsurfacesoninstabilityofamode-coupledsystem

PAN Wujiu, LI Xiaopeng, WANG Xue, GAO Jianzhuo, LI Muyan, WEN Bangchun

(School of Mechanical Engineering &Automation, Northeastern University, Shenyang 110819, China)

Aiming at lacks of theoretical study on joint surface morphology characteristics affecting the stability of a mode-coupled system caused by friction and its structure, influences of contact damping on the macro system were studied and explained from the micro-aspect. Firstly, the mathematical and physical model of a 2-DOF system was given based on the background of the vehicle brake disc where the contact damping part was described with the known contact damping fractal model. Then, influences of contact damping ratio, friction coefficient, system natural frequency ratio and their coupling effects on the instability of the system were analyzed, respectively. Finally, it was shown that the study method and results can promote more deeply understanding effects of contact damping of joint surfaces on the macro system, these effects have a certain theoretical significance; at the same time, deeply understanding the effects of contact damping on the system instability can also promote inversely deriving appropriate parameters of joint surfaces (fractal dimensionDand fractal scale coefficientG) for manufacturing.

joint surfaces; fractal theory; contact damping; mode-coupled; instability

国家自然科学基金(51275079；51575091)；中央高校基本科研业务专项资金资助(N160306003)

2016-04-21 修改稿收到日期：2016-06-15

潘五九 男，博士生，1986年生

李小彭 男，博士，教授，博士生导师，1976年生

TH113

： A

10.13465/j.cnki.jvs.2017.17.003