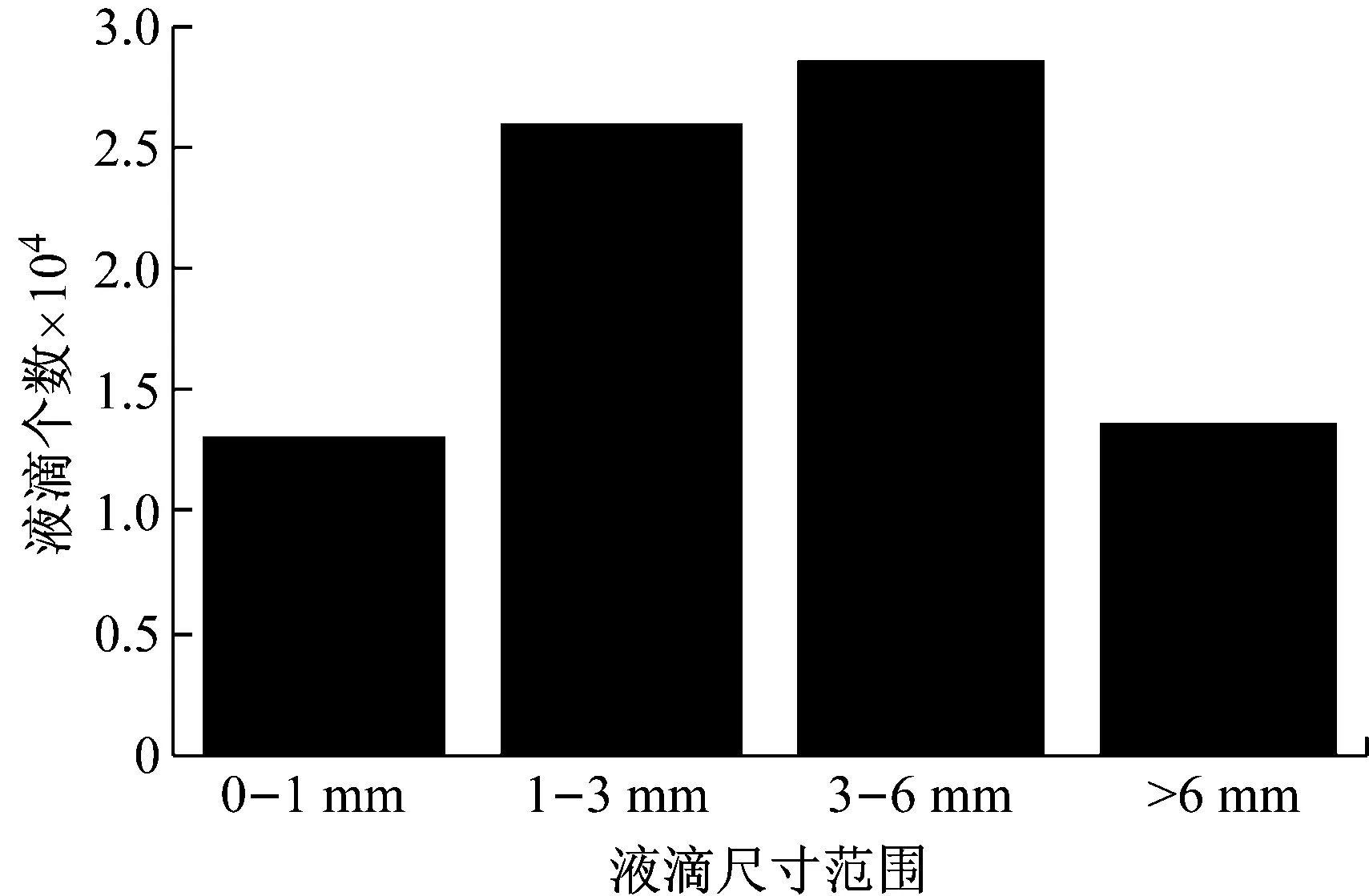
黏性液体爆炸抛撒模型
2017-09-25王红英王树山
康 凯, 马 峰, 王红英, 王树山
(1. 国民核生化灾害防护国家重点实验室, 北京 102205;2. 北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)
黏性液体爆炸抛撒模型
康 凯1,2, 马 峰2, 王红英1, 王树山2
(1. 国民核生化灾害防护国家重点实验室, 北京 102205;2. 北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)
黏性液体爆炸抛撒模型的建立对数值模拟黏性液体爆炸抛撒形成的抛撒云团过程具有重要意义。黏性液体爆炸抛撒包含液体初始驱动、空化效应产生、液体环形成、射流形成和断裂、液滴破碎等现象,这是一个复杂的物理过程。根据不同阶段、不同现象流动特征,建立牛顿黏性流体爆炸抛撒数学模型,计算得到液体抛撒速度、抛撒半径以及液滴尺寸分布。计算结果表明抛撒半径与黏度成正比,而抛撒速度衰减曲线曲率与之成反比。为验证数学模型的准确性设计试验,试验结果与结论一致,模型准确性得到验证。
黏性液体; 爆炸抛撒; 数学模型; 试验研究
黏性效应不可忽略的液体称为黏性液体。动态载荷(如爆炸)驱动下黏性液体的抛撒是一个极为复杂的液体流动过程:爆炸初期,液体被驱动,并伴随“空化”效应,继而空气出现R-T界面不稳定;界面不稳定非线性发展阶段,空气侵入黏性液体形成半径为r0的圆形气泡;同时,液体进入空气形成液体尖钉(射流),液体尖钉在惯性力和空气阻力的作用下,拉伸变细变长,这一过程中尖钉速度下降、尖钉圆顶半径变大;然后射流失稳并破碎成液滴;液滴在抛撒过程中发生二次破碎。黏性液体抛撒过程是上述几种物理现象的叠加、耦合。初始驱动完成之后,液体空化,液体环、射流以及液滴的出现、演化和破碎过程,并不能理解为一个时序上的顺序发展。因此,整个物理过程的数学化表达要紧扣液体抛撒各个阶段和现象流动特征。
Kudryashova等[1]对爆炸抛撒生成气溶胶颗粒过程的简化建模分析及实验研究,对其中炸药起爆、冲击波传播、空化发展、液滴形成和蒸发过程进行建模、计算,并给出了获得的气溶胶颗粒的尺寸分布及其蒸发情况。薛社生等[2-6]分别基于该假设对液体爆炸抛撒近场阶段进行了建模研究,发展了“液体环”断裂破碎的若干判据,例如不稳定增长判据、能量判据,给出了一维数值模拟结果,并由此给出液体首次破碎尺寸分布的模拟计算。方伟等[7]通过FAE 燃料的野外靶场抛撒试验实验研究,分析了燃料运动速度生成规律,液体介质中靠近容器壁的点A受到爆炸冲击波的直接作用,液体速度迅速增大到最大值,冲击波对A点的驱动作用持续减弱,气动阻力的作用相对增大,A点速度开始缓慢降低。以上研究皆以低黏(Oh<0.1)液体爆炸抛撒特征建立数学模型。罗琳等[8]对柴油的抛撒成雾进行实验设计与研究,分析了高黏度柴油在抛撒过程中黏度对抛撒半径产生的影响,当黏度增大后,传统的数学模型需要进行黏度参数修正,以适应黏性液体爆炸抛撒模型的有效性。
1 黏性液体爆炸抛撒模型
1.1物理过程分析
本文根据爆炸驱动黏性液体抛撒过程的流动特征,总结归纳前人针对不同特征过程研究成果,建立了用于描述黏性液体爆炸抛撒全过程的数学模型。首先以经验公式模式建立衰减系数的表达式,并以此建立基于衰减系数和黏度参量的抛撒介质速度和半径随时间变化方程;随着空化效应研究的深入,发现该效应的不可忽略性,建立无量纲表达式来推算空化量,并由能量平衡原理推算空化气泡破碎所形成的液滴尺寸;应用“液体环”理论建立液体环和液体射流初始模型,但其尖钉速度衰减方程在应用中与实际值相差较远,所以应用基于衰减系数和黏度参量的抛撒介质速度经验公式替代尖钉速度下降方程,组合成液体射流生成数学模型;由R-T不稳定推导射流在不同黏度速度时不同的断裂模式;最后,考虑黏性对液滴二次破碎的影响建立不同破碎模式的液滴尺寸分布方程。
1.2数学模型建立
液体破碎的机理十分复杂,随运动形态的变化而不同。本文所提到流体为牛顿流体,为了简化问题,做如下假设:① 液体是不可压缩理想流体;② 液体界面近似为平面;③ 流体减速度为常数。鉴于流场最大速度比声速小1个量级,环的厚度也较环半径小1个量级,则假设①和②是合理的。而第③个假设是从实验结果得到的近似。
(1) 初始阶段
在驱动阶段,影响抛撒速度的主要因素包括炸药释放的能量W、装盛液体容器的直径D、高L和壁厚d,黏性液体密度ρ和表面张力σ,其速度衰减系数ω[9]的表达式为
ω=k1Wγ1dγ2Dγ3Lγ4σγ5ργ6
(1)
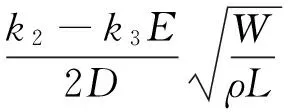
(2)
式中,umax为液体抛撒速度的最大值。
(2) 空化过程
(3) 液体环的特征
根据不可压缩R-T不稳定性理论,液体环的界面扰动增长最快的波长:
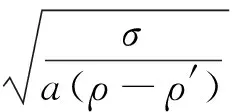
(3)
式中:a是界面减速度;ρ是液体密度;ρ′是气体密度;σ是表面张力系数。
液体环的气泡上升速度气泡相对于界面上升速度:
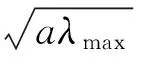
(4)
式中,γ为多维多相流体的稳定系数(2维:γ=0.23~0.29,3维:γ=0.346~0.39)。
(4) 射流速度确定和其形成
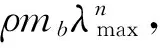
(5) 射流断裂
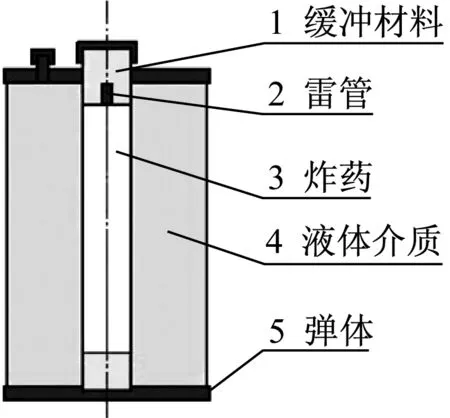
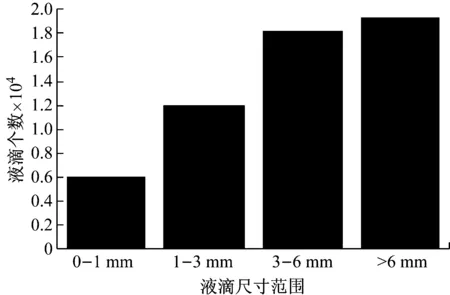
射流临界断裂值的确定:当液体Oh<0.01时,丝状射流有足够的长度时,丝状射流将形成凸起并分离成薄丝并最终分解为单独的液滴。当Oh≤0.1时,Oh和L0共同决定破碎模式。丝状射流的L0>L0c,Oh>Ohc,射流将会破碎,然而L0 (5) (6) (7) (6) 液滴破碎 (8) 以临界We数来判断液滴破碎的发生,并确定破碎后液滴的平均直径及个数。当液体黏性较小,即Oh数较小(Oh<0.1)时,按照以上结论,临界We数大约为12。当液体黏性增大,即Ohnesorge数较大时,液滴将难以破碎或者不能破碎。Corino等[13]给出了如下计算临界We数的经验公式We=12(1+1.077Oh1.6),将该式代入式(8),得到新的破碎范围。通过We范围的判断对最后液滴的尺寸分布进行估计,统计不同尺寸范围的液滴数。 (7) 抛撒半径 由经验公式得到不同时刻液体抛撤半径: (9) 但随着黏性的增加,液滴的飞散能力受黏性影响明显增大,其次液滴的表面张力、相对速度也影响这液滴的飞散能力,由于相对速度在umax中以包含,在这里引入代表黏性力与表面张力之比的Oh数对公式进行修正,伴随着抛撒半径随之变化,通过实验和经验分析,得出黏性液体抛撒半径: (10) 本小节结合经验与理论公式,修正速度方程和液滴破碎黏度参数,耦合近场驱动动力学和远场飞散动力学,获得黏性液体爆炸抛撒全过程数学模型,在下一节中对该模型的准确性进行验证。 为研究黏性液体爆炸抛撒机理与同时验证数学模型的准确性设计以下实验。 实验系统由爆炸洞、液体爆炸抛撒容器、悬挂架、照明系统、高速摄影仪、中心装药、电点火头起爆及收集系统。实验装置如图1,参数如表1。 图1 爆炸抛撒液体装置示意图 典型实验结果如图2所示。 1号工况条件装填介质为动力黏度为125 mpa·s的黏性液体,云团增长形成过程如图2。其中4幅图片的顺序为t= 2 ms、6 ms、18 ms和30 ms时刻气溶胶爆炸成形过程。图片中也展示了气溶胶云团的增长形成过程。图中显示在6 ms时刻气溶胶介质向外喷射的射流前沿才卷曲,18 ms左右云团外部才开始向上卷曲,28 ms才有翻滚涡团的特点。这表明黏性液体作为气溶胶介质的惯性较大,飞散的较远,形成的云团较大。 表1 工况设计 图2 1号工况条件下云团形态变化 以表1中序号1、3两种不同条件为输入算例,利用该模型对两状态爆炸结果进行了分析,1号工况其部分结果如图3、图4所示,3号工况其部分结果如图5、图6所示。 由图3~图6所示,计算所得的抛撒半径R-t曲线、抛撒速度v-t曲线与实测曲线对比的一致,但同时存在部分误差。由于在模型建立过程中简化了部分物理过程,包括液滴的蒸发与并聚、液体与气体界面的热传导、汽化凝固等现象,均可能是导致曲线存在误差的因素,并且误差在模型中传递会发生累积,这些简化过程的数学模型有待进一步讨论。 对比图3和图5,黏度更大的3号工况云团扩散半径在实测曲线和模拟曲线都明显大于1号工况,由此即说明了数学模型关于云团扩散半径计算的准确性,同时证明了黏度对云雾状态的影响随着时间的增长,抛撒半径与黏度成正比关系。 图3 1号工况条件下云团半径随时间变化曲线 Fig.3 The comparison chart of the measured radius changing with time curve and simulation curve (First Condition) 图4 1号工况条件下速度随时间变化曲线 黏性液体爆炸驱动过程就是压力波在黏性液体中传播的过程,在此过程中黏性主要影响相对扰动幅度的中后期衰减,且随着黏性系数增加衰减速率减小,零点相对距离增大,最大反向幅度减小,即黏度越大衰减曲线曲率越小[14],这一研究将另文叙述。观察图4和图6,云团扩散速度会在初始驱动后短时间内达到最大,而后以指数形式衰减,增大液体黏度,会使扩散速度衰减曲线曲率随之减小。 图5 3号工况条件下云团半径随时间变化曲线 Fig.5 The comparison chart of the measured radius changing with time curve and simulation curve (Third Condition) 图6 3号工况条件下云团扩散速度随时间变化曲线 Fig.6 The comparison chart of the measured velocity changing with time curve and simulation curve (Third Condition) 由图7、8可知,1号工况得到的大液滴个数明显大于3号,此情形与试验观察到的现象一致,说明当液体黏性增大,即Ohnesorge数较大时,液滴将难以破碎或者不能破碎。 图7 1号工况条件下液滴尺寸分布图 本文进行了黏性液体爆炸抛撒机理研究并开展试验,得到结论如下: 图8 3号工况条件下液滴尺寸分布图 (1) 结合经验与理论公式,修正速度方程和液滴破碎黏度参数,耦合近场驱动动力学和远场飞散动力学,获得黏性液体爆炸抛撒全过程数学模型,其准确性得到试验验证。 (2) 黏度对云雾状态的影响随着时间的增长,抛撒半径与黏度成正比关系。 (3) 云团扩散速度会在初始驱动后短时间内达到最大,而后以指数形式衰减。增大液体黏度,会使扩散速度衰减曲线曲率随之减小。 [1] KUDRYASHOYA O B, VOROZHTSOV B I, KOROVINA N V, et al. Physicomathematical modeling of the explosive dispersion of liquid by a centrifugal atomizer[J]. Propellants, Explosives, Pyrotechnics, 2013, 38:505-510. [2] 薛社生, 刘家骢, 彭金华. 液体燃料爆炸抛撒的近场阶段研究[J].南京理工大学学报, 1997, 21(4): 333-336. XUE Shesheng, LIU Jiacong, PENG Jinhua. Study on the explosively dispersed liquid fuel in the near-field[J]. Journal of Nanjing University of Science and Technology, 1997, 21(4): 333-336. [3] 薛社生, 刘家骢, 秦承森. 燃料爆炸抛撒成雾的实验与数值研究[J]. 爆炸与冲击, 2001, 21(4):272-276. XUE Shesheng, LIU Jiacong, QIN Chengsen. Experimental and numerical investigationon explosive dispersal and cloud forming[J]. Explosion and Shock Waves, 2001, 21(4):272-276. [4] 丁珏, 刘家骢. 液体燃料爆炸抛撒和FAE 形成过程的数值模拟[J].南京理工大学学报, 2000, 24(2): 168-171. DING Jue, LIU Jiacong. Numerical simulation on the process of explosive dispersal for forming FAE cloud[J]. Journal of Nanjing University of Science and Technology, 2000, 24(2): 168-171. [5] 丁珏, 刘家骢, 彭金华. 液体燃料爆炸抛撒近场阶段的数值研究[J]. 爆炸与冲击, 2000, 20(3):215-220. DING Jue, LIU Jiacong, PENG Jinhua. Numerical study on the explosively dispersed liquid fuel in the near-field[J]. Explosion and Shock Waves, 2000, 20(3):215-220. [6] 秦承森,王裴,王丽丽,等. 液体环轴对称抛洒首次破碎的理论分析[J]. 爆炸与冲击, 2007, 27(3): 198-203. QIN Chengsen, WANG Pei, WANG Lili, et al. An investigation of the primary breakup in the axisymmetric dissemination of a liquid ring[J]. Explosion and Shock Waves, 2007, 27(3): 198-203. [7] 方伟, 赵省向, 李文祥, 等. 爆炸抛撒过程中 FAE 云雾的运动特性[J]. 含能材料, 2015, 23(11):1061-1066. FANG Wei, ZHAO Shengxiang, LI Wenxiang, et al. Movement characteristics of fuel-air explosive (FAE) clouds in the explosion dispersal process[J]. Chinese Journal of Energetic Materials, 2015, 23(11):1061-1066. [8] 罗琳, 解立峰, 韩志伟, 等. 柴油的抛撒成雾及燃爆特性研究[J]. 高压物理学报, 2015, 29(3):213-218. LUO Lin, XIE Lifeng, HAN Zhiwei, et al. Cloud character in explosion dispersion and combustion feature of diesel[J]. Chinese Journal of High Pressure Physics, 2015, 29(3):213-218. [9] 吴德义. 冲击波作用下液体抛撒和界面运动研究[D].合肥:中国科技大学, 2002. [10] GRADY D E. The spall strength of condensed matter[J]. Journal of the Mechanics & Physics of Solids, 1988, 36(3):353-384. [11] LIN S P. Breakup of liquid sheets and jets[M].The Press Syndicate of the University Of Cambridge,2003. [12] LIN S P, REITZ R D. Drop and spray formation from a liquid jet[M]. Annu. Rev. Fluid Mech., 1998, 30:85-105. [13] CORINO E R, BRODKEY R S. A visual investigation of the wall region in turbulent flow[J]. Journal of Fluid Mechanics, 1969, 37:1-30. [14] 马小娟,刘福生,李一磊,等. 冲击压缩下物质黏性系数与冲击波阵面扰动衰减特性研究[J].物理学报,2010,59(7):4761-4766 MA Xiaojuan,LIU Fusheng, LI Yilei, et al. Quantitative relation between the viscosity coefficient of substances under shock compression and the disturbance damping of shock from[J]. Acta Physica Sinica, 2010,59(7):4761-4766. ViscousliquidexplosiondispersionModel KANG Kai1,2, MA Feng2, WANG Hongying1, WANG Shushan2 (1. State Key Laboratory of NBC Protection for Civilian, Beijing 102205, China;2. State Key Laboratory of Explosion Science and Technology Beijing Institute of Technology, Beijing 100081, China) To build the model for viscous liquid explosion dispersion is of great significance to numerically simulating viscous liquid explosion dispersal process. The explosion dispersion of viscous liquid is a complex physical process including initial driving of fluid, cavitation effect, formation of fluid ring, formation and fracture of jets, droplet breakup. According to flow characteristics in different stages and different phenomena, the mathematics model of Newtonian viscous fluid’s explosion dispersion was established. The liquid dispersal velocity, the fluid dispersal radius and the distribution of droplets size were obtained through calculation. The results showed that the fluid dispersal radius is proportional to the fluid viscosity, while the curvature of the fluid dispersal velocity attenuation curve is inversely proportional to the fluid viscosity. The test was designed to verify the correctness of the mathematical model. It was shown that the test results agree well with those of calculation, the correctness of the model is verified. viscous liquid; explosion dispersion process; mathematical model; test study 2016-04-11 修改稿收到日期:2016-07-11 康 凯 男,硕士,助理工程师,1988年11月生 马 峰 男,博士,副研究员,1973年10月生 O389 : A 10.13465/j.cnki.jvs.2017.17.022

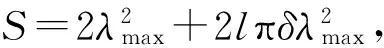
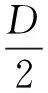
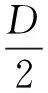
2 实验研究


3 黏性液体爆炸抛撒特征计算
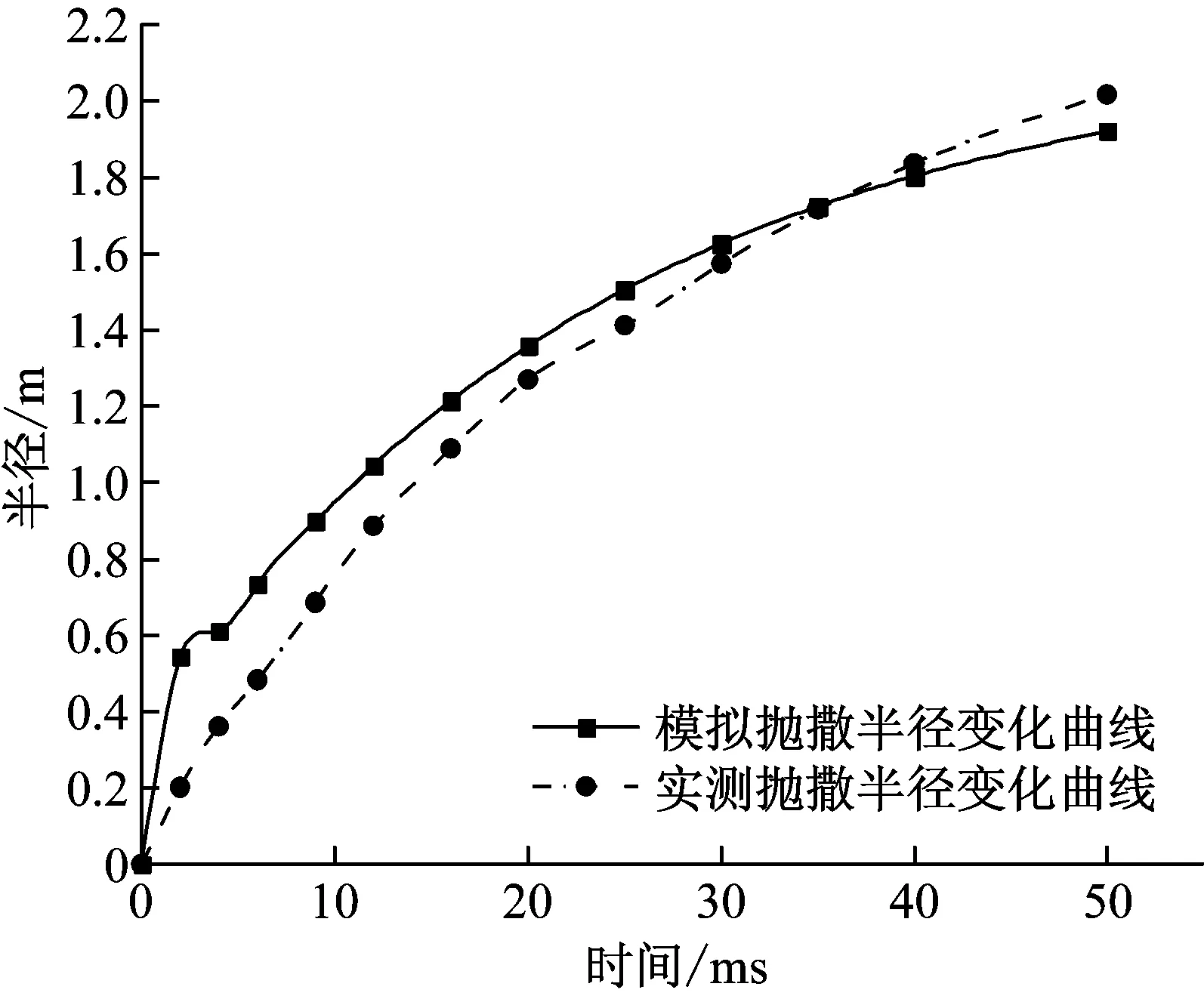
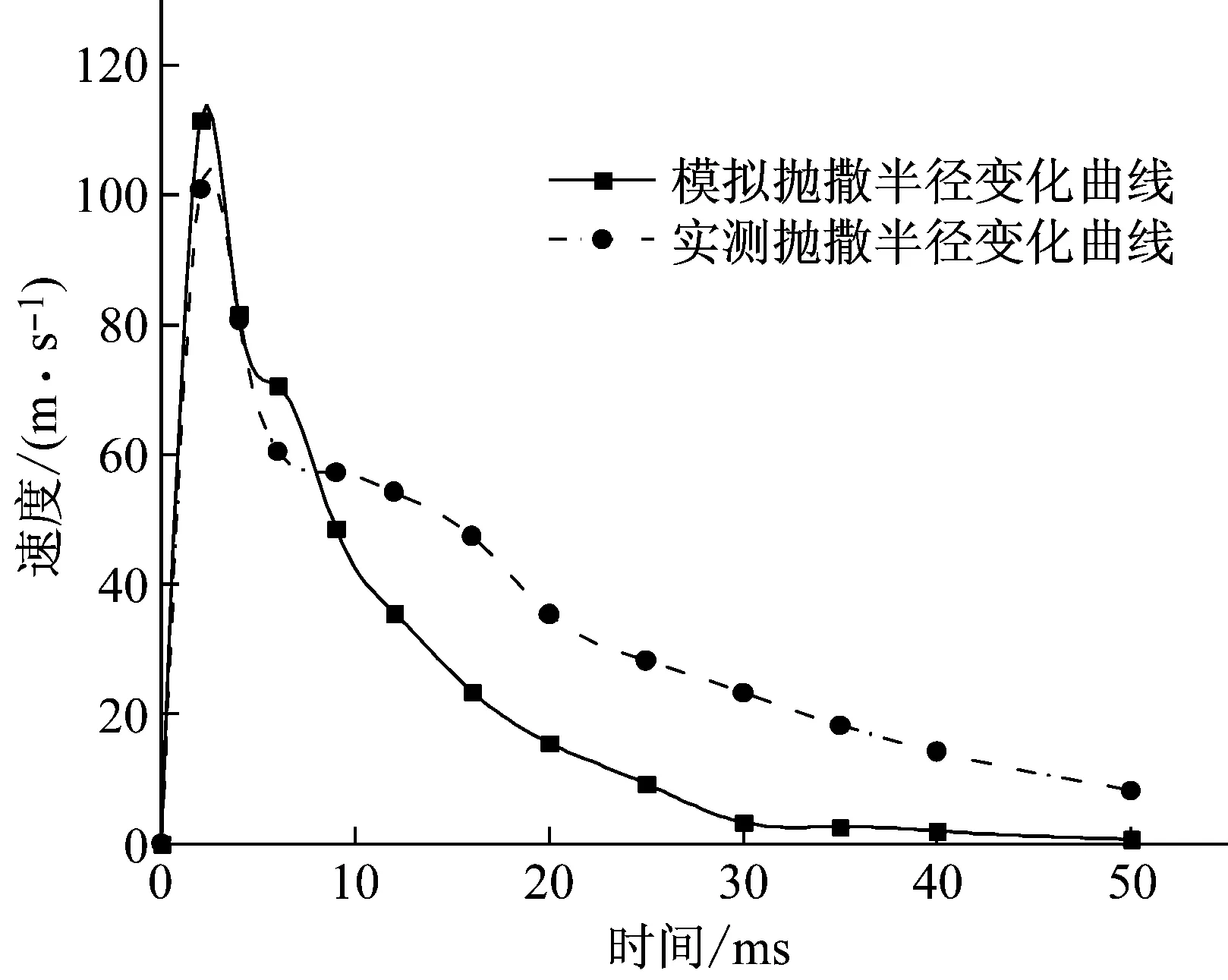
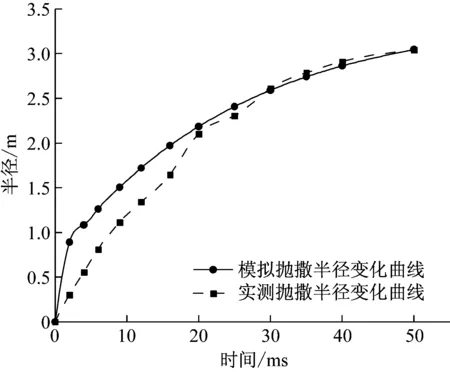
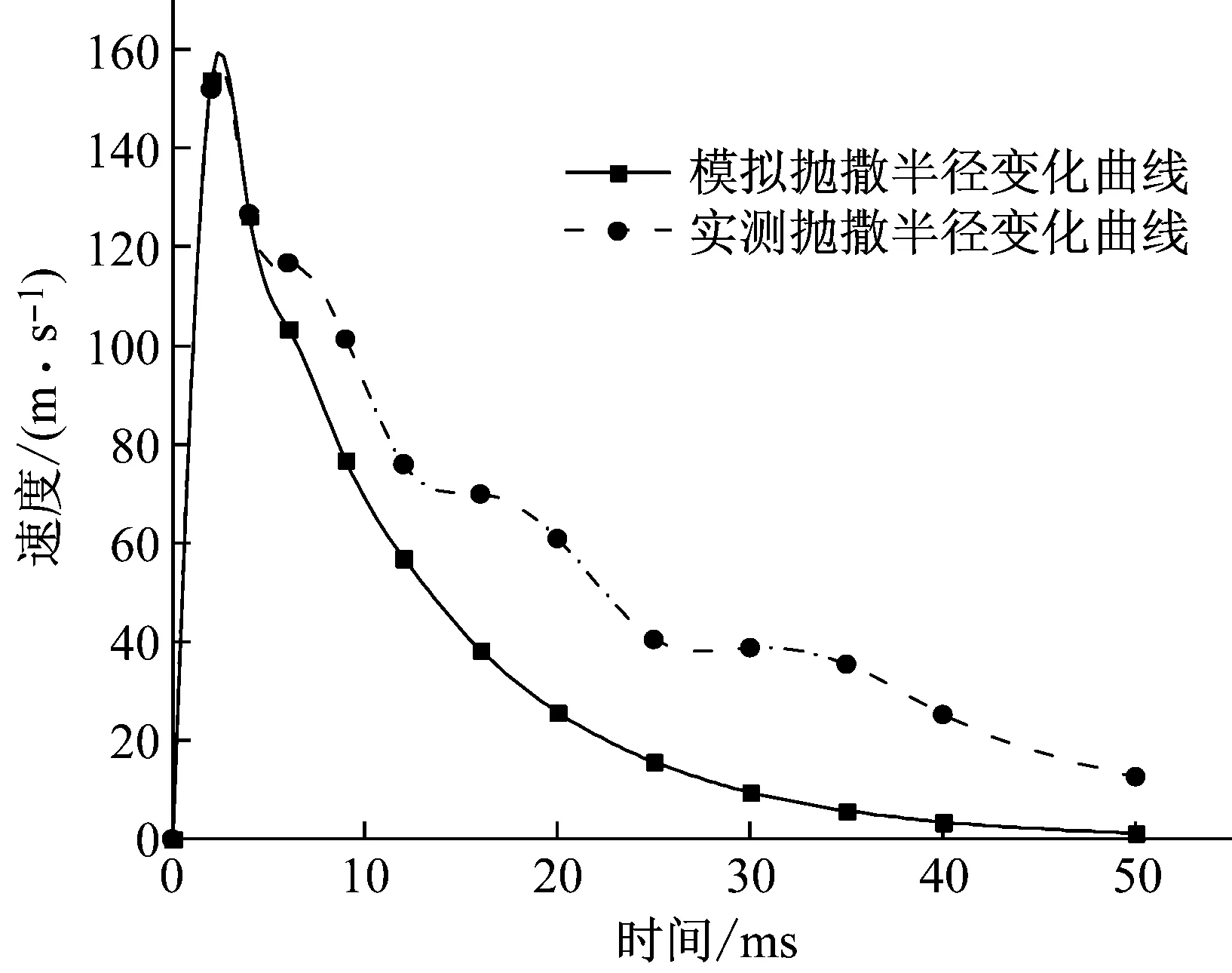
4 结 语