再入飞行器大攻角飞行时的姿态控制律设计
2017-09-12刘满国李宪强李苑青
成 高,刘满国,李宪强,张 翔,李苑青
(1.西安现代控制技术研究所,西安 710065;2. 北京空间技术研制试验中心,北京 100094)
再入飞行器大攻角飞行时的姿态控制律设计
成 高1,刘满国1,李宪强2,张 翔1,李苑青1
(1.西安现代控制技术研究所,西安 710065;2. 北京空间技术研制试验中心,北京 100094)
再入飞行器大攻角飞行时,会造成方向舵失效,且较小的滚转角速度,就可能导致舵偏指令饱和,对此,本文设计了一种在方向舵失效情况下的抗饱和姿态控制律。该控制律首先基于时标分离假设,将再入飞行器大攻角飞行时的姿态运动模型分解成快、慢回路子系统,然后采用新型的高阶滑模控制律,设计出了一种有限时间收敛且连续可导的慢回路控制器;针对快回路子系统,结合分层滑模控制理论和自适应控制理论,设计了具有抗输入饱和功能的自适应分层滑模控制器。对以上控制器进行仿真验证,结果表明该控制律在大攻角飞行造成偏航舵失效情况下,具有良好的抗饱和姿态控制能力。
再入飞行器;大攻角;滑模控制;抗饱和
0 引 言
再入飞行器大攻角飞行时,能够在高空中增加阻力,快速降低系统的速度并有效避免系统的极限热效应,从而降低对热防护系统的要求[1]。但是再入飞行器在大攻角飞行时,会造成方向舵形式的气动舵失效[2-3],例如,X-38在从71 km下降到38 km 这一大攻角飞行阶段,偏航舵失效,只用两个体襟翼来控制[2]。此外,飞行器在大攻角飞行时,飞行器通道间的气动耦合与惯性交感耦合加大,较小的滚转角速度就很容易引起执行机构的饱和。
当方向舵形式的舵偏失效后,系统只有两个输入,此时如果采用常用的基于动态逆的方法时,只能对三个状态中的两个进行输入输出线性化,很可能产生不稳定内动态或内动态稳定度下降[4],给控制系统的设计带来了挑战,目前文献中披露的绝大多数的再入飞行器的控制方法[5]将不再适用,因此必须合理地处理系统的内动态。目前,飞行控制中处理内动态的方法,主要以下几类:1)直接忽略的方法[6],这类方法仅适用内动态对系统的稳定性影响很小的系统;2)输入重定义方法[7],该方法通过重新定义系统的输入,保证对内动态的稳定控制;3)输出重定义方法[8],通过重新定义系统输出,确保零动态稳定;4)增加控制面的方法[9],通过增加额外的控制输入以抵消内动态带来的影响,此类方法需要重新设计气动,代价较高;5)动态滑模方法[10],通过设计动态滑模面,将传统滑模控制与动态补偿器的优点相结合,实现对存在内动态系统的动态稳定控制;6)稳态逆控制[11],通过转换,使存在内动态系统变成一个特定形式的系统,在此基础上设计期望的控制输入;7)系统分解法[12-13],首先采用输入输出线性化,确定系统的外动态和内动态,然后将外动态及与之线性相关的内动态组成低维子系统,然后采用高增益控制器确保系统的稳定性。以上方法都比较有效地保证了系统中内动态的稳定性,但是目前披露的文献中,大部分控制方法通常没有考虑输入饱和非线性问题,而对于实际物理系统,其输入普遍存在饱和非线性特性[14-15],输入饱和会引起动态性能下降,甚至导致系统的不稳定[16],因此研究存在内动态系统的抗饱和控制问题具有重要的理论意义。飞行器大攻角飞行时,机体的遮挡造成了偏航舵失效,形成具有内动态的系统[17-18],此外通道间的惯性耦合加大,较小的滚转角速度就很容易引起输入饱和,因此飞行器的运动学和动力学模型不但具有内动态,而且存在着输入饱和非线性特性,严重影响着飞行器的飞行安全。因此,研究再入飞行器大攻角飞行时的抗饱和控制问题对于飞行器的安全飞行具有重要的意义。
本文首次设计了可保证再入飞行器大攻角飞行时,偏航舵失效时的抗饱和控制器,以确保其在大攻角情况下的安全飞行。设计过程中,首先将系统分成快、慢回路,其次采用高阶滑模控制方法,设计了连续且可导的慢回路滑模控制器,该控制器不但能够对慢回路干扰进行有效抑制而且具有一定的抗滑模抖振功能;在快回路子系统控制器的设计过程中,采用分层滑模控制理论对系统的输出进行了重定义,并将其作为滑模面,然后结合自适应控制理论设计了一种自适应分层滑模控制器,该控制器不但可避免系统内动态的不稳定,而且具有抗输入饱和能力,因此最终保证了飞行器在偏航舵失效存在内动态情况下的抗饱和控制能力。
1 模型分析及问题描述
再入飞行器大攻角飞行时,会造成气动形式的方向舵失效,此时考虑输入饱和约束时的姿态运动学和动力学模型如下[2]:
(1)
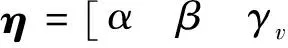
(2)
其中,i=e,α,δi_MAX为最大舵偏角,输入矩阵为
(3)
输入矩阵B以及其它各项的具体形式可见文献[2]。
基于时标分离假设[16],系统可以分解成如下快、慢回路子系统:
(4)
(5)
通过分析可知,快回路子系统(4)只有两个输入变量,因此只能对式(4)中三个状态中的两个进行输入输出线性化,此时另外一个状态将会变成内动态,如果控制器不能有效保证内动态的稳定性,会导致整个系统不稳定[2]。
2 控制器设计
本节基于大攻角飞行时的再入飞行器姿态运动模型设计控制器。基于时标分离假设,把系统分成快、慢回路子系统,然后设计相应的控制器,其具体思想如图1所示。
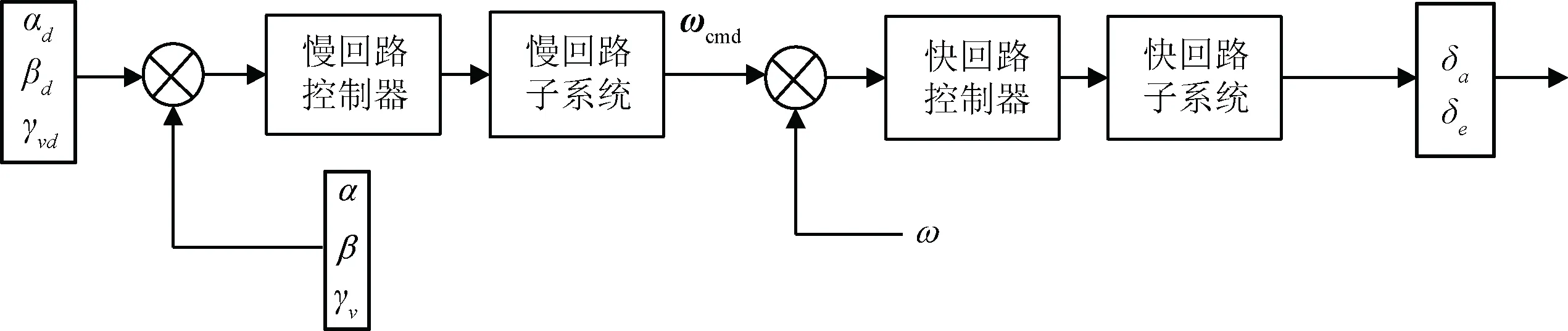
图1 时标分离假设下的控制结构图Fig.1 Control structure under time-scale assumption
2.1 慢回路子系统控制器设计
(6)
将式(1)代入上式可得
(7)
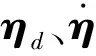
假设2. 矩阵Ξ(η)是非奇异的。
引理1(高阶超扭曲算法)[19].考虑如下系统
(8)
其中,
υ为干扰,且存在Lipschitz常数L,如果参数满足以下条件:
则状态xi(i=1,…,n)能够有限时间收敛到零点。
定理1. 对于系统式(6),设计如下虚拟控制器
(9)
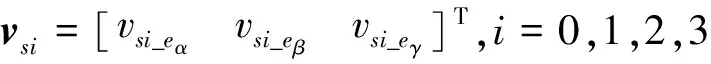
(10)
式中:k=eα,eβ,eγ。当λi>0(i=1,…,3),λ4>Ld系统(6)中的状态eη能够有限时间内收敛到零点。
证.将式(9)代入式(6)可得
(11)

(12)
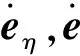
注2. 式(9)中的伪控制指令ωcmd是可导的。
2.2 快回路子系统控制器设计
选取式(9)中的ωcmd作为参考角速率指令,并选取角速率跟踪误差eω=ω-ωcmd作为状态,则根据式(4)得出快回路子系统的跟踪误差状态方程为
(13)
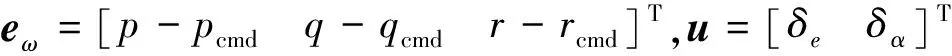
令输入为
δe=δe_eq+δe_s
(14)
δα=δα_eq+δα_s
(15)
结合式(14)和(15),则包含饱和特性的输入可表示为
sat(δe)=χ(δe)(δe_eq+δe_s)
(16)
sat(δα)=χ(δα)(δα_eq+δα_s)
(17)
(18)
其中,i=α,e且系数χ(δi)∈(0,1]可被视为δi的饱和程度。式(16)和(17)可进一步写成
(19)
(20)
结合式(13),选取
(21)
并采用如下分层滑模面[21]
stotal=z1+h1z2+h2z3
(22)
引理2[22].式(22)中,h1和h2分别取值如下
(23)
(24)
则当stotal收敛到零点时,zi(i=1,2,3)也会收敛到零点。
假设3. 存在一个非零常值σ满足0<σ≤χ(δi)≤1(i=e,α)。
假设4. 令
(25)
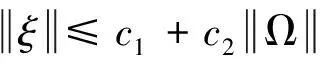
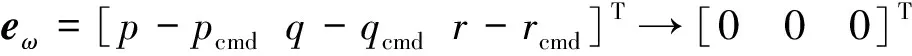
(26)
其中,
(27)
(28)
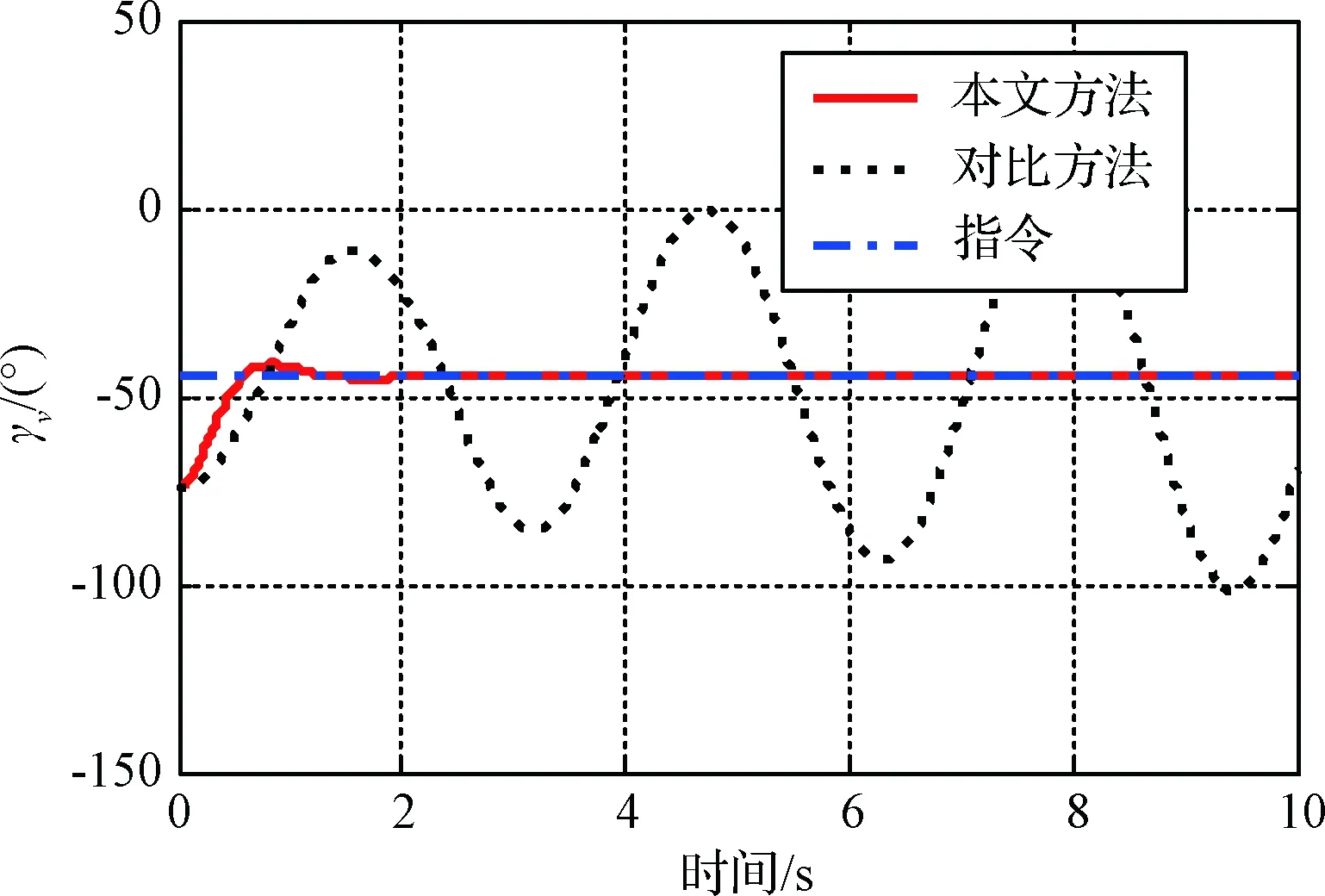
其中,ksi>0,εi>0,bi>0, 0 (29) (30) 式(30)中的参数满足如下自适应律 (31) 其中,p1和p2为待设计的正常值。 证明.对于系统(13),取李雅普诺夫函数如下: (32) 对式(22)等号两边求导,并代入式(13)、(19)和(20),可得 (33) 其中,Fs和ξ的具体表达式见式(29)和式(25)。 对式(32)进行求导,并代入式(33),可得 (34) 将式(27)代入式(34)中,可得 (35) 根据式(35)可得 (36) 根据假设4可得 (37) 结合假设3,将式(28)和(30)代入式(37),可得 (38) 根据式(38)可得 (39) 根据式(31)可得 (40) (41) 将方程(40)和(41)代入不等式(38)可得 (42) 注3. 由于式(26)表示的控制输入δi有界,因此式(18)中χ(δi)为非零值,所以假设3是合理的。 注4. 输入饱和时,控制器的输出与被控对象的输入不一致,采用自适应律对二者的差值进行估计并反馈到控制指令中,从而在发生饱和时,系统可以自动降低控制输入指令,减缓饱和的程度。 仿真过程中飞行器的气动参数以及其它参数见文献[19],在本文仿真中,考虑了气动参数的不确定性,将参数在±35%的误差范围内,随机拉偏,参数偏差随着仿真时间不断变化。 3.1 大攻角飞行舵偏不发生饱和时的仿真 根据仿真结果可知,对于本文的控制方法,在偏航舵失效,但俯仰舵和滚转舵不存在输入饱和的情况下(图2~3),本文设计的控制器能够保证对攻角和倾侧角指令的有效跟踪(见图4、图6),同时在30°的阶跃倾侧角指令和5°阶跃攻角指令下,侧滑角的幅值也能够被严格限制在3°以内(见图5)。此外经过对比可知,本文方法与文献[2]中的方法效果类似(见图2~6)。综上,本文的控制方法在不存在饱和输入情况下,能够对偏航舵失效的再入飞行器进行有效地姿态控制。 图2 没有发生饱和的控制输入δαFig.2 Control input δα with no saturation 图3 没有发生饱和的控制输入δeFig.3 Control input δe with no saturation 图4 没有发生输入饱和时的攻角α响应Fig.4 Attack-angle α responses under no input saturation 图5 没有发生输入饱和时的侧滑角β响应Fig.5 Side-slip angle β responses under no input saturation 图6 没有发生输入饱和时的倾侧角γv响应Fig.6 Bank-angle γv responses under no input saturation 3.2 大攻角飞行且舵发生饱和时的仿真 根据仿真结果可知:初始时刻,虽然两种方法都发生了饱和现象(见图7~8),但是经过较短时间后,本文方法的输入能够很快不再饱和,而且对于攻角、侧滑角和倾侧角的控制效果也较好(见图9~11);文献[2]方法的输入始终处于饱和状态,同时造成了角度输出震荡(见图9~11)。 图7 发生饱和的控制输入δαFig.7 Control input δα with saturation 图8 发生饱和的控制输入δeFig.8 Control input δe with saturation 图9 发生输入饱和时的攻角α响应Fig.9 Attack-angle α responses under input saturation 图10 发生输入饱和时的侧滑角β响应Fig.10 Side-slip angle β responses under input saturation 图11 发生输入饱和时的倾侧角γv响应Fig.11 Bank-angle γv responses under input saturation 在输入饱和情况下,本文方法具有良好控制效果的原因,是由于文中设计的控制器含有自适应控制律,该控制律能够在输入饱和时(控制器的输出与被控对象的输入不一致),对控制器的输出与被控对象的输入之间的差值进行估计并反馈到控制指令中,从而在发生饱和时,系统可以自动降低控制输入指令,减缓饱和的程度,避免输出发生震荡现象,以保证控制性能。 本文针对大攻角飞行造成偏航舵失效情况下的再入飞行器,设计了具有抗饱和功能的姿态控制器,通过仿真结果表明,该控制器不但能够有效保证系统的稳定性,而且能够在飞行器剩余的俯仰舵和滚转舵发生饱和时,依然具有良好的控制性能。 [1] Atkinson M, Poggie J, Camberos J. Control of high-angle-of-attack reentry flow with plasma actuators [J]. Journal of Spacecraft and Rockets, 2013, 50(2): 337-346. [2] Wallner E M, Well K H. Attitude control of a reentry vehicle with internal dynamics [J]. Journal of Guidance, Control, and Dynamics, 2003, 26(6): 846-854. [3] Yayla S, Canpolat C, Sahin B, et al. The effect of angle of attack on the flow structure over the nonslender lambda wing [J]. Aerospace Science and Technology, 2013, 28(1): 417-430. [4] Cannon M, Bacic M, Kouvaritakis B. Dynamicnon-minimum phase compensation for SISO nonlinear, affine in the input systems[J]. Automatica, 2006, 42(11): 1969-1975. [5] Kawaguchi J, Ninomiya T, Miyazawa Y. Stochasticapproach to robust flight control design using hierarchy-structured dynamic inversion [J]. Journal of Guidance, Control, and Dynamics, 2011, 34(5): 1573-1576. [6] 罗建军, 常江, 王章磊, 等. 滑翔式高超声速飞行器大包线状态反馈控制 [J]. 宇航学报, 2014, 35(2): 192-199.[Luo Jian-jun, Chang Jiang, Wang Zhang-lei, et al. State Feedback control for gliding hypersonic vehicle in wide flight envelope [J]. Journal of Astronautics, 2014, 35(2): 192-199.] [7] Sun H, Yang Z, Zeng J. New tracking-control strategy for airbreathing hypersonic vehicles [J]. Journal of Guidance, Control, and Dynamics, 2013, 36(3): 846-859. [8] 路遥,王青,董朝阳. 输出重定义的高超声速飞行器鲁棒自适应控制律设计[J].宇航学报,2014, 35(3): 331-339.[Lu Yao,Wang Qing, Dong Chao-yang. A Study on output redefinition robust adaptive control method for hypersonic vehicle [J]. Journal of Astronautics ,2014, 35(3): 331-339.] [9] Fiorentini L, Serrani A, Bolender M A, et al. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles [J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 402-417. [10] Sira-Ramirez H. A dynamical variable structure control strategy in asymptotic output tracking problems [J]. IEEE Transactions on Automatic Control, 1993, 38(4): 615-620 [11] Devasia S, Chen D G, Paden B. Nonlinear inversion-based output tracking [J]. IEEE Transactions on Automatic Control, 1996, 41(7): 930-942. [12] Su S W, Lin Y. Robust output tracking control of a class of non-minimum phase systems and application to VTOL aircraft [J]. International Journal of Control, 2011, 84(11): 1858-1872. [13] Al-Hiddabi S A, Mc Clamroch N H. Tracking and maneuver regulation control for nonlinear non-minimum phase systems: application to flight control [J]. IEEE Transactions on Control Systems Technology, 2002, 10(6): 780-792. [14] Corradini M L, Cristofaro A, Orlando G. Robust stabilization of multi input plants with saturating actuators [J]. IEEE Transactions on Automatic Control, 2010, 55(2): 419-425. [15] Grip H F, Saberi A, Wang X. Stabilization of multiple-input multiple-output linear systems with saturated outputs [J]. IEEE Transactions on Automatic Control, 2010, 55(9): 2160-2164. [16] Menon P P, Lowenberg M, Herrmann G, et al. Experimental implementation of a nonlinear dynamic inversion controller with anti-windup [J]. Journal of Guidance, Control, and Dynamics, 2013, 36(4): 1035-1046. [17] Adams R J, Buffington J M, Banda S S. Design of nonlinear control laws for high-angle-of-attack flight [J]. Journal of Guidance, Control, and Dynamics, 1994, 17(4): 737-746. [18] Bugajski D J, Enns D F. Nonlinear control law with application to high angle-of-attack flight [J]. Journal of Guidance, Control, and Dynamics, 1992, 15(3): 761-767. [19] Basin M V, Rodrìguez Ramìrez P C. A super-twisting algorithm for systems of dimension more than one [J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 6472-6480. [20] Levant A, Livne M. Exact differentiation of signals with unbounded higher derivatives [J]. IEEE Transactions on Automatic Control, 2012, 57(4): 1076. [21] Wang L X. Analysis and design of hierarchical fuzzysystems [J]. IEEE Transactions on Fuzzy Systems, 1999, 7(5): 617-624. [22] 王冬霞, 贾英宏, 金磊, 等. 欠驱动航天器姿态稳定的分层滑模控制器设计[J]. 宇航学报, 2013, 34(1): 17-24. [Wang Dong-xia, Jia Hong-ying, Jin Lei, et al. Hierarchical sliding-mode control for attitude stabilization of an underactuated spacecraft[J]. Journal of Astronautics, 2013, 34(1): 17-24.] 通信地址:西安市雁塔区丈八东路十号西安现代控制技术研究所(710065) 电话:(029)88293150 E-mail:572720730@qq.com 李宪强(1986-),男,工程师,主要从事先进飞行器的导航、制导与控制。本文通信作者。 通信地址:北京市海淀区友谊路104号北京空间技术研制试验中心(100094) 电话:(010)68111606 E-mail:1740679934@qq.com The Attitude Controller Design for the Reentry VehicleFlying with High Angle of Attack CHENG Gao1, LIU Man-guo1,LI Xian-qiang2,ZHANG Xiang1, LI Yuan-qing1 (1.Xi’an Modern Control Technology Research Institute, Xi’an 710065, China;2.Beijing Manufacture and Experiments Center of Space Technology, Beijing 100094, China) When a reentry vehicle flying with high angle of attack, there is always a failure of the yaw rudder. And the pitch rudder and the roll rudder are also easy to be saturated, even with a small roll angular speed. To solve this problem, an anti-windup attitude controller is presented under the failure of the yaw rudder. In the design process, based on the time-scale separation, the attitude model is separated into a fast-loop subsystem and a slow-loop subsystem firstly. Secondly, a sliding mode controller, which is differentiable and with finite-time convergence, is designed for the slow-loop subsystem through using a novel high-order sliding mode control theory. For the fast-loop subsystem, an adaptive hierarchical sliding mode controller with anti-windup capacity is designed through employing the sliding mode control theory and adaptive control theory. Finally, the presented controller is verified through simulation, and the results show that the controller has a good anti-windup capability under the failure of the yaw rudder caused by high angle of attack. Reentry vehicle; High angle of attack; Sliding mode control; Anti-windup 2016-05-30; 2017-06-13 TJ765.2 A 1000-1328(2017)08-0847-08 10.3873/j.issn.1000-1328.2017.08.009 成 高(1989-),男,助理工程师,主要从事导弹的制导、控制与半实物仿真。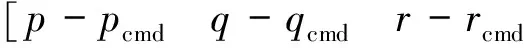
3 仿真校验
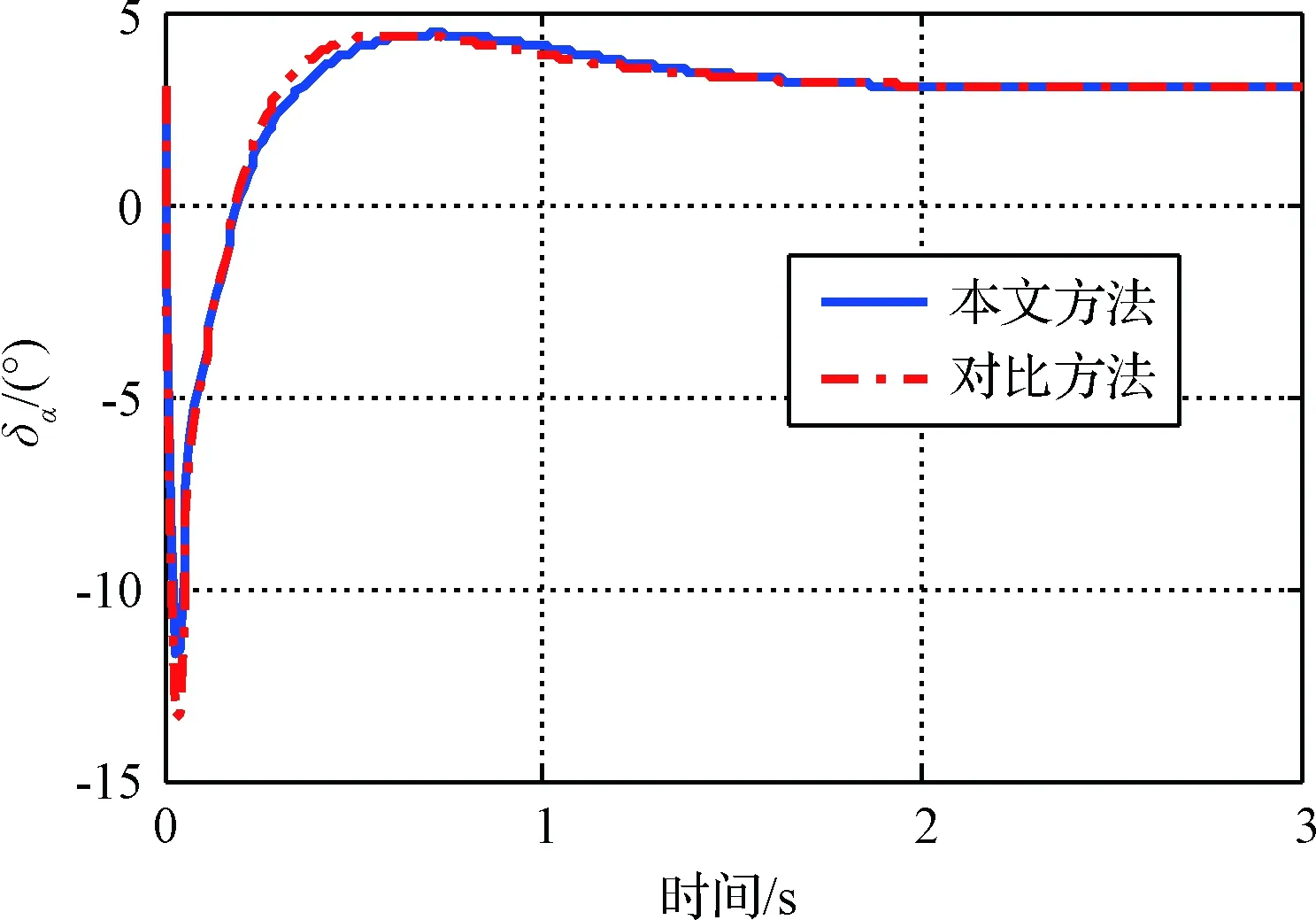

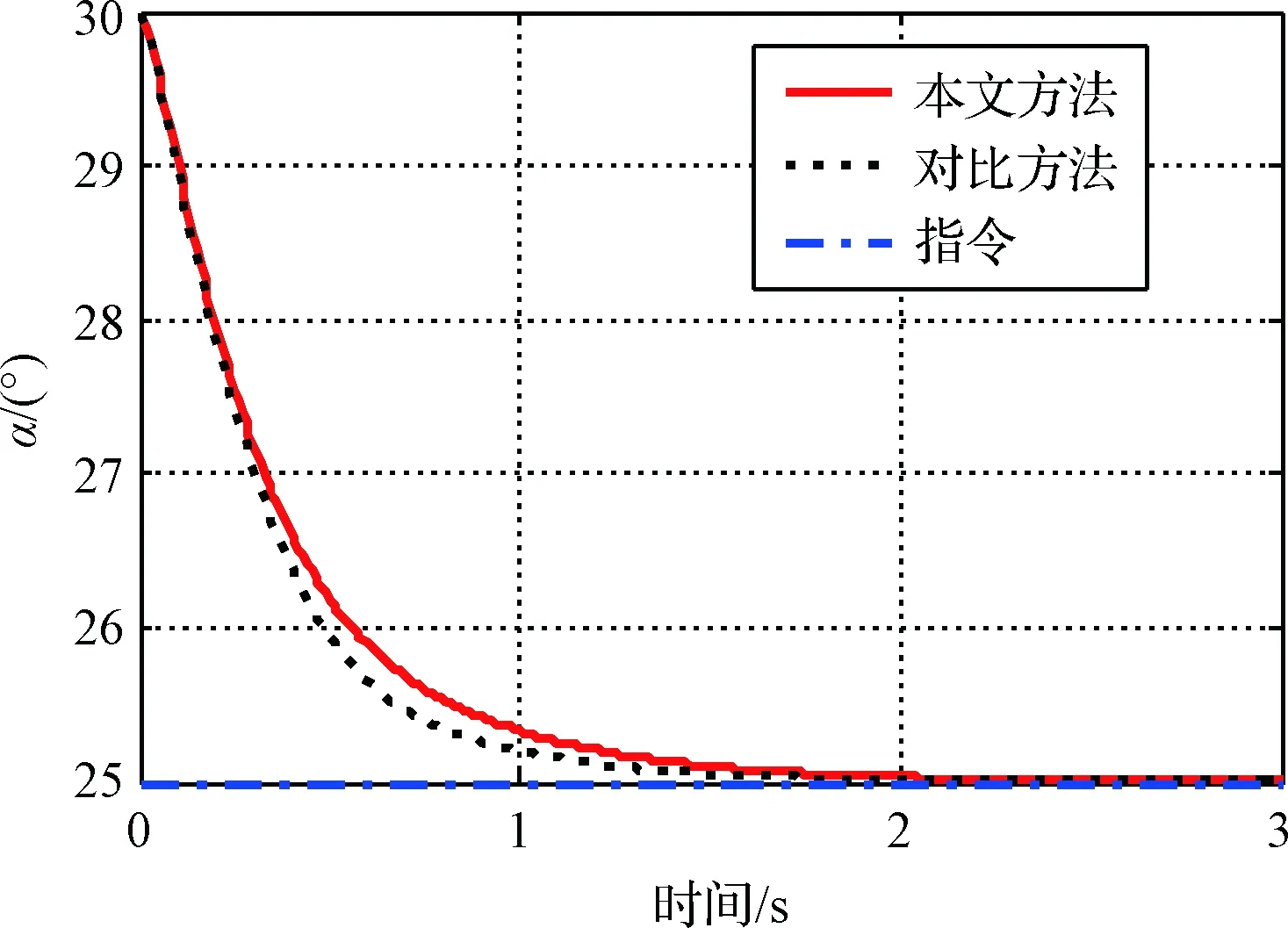
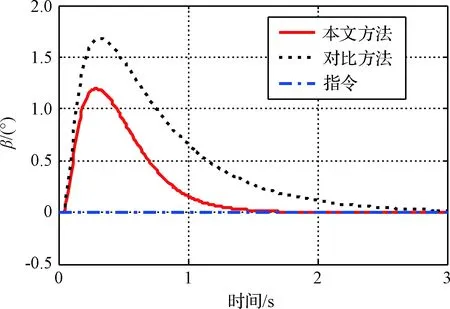
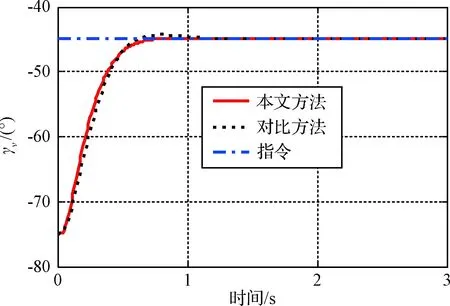
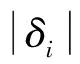


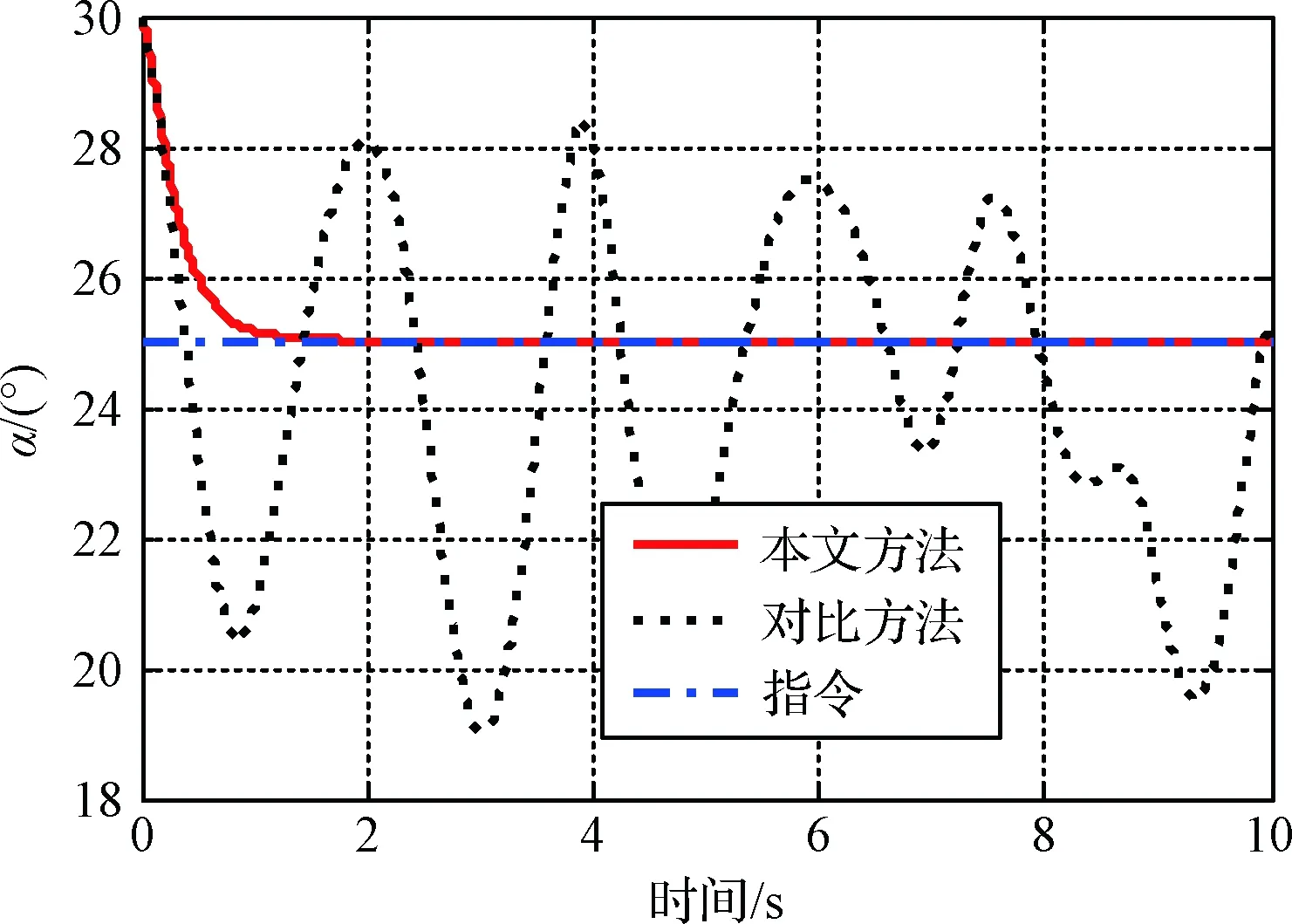

4 结 论
