高超声速飞行器多约束鲁棒姿态控制器设计
2017-09-12冯振欣郭建国
冯振欣,郭建国,周 军
(西北工业大学精确制导与控制研究所,西安 710072)
高超声速飞行器多约束鲁棒姿态控制器设计
冯振欣,郭建国,周 军
(西北工业大学精确制导与控制研究所,西安 710072)
针对高超声速飞行器机动飞行过程中存在的攻角约束和执行机构饱和非线性问题, 提出一种兼顾多约束和控制性能的鲁棒姿态控制方法。首先, 采用基于动态面法的积分型障碍Lyapunov函数(IBLF)保证攻角始终处于约束区间, 同时避免了传统反演法的“微分膨胀”问题;然后, 设计辅助误差子系统并引入控制律, 降低了高超声速飞行器输入饱和非线性对闭环系统的影响, 提高了系统的控制性能。此外, 本文还引入非线性干扰观测器对参数摄动及外部干扰进行估计和补偿, 增强了控制律的适应性。最后, 通过Lyapunov理论证明了该方法能够确保控制系统的闭环稳定性, 且闭环系统所有信号均一致有界。数值仿真结果校验了本文控制器设计的有效性。
高超声速飞行器; 攻角约束;输入饱和;障碍函数;干扰观测器
0 引 言
吸气式高超声速飞行器具备飞行速度快、远程精确打击等显著优势, 具有非常重要的经济与军事应用价值[1]。目前多个国家已经陆续开展了相关的地面和飞行试验, 吸气式高超声速飞行器技术已经成为军事领域的一个研究热点。
然而, 吸气式高超声速飞行器的控制依然存在一些难题。一方面, 由于高超声速飞行器采用机身/推进一体化设计, 导致其动力学模型具有强非线性、强耦合、强不确定性, 这无疑增加了控制难度;另一方面, 复杂的飞行环境和超燃冲压发动机严苛的工作条件(发动机性能很大程度取决于马赫数、飞行高度和姿态角)使得超燃冲压发动机的飞行走廊变得非常狭窄, 需要将飞行状态严格控制在某一确定范围内[2]。如文献[3]指出:发动机进气道的进气流量与攻角大小密切相关, 攻角过大会导致进气道进气流量急剧下降、甚至发动机不启动和热阻现象等严重后果。此外, 高超声速飞行器的燃料当量比和舵机系统均存在幅值、带宽等硬性约束, 这些约束会严重降低系统的控制性能。因此, 如何在满足诸多约束条件下确保吸气式高超声速飞行器良好的控制性能成为当下亟需解决的一个难题。
近些年, 针对吸气式高超声速飞行器约束控制问题提出了诸多方法, 如文献[4]提出基于反馈线性化的抗饱和鲁棒控制算法来解决高超声速飞行器的输入受限和不确定问题, 文献[5]则针对高超声速飞行器舵机构的死区问题进行了研究, 提出了基于Nussbaum函数的神经网络控制算法。文献[6-7]引入自适应辅助变量, 实现对控制受限下的高超声速飞行器跟踪误差和控制律的补偿。但是, 上述方法并未充分考虑高超声速飞行器的状态约束问题。
针对高超声速飞行器的状态约束问题, 文献[8]提出基于模型预测控制的高超声速飞行器控制方法, 该方法能够同时解决控制和状态约束, 但是计算量较大; 文献[2]提出LQ过载控制器+CG指令调节器相结合的方法设计控制器,能够同时满足飞行状态和舵偏约束,但是该方法对高超声速飞行器的模型精度要求较高;指令滤波器[9]近几年成为一个研究热点, 并且已经应用于高超声速飞行器的控制中[10-11]。该方法引入了控制系统对状态和控制量幅值、带宽和速率的限制, 满足了系统的控制需求。但是该方法响应速度较慢。文献[12]提出了一种解析的、能够兼顾约束和响应特性的积分障碍Lyapunov 函数, 其原理是以状态约束区间作为定义域构造Lyapunov函数, 当约束量趋向于约束条件时, 该Lyapunov函数将趋于无穷大, 设计控制器使该Lyapunov函数的导数小于零, 进而保证约束量始终处于约束区间之内。然而, 当约束状态接近或到达约束边界时, 控制量将急剧增大, 进而导致执行机构快速饱和, 因此无法单独应用于高超声速飞行器的状态约束控制中。
综合以上分析, 本文针对攻角约束和执行器饱和非线性问题提出一种解析的、同时兼顾多种约束和动态特性的高超声速飞行器鲁棒控制方法。一方面, 采用积分型障碍Lyapunov函数方法解决攻角约束问题, 确保攻角快速响应且始终处于约束区间之内。另一方面, 为保证控制器良好的控制性能,设计误差辅助子系统, 降低飞行器执行机构的饱和与动态环节对闭环控制系统的影响。同时, 考虑到参数摄动以及外部干扰对控制性能的影响, 本文引入非线性干扰观测器[13]对摄动及干扰进行估计和补偿。通过Lyapunov稳定性理论证明了控制系统的闭环稳定性, 且闭环系统所有信号均一致最终有界。
1 高超声速飞行器纵向运动模型
1.1 问题提出
高超声速飞行器纵向平面内的动力学模型[14]可描述为
(1)
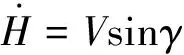
(2)
(3)
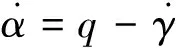
(4)
(5)
式中:V,H,γ,α,q分别为高超声速飞行器的速度、飞行高度、航迹角、攻角和俯仰角速率。Iyy,m,g分别为飞行器俯仰转动惯量、质量和重力加速度。T,D,L,Myy分别为飞行推力、阻力、升力、俯仰力矩, 可表示为[14]
(6)
鉴于实际物理结构的限制,必须考虑高超声速飞行器燃料当量比Φ和升降舵偏角δe幅值、带宽等限制对控制系统的影响。燃料当量比Φ和升降舵偏角δe满足:Φ∈[Φmin,Φmax],δe∈[δmin,δmax]。
本文借鉴指令滤波器的思想, 引入控制系统对状态和实际控制器幅值、带宽等限制(见图1), 并建立相应的补偿机制, 确保系统稳定性及动态性能。
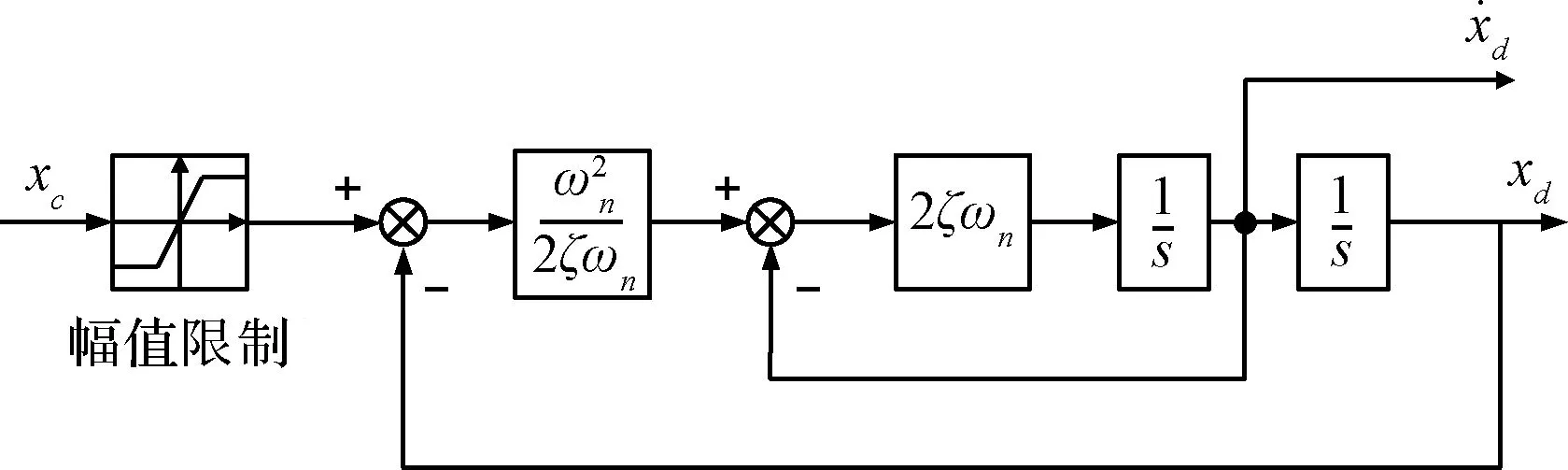
图1 带有幅值和带宽限制的指令滤波器Fig.1 Command filter with magnitude and bandwidth limit
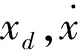
(7)
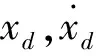
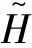
(8)
式中:kh1,kh2为待设计参数,t1为仿真时间。
因此, 高超声速飞行器纵向控制模型可分解为速度子系统和姿态子系统。
将式(6)推力T表达式代入式(1), 则有
(9)
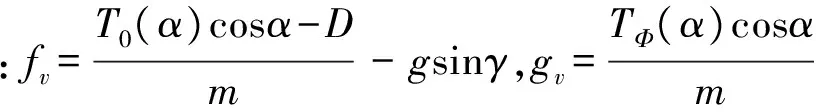
假设1. 鉴于高超声速飞行器巡航段攻角变化较小,因此近似认为sinα≈α。
令x1=γ,x2=α,x3=q, 式(3)~(5)可转换为严格反馈系统
(10)
式中:f1=L/(mV)-gcosx1/V,g1=T/(mV),f2=-(L+Tx2)/(mV)+gcosx1/V,g3=Mδe/Iyy,u=δe,f3=(MT+M0(α))/Iyy。di(i=1,2,3)包含系统非线性高阶截断误差, 参数摄动及外部干扰。
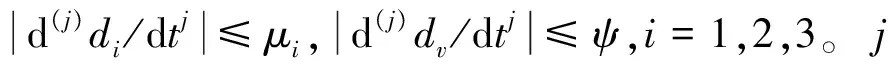
1.2 干扰观测器设计
设计非线性干扰观测器[13]如下
(11)
式中:j=1,2,χi=xi,Fi=fi,i=1,2,3,G1=g1x2,G2=x3,G3=g3u,lij>0。
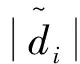
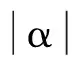
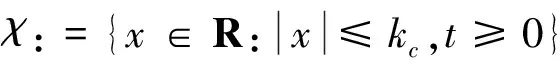
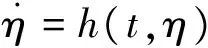
(12)
式中:η:=[ω,x]T⊂Ν, 函数h:R+×N→Rl+1关于t分段连续且关于x满足局部一致Lipschitz条件, 假设存在函数U:=Rl→R+及V:χ→R+在各自定义域正定且连续可导, 并使得
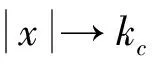
(13)
(14)
式中:γ1,γ2均为K∞类函数, 令W(η):=V+U(ω)且x(0)∈χ, 如果不等式满足
(15)
式中:μ,β>0, 则x∈χ且ω有界。证明略。
2 控制器设计
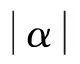
2.1 速度子系统设计
(16)
为降低燃料当量比的饱和对控制系统的影响, 设计辅助误差系统, 确保系统良好的控制性能。
(17)
(18)
设计速度子系统控制器
(19)
式中:kv,kv1>0为待设计控制器增益。
2.2 姿态子系统设计
基于动态面法, 姿态子系统设计步骤如下:
1) 令z1=x1-x1d, 对z1求导可得
(20)
选取虚拟控制量x2c
(21)
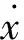
定义z2=x2-x2d,y2=x2d-x2c, 将式(21)代入式(20)有
(22)
2) 对z2求导可得
(23)
为实现攻角约束, 本文引入障碍Lyapunov函数方法, 设计虚拟控制量x3c
(24)
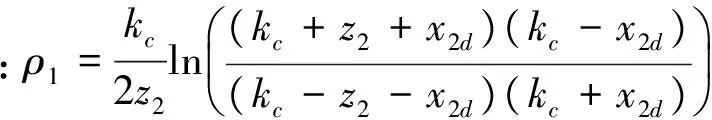
为避免虚拟控制量出现“微分膨胀”, 通过引入一阶滤波器获取新的变量x3d
(25)
式中:τ3∈(0,1)为待设计常数。
定义z3=x3-x3d,y3=x3d-x3c, 则有
(26)
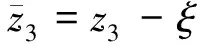
(27)
式中:ξ为误差辅助变量;ud为系统实际输出控制量,uc为控制器产生的控制指令;ξ是用来确保即使出现控制器饱和及带宽限制控制系统依然稳定。
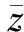
(28)
将式(27)代入式(28)可得
(29)
(30)
选取控制量为
(31)
将式(31)代入式(30)可得
(32)
2.3 稳定性分析
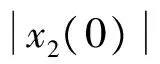
证. 选取Lyapunov函数
(33)
对W求导, 并将式(19)、 (22)、 (26)、 (32)代入,得
(34)
由y2,y3的定义可知,y2,y3满足
(35)
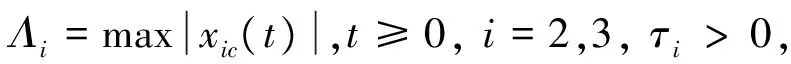
(36)
(37)
(38)
(39)
(40)
(41)
将式(35)~(41)代入式(34), 且由引理2可知,
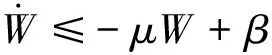
(42)
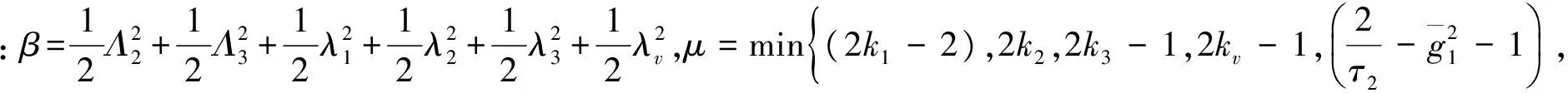
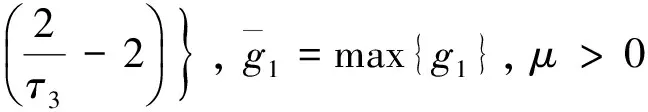
1) 对式 (42) 两边同时进行积分可得
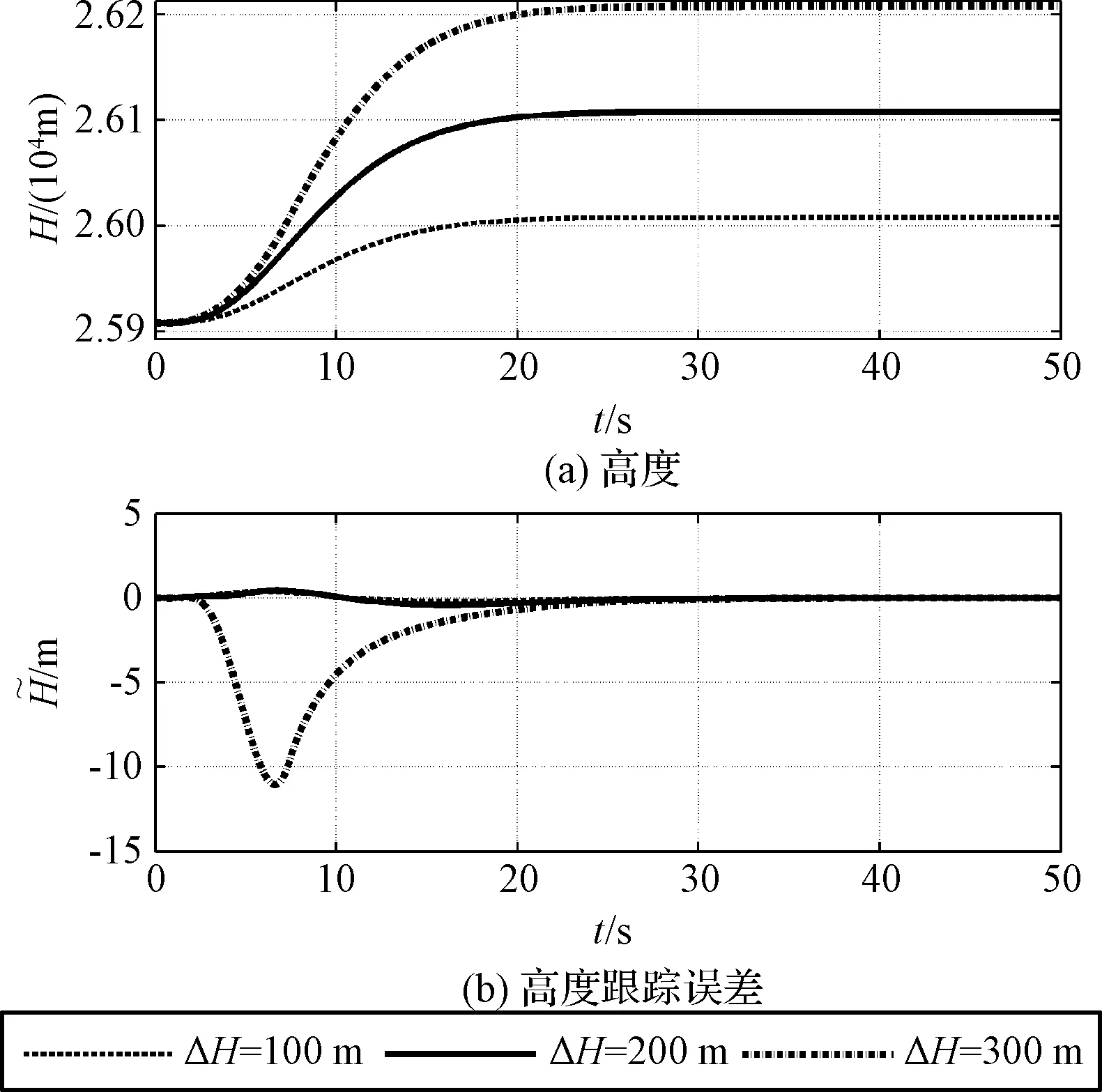
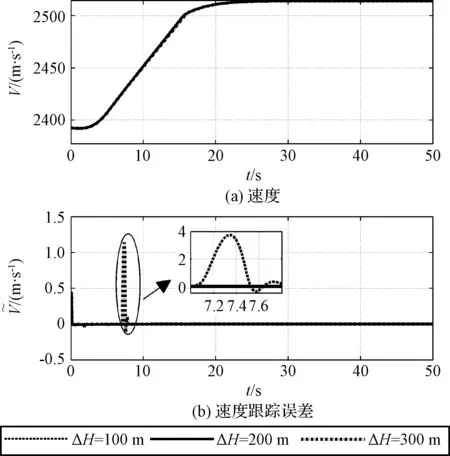
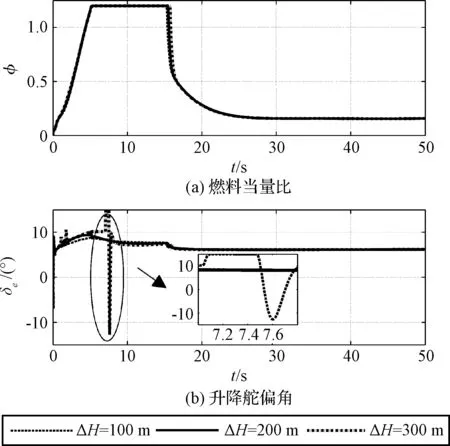
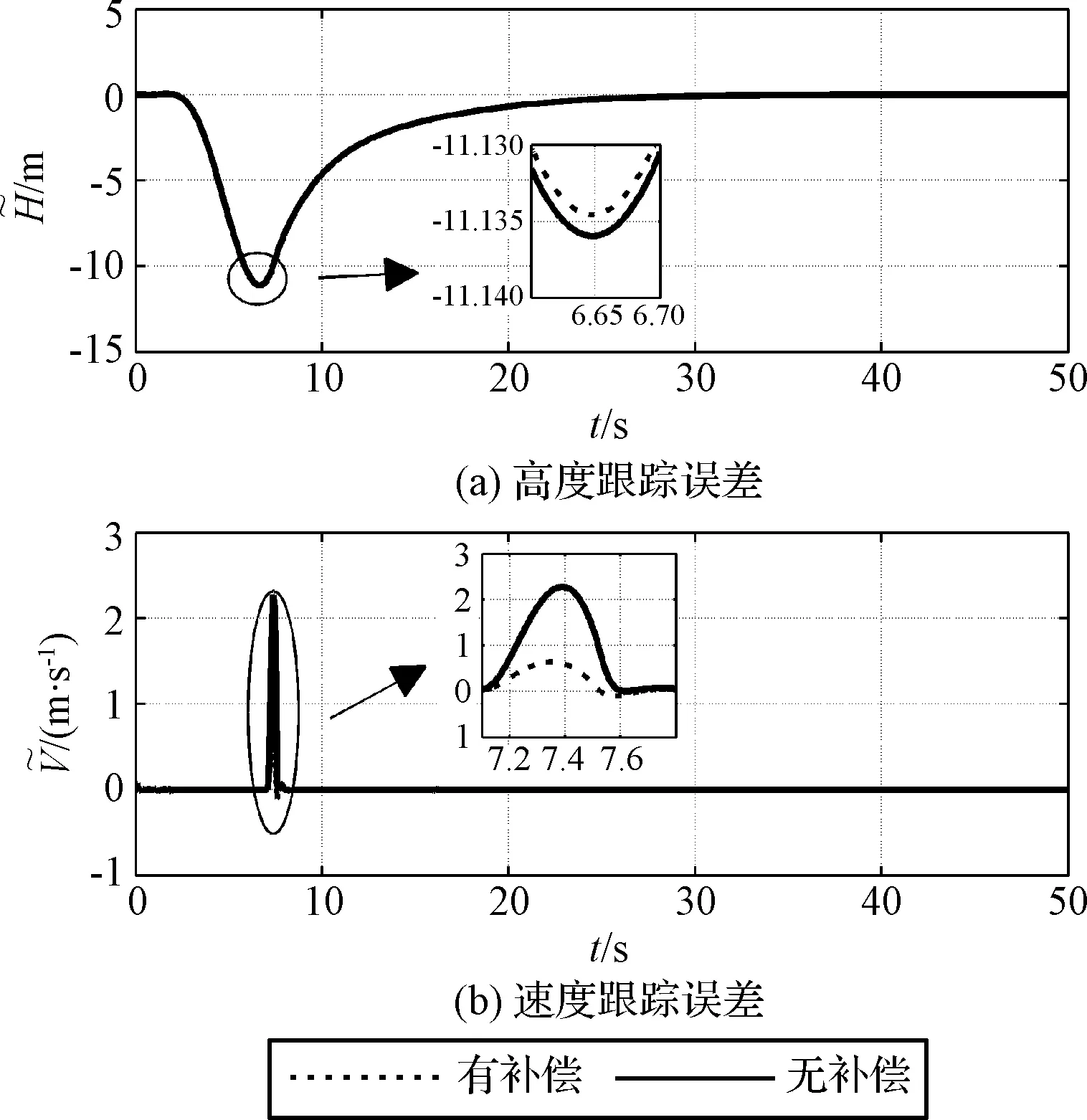
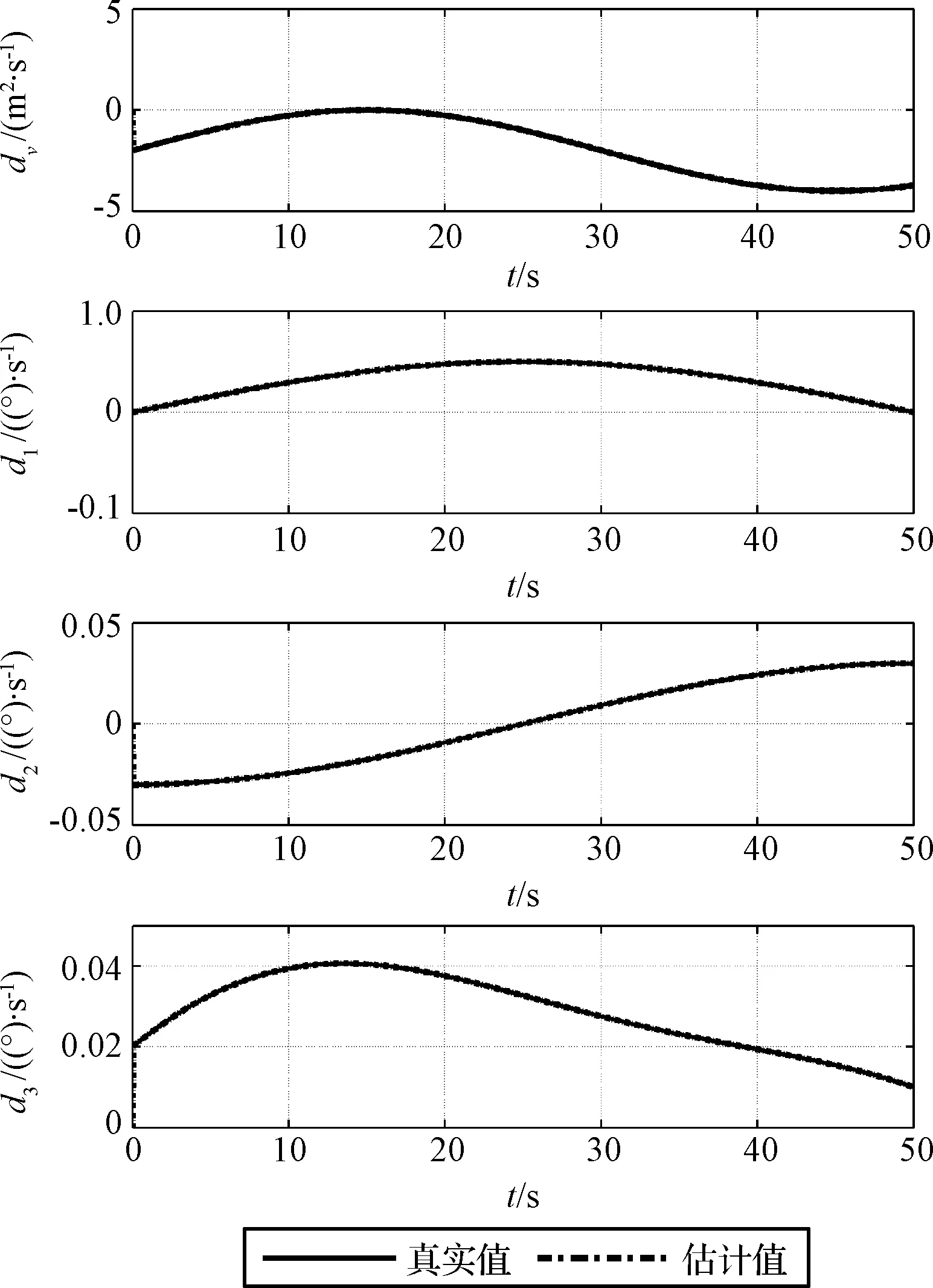
0 (43) 式中:ρ=β/μ。 注3. 执行机构的饱和及动态特性会影响闭环系统的控制性能, 甚至稳定性。因此系统控制器设计(式(17), (27))中引入了辅助补偿变量(ξv,ξ), 用以估计和补偿执行机构饱和以及动态特性所带来的影响, 由定理1知该机制能够确保闭环系统稳定性。 基于式(1)~(5)的高超声速飞行器纵向姿态模型校验本文设计控制器的控制效果, 模型及气动参数详见文献[14]。飞行器初始飞行高度为25908 m; 初始速度2310.384 m/s;γ0=0°,α0=3.5°,q(0)=0 rad/s,δe=0°。攻角和实际控制量幅值限制为:α∈[-5°,5°],Φ∈[0.05,1.2],δe∈[-15°,15°]。执行机构自然频率和阻尼分别为ωn=100,ζ=1。外部干扰形式为d1=0.05sin(ωt),d2=0.05sin(ωt)-0.03cos(ωt)-d1,d3=0.05sin(ωt)+0.02cos(ω1t),dv=2sin(ωt)-2,ω=π/50,ω1=π/30。基于Matlab/Simulink软件进行数字仿真, 要求速度子系统跟踪速度阶跃指令Vc=121.92 m/s;姿态子系统分别跟踪高度指令hc=100 m, 200 m, 300 m, 高度和速度指令分别通过滤波器F(s)[10]产生参考跟踪信号Hd和Vd。 (44) 选取控制增益kv=6,kv1=3,k1=4,k2=10,k3=20,k3=10,kh1=0.3,kh2=0.015, 一阶滤波器参数τi=0.02(i=2,3),kc=5°,干扰观测器增益li1=100,li2=20,i=1,2,3。 图2 高度及其误差跟踪曲线Fig.2 Curves of height and it’s tracking errors 图3 速度及其误差跟踪曲线Fig.3 Curves of speed and it’s tracking errors 图4 航迹角、攻角和俯仰角速率响应曲线Fig.4 Curves of flight path angle,angle of attack and pitch rate 图5 控制输入曲线Fig.5 Curves of control input 从图2可以看出, 采用本文所设计的控制器能够实现高超声速飞行器平稳跟踪参考高度指令, 且跟踪误差最终渐近收敛到零附近。图3为速度跟踪及其误差变化曲线, 可以看出姿态角及高度指令变化对速度子系统影响不大, 速度子系统能够实现快速平稳跟踪速度指令, 且跟踪误差较小。 图4为航迹角、攻角和俯仰角速率响应曲线, 可以看出随着高度指令的增大, 控制系统对攻角的需求增大, 这与高超飞行器机身/推进一体化的设计相符。当阶跃高度指令变为300 m时, 图4(b)中对应的攻角快速趋于约束边界。采用本文控制器将攻角严格限制在5°以内, 且其它飞行状态均在较小范围变化, 确保高超声速飞行器的安全平稳飞行。图5为控制输入曲线, 可以看出燃料当量比和升降舵偏角均在限制区间变化。图5(b)中, 当高度指令达到300 m时, 升降舵偏角曲线出现短暂饱和现象, 这是由于攻角快速逼近约束边界, 本文采用障碍Lyapunov函数方法对控制量需求增大所致。 为确保控制系统性能, 本文设计辅助误差变量ξv,ξ对执行机构饱和及其动态特性进行补偿, 图6分别为引入补偿和不引入补偿两种情况下高度和速度跟踪误差对比曲线, 显然引入补偿能够获取更小的跟踪误差, 提升了控制系统的控制性能。 图7为采用非线性干扰观测器对飞行器速度和姿态子系统的干扰和不确定估计曲线, 可以看出干扰估计曲线渐近跟踪实际扰动, 且估计误差较小, 因此该干扰估计器能够实现对飞行器不确定扰动的准确估计,从而降低不确定扰动对控制系统的影响。 图6 有补偿/无补偿高度和速度误差曲线Fig.6 Curves of tracking errors of height and velocity with/without compensation 图7 干扰估计曲线Fig.7 Curves of disturbance estimation 本文针对高超声速飞行器攻角约束和执行机构存在的饱和非线性问题, 提出了一种兼顾多约束和控制性能的鲁棒姿态控制方法。结合动态面法, 采用积分障碍Lyapunov函数方法解决了攻角约束问题和微分膨胀问题。然后设计辅助误差子系统补偿飞行器舵机伺服系统的动态及饱和特性对闭环控制系统的影响, 并引入干扰观测器抑制和补偿参数摄动及外部扰动的影响。最后通过Lyapunov稳定性理论证明了控制系统的闭环稳定性, 且闭环系统所有信号均有界。仿真结果表明本文方法具有较好的动态性能和抑制干扰的能力。 [1] 王建华, 刘鲁华, 汤国建. 高超声速飞行器俯冲段制导与姿控系统设计[J]. 宇航学报, 2016, 37(8): 964-973. [ Wang Jian-hua, Liu Lu-hua, Tang Guo-jian. Guidance and attitude control system design for hypersonic vehicle in dive phase [J]. Journal of Astronautics, 2016, 37(8): 964-973.] [2] 杜昊昱, 凡永华, 闫杰. 高超声速飞行器机动飞行受限控制方法研究 [J]. 西北工业大学学报, 2016, 34(6): 945-950. [Du Hao-yu, Fan Yong-hua, Yan Jie. A novel method for hypersonic flight vehicle’s maneuver flight constrained control [J]. Journal of Northwestern Polytechnical University, 2016, 34(6): 945-950.] [3] Brocanelli M, Gunbatar Y, Serrani A, et al. Robust control for unstart recovery in hypersonic vehicles [C]. AIAA Guidance, Navigation, and Control Conference, Minneapolis, USA, Aug 13-16, 2012. [4] An H, Liu J, Wang C, el al. Disturbance observer based antiwindup control for air-breathing hypersonic vehicles [J]. IEEE Transactions on Industrail Electronics, 2016, 63(5): 3038-3049. [5] Xu B. Robust adaptive neural control of flexible hypersonic vehicle with dead-zone input nonlinearity [J]. Nonlinear Dynamics, 2015, 80(3): 1509-1520. [6] 王鹏飞, 王杰, 罗畅, 等. 高超声速飞行器输入受限反演鲁棒控制 [J]. 控制与决策, 2017, 32(2): 232-238. [Wang Peng-fei, Wang Jie, Luo Chang, et al. Robust back-stepping control of flexible air-breathing hypersonic vehicle subject to input constraints [J]. Control and Decision, 2017, 32(2): 232-238.] [7] Wang F, Hua C C, Zong Q. Attitude control of reusable launch vehicle in reentry phase with input constraint via robust adaptive backstepping control [J].International Journal of Adaptive Control and Signal Processing, 2015, 29(10): 1308-1327. [8] Vaddi S S, Sengupta P. Controller design for hypersonic vehicles accommodating nonlinear state and control constraints [C]. AIAA Guidance, Navigation, and Control Conference, Chicago, USA, Aug 10-13, 2009. [9] Farrell M, Sharma M. On-line approximation based control of uncertain nonlinear systems with magnitude, rate and bandwidth constraints on the states and actuators [C]. 2004 American Control Conference, Boston, USA, Jun 30-Jul 2, 2004. [10] Xu B, Wang S X, Gao D X, et al. Command filter based robust nonlinear control of hypersonic aircraft with magnitude constraints on states and actuators [J]. Journal of Intelligent & Robotic Systems, 2014, 73(1): 233-247. [11] 董朝阳, 路遥, 王青. 高超声速飞行器指令滤波反演控制 [J]. 宇航学报, 2016, 37(8): 957-963. [ Dong Chao-yang, Lu Yao, Wang Qing. Command filtered backstepping control for hypersonic vehicle [J]. Journal of Astronautics, 2016, 37(8): 957-963.] [12] Tee K P, Ge S S. Control of state-constrained nonlinear systems using integral barrier Lyapunov functions [C]. The 51st IEEE Conference on Decision and Control, Hawaii, USA, Dec 10-13, 2012. [13] Ginoya D, Shendge P D, Phadke S B. Sliding mode control for mismatched uncertain systems using an extended disturbance observer [J]. IEEE Transactions on Industrial Electronics, 2014, 61(4): 1983-1992. [14] Parker J T, Serrani A, Yurkovich S, et al. Control-oriented modeling of an air-breathing hypersonic vehicle [J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 856-869. [15] Tee K P, Ge S S, Tay E H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems [J]. Automatica, 2009, 45(4): 918-927. 通信地址:陕西省西安市碑林区友谊西路127号234信箱(710072) 电话:(029)88493113 E-mail: zxfeng@mail.nwpu.edu.cn 郭建国(1975-),男,博士,教授,主要从事先进控制理论等方面的研究。本文通信作者。 通信地址:陕西省西安市碑林区友谊西路127号234信箱(710072) 电话:(029)88493113 E-mail: guojianguo@nwpu.edu.cn Robust Attitude Control Design for a Hypersonic Vehiclewith Multi-Constraints FENG Zhen-xin, GUO Jian-guo, ZHOU Jun (Institute of Precision Guidance and Control, Northwestern Polytechnical University, Xi’an 710072, China) A constrained robust attitude control algorithm is addressed for a hypersonic vehicle with angle of attack constraint, input nonlinearities and uncertainties in this paper. First, the angle of attack constraint issue is properly handled by the integral barrier Lyapunov functions (IBLF) method integrating with the dynamic surface control technique. Moreover, the angle of attack is guaranteed in its constrained set while the “explosion of complexity” is properly avoided. Then, to eliminate the effectiveness of the actuator nonlinearities, a novel auxiliary error compensation design is employed based on the compensated tracking error. In addition, the uncertainties are estimated and compensated by utilizing the nonlinear disturbance observer. Finally, the uniform ultimately boundedness of the closed-loop control system is rigorously ensured by the Lyapunov theorems. The numerical simulation results demonstrate the effectiveness of the proposed method. Hypersonic vehicle; Angle of attack constraint; Input constraint; Barrier function; Disturbance observer 2017- 05- 04; 2017- 06-19 国家自然科学基金(61473226) V448.2 A 1000-1328(2017)08-0839-08 10.3873/j.issn.1000-1328.2017.08.008 冯振欣(1990-),男,博士生,主要从事飞行器制导、控制等方面的研究。
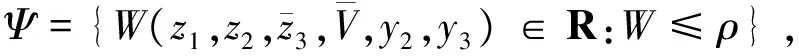
3 仿真校验
4 结 论
