航天器组件高量级冲击环境的一种评估方法

杨新峰, 邹轶群, 邓卫华, 扈勇强, 单悌磊, 张玉梅

(航天东方红卫星有限公司,北京 100094)

航天器组件高量级冲击环境的一种评估方法

杨新峰, 邹轶群, 邓卫华, 扈勇强, 单悌磊, 张玉梅

(航天东方红卫星有限公司,北京 100094)

针对不同冲击响应谱下航天器组件的加速度和应变进行了测量和研究，分析了冲击响应谱频率对冲击力传递的影响，以及组件本身结构频率与冲击力传递的关系，按应变等效准则，提出了一个把组件冲击响应谱转化为冲击试验规范谱的方法。不同冲击响应谱的应变数据验证表明，该方法可以有效地把组件高量级的冲击响应谱转化为低量级的冲击试验规范条件，为航天器组件在高量级冲击下的影响评估和验证提供一条途径。

高量级冲击；冲击响应谱；冲击试验规范；冲击力传递

0 引 言

航天器与运载火箭之间的连接包带爆炸解锁以及航天器本身携带的火工品爆炸解锁会给航天器带来严厉的冲击环境，冲击载荷一般表现为短时瞬态、高频和高量级的特点[1-2]，可对含有敏感器件(如继电器、晶振、微电子芯片等)以及脆性材料的组件造成损伤[3-4]，因此航天器发射前,需要对航天器组件能否承受高量级冲击载荷进行充分的分析和评估。

对冲击的分析和评估可以借助仿真分析和试验的手段。目前，火工冲击过程的仿真分析主要有有限元法、统计能量法、光滑粒子流体动力学法以及Hydrocodes等方法[5-9]，但由于火工冲击的非线性、复杂性，航天器的火工冲击响应的准确建模预示还是比较困难[1,10]，因此在航天工程上，通常通过冲击试验模拟和验证来保证冲击环境下组件的可靠性。鉴于航天器上不同部位的冲击量级和频谱特性差别很大，而实际的冲击响应谱曲线也很难精确地模拟，航天器组件的冲击试验一般按冲击试验规范条件进行[11],冲击试验规范条件中的中高频为平直冲击谱,用此平直冲击谱覆盖组件的冲击响应谱最大量级来考核验证。这种试验方法能基本达到航天器上大部分组件的冲击试验验证要求，但航天器上一些组件尤其处于冲击源近场的组件其冲击响应谱量级很高，可到达4000g以上的高量级，大大超出了一般航天器组件的平直冲击谱规范条件。

对于几千g量级及其以上的高量级冲击不仅地面试验设备能力难以达到,而且以如此高量级的平直谱条件试验模拟也往往超出组件的实际冲击环境影响，表现为中低频的量级超出实际冲击环境，造成过试验，可能带来不必要的损伤。同时，实际环境在高频段的极高量级地面试验一般很难模拟达到，又可能导致高频的欠试验。目前，如何合理的分析评估高量级冲击对组件的影响仍是待研究的问题。美国军用标准(MIL-STD-1540C)[12 ]以及我国军用标准(GJB-1027A-2005)[13]中都给出免做组件鉴定冲击试验的条件之一为2000 Hz以上所有频率的最大期望冲击谱的加速度g值小于0.8乘以频率的值，表明了2000 Hz以上高频冲击影响可以某种程度上忽略。俞佳江等[14]把基于冲击响应谱峰值计算而来的最大位移作为评估单机所受冲击响应的程度，通过某卫星高量级冲击实测数据的位移计算，认为虽然此卫星地面冲击试验量级(平直谱800g)小于星上冲击响应谱最高加速度量级，但按位移估算此卫星地面冲击试验能覆盖星上产品所受的高量级冲击环境。这说明星上高量级冲击谱产生的冲击作用可能没有那么大,以地面冲击试验覆盖星上最大冲击量级有可能带来超出实际的过分严厉考核。冲击试验与实际冲击环境的差异也说明冲击环境下的载荷作用机理还没十分清楚，还不能精确地为冲击试验提供依据。那么，星上高量级冲击响应谱对组件的作用如何评估，它等价于多大的地面冲击试验规范条件？本文通过试验测试和数据分析，研究提出一种把高量级冲击响应谱转化为地面冲击试验规范谱的方法，为航天器组件地面冲击评估与验证提供依据。

1 冲击响应谱的频率影响分析

航天器的冲击试验与分析通常以冲击加速度计量，尤其以冲击响应谱的最大加速度量级来判别冲击的严厉程度，然而，冲击对组件的作用还是通过组件安装界面的力传递的，因此，分析冲击下的组件应变规律可以研判冲击传递给组件的力大小，进而可以分析频率对冲击力传递的影响。为具体观测冲击谱不同频率下的应变特性，模拟常见航天设备的动态特性，设计试验组件，如图1所示，质量约5.5 kg，试验测试得到其一阶横向频率约为280 Hz。使用此组件进行不同冲击谱的冲击试验，在组件根部粘贴应变片，在组件安装处安装加速度计，分别测量冲击试验中的应变和加速度。

图1 冲击试验中的试验件Fig.1 Test specimen in shock testing

为定性分析冲击频谱对组件应变的作用,从组件多次冲击试验中选取冲击响应谱最大加速度量级相近的冲击工况进行分析。图2为组件两次冲击(工况 c1h-d400-1和工况c1h-shoudong-2)的加速度响应谱的对比，两工况冲击试验的冲击响应谱最大量级相当，都为840g左右，对应频率在6500 Hz～7500 Hz。但在1000 Hz以下工况 c1h-d400g-1的冲击加速度量级明显高于工况 c1h-shoudong-2的冲击加速度量级，在525 Hz处冲击量级相差约25 dB。在两工况冲击下，组件根部的应变时域值大小比较见图3。可见两次冲击的应变大小差别很大，工况c1h-d400g-1冲击的应变幅值约为700微应变，工况c1h-shoudong-2冲击的应变幅值约为70微应变，大约相差10倍。两次冲击的冲击谱最大加速度相当但应变差异较大，说明冲击产生的力与频率相关，并不单由最大冲击响应加速度量级确定。按最大冲击响应量级[14]的位移来考核冲击的严厉程度还不全面。

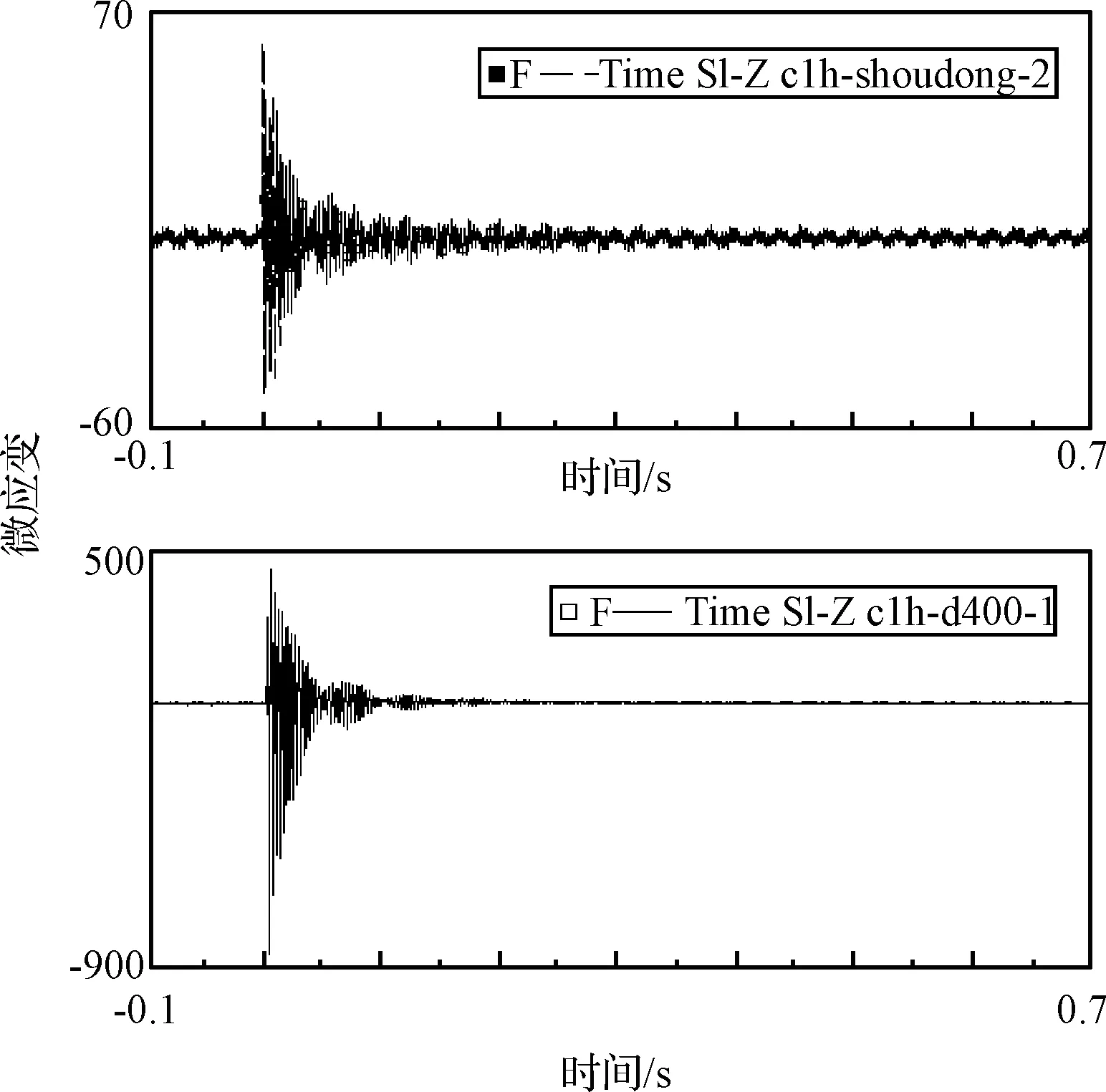
图3 工况c1h-d400-1和工况c1h-shoudong-2冲击应变Fig.3 Shock strain values for case c1h-d400g-1 and case c1h-shoudong-2

组件的多次冲击中， 工况c1h-shoudong-1和工况 c1h-shoudong-2两次冲击响应谱最大加速度量级不同，但两工况3000 Hz以下(A1测点)的冲击响应谱相当(见图4)，其中3000 Hz以上冲击响应谱最大量级分别约为840g和414g，相差426g(大约2倍)。然而，工况c1h-shoudong-1和工况 c1h-shoudong-2的两次冲击中应变大小相当(见图5)，应变的时域最大值分别为58微应变和50微应变。这说明应变主要由低频冲击响应引起， 冲击中的高频响应引起的应变与力较小。

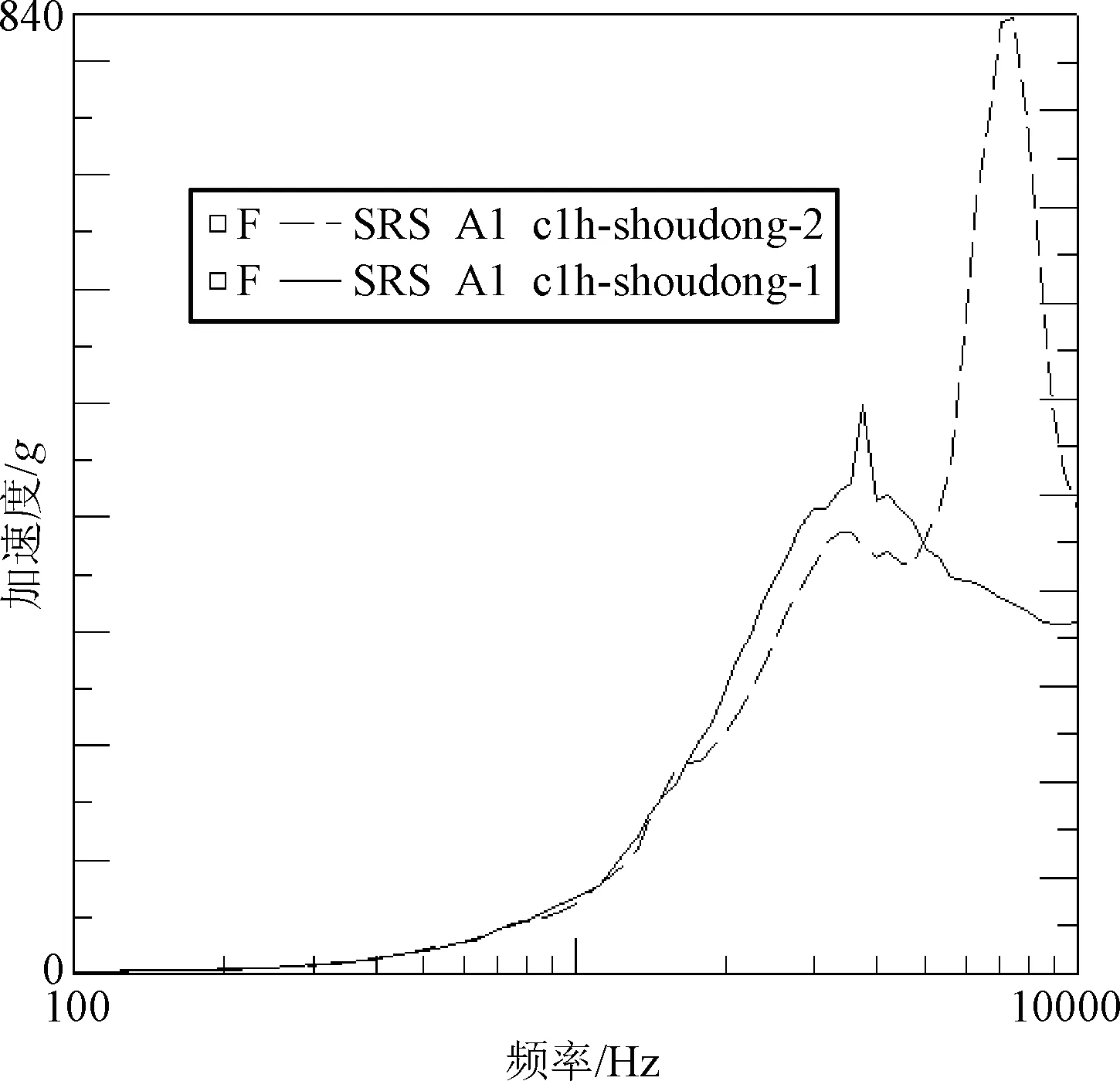
图4 工况c1h-shoudong-1和工况c1h-shoudong-2 冲击响应谱Fig.4 Shock response spectrums for case c1h-shoudong-1 and case c1h-shoudong-2

对冲击下组件的应变进行进一步分析发现，应变响应与组件结构主频率相关，以工况 c1h-d400-1冲击为例，其应变的傅立叶变换如图6所示，可以看出，应变在组件主频率280 Hz处具有较大的值，即组件共振区域是应变的主要贡献者。在组件冲击试验中，组件上应变是通过撞击基础带动组件突然运动而引起的，基于位移与应变的相关性，其冲击位移也会在组件共振区域最大。

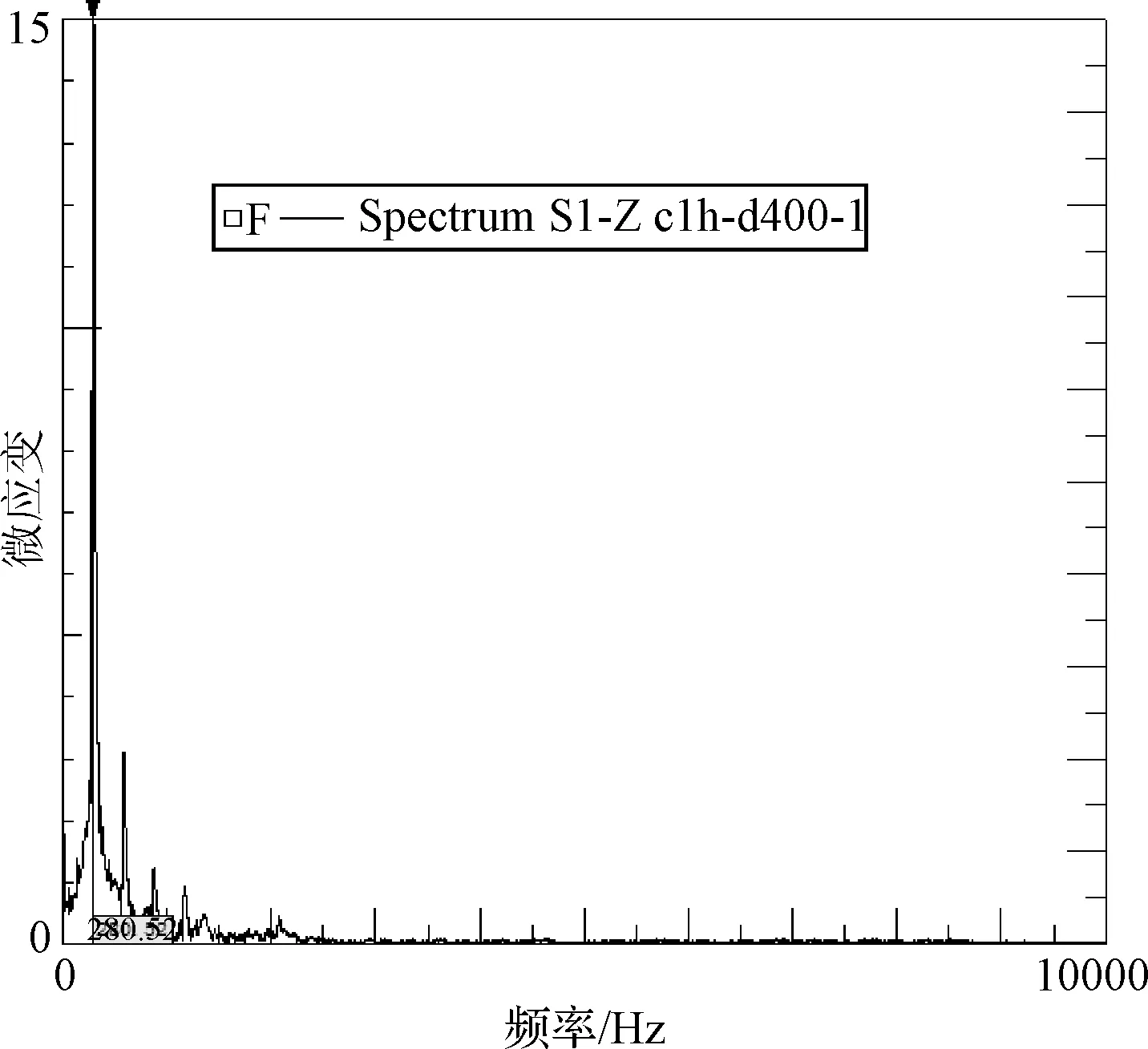
图6 工况 c1h-d400-1冲击应变的傅立叶变换谱Fig.6 Fourier transform of shock strain for case c1h-d400-1

上述分析说明，冲击响应谱的加速度量级在高频段可能很高，但并不产生较大的变形，意味着高频段冲击谱不传递较大的冲击力，而低频段冲击响应谱将会产生较大的变形，表明低频段冲击谱对组件传递较大冲击力，尤其在组件一阶主频率处产生较大冲击力。

2 冲击响应谱与试验规范条件的等价分析

2.1 基于频率的冲击响应谱转换分析

组件上应变大小反映了冲击对组件作用大小。数据分析说明冲击产生的力并不单由最大冲击响应量级确定，高频处的冲击加速度量级比较大，但冲击应变及力并不大。应变及力主要由低频段冲击响应引起，冲击中应变与力随着频率增高而减小。冲击的作用表现为频率与量级的综合作用。

为反映频率的影响规律，把组件冲击加速度响应谱除以频率的平方，转换为位移的量纲。根据冲击响应谱的定义，这个位移不是组件的真实位移，本文称之为转换位移，用以描述冲击下位移的大小程度。那么，组件冲击加速度响应谱的转换位移为

(1)

式中:S为冲击加速度响应谱，随频率f而变化。

根据组件冲击试验的应变响应特性，上述转化位移也同样会在组件一阶主频处最大。对于很多航天器组件，一阶模态是组件的主导模态，可以简化为按单一主模态组件处理。对于单一主模态组件，转化位移可以借用振动响应中的放大因子Q来考虑一阶主模态频率的影响。那么，考虑组件主模态频率影响的冲击加速度响应谱的转换位移为

(2)

对全频段的转换位移进行求和，得到组件冲击加速度响应谱的累计转换位移

(3)

式中:Dr为由冲击加速度响应谱计算而来的累计转换位移。求和的频率范围由冲击响应谱处理的最低和最高频率决定，一般为100～10000 Hz。累计转换位移与组件冲击形变相关联，累计位移大则冲击形变大，即冲击作用力大。

根据以上转换公式，相比于冲击加速度响应谱，冲击转换位移或累计转换位移也考虑了高频的影响，但高频的影响减小了。

2.2 试验规范条件的转换分析

航天器组件冲击试验一般按冲击试验规范条件[11,15]进行。冲击试验规范条件见图7，规范中低频段范围为f1～f2,Φ1为低频段上升斜率，常见为+6 dB/oct，规范的中高频段范围为f2～f3,是规范中主要频段，为平直谱，因此这种冲击试验规范条件又可称为平直谱条件。航天器冲击试验规范条件的平直段量级一般为一定值，如多数卫星以平直段量级1000g对卫星组件进行冲击鉴定试验(即Φ2=1000g)。

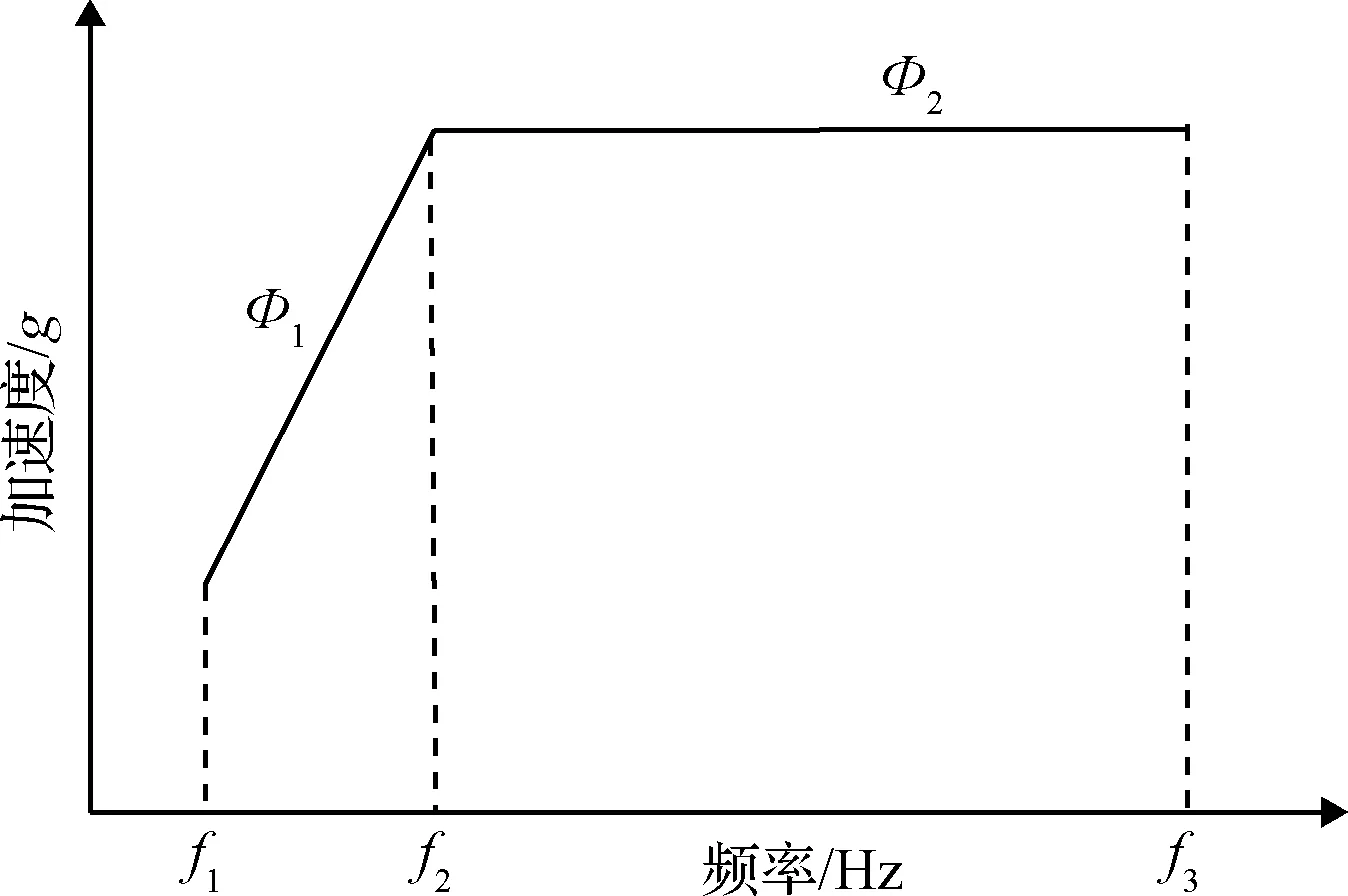
图7 冲击试验规范条件Fig.7 Shock test standard specification

若冲击试验规范条件中的低频段某频率f的量级为Φi，它与平直段Φ2的关系为

(4)

有

(5a)

因此给定平直谱量级即可确定整个冲击试验输入谱。一般Φ1=6，则频率f1-f2之间的冲击谱量级为

(5b)

鉴于冲击试验规范条件也是加速度谱，可按上述同样方法把组件冲击试验规范条件转化为累计转换位移

(6)

Dt为由冲击试验规范条件计算而来的累计转化位移，Φ2为冲击加速度试验规范的平直谱量级。型号文件中，f1一般为100 Hz，f3一般为4000 Hz，目前，f2的值在各型号中不完全相同(如600 Hz、800 Hz等)，具体根据型号规定而定。

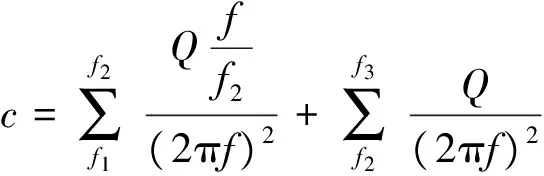
Dt=Φ2c

(7)

2.3 等价关系公式

航天器上的组件冲击响应谱用地面规范条件验证或评估时，可以以产生的累计转化位移相等来等效，也相当于冲击中传递的力等效。因此，把式(3)和式(7)相等，得到与冲击响应谱等效的冲击加速度试验规范的平直谱量级

(8)

式(8)把组件实际经历的冲击响应谱S可以等价于一定量级的冲击试验规范条件。以冲击工况c1h-03mp-a1为例，其冲击测试得到冲击响应谱如图8所示，最大量级约为4505g，最大量级的频率约在6684 Hz，并且630 Hz以后都大于1000g。用式(8)等效后，计算得到工况c1h-03mp-a1冲击响应谱的等效冲击试验规范条件为978.5g。此量级远小于冲击响应谱最高量级4505g，等效后的冲击输入谱量级以及谱型和误差要求则是试验设备能力和试验控制技术能够达到的和保证的。基于试验规范条件的冲击试验是航天器组件经常开展的地面冲击验证试验，航天组件及其零部件在规范试验条件下的冲击规律和效应也累积了大量经验与数据，设计师具有对规范冲击的设计经验和基础。高量级的响应谱如果能与冲击规范试验条件建立联系，则为航天器组件在高量级冲击下的影响评估和验证提供一条途径。

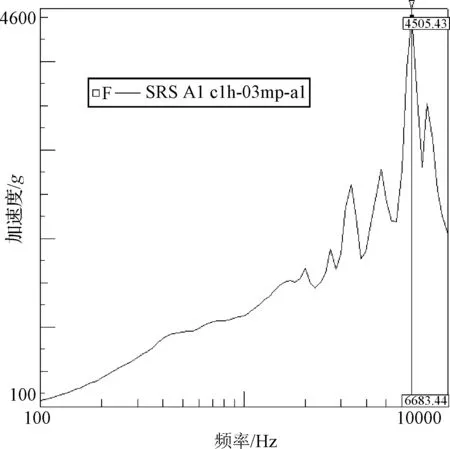
图8 工况c1h-03mp-a1冲击响应谱Fig.8 Shock response spectrum for case c1h-03mp-a1

冲击等效式(8)是基于一阶模态为主的结构件冲击响应规律得到的，对于分散模态的结构件及其不同模态频率处的冲击响应特性本次研究测试还没有涉及,因此上述的高量级冲击等效公式主要适用于单一模态为主的航天器组件。

冲击产生的作用与影响有多种，较大的冲击载荷可能造成结构或材料的断裂破坏，或者材料发生了塑性变形。然而，在航天器火工品解锁带来的冲击环境中，冲击载荷引起的结构破坏比较少见[1,16]，主要是引起航天器组件中的元器件等部件的失效，一般是电性能的失效。对于元器件级的冲击破坏机理研究的报导还比较少，有待进一步研究。然而，分析传递至元器件的冲击载荷大小与特性可帮助开展元器件冲击失效机理的研究。因此，探索航天器冲击载荷的传递特性，逐步确定至元器件的冲击载荷及其频谱特性是重要的和必要的。本文从组件级别上分析航天器冲击载荷的传递特性，为进一步研究元器件冲击失效机理提供了基础。

3 验证分析

利用试验件开展了6次不同冲击谱的验证测试，这6次冲击工况的冲击响应谱如图9所示。其中工况c1h-d400-1拐点约在600 Hz，谱型较平，近似于冲击规范条件488g的冲击试验，代表试验量级488g的平直谱条件。其他工况均在某些频点存在较大峰值，与星上火工品解锁设备处的冲击响应谱近似。

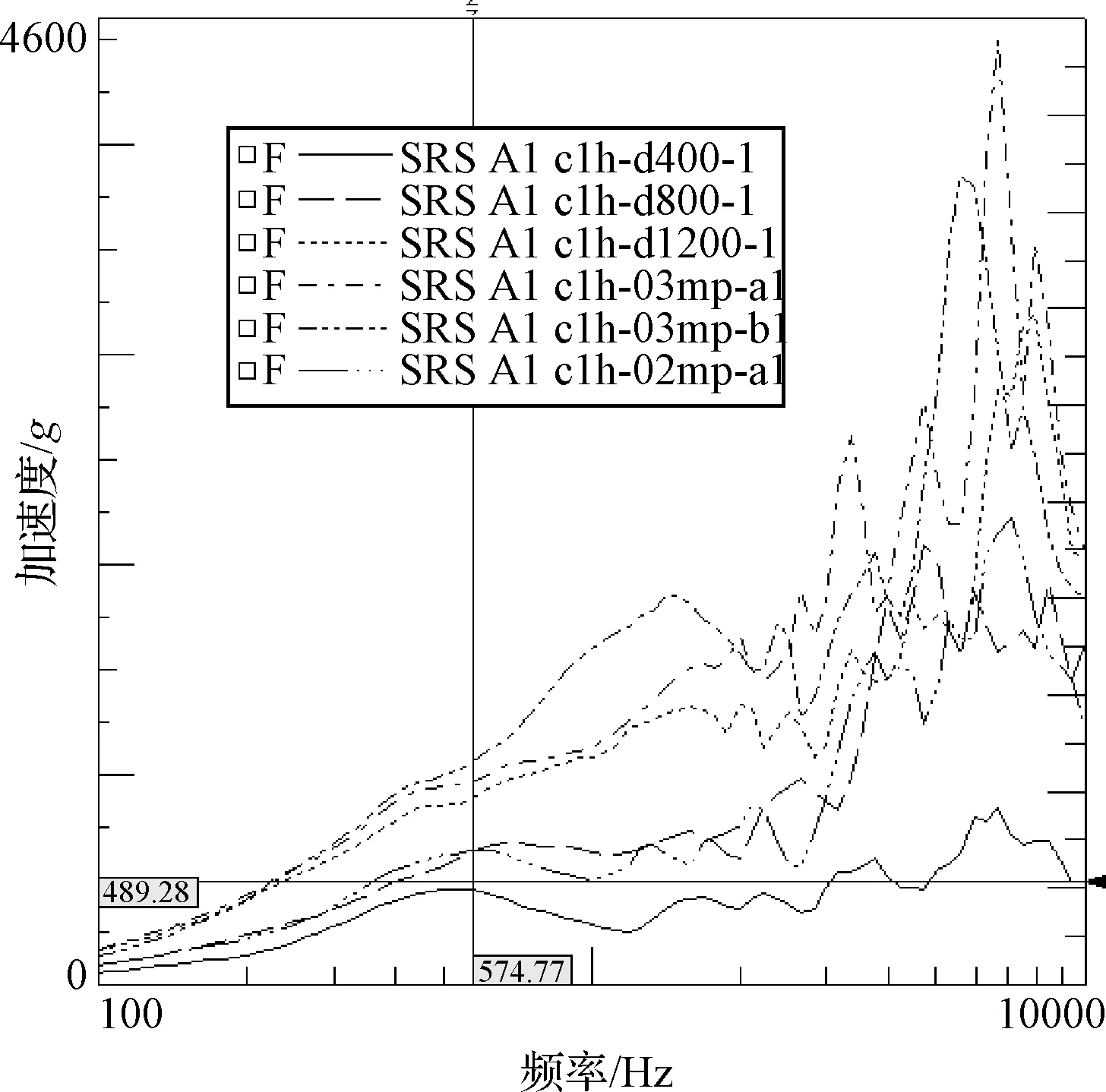
图9 6次冲击工况的冲击响应谱Fig.9 Shock response spectrums for 6 shock test cases

以工况c1h-d400-1试验量级488g作为基准，把其它工况的应变与工况c1h-d400-1的应变相比，则可得到基于应变的各工况冲击规范量级。例如，某一工况冲击的应变是工况c1h-d400-1的应变的2倍，则此工况的冲击规范试验量级为488g的2倍，即976g。

6次冲击的测得时域应变见图10，各工况的冲击应变平均幅值见表1。其中，工况c1h-d400-1冲击在组件上的产生应变为-533.73～611.46微应变，平均幅值为572.6微应变。那么根据实测应变幅值得到的6次冲击的冲击规范量级见表1。

利用等效式(8) 计算得到的组件各冲击工况的冲击规范量级与基于应变的冲击规范量级的比较见表2。可以看到，由等效公式计算得到的各冲击工况的冲击规范量级与基于测试应变的冲击规范量级比较接近，规律符合。在冲击试验规范条件中，允差要求为±6 dB，使用等效公式计算的结果误差最大为2.2 dB，验证了等效公式计算的合理可行性。

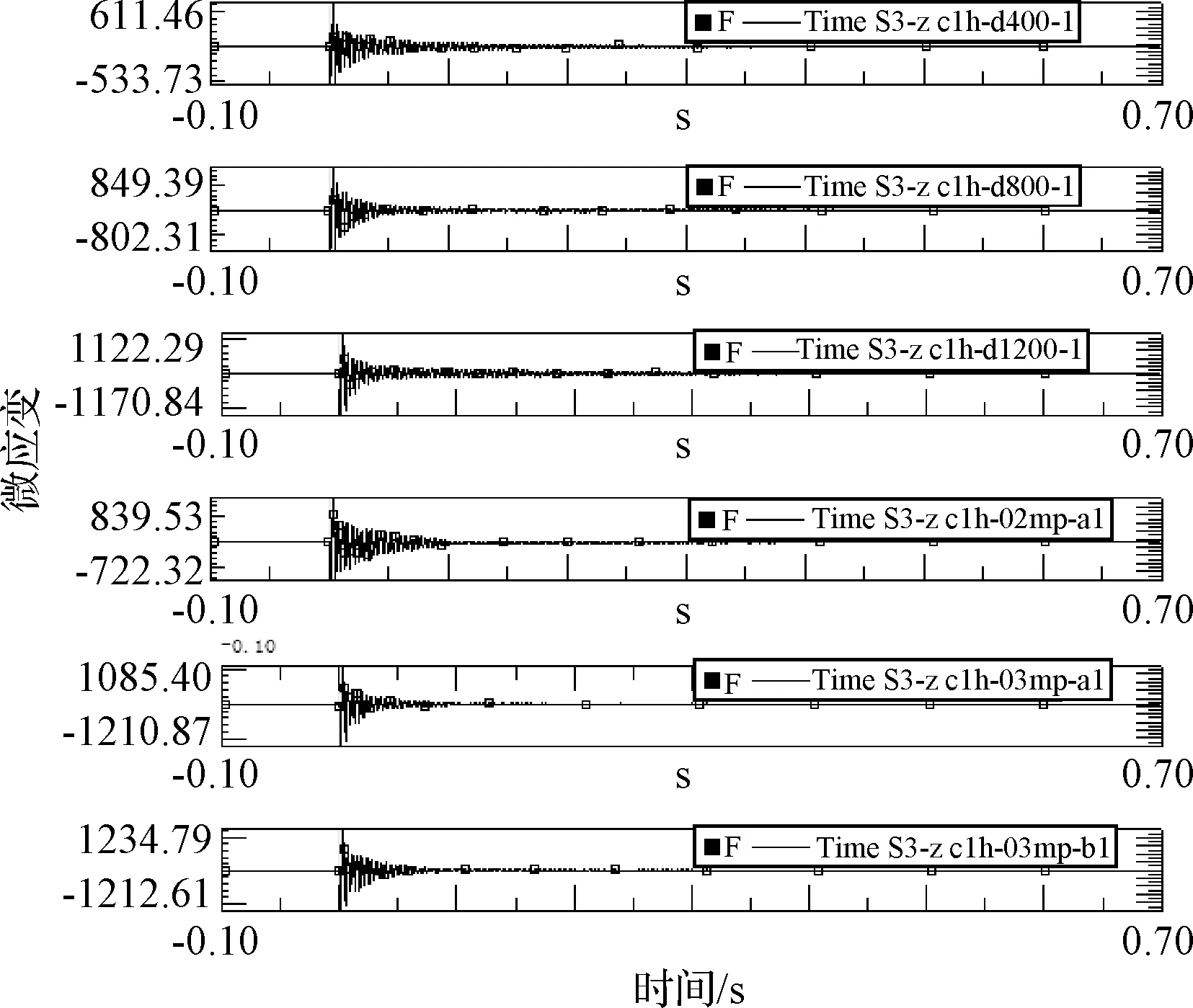
图10 6次冲击工况的冲击应变时域值Fig 10 Shock strains for 6 shock test cases

实际的航天器高量级冲击环境一般表现为在高频段的高量级，利用地面冲击模拟试验基本可以达到在高频段激励出高量级，但很难完全模拟实际的冲击响应曲线[17]。地面冲击模拟试验中，低频段的量级往往随着高频段量级的提高而相应提高，因此。对于一些高频段量级较高而低频段量级又特别低的实际冲击环境，本次地面冲击试验还无法对其冲击等效的结果进行验证。在冲击等效公式中，低频段发挥重要作用，低频段量级极低的冲击曲线经过等效后，可能远低于一般航天器组件的规范冲击量级。对于这种情况，建议低频段量级极低的冲击环境在低频段f1～f2采用与验收级冲击规范条件相同的量级进行等效，以保证等效冲击量级有充分可信的余量。

表1 各冲击工况下的应变幅值及基于应变的冲击规范量级

表2 各冲击工况下式(8)等效的冲击规范量级与基于应变的冲击规范量级的比较

4 结 论

本文数据分析表明，航天器组件冲击载荷的传递与频率相关，低频段冲击响应谱将会对组件传递较大冲击载荷，同时冲击载荷传递与组件结构频率相关，对类似单一模态的结构，主要在结构一阶频率处产生较大冲击载荷。

根据数据分析结果，按冲击应变等效的原则提出一个把组件冲击响应谱转化为试验规范类型的冲击谱的方法。该方法考虑了组件冲击传递中冲击载荷随频率变化的规律，以及组件一阶模态对组件冲击的作用影响，转化后的试验规范量级经不同冲击谱下的应变结果所验证。该方法可以有效降低某些频点具有较大量级的冲击响应谱，能够与航天器组件常用的冲击试验规范条件进行比较评估，利于高量级的冲击响应在冲击台进行试验验证。

鉴于本文是对一阶模态占主导的组件所给出测试结果和分析，因此，本文的冲击等效公式适用于一阶模态为主的航天器组件。对于复杂航天器组件，其模态可能比较分散，冲击载荷与模态的关系还需作进一步测试分析。

[1] 丁继锋,赵欣,韩增尧.航天器火工冲击技术研究进展[J].宇航学报，2014, 35(12):1339-1349.[Ding Ji-feng, Zhao Xin, Han Zeng-yao. Research development of spacecraft pyroshock technique [J].Journal of Astronautics,2014, 35(12): 1339-1349.]

[2] 毛勇建,李玉龙.爆炸分离冲击环境的模拟试验技术进展[J].导弹与航天运载技术，2007(4):37-44. [Ma Yong-jian, Li Yu-long. Advances in simulation techniques of pyroshock environments [J]. Missile and Space Vehicle, 2007(4):37-44.]

[3] 张欢,刘天雄,李长江,等. 航天器火工分离螺母的火工冲击环境数值仿真研究[J]. 航天器环境工程，2014,31(4):363-368. [Zhang Huan, Liu Tian-xiong, Li Chang-jiang, et al. Numerical simulation of pyrotechnic shock environment concerning pyroshock separation nut of spacecraft [J]. Spacecraft Environment Engineering, 2014, 31(4):363-368.]

[4] 张建华.航天产品的爆炸冲击环境技术综述[J].导弹与航天运载技术，2005(3):30-36.[Zhang Jian-hua. Reviews on pyroshock environment of aerospace equipment[J]. Missile and Space Vehicle, 2005(3):30-36.]

[5] Lee J R，Chia C C，Kong C W．Review of pyroshock wave measurement and simulation for space systems [J]．Measurement，2012(45)：631-642．

[6] Iwasa T, Shi Q, Ando S, et al. Simplified SRS prediction method for pyroshock source of v-band clamp separation devices[C]. The 48thAIAA/ASME/AHS/ ASC Structures, Structural Dynamics and Materials Conference, Honolulu, Hawaii, USA, April 23-26, 2007.

[7] Li J, Yan S, Tan X. Dynamic-envelope analysis of clamp-band joint considering pyroshock of satellite separation [J].Journal of Spacecraft and Rockets, 2014, 51(5): 1390-1400.

[8] 许庆新.基于SPH方法的冲击动力学若干问题研究[D].上海：上海交通大学，2009.[Xu Qing-xin. Study of some impact dynamics problems based on smoothed particle hydrodynamics method [D]. Shanghai: Shanghai Jiao Tong University,2009.]

[9] 张帆. 物质点法在冲击动力学中的应用研究[D]. 哈尔滨：哈尔滨工程大学，2012. [Zhang Fan. Study on application of material point method in shock dynamics [D].Harbin: Harbin Engineering University,2012.]

[10] 赵欣，韩增尧，邹元杰，等.一种航天器火工冲击源建模和分析方法[J].宇航学报,2015,36(10):1210-1218.[Zhao Xin,Han Zeng-yao, Zou Yuan-jie, et al. A feasible method for modeling and analyzing the pyroshock source of spacecraft[J].Journal of Astronautics, 2015, 36(10): 1210-1218.]

[11] 卢来洁,马爱军,冯雪梅. 冲击响应谱试验规范述评[J].振动与冲击,2002,21(2):18-21.[Lu Lai-jie, Ma Ai-jun,Feng Xue-mei. A review of shock response spectrum test standard [J]. Journal of Vibration and Shock，2002,21(2):18-21.]

[12] MIL-STD-1540C,Test requirements for launch, upper-stage, and space vehicles[S].

[13] GJB-1027A-2005,运载器、上面级和航天器试验要求[S].

[14] 俞佳江,韦锡峰,肖文斌.位移损伤判据在卫星冲击试验中的应用[J].上海航天，2014，31(Z)：95-97,139.[Yu Jia-jiang, Wei Xi-feng, Xiao Wen-bin. Application of displacement damage criterion in satellite shock test[J]. Aerospace Shanghai,2014，31(Z)：95-97,139.]

[15] 何文杰.冲击试验条件等效性及其转换方法的研究[D].上海：复旦大学，2012.[He Wen-jie. Research of conversion and equivalence of shock test specification[D].Shanghai: Fudan University, 2012.]

[16] Gentz S J, Ordway D O, Parsons D S, et al. Empirical model development for predicting shock response on composite materials subjected to pyroshock loading[R]. NESC-RP-12-00783, Langley Research Center, Hampton, Virginia, USA, July 2015.

[17] Houshmand B, Lacher A, Juengel N, et al. A novel excitation method for pyroshock simulation[J]. Journal of Vibration and Control, 2016, 22(20): 4247-4258.

通信地址: 北京海淀区友谊路104号航天东方红 (100094)

电话:13520154957

E-mail: yangfzw@sina.com

An Approach to Evaluate High Level Shock for Aerospace Units

YANG Xin-feng, ZOU Yi-qun, DENG Wei-hua, HU Yong-qiang, SHAN Ti-lei, ZHANG Yu-mei

(DFH Satellite Co. Ltd, Beijing 100094, China)

The acceleration and strain for an aerospace unit under different shock response spectrum excitations are measured and studied. The influence of the frequency of the shock response spectrum on the shock force transmission is analyzed as well as the influence of the structural frequency of the unit on the shock force transmission. Based on the analysis results, a method to convert the shock response spectrum into the shock test standard spectrum is proposed which would result in tantamount strain. The strain data from the different shock response spectrum tests shows that the method could transform the high level shock response spectrum into the low level shock test standard spectrum, and would provide a way for the evaluation and verification of the high level shock for aerospace units.

High level shock; Shock response spectrum; Shock test standard; Shock force transmission

2017-03-01;

2017-05-22

V416

A

1000-1328(2017)08-0872-07

10.3873/j.issn.1000-1328.2017.08.012

杨新峰(1966-)，男，博士，研究员，主要从事航天器动力学分析、大型试验等。