非合作目标接近与跟踪的低复杂度预设性能控制
2017-09-12殷泽阳罗建军魏才盛袁建平
殷泽阳,罗建军,魏才盛,袁建平
(1. 西北工业大学航天学院,西安 710072;2. 航天飞行动力技术重点实验室,西安 710072)
非合作目标接近与跟踪的低复杂度预设性能控制
殷泽阳1,2,罗建军1,2,魏才盛1,2,袁建平1,2
(1. 西北工业大学航天学院,西安 710072;2. 航天飞行动力技术重点实验室,西安 710072)
针对追踪航天器接近和跟踪非合作目标任务中的相对位姿控制问题,基于预设性能控制理论提出一种低复杂度预设性能控制方法(LCPPC)。该控制方法一方面无需对模型的具体参数(如追踪航天器与非合作目标的质量、惯量参数等)进行先验估计或在线辨识,另一方面又能预先设计系统的瞬态和稳态性能,保证相对位姿控制系统在存在外部干扰、不确定性和非合作目标不可测机动的条件下仍能满足预先设计的性能要求。仿真结果表明,该控制方法能够在未知系统参数的条件下,实现非合作目标交会任务的快速实时高精度控制。
预设性能控制;非合作目标;无模型;低复杂度;鲁棒控制
0 引 言
自主空间交会是对目标进行在轨服务的前提,也是当前空间技术领域的研究热点。随着空间技术的不断发展,针对空间非合作目标的在轨服务任务引起了学者的关注。2016年,国家自然科学基金委员会[1]将“空间翻滚目标捕获过程中的航天器控制理论与方法”列为国家自然科学基金重大项目,充分证明了针对非合作目标的接近、跟踪和在轨服务是我国航天领域未来发展的重大需求,具备重要的理论及工程意义。
由于非合作目标具有外形与动力学参数的先验信息少、缺少合作标识、可能存在翻滚、信息层面不沟通、机动行为不配合等特点,其交会轨迹规划与控制需要综合考虑交会过程中的不确定性、目标运动特性与后续操作的精度需求[1-4]。针对非合作目标接近与跟踪问题,陈统等[3]建立了基于视线坐标系的姿轨联合运动模型,并结合模糊控制理论的鲁棒性克服非合作目标所带来的不确定性。高登巍等[4]则将视线跟踪模型与最优控制理论相结合,利用θ-D方法求解非线性最优控制,实现高精度非合作目标接近与跟踪。姜博严等[5]将自适应滑模控制方法引入交会对接过程的姿轨控制中,并在控制器设计中考虑了输入饱和问题。基于预测控制理论,Weiss等[6]提出了一种具有避障功能的空间交会模型预测控制方法。郭永等[7]则基于蔓叶线与人工势场法提出了一种非合作目标安全交会的姿轨联合控制方法。冯丽程等[8]将人工势场法与有限时间控制方法相结合,提出具有动态避障功能的交会控制方法。朱战霞等[9]从建模的角度入手,利用螺旋理论对相对姿轨运动进行耦合建模,并提出了一种姿轨耦合同步控制律。值得注意的是,上述控制方法均依赖于精确的系统模型和参数,是“模型依赖”的控制方法。而在实际工况中,由于非合作目标缺乏合作测量标识,测量结果存在较大的不确定性;追踪航天器在进行多次变轨接近非合作目标的过程中,其质量和惯量矩阵也因燃料消耗和液体晃动存在一定的变化;非合作目标还可能存在难以测量的机动(如逃逸行为等)。因此基于精确模型提出的控制方法在实际工况中很难获得理想的效果。除此之外,非线性最优控制和模型预测控制等方法计算复杂度较高,难以满足在线控制的需求。
在非线性控制领域,近期有学者提出了一种无模型的预设性能控制方法[10-12]。该控制方法仅依赖系统的状态反馈设计控制器,并能够预先设计状态量的收敛轨迹边界,而该边界约束又能够通过非线性映射函数进行无约束化处理。相比于传统控制方法,该方法的优势如下:首先,该控制方法无须对系统模型的具体参数进行先验估计或在线辨识,具有“无模型”的特征。此外,该方法还能预先设计系统的稳态和瞬态性能,保证系统状态按照期望的性能收敛于期望值。再者,该方法也不存在耗时严重的迭代计算、参数辨识等过程,是一种低复杂度的、适合在线计算的控制方法。由于具有上述优势,该控制方法一经提出就得到了控制领域内的极大关注,并成功应用于机器人关节位置与速度跟踪[13]、高超声速飞行器[14-15]等对象中,并取得了良好的控制效果。
本文针对非合作目标接近与跟踪任务,区别于传统模型依赖的控制方法,探索一种不依赖模型参数的鲁棒控制方法。首先,针对姿轨相对运动模型与控制方法不匹配的问题,本文将视线坐标系下航天器相对轨道与姿态跟踪模型进行坐标变换,转化为一种直接反馈形式。接着设计用户可调的预设性能边界,规定系统变量收敛的稳态和瞬态性能。进而构造广义状态变量,提出了基于无模型控制理论的预设性能控制方法,在未知系统参数(如追踪航天器与非合作目标的质量、惯量矩阵等)的前提下实现了非合作目标高精度接近和跟踪。随后证明了广义状态变量和系统状态量在控制器的作用下均处于预设范围内。最终设计仿真试验,对比该控制方法与PID控制方法和基于非线性最优控制的θ-D方法的控制性能。
1 相对运动建模与转化
1.1 相对轨道运动建模[3-4]
视线坐标系下相对轨道运动动力学模型为
(1)
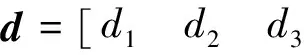
设追踪航天器与非合作目标的最终相对距离为ρf,追踪航天器的期望视线倾角qεd和期望视线偏角qβd可由下式计算得到[4]
(2)
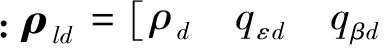
1.2 追踪航天器姿态运动建模
基于四元数的追踪航天器姿态运动学方程为[16]
(3)
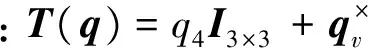
追踪航天器的姿态动力学方程为
(4)
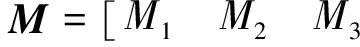
追踪航天器的期望姿态应综合考虑非合作目标的位置和太阳光线的入射方向。不妨令其本体坐标系的xbcf轴为观测设备的中心轴线,太阳能帆板沿追踪航天器的ybcf轴安装。假设太阳光线的入射方向为χ,则追踪航天器的期望空间姿态为
(5)
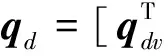
1.3 相对运动模型转化
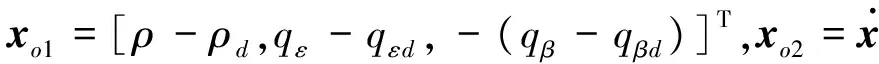
(6)
式中:
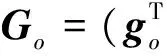
(7)
式中:
ga=(1/2)T(q)J-1
2 无模型预设性能控制
2.1 预设性能的概念
在设计控制器时,往往期望状态量能以较快的速度(如指数速度)收敛于其期望轨迹;在收敛的过程中状态量也不能出现过高的超调量;此外,在稳态过程中,状态量在干扰的作用下应能始终保持有界。因此,如图1所示,若能合理地为状态量设计其收敛轨迹的边界,并设计控制器保证该状态量严格在边界以内收敛,就能保证系统状态在瞬态和稳态的性能[12]。
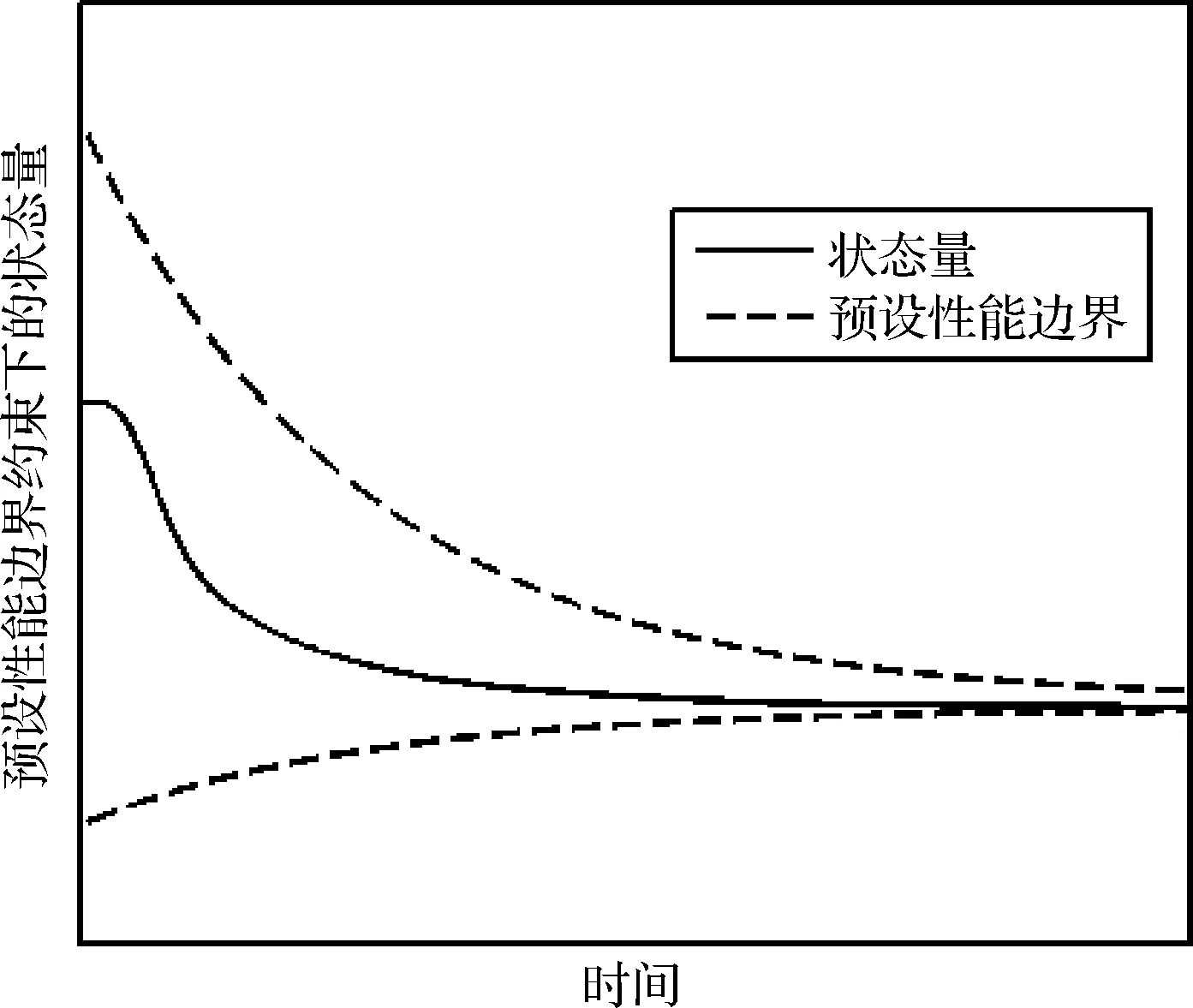
图1 预设性能边界约束下状态量示意图Fig.1 Illustration of the state under prescribed performance function
预设性能边界主要包含三方面的约束,即指数收敛速度、超调量和稳态误差边界。首先考虑指数收敛速度和稳态误差边界。定义如下所示严格递减的正值预设性能函数
α(t)=(α0-α∞)exp(-βt)+α∞
(8)
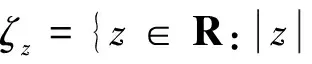
为考虑超调量问题,利用式(8)定义的预设性能函数,可规定如下所示的预设性能边界
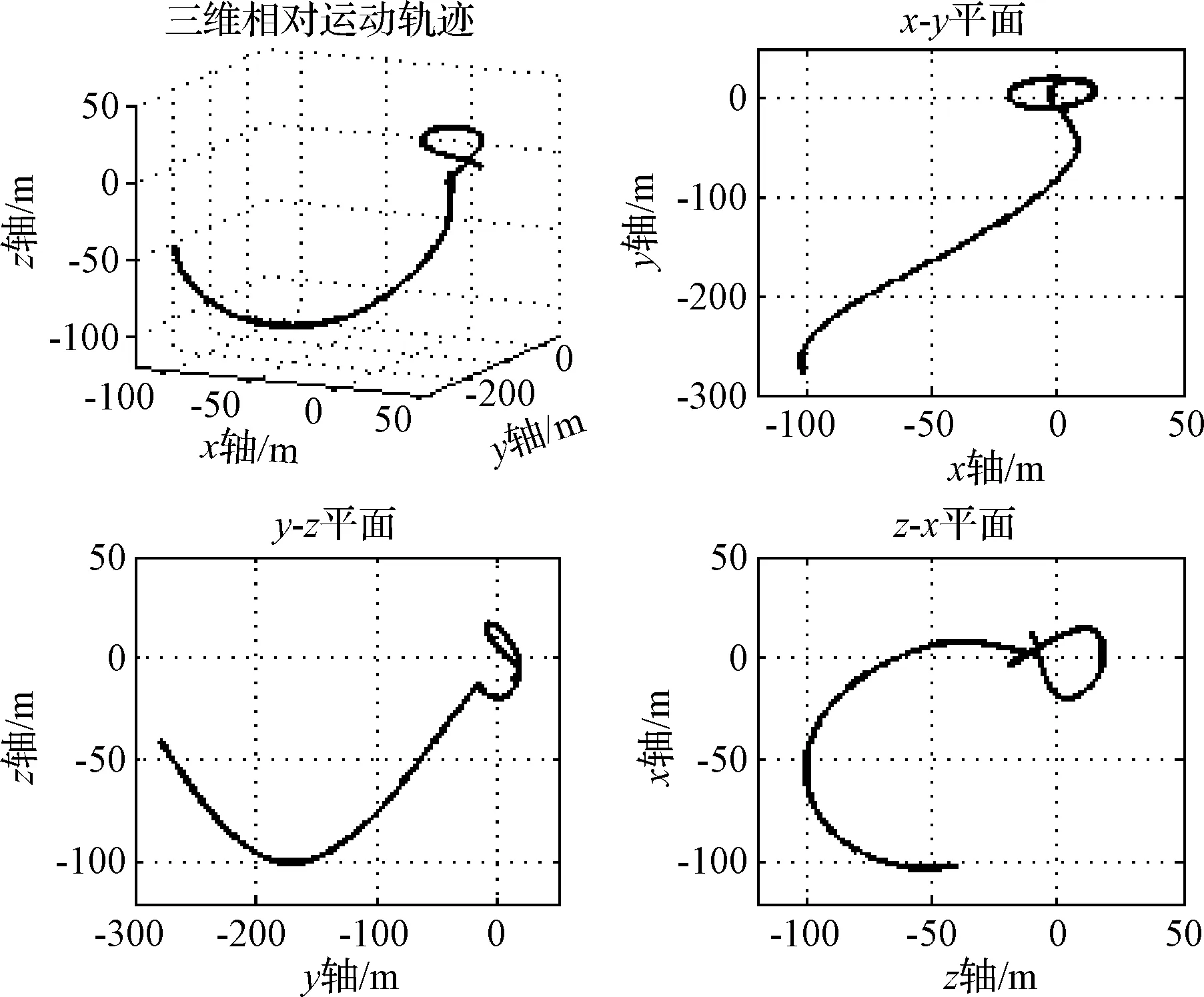
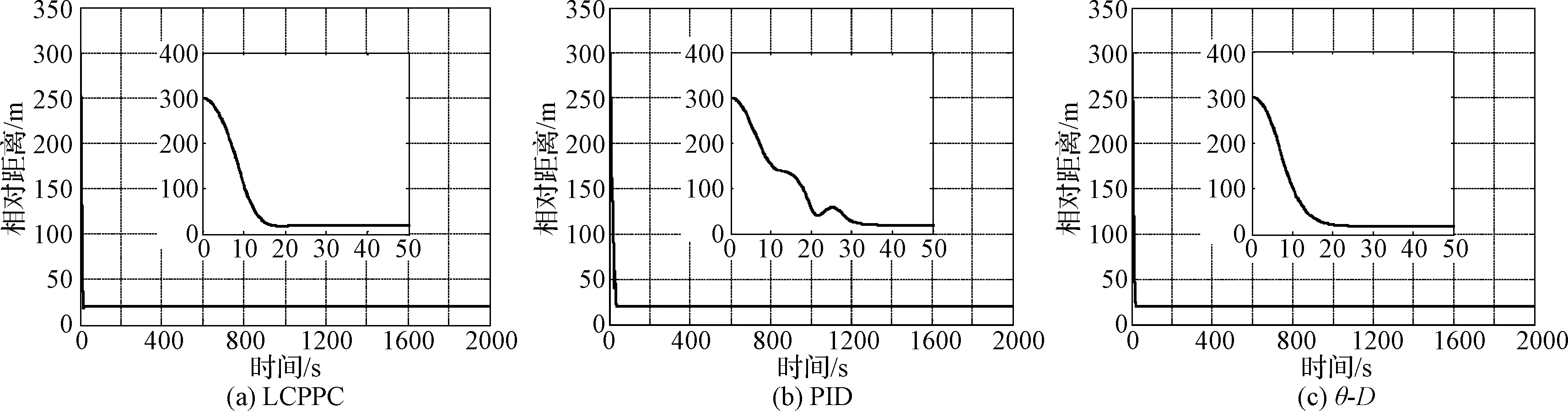
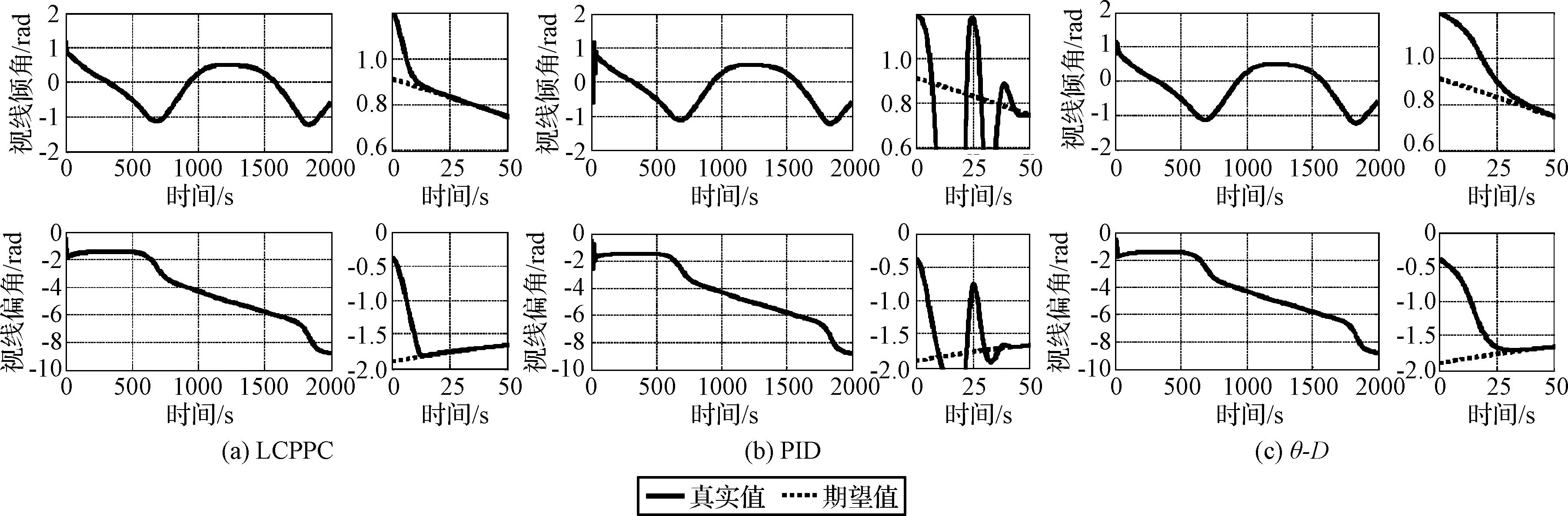
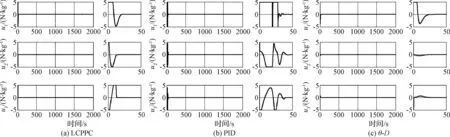
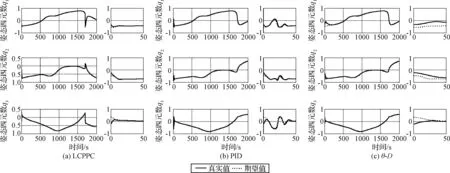
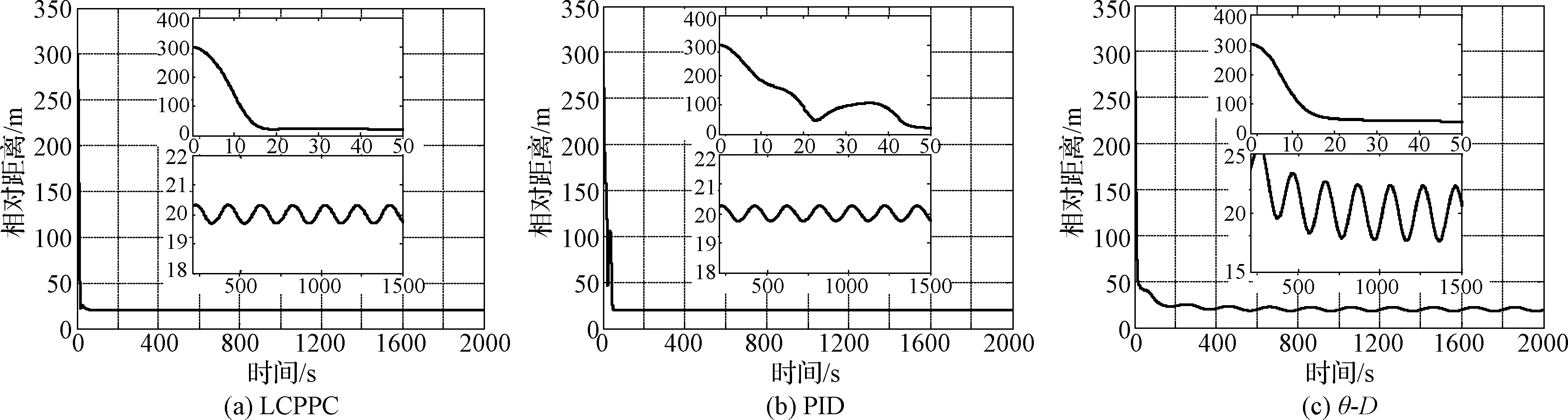
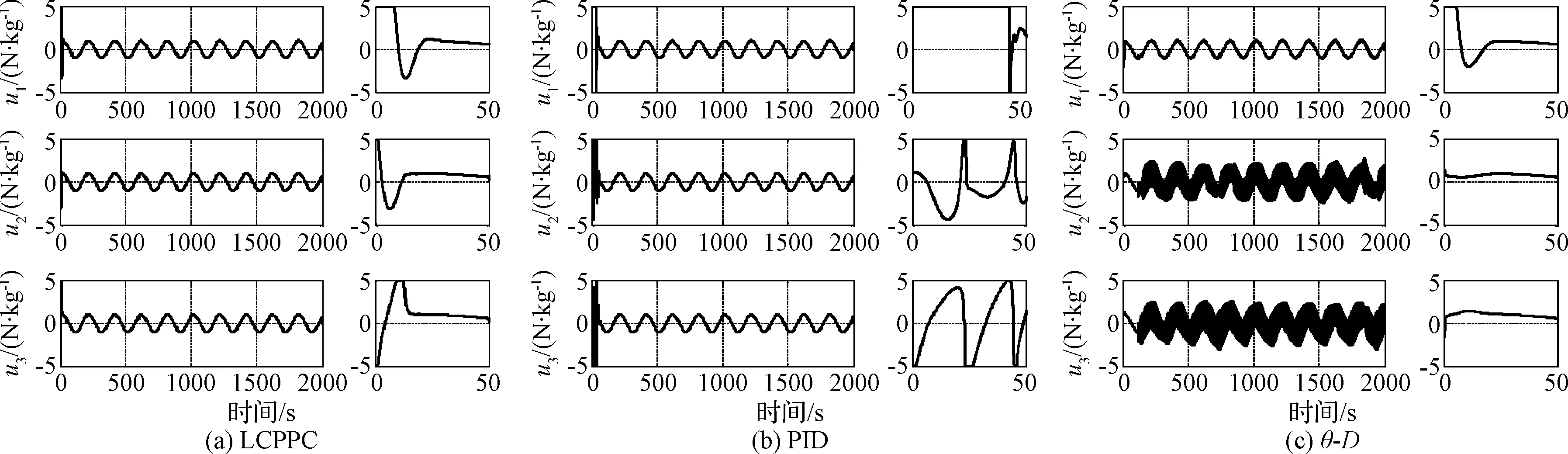
Lα(t) (9) 式中: (10) 其中,δ是为防止状态量超调而定义的常量,满足 (11) 2.2 相对轨道无模型预设性能控制 针对式(6)所示的相对轨道运动模型,定义如下广义状态量 zo(t)=xo1(t)+λoxo2(t) (12) 式中:常值矩阵λo=diag(λo1,λo2,λo3)。在定义广义状态量时,考虑相对轨道速度xo2(t)的目的是为了保证预设性能控制器在相对轨道初速度很大的情况下仍能保证系统的稳定。 结合式(9)中预设性能函数的概念,针对广义状态量zo=[zo1,zo2,zo3]T,定义如下所示的相对轨道预设性能边界 Loiαoi(t) (13) 式中:Loi,Uoi的定义方式与式(10)相同,且 此外,参数矩阵λo在进行参数选取时,应满足 0<λoiβoi<1,i=1,2,3 (14) 对定义在(Loi,Uoi)上的任意变量ξoi,定义非线性映射函数Poi:(Loi,Uoi)→R,i=1,2,3如下 Poi(ξoi)=ln[(ξoi-Loi)/(Uoi-ξoi)],i=1,2,3 (15) 该函数局部Lipschitz可微,且满足 基于式(15)中的非线性映射函数,可利用广义状态量zo(t)构造映射状态量so=[so1,so2,so3]T如下 (16) 则相对轨道无模型预设性能控制器设计为 (17) 式中:ko>0为可调增益,Ro=diag(ro1,ro2,ro3)且 Qo=diag(ηo1,ηo2,ηo3)为一正定对角阵,且其参数的选取应满足 so(zo(0))TQoso(zo(0))<1 (18) (19) 从上述控制器形式可以看出,控制量的计算过程不包含任何系统信息(均由状态反馈计算得到),是一种典型的无模型控制方法。同时,控制器计算过程也不包含任何自适应、参数辨识和寻优迭代过程,控制器复杂度很低,可以在线使用。 2.3 姿态跟踪无模型预设性能控制 针对式(7)所示的姿态跟踪运动模型,可设计如下姿态跟踪无模型预设性能控制器 在进行稳定性证明前,首先给出证明必需的一个定义与两个引理。 定义 1[17]. 考虑如下所示的初值问题 (21) 定理 1. 考虑式(6)所示的相对轨道运动控制系统和无模型预设性能控制器(19),假设相对运动干扰d、非合作目标的未知加速度a均保持有界,则系统(6)中的相对轨道状态量xo1将以预设的指数收敛速度收敛于预设稳定域内。 证. 定理1将通过以下三个步骤进行证明。第一步,证明状态量θoi(soi(zoi(t)))(后文中简记为θoi(t))在某非空开集中存在唯一最大解。 (22) 对θoi(t)求导可得 (23) 第二步,证明广义状态量zo(t)以预设的指数速度收敛于预设稳定域内。 考虑映射状态量so,在区间[0,tmax)上定义如下李雅普诺夫函数 (24) 对该函数求导可得 (25) 对式(16)进行微分运算有 (26) 将式(12)及系统状态方程(6)代入式(26)可得 (27) 式中:foi为fo的第i维元素,goij为矩阵go第i行第j列的元素。 式(27)可改写为如下矢量形式 (28) 式中: Ao(t)=diag(αo1(t),αo2(t),αo3(t)) 因此可以得到: (29) 将式(29)代入式(25)中可得 (30) (31) 则由式(30)和式(31)可得 (32) (33) (34) 式中:gmin为go的最小奇异值,λmin=min(λo1,λo2,λo3),ηmin=min(ηo1,ηo2,ηo3),rmax=max(ro1,max,ro2,max,ro3,max),roi,max为roi(t)在区间[0,tmax)上的上界。 (35) 考虑到 (36) 0≤κ(t)≤κ*=max{κ(0),γ/(γ+C)}<1 (37) 进而由κ(t)的定义可以得到 i=1,2,3, ∀t∈[0,tmax) (38) 恒成立。结合式(15)和函数Poi的单调性可以得到如下关系 (Loi,Uoi) (39) 根据引理2可得,若tmax<+∞,那么对于ζθoi的任意紧集都存在t′∈[0,tmax)使得θoi(t′)不恒在该紧集内。然而,在式(39)中寻找到ζθoi的一个紧集 (40) 使得θoi(t)恒位于该紧集内,因此可得 tmax=+∞ (41) 进而可以得出:θoi(t)在[0,+∞)上恒位于开集(Loi,Uoi)以内。换言之,广义状态量zo(t)在[0,+∞)上以预设的指数速度收敛于预设稳定域内。 第三步,证明当广义状态量zo(t)以预设的指数速度收敛于预设稳定域内时,相对轨道运动状态量xo1(t)也将以指数速度收敛于该稳定域内。 在第二步中,已经证明了广义状态量zo(t)的性质。考虑广义状态量zo(t)的定义式(12),以zo(t)作为系统(12)的输入,xo1(t)作为该系统的输出,则系统(12)可以看作一个线性时不变解耦系统。该系统的第i维(i=1,2,3)的传递函数为 (42) 式中:sl为拉普拉斯算子,w=1/λoi。传递函数的时域微分方程可由拉氏反变换得到 h(t)=L-1(H(sl))=wexp(-wt) (43) 根据式(42)和式(43),有 xo1,i(t)=zoi(t)*h(t)= ∫t0zoi(τ)h(t-τ)dτ (44) (45) 定理1证明完毕。 姿态跟踪系统(7)在无模型预设性能控制器(20)作用下的稳定性证明与上述证明过程类似,不再赘述。 为进行控制性能对比,本文将所提出的低复杂度预设性能控制(Low-complexity prescribed performance control,LCPPC)方法与两种典型的控制方法进行对比分析:第一种是无模型控制方法中的典型方法,PID控制方法;第二种是模型依赖控制方法中的典型方法,基于非线性最优控制的θ-D方法[4]。 4.1 仿真条件与参数设置 为进行对比仿真,两组仿真的初始条件设置与文献[4]相同。 在轨道初始条件方面,追踪航天器和非合作目标的初始轨道要素设置见文献[4]中的表1。初始时追踪航天器到非合作目标的距离ρ(0)设置为0.3 km,最终相对距离为ρf=0.02 km,非合作目标特征点方向为nb=[1,0,0]T,轨道控制发动机所提供的单轴最大加速度为4.9 N/kg。 4.2 非合作目标自旋但无机动 在本文仿真中,假设相对运动过程无干扰,且非合作目标只进行自旋,不存在未知机动。该工况相对理想,主要用来校验所提出控制方法的可行性。图2~6为三种控制器的仿真与对比图。 图2为LCPPC控制器作用下的相对运动轨迹示意图。从图2可以看出,追踪航天器首先快速接近非合作目标,进而悬停在非合作目标特征点上方20 m处进行观测。 图2 LCPPC作用下的相对运动轨迹Fig.2 Relative motion trajectory under LCPPC 图3为三种控制方法分别作用下的相对位置的变化图。从图3可以看出,三种方法均可以完成对非合作目标的视线跟踪。LCPPC方法能够使追踪航天器以最快的速度接近非合作目标,收敛时间约18 s。基于最优控制的θ-D方法由于良好的优化效果,呈现的性能也十分优异,收敛时间为23 s。而PID方法由于不使用模型信息,动态性能较差,收敛时间为40 s。 图4为接近与跟踪过程中视线倾角与视线偏角的变化图。从图4可以看出,LCPPC的控制方法尽管未知系统信息,但仍能使视线角以很快的速度收敛。θ-D方法的收敛也十分平稳,但收敛速度稍慢。PID控制方法作用下的系统在收敛的过程中出现了很大的震荡。 图3 非合作目标无机动时的相对距离变化图Fig.3 Relative distance without orbit maneuver of non-cooperative target 图5为仿真中相对轨道运动的控制加速度变化图。从图5可以看出,PID控制方法的控制加速度波动很大,在收敛的过程中浪费了很多的能量。LCPPC方法收敛过程很稳定,且燃料消耗较小。θ-D方法表现最为优异,仅使用很小的能量就能完成系统稳定。但是值得注意的是,相对于其他两种方法,θ-D方法使用了精确的系统模型,且耗费了较多的时间进行优化,并不适用于实际系统的在线控制。 图4 非合作目标无机动时的视线角变化图Fig.4 Angle of LOS without orbit maneuver of non-cooperative target 图5 非合作目标无机动时的控制加速度变化图Fig.5 Control accelerations without orbit maneuver of non-cooperative target 图6为仿真中真实姿态四元数矢量部分qv和期望四元数矢量部分qdv的变化图。从图6可以看出,三种控制方法在稳态过程均能使真实四元数保持较高的精度。在瞬态过程中,LCPPC方法的期望四元数相对稳定,真实四元数跟踪过程迅速。PID方法由于相对轨道控制过程的系统状态出现震荡,给出的期望四元数也出现震荡,跟踪难度加大。θ-D方法的期望四元数相对稳定,但是真实四元数的跟踪过程相对较慢。 4.3 非合作目标存在未知机动 在本文仿真中,假设非合作目标不仅存在自旋运动,还存在控制系统未知的机动行为,追踪航天器还存在质量和惯量矩阵的不确定性。该工况主要用来验证所提出控制方法在复杂条件下的性能和鲁棒性。假设非合作目标存在的未知机动和系统外部干扰的总和(以非合作目标的未知机动为主,系统外部干扰量级较小)为: 追踪航天器的质量存在30%的不确定性(即真实施加的控制加速度变为原来的1/1.3倍),追踪航天器的惯量矩阵存在不确定性ΔJ=diag(-5,3,7),仿真的其它初始条件和所有的控制参数选择均与第4.1节相同。 图7为三种控制方法分别作用下的相对位置的变化图。从图7可以看出,尽管非合作目标存在未知机动、系统存在不确定性和外部干扰,LCPPC控制方法仍能保证系统以较快的速度收敛(25 s),且在非合作目标存在未知机动时,能够保证相对位置控制精度在±0.5 m以内(若实际任务需要更高的控制精度,则可调节预设性能函数来实现)。PID控制方法作用下的系统收敛速度仍然比较慢,且出现了较大震荡,但是稳态控制精度不受非合作目标未知机动、不确定性和外部干扰的影响,保持了较高的精度。θ-D方法能够使系统较快收敛,系统进入稳态后,由于对非合作目标的机动信息和模型不确定性缺乏认知,因此优化后的控制量无法使稳态跟踪过程保持较高的精度,最终只能保证相对位置控制精度在±3 m以内。 图6 非合作目标无机动时的姿态四元数变化图Fig.6 Attitude quaternion without orbit maneuver of non-cooperative target 图8为系统稳定过程中三种方法所需的控制加速度变化图。从图8可以看出,LCPPC方法在非合作目标存在未知机动、系统存在不确定性和外部干扰的情况下,所需的控制力仍然保持较低水平。PID控制器在开始时所需的控制力较大,但是在稳态能够保持较低水平。而θ-D方法虽然在开始时能够使用的控制力很小,但是在进入稳态后,由于对非合作目标的机动信息缺乏了解,优化过程计算困难,控制加速度出现了严重的震荡,会浪费大量的燃料。 图7 非合作目标存在未知机动时的相对位置变化图Fig.7 Relative distance with unknown orbit maneuver of non-cooperative target 图8 非合作目标存在未知机动时的控制加速度变化图Fig.8 Control accelerations with unknown orbit maneuver of non-cooperative target 本文针对非合作目标的接近和视线跟踪问题,基于相对运动模型设计了相对轨道和姿态跟踪的低复杂度预设性能控制器,并证明了该控制方法能够在未知模型的前提下保证系统的瞬态和稳态性能在预设范围内。通过与两种典型的控制方法进行数值仿真对比可以得出:针对非合作目标这种存在强不确定性、强干扰和未知机动等特点的特殊对象,传统的模型依赖控制方法(如θ-D方法等)无法获得精确的系统信息,工程应用能力差;传统的无模型控制方法(如PID等)虽然具有较强的稳定性,但其控制性能很差,无法保证追踪航天器的安全和精度;本文提出的无模型预设性能控制方法不仅不需要对系统信息和不确定性进行先验了解或在线辨识,还能够保证系统状态满足实际工程预设的性能范围,具有较强的理论意义和工程应用价值。 [1] 国家自然科学基金委员会. 空间翻滚目标捕获过程中的航天器控制理论与方法[EB/OL]. 2016[2017].http://www.nsfc.gov.cn/publish/portal0/tab235/info53702.htm. [2] 梁斌, 杜晓东, 李成,等. 空间机器人非合作航天器在轨服务研究进展[J]. 机器人, 2012, 34(2):242-256. [Liang Bin, Du Xiao-dong, Li Cheng, et a1. Advances in servicing for non-cooperative spacecraft [J]. Robot, 2012, 34(2): 242-256.] [3] 陈统, 徐世杰. 非合作式自主交会对接的终端接近模糊控制[J]. 宇航学报, 2006, 27(3):416-421. [Chen Tong, Xu Shi-jie. A fuzzy controller for terminal approach of autonomous rendezvous and docking with non-cooperative target [J]. Journal of Astronautics, 2006, 27(3): 416-421.] [4] 高登巍, 罗建军, 马卫华,等. 接近和跟踪非合作机动目标的非线性最优控制[J]. 宇航学报, 2013, 34(6): 773-781. [Gao Deng-wei, Luo Jian-jun, Ma Wei-hua, et al. Nonlinear optimal control of spacecraft approaching and tracking a non-cooperative maneuvering object [J]. Journal of Astronautics, 2013, 34(6): 773-781.] [5] 姜博严, 胡庆雷, 石忠,等. 与自由翻滚目标近距离段交会对接的相对姿轨耦合控制[J]. 宇航学报, 2014, 35(1):54-60. [Jiang Bo-yan, Hu Qing-lei, Shi Zhong, et al. Relative position and attitude coupled controller design for approaching and docking with a freely tumbling target [J]. Journal of Astronautics, 2014, 35(1): 54-60.] [6] Weiss A, Baldwin M, Erwin R S, et al. Model predictive control for spacecraft rendezvous and docking: strategies for handling constraints and case studies [J]. IEEE Transactions on Control Systems Technology, 2015, 23(4): 1638-1647. [7] 郭永, 宋申民, 李学辉. 非合作交会对接的姿态和轨道耦合控制[J]. 控制理论与应用, 2016, 33(5):638-644. [Guo Yong, Song Shen-min, Li Xue-hui. Attitude and orbit coupled control for non-cooperative rendezvous and docking [J]. Control Theory & Applications, 2016, 33(5): 638-644.] [8] 冯丽程, 白玉铸, 陈小前. 航天器避障交会有限时间滑模控制[J]. 宇航学报, 2016, 37(11): 1342-1348. [Feng Li-cheng, Bai Yu-zhu, Chen Xiao-qian. Finite-time sliding mode control for spacecraft rendezvous with collision avoidance [J]. Journal of Astronautics, 2016, 37(11): 1342-1348.] [9] 朱战霞, 马家瑨, 樊瑞山. 基于螺旋理论描述的空间相对运动姿轨同步控制[J]. 航空学报, 2016, 37(9):2788-2798. [Zhu Zhan-xia, Ma Jia-jin, Fan Rui-shan. Synchronization control of relative motion for spacecraft with screw theory-based description [J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(9): 2788-2798.] [10] Bechlioulis C P, Rovithakis G A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance [J]. IEEE Transactions on Automatic Control, 2008, 53(9): 2090-2099. [11] Bechlioulis C P, Rovithakis G A. A low-complexity global approximation-free control scheme with prescribed performance for unknown pure feedback systems [J]. Automatica, 2014, 50(4): 1217-1226. [12] Theodorakopoulos A, Rovithakis G A. Low-complexity prescribed performance control of uncertain MIMO feedback linearizable systems [J]. IEEE Transactions on Automatic Control, 2016, 61(7): 1946-1952. [13] Karayiannidis Y, Papageorgiou D, Doulgeri Z. A model-free controller for guaranteed prescribed performance tracking of both robot joint positions and velocities[J]. IEEE Robotics & Automation Letters,2016, 1(1): 267-272. [14] Bu X, Wu X, Huang J, et al. Robust estimation-free prescribed performance back-stepping control of air-breathing hypersonic vehicles without affine models[J]. International Journal of Control, 2016, 89(11): 2185-2200. [15] Wei C, Luo J, Dai H, et al. Efficient adaptive constrained control with time-varying predefined performance for a hypersonic flight vehicle [J]. International Journal of Advanced Robotic Systems, 2017, 14(2): 1-17. [16] Shuster M D. A survey of attitude representation [J]. Journal of the Astronautical Sciences, 1993, 41(4): 439-517. [17] Sontag E D. Mathematical control theory: deterministic finite dimensional systems[M]. New York:Springer, 1998. 通信地址:陕西省西安市友谊西路127号(710072) 电话:18192281473 E-mail: yinzy0126@foxmail.com Low-Complexity Prescribed Performance Control for Approaching andTracking a Non-Cooperative Target YIN Ze-yang1,2, LUO Jian-jun1,2, WEI Cai-sheng1,2, YUAN Jian-ping1,2 (1. School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China;2. Science and Technology on Aerospace Flight Dynamics Laboratory, Xi’an 710072, China) A low-complexity prescribed performance control (LCPPC) method on basis of the prescribed performance control theory is proposed in this paper for a chasing spacecraft approaching and tracking a non-cooperative target spacecraft. Any information of the system parameters, including the mass and inertia matrix of the chasing and target spacecraft, is unnecessary. Moreover, the transient performance as well as the steady performance of the system can be prescribed and guaranteed despite the external disturbance, parameter uncertainties and unknown non-cooperative target’s maneuver. The simulation results show that the high precision real-time control is realized for approaching and tracking the non-cooperative target in a line-of-sight coordinate system. Prescribed performance control; Non-cooperative target; Model-free; Low-complexity; Robust control 2017- 04- 05; 2017- 05-22 国家自然科学基金(61690211,11472213);西北工业大学博士论文创新基金(CX201711) V448 A 1000-1328(2017)08-0855-10 10.3873/j.issn.1000-1328.2017.08.010 殷泽阳(1993-),男,博士生,主要从事航天飞行动力学与控制方面研究。
3 稳定性分析
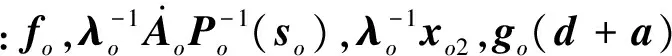
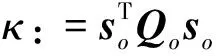
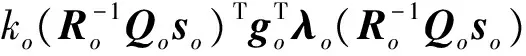
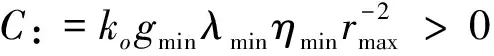
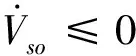
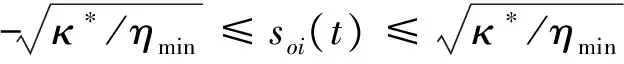
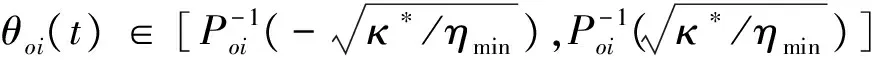
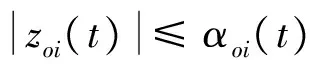

4 仿真校验
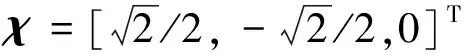
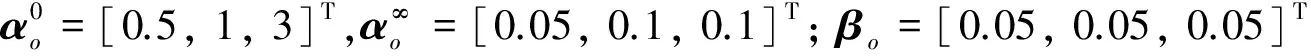
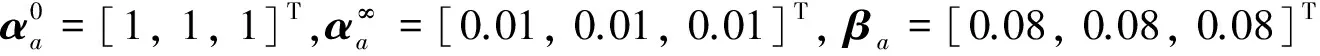
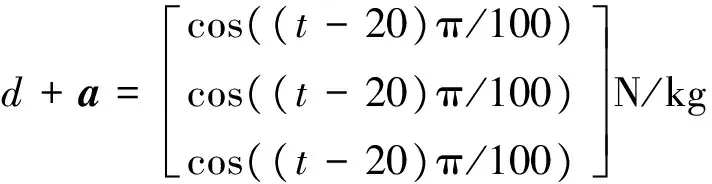
5 结 论
