再入等离子体流动及其电磁波传输效应研究

高铁锁，董维中，江 涛，丁明松，刘庆宗

(中国空气动力研究与发展中心计算空气动力研究所，绵阳 621000)

再入等离子体流动及其电磁波传输效应研究

高铁锁，董维中，江 涛，丁明松，刘庆宗

(中国空气动力研究与发展中心计算空气动力研究所，绵阳 621000)

基于求解N-S方程的数值方法和求解波动方程的WKB方法，建立了高超声速再入等离子体流场及其对电磁波传输影响的计算分析手段。通过比较分析飞行条件下再入体周围等离子体分布及其对通信的影响，初步验证了计算分析方法的可行性。在对再入等离子体流场数值模拟的基础上，计算了不同频率电磁波在等离子体介质中的传输特性，分析了再入体壁面催化条件及等离子体碰撞频率等因素对不同频率电磁波传输特性的影响。研究表明：再入高度越高，壁面催化对等离子体分布及其电磁波传输的影响越大；当电磁波频率低于特征碰撞频率时，碰撞频率可对电磁波传输特性产生显著影响。

等离子体；电磁波传输；壁面催化；电子数密度；碰撞频率；再入

0 引 言

高超声速飞行器技术的发展及未来深空探测任务对测控通信提出了严峻挑战[1-3]。高超声速飞行器在再入地球大气层或进入火星等星球大气环境过程中，与大气相互作用，在飞行器的周围形成脱体激波和粘性附面层。由于激波与粘性的作用，波后气体产生离解、电离、壁面材料的催化、热解与烧蚀等高温效应，在飞行器周围形成非均匀等离子体鞘套。电磁波信号在等离子体鞘套中传播过程中，产生吸收、反射和折射等传输效应，导致传播信号发生衰减，严重时造成飞行器与外界(地面或中继卫星等)的通信中断，对飞行器的实时控制与飞行安全构成威胁。高超声速飞行器周围等离子体分布与飞行器外形尺寸、飞行弹道、姿态及壁面材料等因素有关，而电磁波在等离子体中的传输特性则受通信天线附近等离子体分布和电磁波频率及入射方向等因素影响。因此，在进行高超声速飞行器总体设计时，需要综合考虑这些因素，对飞行器周围等离子体鞘套对通信的影响进行计算分析和评估，在此基础上提出消除或减缓等离子体对通信影响的手段和方法[3-5]，以满足高超声速飞行器通信及测控系统的设计需求。

在无外加磁场情况下，高超声速飞行器周围等离子体鞘套可看作各向同性等离子体，此时可采用基于CFD的数值方法对飞行器等离子体鞘套进行模拟，获得计算电磁波传输效应所需的等离子体参数，有关等离子体数值模拟的可靠性及影响分析可参见文献[6-8]。预测等离子体电磁波传输效应的方法主要有两类，一类是基于直接求解Maxwell方程的数值方法，比较典型的有时域有限差分方法[9-10]，另一类是基于求解波动方程的近似方法如WKB方法等[11-12]。WKB方法适用于电磁参数缓变的等离子体介质，实际应用于非均匀等离子体层时引入分层介质概念。时域有限差分数值方法模拟精度高，但计算量相对较大，而WKB方法的计算精度虽不如数值方法，但计算量相对较小，适合分析再入过程中等离子体鞘套对电磁波信号的影响特征和规律。

等离子体电磁波传输效应涉及高温气体动力学、化学动力学与电磁学等学科的交叉和融合，在数值模拟和分析方面还面临诸多难题和挑战[4,13-14]。对于再入等离子体流动的数值模拟，还受到再入体壁面催化条件和化学动力学模型等重要因素的影响[6-7]，而再入等离子体流动的数值模拟结果将直接影响电磁波传输效应的预测结果。目前国内外在计算分析再入体周围等离子体鞘套的电磁波传输效应时，通常认为再入体表面组分满足某一种催化条件[9-12]，即满足完全催化壁(Fully catalytic wall,FCW)或完全非催化壁(Non catalytic wall,NCW)条件，而且在有些计算分析中还忽略了等离子体碰撞频率的影响[2,11]。另外，在已有研究工作中，有关数值研究工作主要聚焦在再入等离子体流场或其传输特性某一方面，针对再入等离子体流场及其传输效应的综合分析工作较少。本文针对RAM C-II再入弹道条件[15-16]，基于自主研发的非平衡等离子体流场及其电磁波传输效应计算工具，比较分析两种典型催化条件及等离子体碰撞频率对再入等离子体分布和电磁波传输效应的影响特征和规律。

1 再入等离子体流动数值模拟方法

数值模拟等离子体流动的控制方程为三维化学非平衡N-S方程，其无量纲化形式如下：

(1)

式中:守恒变量Q=[ρi,ρ,ρu,ρv,ρw,ρE]T，化学非平衡源项W=[wi,0,0,0,0,0]T，ρi是组分i的密度，u,v,w对应直角坐标系下三个方向的速度，E为总能，Re为雷诺数，F,G,H与FV,GV,HV分别对应三个不同方向的无黏与黏性通量，W为化学反应非平衡源项，wi是组分i的化学反应净生成率。

表1 Park模型

2 再入等离子体中电磁波传输效应的计算方法

当电磁波在非磁化等离子体中传播时，由Maxwell方程组可推导出波动方程：

(2)

其中,E为电场强度，k为波数。考虑一维情况，认为等离子体参数仅在z轴方向非均匀变化，且平面电磁波沿z轴正向传播，此时电场只随z轴发生变化。设电场平行于y轴，对于缓变非均匀等离子体介质，方程(2)的WKB解[20]：

(3)

设能量为P0的电磁波从z=0处垂直入射到等离子体内部并在z=d界面处透射出来，电磁波在此处的能量P为：

(4)

电磁波通过等离子体的衰减可以表示为：

(5)

等离子体中电磁波的复波数k的表达式：

k=β-jα

(6)

其中，α与β分别为衰减系数与相位常数，具体表达式为：

(7)

(8)

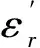
(9)

其中，ω与ωp分别表示电磁波与等离子体的角频率，空气等离子体的碰撞频率ν用含温度和压力的工程关系式进行计算[4]。

3 计算结果与分析

RAM C-II典型再入弹道如图1所示[3,15]，其中给出再入速度随高度的变化特征及VHF信号的中断情况。天线位置在x=6.4Rn处，认为电磁波沿物面法向传播。RAM C-II再入体外形为钝锥体，其头部半径Rn= 0.1524 m，半锥角9°，长度1.295 m，飞行攻角为0°，壁面温度取1500 K，球头壁面材料为金属铍，再入中没有烧蚀发生[16]。壁面催化条件为完全催化壁(FCW)或完全非催化壁(NCW)，它们对应的壁面组分质量分数分别满足ci=ci∞或∂ci/∂n=0，即满足来流条件或壁面法向梯度为零的条件。

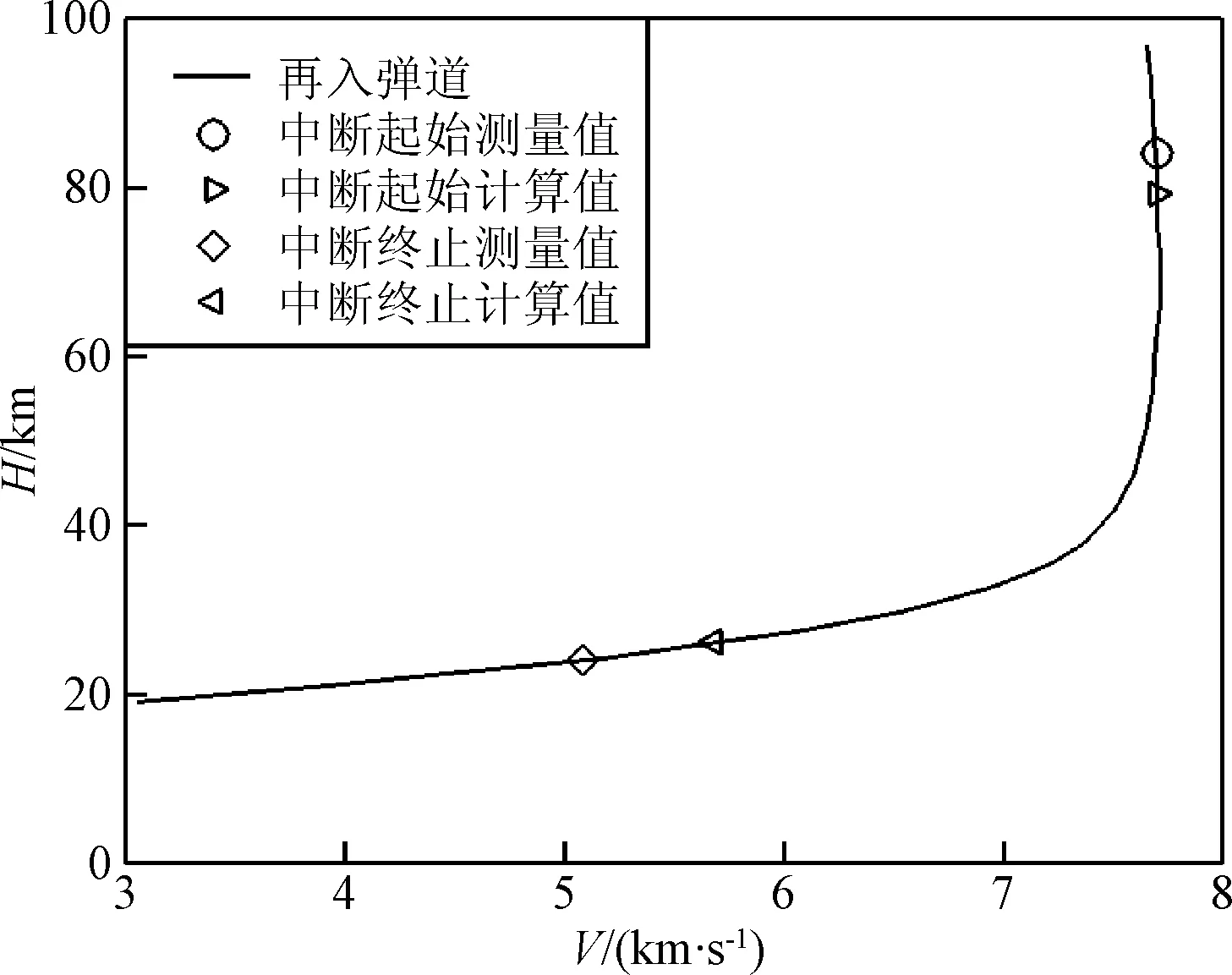
图1 RAM C-II再入飞行弹道与通信中断区间 Fig.1 RAM C-II reentry trajectory showing onset and end of signal blackout

3.1 壁面催化对再入等离子体分布及电磁波传输效应的影响

本节重点分析RAM C-II再入等离子体对VHF频段(f=0.26 GHz)电磁波传输特性的影响，并与飞行测量数据进行对比。基于RAM C-II 再入弹道，对再入体等离子体绕流进行数值模拟，图2给出高度71 km再入体周围等离子体绕流温度与电子数密度的分布情况，可见随着等离子体流动从再入体头部向下游发展，流场温度总体上随之降低，电子数密度逐渐衰减，等离子体厚度逐渐增大。比较对称轴上、下的完全催化壁(FCW)与完全非催化壁(NCW)的模拟结果可以看出，壁面催化条件对流场温度分布影响相对较小，但对流场电子数密度分布产生了明显影响。

图3给出高度71 km不同壁面催化条件下电子数密度沿轴向和沿壁面法向的分布情况，图中横坐标x与R分别表示离开再入体头部顶点的轴向距离和离开壁面的法向距离。可见完全催化壁条件下峰值电子数密度计算与飞行测量值吻合，而x=8.1Rn处法向剖面电子数密度测量值基本处在完全催化与非催化壁的计算值之间。总体上看，完全催化壁的电子数密度计算值更接近飞行测量值[16]，因此这里主要针对完全催化壁条件，分析电磁波衰减对通信的影响并与测量进行对比。

图4给出VHF频段电磁波在等离子体中衰减沿高度变化。一般认为电磁波衰减30 dB以上时发生通信中断[21]，这样可以从图4获得通信中断的起始和终止高度的预测值，如图中完全催化壁计算曲线上的S与E点，对应通信中断的起始和终止高度分别为79 km和26 km，而实际飞行测量的通信中断起始与终止高度分别在84 km与24 km附近[3,15]，如图1所示。如果以图4中完全非催化壁条件下的电磁波衰减进行估算，通信中断的起始和终止高度大约在85 km与26 km附近。可见，通信中断预测值与飞行测量值比较一致，也符合催化条件对再入等离子体中电磁波衰减的影响规律。

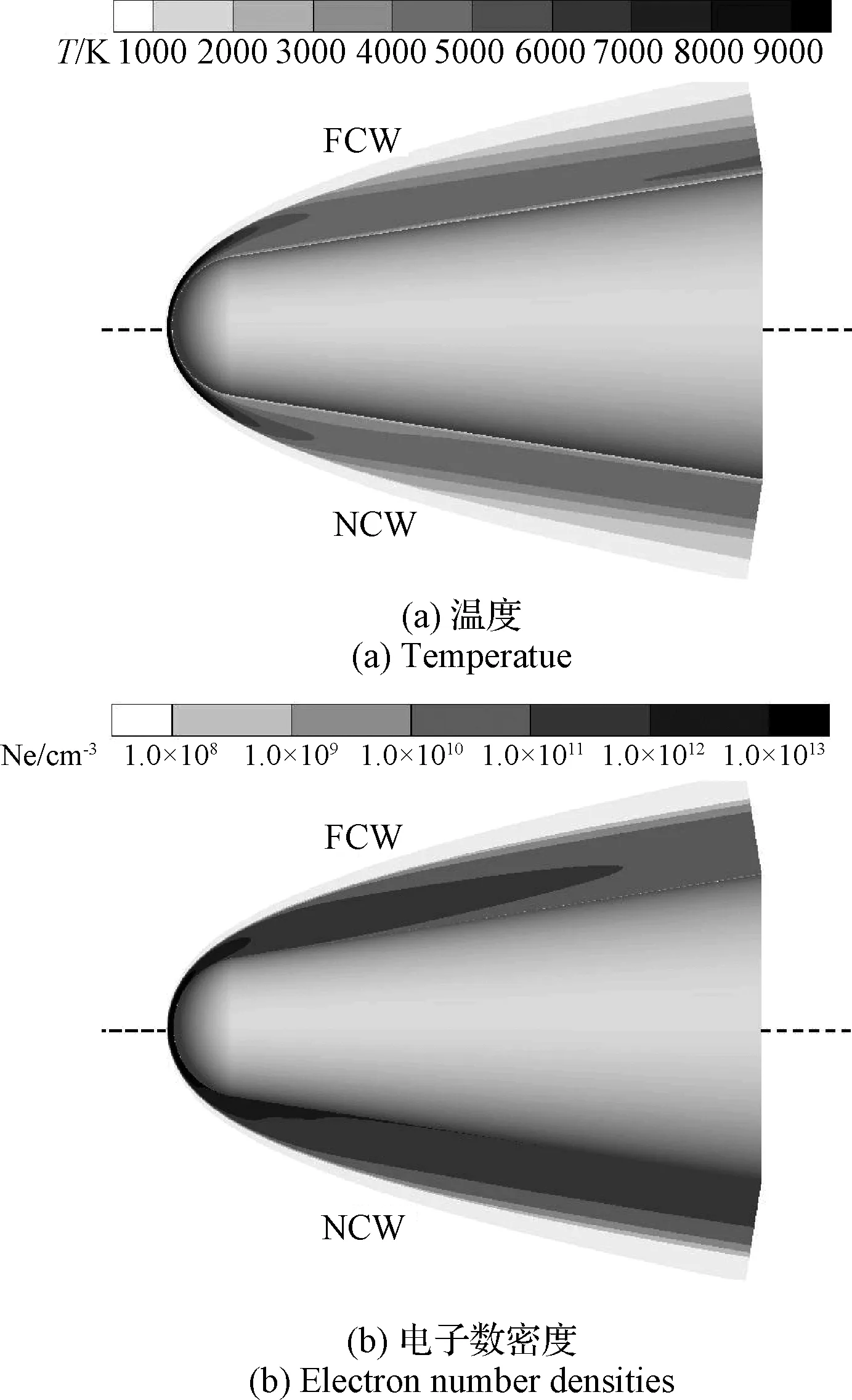
图2 再入体绕流等离子体参数分布Fig.2 Distribution of plasma parameters

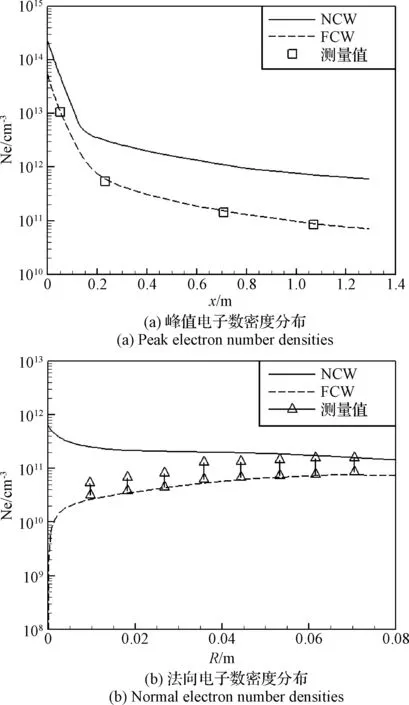
图3 计算与测量结果比较Fig.3 Computational and experimental data

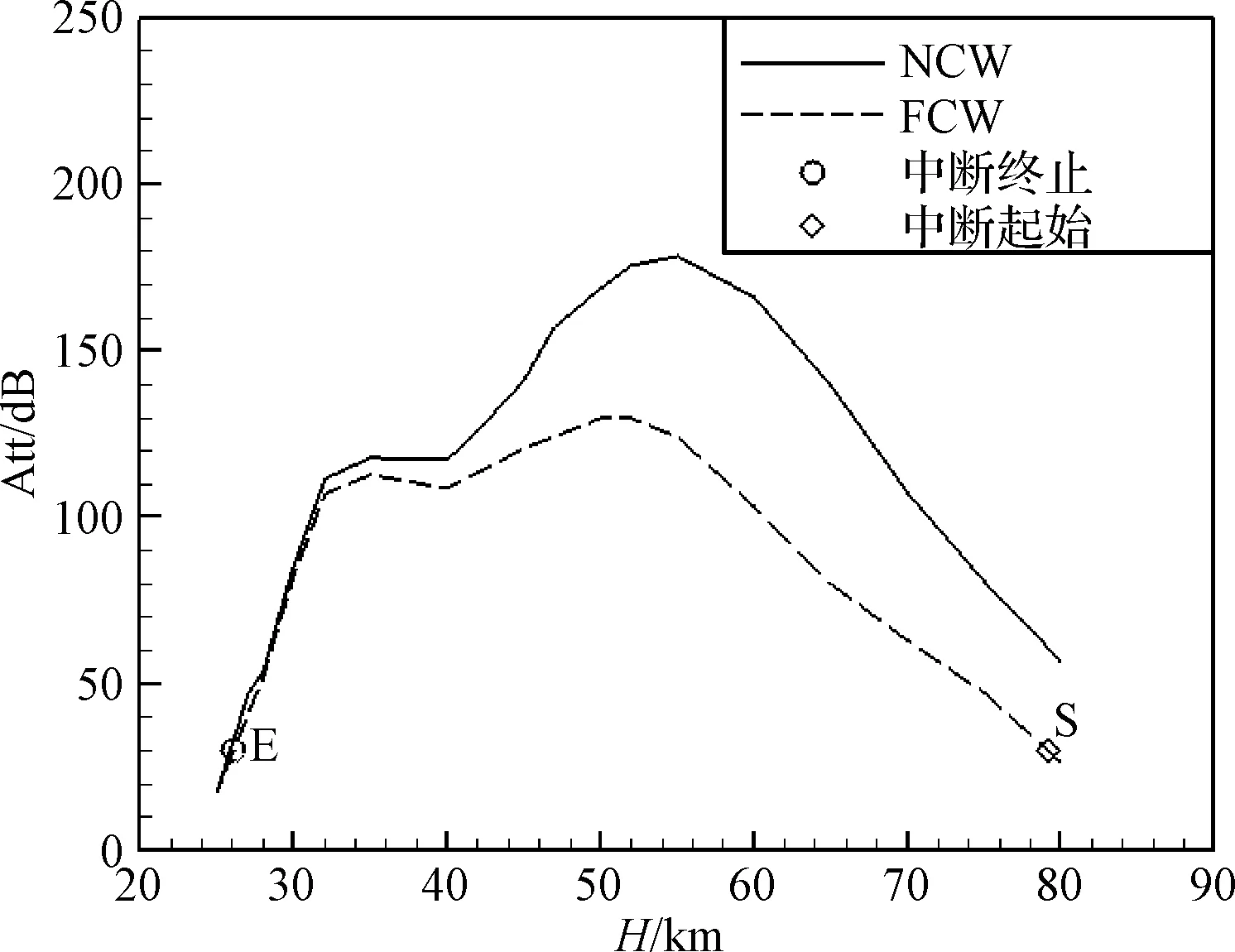
图4 再入等离子体对电磁波传输及通信的影响Fig.4 Effects of plasma on eletromagnetic wave transmission and communication

从图4还可以看出，在高空区域，非催化壁条件下电磁波衰减的计算值明显高于完全催化条件的计算值，在54 km左右二者的差异达到最大，之后随着再入高度降低二者的差异逐渐减小。不同壁面催化条件对电磁波衰减的影响特征主要和不同催化条件导致的等离子体分布的变化特征有关。

从高空再入地球大气层过程中，再入体绕流经历热化学非平衡到平衡的变化过程。在70 km高空条件下非平衡效应较强，不同催化条件导致的再入等离子体分布差异较为明显，对电子数密度分布的影响区域也较大，而在30 km低空条件下非平衡效应较弱，催化条件对电子数密度的影响区域相对较小，只在壁面附近产生影响，如图5(a)所示。这里采用关于温度和压力的工程估算式对碰撞频率进行估算[4]，而壁面催化对流场压力影响很小，对流场温度有一定影响，但总体上影响不大(见图2)，这使得不同壁面催化条件对等离子体碰撞频率的影响不大，如图5(b)所示。

从式(5)～(9)可知，对特定频率电磁波衰减起作用的等离子体参数主要是电子数密度和碰撞频率，从对图5的分析可知，壁面催化条件对电子数密度分布影响明显，对碰撞频率分布影响较小，表明导致不同催化条件下电磁波衰减差异的根本原因在于不同壁面催化引起的天线附近等离子体流动中电子数密度分布的变化。

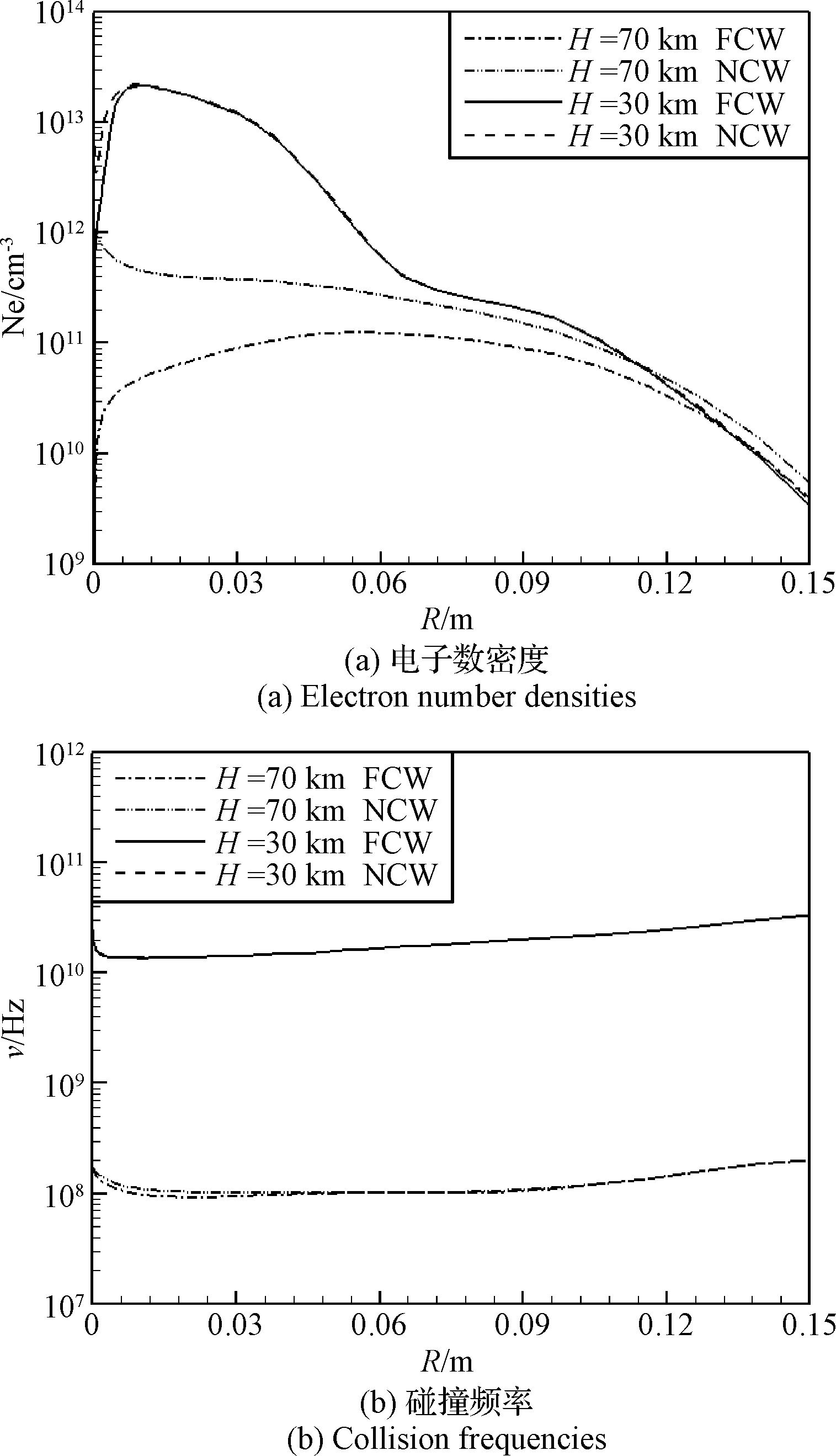
图5 壁面催化对等离子体参数的影响Fig.5 Effects of surface catalysis on plasma parameters

3.2 等离子体碰撞频率对不同频率电磁波传输效应的影响

以RAM C-II再入条件作为研究对象，针对完全催化壁条件(完全非催化壁的情况类似)进行分析。从图6可以看出,再入体头部驻点附近特征电子数密度随高度的变化特征，即在30 km左右特征电子数密度出现峰值。这里特征电子数密度取头部驻点附近区域的最大值。从80 km到30 km再入过程中，再入体速度大约从7.7 km/s降至6.5 km/s(见图1)，速度变化相对平缓，驻点附近特征电子数密度受大气密度的影响更大，使得特征电子数密度随高度的降低而增加。对于钝锥体轴对称再入体，其锥身部壁面法向峰值电子数密度满足特征关系[3]：

(10)

式中:m、n为常数，可见沿物面某轴向位置处的法向峰值电子数密度随驻点附近特征电子数密度及来流大气密度的增加而增大。从图7(a)可见，由于特征电子数密度与大气密度均随高度的降低而增大，导致天线位置x=6.4Rn处峰值电子数密度随高度的降低而增大。从图7(b)可见，在离开壁面激波层内的大部分区域，碰撞频率变化较为平缓，从70 km到30 km再入过程中碰撞频率随着高度降低而增大。

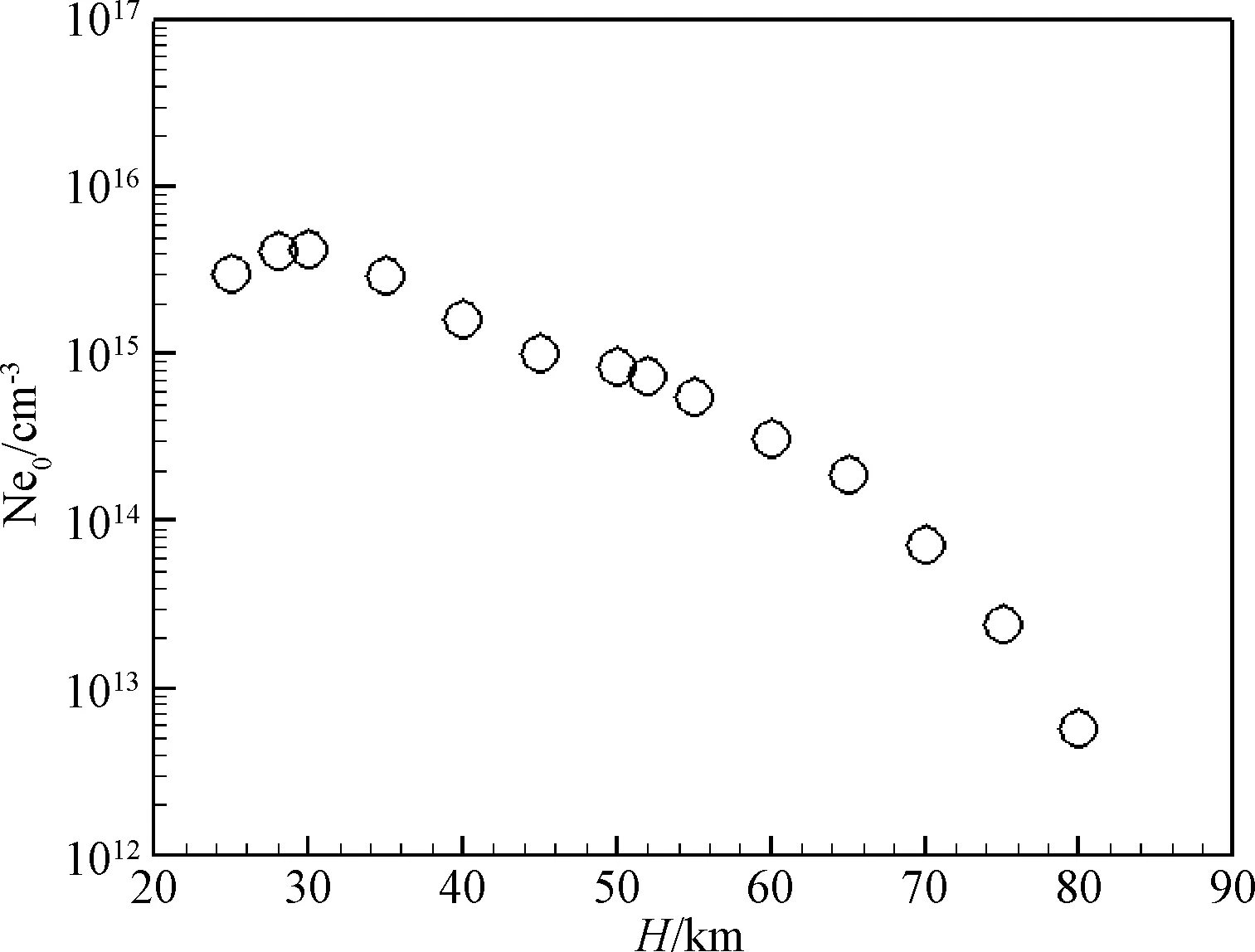
图6 驻点附近特征电子数密度随高度变化Fig.6 Characteristic electron number densities near stagnation point at different heights

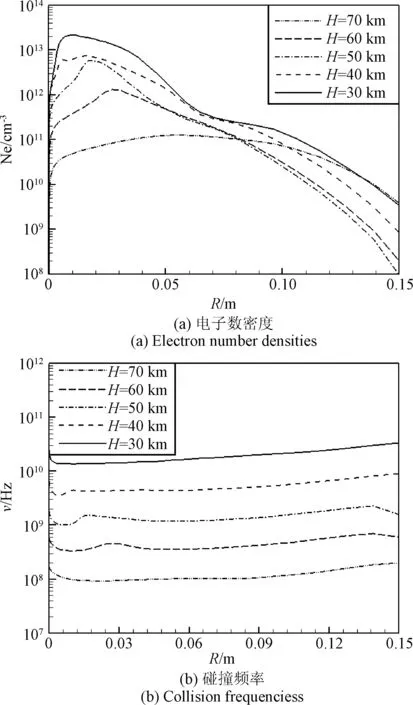
图7 等离子体参数沿壁面法向分布(x=6.4Rn)Fig.7 Distribution of plasma parameters in surface normal direction(x=6.4Rn)

图8给出不同高度下等离子体引起的电磁波衰减随电磁波频率的变化情况。从图8可见，对于碰撞频率ν≠0的实际再入情况，在70 km以下，电磁波衰减随电磁波频率变化出现峰值，此峰值对应的电磁波频率接近等离子剖面的特征碰撞频率(特征碰撞频率取剖面内碰撞频率的平均值)，这与文献[22-23]中关于均匀等离子体中电磁波衰减特征的分析结果一致。从图8还可以看出，电磁波频率越高，碰撞频率对电磁波衰减影响的程度越小，特定频率电磁波衰减值随高度的降低而增大，与峰值电子数密度随高度的变化规律一致(见图7)。

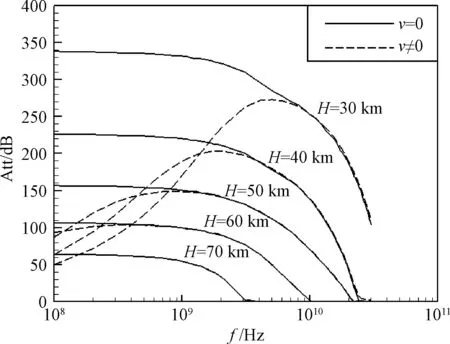
图8 等离子体碰撞频率对电磁波传输的影响(x=6.4Rn) Fig.8 Effects of collision frequencies on electromaganetic wave transmission in plasma(x=6.4Rn)

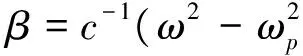
4 结 论

以RAM C-II再入飞行验条件为主要研究对象，对再入体周围等离子体分布及其电磁波传输效应进行了数值模拟与分析，得出如下基本结论：

1)在RAM C-II典型再入飞行弹道条件下，再入等离子体中电子数密度分布及其对通信影响的数值计算与飞行测量结果比较一致，初步验证了再入等离子体绕流数值模拟方法及电磁波传输效应预测方法的可行性。

2)在再入高度较高的情况下，再入体等离子体绕流处于热化学非平衡状态，壁面催化条件对再入体等离子体绕流中电子数密度分布及电磁波衰减的影响较大；在再入高度较低的情况下，再入体等离子体绕流接近热化学平衡状态，壁面催化条件对再入等离子体分布及电磁波衰减的影响相对较小。

3)在不同再入高度条件下，等离子体碰撞频率对特定频率电磁波衰减的影响程度不同；在同一再入高度条件下，碰撞频率对不同频率电磁波衰减的影响程度也不同。等离子体碰撞频率对电磁波衰减特性的影响程度主要取决于电磁波频率与特征碰撞频率的相对大小。碰撞频率对电磁波衰减的影响能否忽略，需要针对具体情况进行具体分析。

[1] 崔平远，窦强，高艾. 火星大气进入段通信“黑障”问题研究综述[J]. 宇航学报，2014，35(1)：1-12. [Cui Ping-yuan，Dou Qiang，Gao Ai. Review of communication blackout problems encountered during Mars entry phase[J]. Journal of Astronautics，2014，35(1)：1-12.]

[2] Kim M. Electromagnetic manipulation of plasma layer for reentry blackout mitigation[D]. Michigan: University of Michigan. 2009.

[3] Hartunian R A，Stewart G E，Fergason S D，et al. Causes and mitigation of radio frequency(RF) blackout during reentry of reusable launch vehicles[R]．El Segundo: The Aerospace Corporation，ATR-2007(5309)-1，2007.

[4] 张志成. 气动物理学[M]. 北京：国防工业出版社，2013：44-86.

[5] 李伟，邱景辉，索莹，等. 降低电磁波在再入等离子体中衰减的仿真分析[J]. 宇航学报，2010，31(3): 825-829. [Li Wei，Qiu Jing-hui，Suo Ying，et al. Simulation analysis of reducing electromagnetic wave attenuation through reentry plasma[J]. Journal of Astronautics, 2010，31(3): 825-829.]

[6] 高铁锁，董维中, 江涛，等. 化学模型对数值模拟等离子体流动的影响研究[J]. 宇航学报，2016，37(10): 1193-1199. [Gao Tie-suo，Dong Wei-zhong，Jiang Tao, et al. Research on effects of chemical models on numerical simulation of plasma flow[J]. Journal of Astronautics，2016，37(10): 1193-1199.]

[7] Scalabrin L C, Boyd I D. Numerical simulation of weakly ionized hypersonic flow for reentry configurations[R]. AIAA 2006-3773.

[8] Gupta R N，Yos J M，Thompson R A，et al. A review of reaction rates and thermodynamic and transport properties for an 11-species air model for chemical and thermal nonequilibrium calculations to 30000K[R]. NASA-RP-1232，1990.

[9] Takahashi Y，Yamada K，Abe T. Radio frequency blackout possibility for an inflatable reentry vehicle[R]. AIAA-2012-3110.

[10] White M D，Sherer S E. High-order simulation of communication through weakly ionized plasma for re-entry vehicles[R]. AIAA-2006-1173.

[11] Morabito D D，Kornfeld R P，Bruvold K N，et al. The Mars Phoenix communications brownout during entry into the martian atmosphere[R]. IPN Progress Report 42-179，2009.

[12] 李江挺，郭立新，方全杰，等. 高超声速飞行器等离子体鞘套中的电磁波传播[J].系统工程与电子技术，2011，33(5)：969-973. [Li Jiang-ting，Guo Li-xin，Fang Quan-jie，et al. Electromagnetic wave propagation in plasma sheath of hypersonic vehicles[J]. Systems Engineering and Electronics，2011，33(5)：969-973.]

[13] Anderson J D. Hypersonic and high-temperature gas dynamics[M]. Second edition. Virginia，2006.

[14] 叶友达. 高超声速空气动力学研究进展与趋势[J]. 科学通报，2015，60(12)：1095-1103. [Ye You-da. Advances and prospects in hypersonic aerodynamics[J]. Chinese Science Bulletin，2015，60(12)：1095-1103.]

[15] Grantham W L. Reentry plasma measurements using a four-frequency reflectometer[R]. NASA SP-252，1970.

[16] Candler G V, MacCormack R W. The computation of hypersonic ionized flows in chemical and thermal nonequilibium[R]. AIAA-88-0511.

[17] 董维中. 热化学非平衡效应对高超声速流动影响的数值计算与分析[D]. 北京：北京航空航天大学，1996. [Dong Wei-zhong. Numerical simulation and analysis of thermo-chemical non-equilibrium effects at hypersonic flows[D]. Beijing：Beijing University of Aeronautics and Astronautics，1996.]

[18] 高铁锁，李椿萱，董维中，等. 高超声速电离绕流的数值模拟[J]. 空气动力学学报，2002，20(2)：184-191. [Gao Tie-suo，Li Chun-xuan，Dong Wei-zhong，et al. Numerical simulation of hypersonic ionized flows[J]. Acta Aerodynamica Sinica，2002，20(2)：184-191.]

[19] Park C. Review of chemical-kinetic problems of future NASA missions, I: Earth entries[J]. Journal of Thermophysics and Heat Transfer，1993 7(3)：385-398.

[20] 袁敬闳，莫怀德. 等离子体中的波[M]. 成都: 电子科技大学出版社，1990：168-184.

[21] 郑灵.飞行器等离子体鞘套对电磁波传输特性的影响研究[D]. 成都：电子科技大学，2013. [Zheng Ling. Study of electromagnetic wave propagation in spacecraft plasma sheath[D]. Chengdu： University of Electronic Science and Technology of China，2013.]

[22] 袁忠才，时家明. 非磁化等离子体中的电子碰撞频率[J]. 核聚变与等离子体物理，2004，24(2)：157-160. [Yuan Zhong-cai，Shi Jia-ming. Electron collision frequency of the non-magnetized plasma[J]. Nuclear Fusion and Plasma Physics，2004，24(2)：157-160.]

[23] 于哲峰，马平，张志成，等. 微波在薄层等离子体中传输效应研究[J]. 实验流体力学，2013，27(3)：60-64. [Yu Zhe-feng，Ma Ping，Zhang Zhi-cheng，et al. Research on microwave transmission in thin layer plasma[J]. Journal of Experiments in Fluid Mechanics，2013，27(3)：60-64.]

通信地址: 四川省绵阳市涪城区二环路南段6号13信箱9分箱(621000)

电话: (0816)2463297

E-mail: gaots19654@163.com

Research on Reentry Plasma Flow and Its Effects on ElectromagneticWave Transmission

GAO Tie-suo, DONG Wei-zhong, JIANG Tao, DING Ming-song, LIU Qing-zong

(Computational Aerodynamics Institute, China Aerodynamics Research and Development Center,Mianyang 621000, China)

Based on the numerical method for solving Navier-Stokes equations and the Wentzel-Kramers-Brillouin(WKB) method for solving wave equations, the computational codes for simulating the reentry plasma flow and its effects on the electromagnetic wave transmission are developed. The methods are validated preliminarily by comparing the computational results with the experimental ones for flight conditions. On the basis of the numerical simulation of the plasma flow field，the transmission characteristics of the electromagnetic wave in plasma flow are computed, and the effects of the surface catalysis and the plasma collision frequencies on the electromagnetic wave transmission are analyzed. The research shows that the effects of the surface catalysis are more important with reentry height increasing, and the collision frequencies can influence severely the transmission of the electromagnetic wave when its frequencies are lower than the characteristic collision frequencies of plasma.

Plasma; Electromagnetic wave transmission; Surface catalysis; Electron number densities; Collision frequencies; Reentry

2016-08-08;

2017-05-25

V411.4

A

1000-1328(2017)08-0879-07

10.3873/j.issn.1000-1328.2017.08.013

高铁锁(1965-)，男，研究员，主要从事气动物理学及高温气体动力学研究。