由局域电场调控的量子演化极限

吴文炯，严 凯，谢燕青，郝 翔

（苏州科技大学 数理学院，江苏 苏州 215009）

由局域电场调控的量子演化极限

吴文炯，严 凯，谢燕青，郝 翔*

（苏州科技大学 数理学院，江苏 苏州 215009）

当两能级原子弱耦合至零温单体腔时，施加一个局域电场来有效调控量子态演化速度极限。通过无时间卷积量子主方程，推导了开放系统的退相干过程。量子演化极限与外加电场的频率和强度息息相关。从激发态占有数的观点出发，解释了量子演化极限。

退相干；量子演化极限；局域电场

在量子物理领域中，如量子通信[1]、量子计算[2]、最优控制理论[3]，一个最基本的研究内容就是要探究一个量子系统的演化规律。为了有效衡量量子演化速度，人们基于量子力学基本原理“测不准关系”，提出了量子演化极限时间QSLT[4-14]。对于一个封闭的系统，即不考虑环境对其退相干影响，量子态的演化是一种么正行为。目前，已有两种不同形式的 QSLT：Mandelstam-Tamm（MT）和 Margolus-Levitin[15]（ML），综合写成 QSLT=max{πħ/（2ΔE），πħ/（2E）}。 前者取决于初始态的能量方差，后者取决于初始态的能量平均值。 衡量量子演化时间的主要依据在于如何有效区分量子态。目前，在国际和国内的主流研究中，人们常常采用以下几种量子态区分度，如量子态保真度[16]fidelity（relative purity）、量子态保真度的形式夹角[17]Bures angle和量子费舍尔信息[18]Fisher information。这些方法表明QSLT与实际驱动时间τD密不可分。当τQSL=τD时，量子演化没有潜力加速；然而若τQSL＜τD，则表明可以促进量子演化[19]。最近，人们发现可以通过加强系统与环境相互作用[16-17]或者选取一些特殊量子态[19-20]作为初态来获得量子系统的最大演化速度。

电场作为一种有效调控手段在现实中着很多应用。如果系统与环境处在弱耦合时，就没有记忆效应，也就没有量子演化加速现象。但是可以外加一个局域电场来加速量子演化。笔者将讨论一个两能级系统和绝对零度的单体腔弱耦合并受电场驱动的模型，由此分析外加电场对量子演化极限的影响。

1 模型

模型如图1所示。

爱因斯坦理论合理假设原子对光子的发射和吸收，认为原子能级是分立的，将光场与原子的相互作用行为概括为三种基本类型：自发辐射、吸收以及受激辐射。图1描述了一个两能级系统（atom）受到光场（reservoir）的影响，原子从激发态能级与基态能级之间发生跃迁，发射或者吸收频率为ω0的光子。对单粒子与环境耦合模型施加一个电场，那么系统与环境的总哈密顿量可表示为

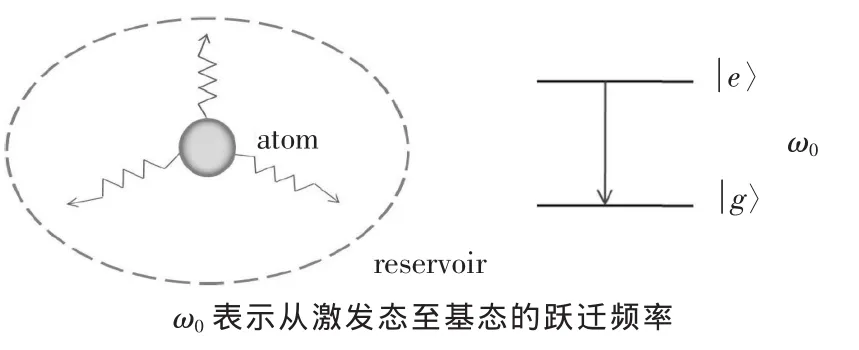
图1 两能级原子自发衰变的物理模型

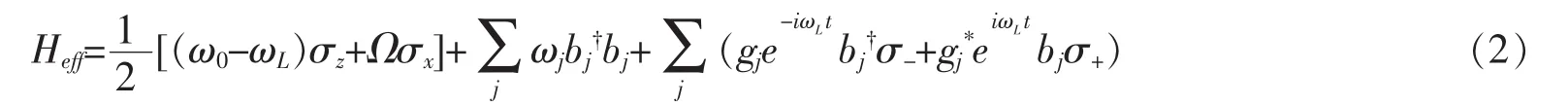
其中，σx=（1/2）（σ++σ-）。 为了简化计算，可以把系统的哈密顿量进行对角化处理为，其中。在系统与环境弱耦合条件下，含时演化态ρt满足量子主方程

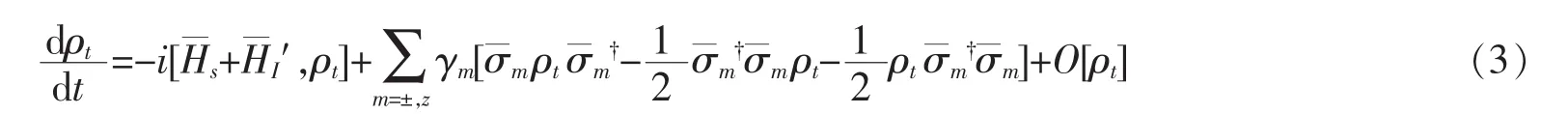
其中，相互作用哈密顿量在该表象可表示为

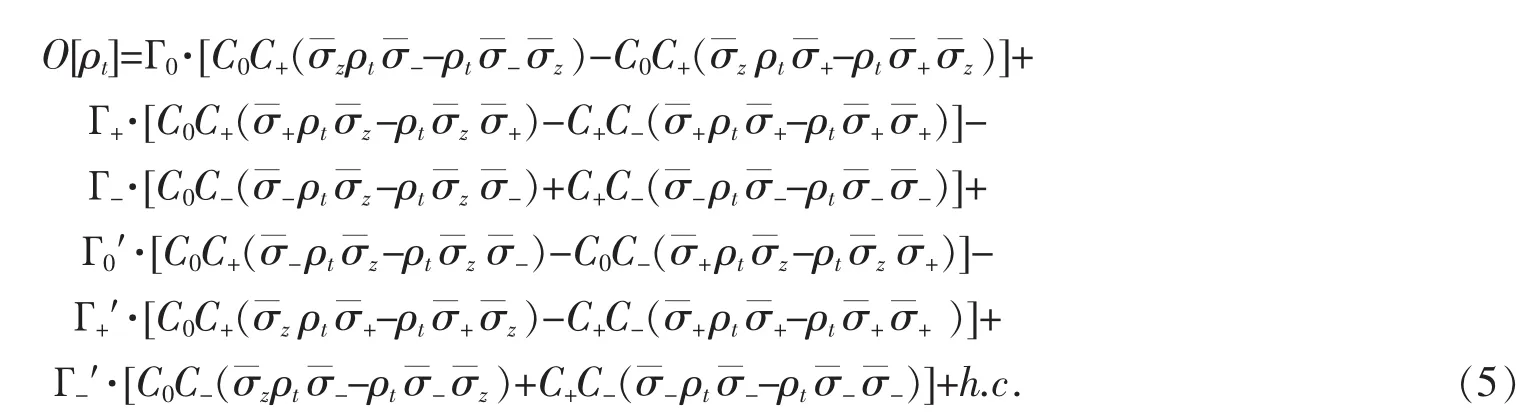
上式符号h.c.表示厄米共轭项。拉姆位移哈密顿量HI′描述了系统哈密顿量Hs特征向量的能量小部分转移，由于其没有对系统的退相干过程产生实质性影响，因此，在计算时可忽略。需要注意的是，该方程的高频震荡项已被忽略，其值非常小，这在弱耦合情况下是合理的[21-22]。

衰减率 γm（t）（m=±，z）与时间相关联，被定义为Re 表示取实数部分。参数为

外部环境可以由有效洛伦兹频谱函数来描述

其中，γ0衡量耦合作用强度，λ为频谱宽度。γ0＜（1/2）λ为弱耦合条件，因此，接下来的探讨都是在该情况下展开的。对于单比特，任意时刻的演化态ρt都可以由泡利矩阵表示为

其中 I为单位算符，σk（k=x，y，z）为泡利算符。 如图 2 所示，Bx（t）、By（t）、Bz（t）分别代表布洛赫球的三个方向矢量，它们与衰减率γm的关系由方程组给出

图2 布洛赫球模型

解得 Bx（t）、By（t）、Bz（t）与时间的关系式

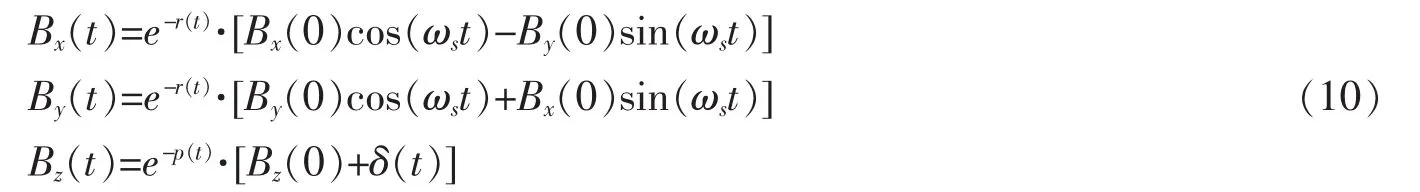
2 计算与分析

衡量量子演化时间的主要依据在于如何有效区分量子态。利用量子态迹间距Trace distance区分量子初态和末态，其定义为

和Bures angle[17]方法类似的，在冯·诺依曼迹不等式与柯西-许瓦尔兹不等式的约束下，得到量子演化极限QSLT表达式

如果激发态|e〉作为系统演化时的初态，那么有 Bx（0）=By（0）=0，Bz（0）=1，这就意味着 Bx（t）=By（t）=0。 随时间变化的量子态ρt可以简化为

假设量子系统经过驱动时间τD从初态ρ0演化到末态，通过数值计算绘制出图3曲线。参数取值分别为τD=3，λ=1，T=0，γ0=0.1，ω0=1。

从图3观察到，如果撤去电场，即Ω=0，那么原子系统只受到环境的弱耦合作用，无法加速，τQSL=τD始终成立。当电场频率ωL=1时，随着电场强度Ω的增加，比值τQSL/τD呈现起伏式的下降。当电场频率上升到5或10的时候，缓慢加强电场对原子作用，τQSL/τD会陡峭下降，然后再变大。因此，要合理调整参数ωL和Ω，来达到加速系统演化的目的。

为了分析量子系统演化在局域电场调控下的加速行为，有如下表达式

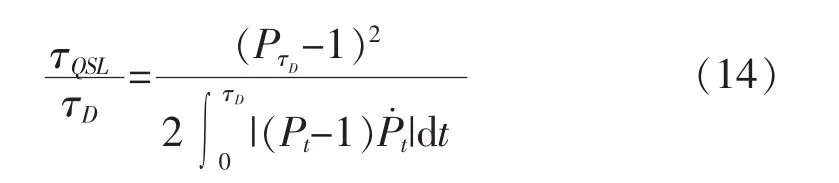
图3 量子演化极限时间在不同电场频率下随电场强度的变化曲线

很明显地，从图4可以看出，当电场的频率稳定时，加强电场对原子系统的作用，来抑制量子退相干，从而加速量子演化。

3 结语

在温度T=0时，通过局域电场调控阻尼衰减的Jaynes-Cummmings模型。通过量子主方程，获得在弱耦合时开放系统的演化规律。虽然系统与环境弱耦合时演化没有加速，但是选取合适的电场频率和电场对原子的作用强度有利于加速量子演化。将经典场运用到量子领域，为促进量子演化提供了新的方案。

图4 激发态占有数Pt在电场强度Ω=2，6时随时间的变化曲线

[1]BEKENSTEIN J D.Energy cost of information transfer[J].Physical Review Letters，1981，46：623.

[2]GIOVANNETTI V，LLOYD S，MACCONE L.Quantum metrology[J].Physical Review Letters，2006，96：010401.

[3]CANEVA T，MURPHY M，CALARCO T，et al.Optimal control at the quantum speed limit[J].Physical Review Letters，2009，103：240501.

[4]FLEMING G N.A unitarity bound on the evolution of nonstationary states[J].Nuovo Cimento A，1973，16：232.

[5]ANANDAN J，AHARONOV Y.Geometry of quantum evolution[J].Physical Review Letters，1990，65：1697.

[6]VAIDMAN L.Minimum time for the evolution to an orthogonal quantum state[J].American Journal of Physics，1992，60：182.

[7]LEVITIN L B，TOFFOLI T.Fundamental limit on the rate of quantum dynamics：the unified bound is tight[J].Physical Review Letters，2009，103：160502.

[8]JONES P J，KOK P.Geometric derivation of the quantum speed limit[J].Physical Review A，2010，82：022107.

[9]ZWIERZ M.Comment on “Geometric derivation of the quantum speed limit”[J].Physical Review A，2012，86：016101.

[10]DEFFNER S，LUTZ E.Energy-time uncertainty relation for driven quantum systems[J].Journal of Physics A，2013，46：335302.

[11]TADDEI M M，ESCHER B M，DAVIDOVICH L，et al.Quantum speed limit for physical processes[J].Physical Review Letters，2013，110：050402.

[12]CAMPO A D，EGUSQUIZA I L，PLENIO M B，et al.Quantum speed limits in open system dynamics[J].Physical Review Letters，2013，110：050403.

[13]XU Z Y，LUO S，YANG W L，et al.Quantum speedup in a memory environment[J].Physical Review A，2014，89：012307.

[14]DEFFNER S.Optimal control of a qubit in an optical cavity[J].Journal of Physics B，2014，47：145502.

[15]MARGOLUS N，LEVITIN L B.The maximum speed of dynamical evolution[J].Physica D：Nonlinear Phenomena，1998，120D：188.

[16]ZHANG Y J，HAN W，XIA Y J，et al.Quantum speed limit for arbitrary initial states[J].Scientific Reports，2014，4：4890.

[17]DEFFNER S，LUTZ E.Quantum speed limit for non-markovian dynamics[J].Physical Review Letters，2013，111：010402.

[18]FROWIS F.Kind of entanglement that speeds up quantum evolution[J].Physical Review A，2012，85：052127.

[19]LIU C，XU Z Y，ZHU S Q.Quantum-speed-limit time for multiqubit open systems[J].Physical Review A，2015，91：022102.

[20]WU S X，ZHANG Y，YU C S，et al.The initial-state dependence of quantum speed limit[J].Journal of Physics A，2015，48：045301.

[21]HAO X，WANG X Q，LIU C，et al.Finite-temperature decoherence of spin states in a Cu3single molecular magnet[J].Journal of Physics B，2103，46：025502.

[22]HAO X，TONG N H，ZHU S Q.Dynamics of quantum fisher information in a spin-boson model[J].Journal of Physics A，2013，46：355302.

Quantum speed limit driven by local electric field

WU Wenjiong， YAN Kai， XIE Yanqing，HAO Xiang*
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

We apply a local electric field to accelerate the quantum evolution in the decoherence model of a two-level atom weakly coupled to a structural reservoir at zero temperature.Under the time-convolutionless master equation，we obtained the decoherence process of the open system.The quantum evolution is related to the frequency and the driving strength of the electric field.From the perspective of the excited population，we interpreted the quantum speed limit.

decoherence；quantum speed limit；local electric field

O441.4

A

2096-3289（2017）03-0041-04

责任编辑：李文杰

2016-03-02

国家自然科学基金重点资助项目（11274054）；江苏省研究生培养创新工程项目（JGLX15-150）；苏州科技大学研究生科研创新项目（SKYCX16_015）

吴文炯（1991-），男，江苏苏州人，硕士研究生，研究方向：量子光学与微结构光子学。

*通信作者：郝 翔（1981-），男，博士，副教授，硕士生导师，E-mail：haoxiang_edu198126@163.com。