频率调控液体变焦透镜
2017-09-11邹异,李华*,曹洋,谢鸥,殷振
邹 异,李 华*,曹 洋,谢 鸥,殷 振
(1.苏州科技大学 数理学院,江苏 苏州 215009;2.河南工业大学 机电工程学院,河南 郑州 450007)
频率调控液体变焦透镜
邹 异1,李 华1*,曹 洋2,谢 鸥1,殷 振1
(1.苏州科技大学 数理学院,江苏 苏州 215009;2.河南工业大学 机电工程学院,河南 郑州 450007)
为了实现透镜的微型化、无机械组件和可变焦距,设计了超声压电陶瓷驱动液体变焦透镜。超声液体透镜由压电陶瓷、封装薄膜和铝制包层组成。液体透镜的变焦由输入电源的频率调控。通过数字图像处理技术提取液体透镜的面型参数后,运用多项式拟合得到透镜的面型函数。利用Matlab仿真得到透镜的内外焦距、焦距差和光路追迹图。推动了超声液体透镜的研究进展,为超声液体透镜走向实用化提供了理论基础。
光学仪器;液体透镜;频率控制;光学变焦;图像处理
随着人们对镜头要求的日益提高,传统变焦透镜结构复杂、制造和设计成本高昂、难以实现微型化的缺点日益突出,液体变焦透镜作为一种新型的变焦光学元件成为研究热点。经过多年发展,液体透镜的实现形式也呈现多样化趋势[1-2]。液体透镜比较成熟的实现形式目前有两种:第一种是通过改变液面形状实现变焦,如基于电润湿效应的可变焦透镜[3-7]是通过改变液体表面电荷分布来改变液体与接触面的接触角,从而实现液面变形;充液式液体透镜[8]是依据液体难以被压缩、体积守恒的原理,通过改变透镜内部的液体体积来改变液面形状。第二种是通过改变液体折射率实现变焦,如液晶变焦透镜[9-10]通过施加电压改变液晶的折射率,在不改变透镜形状的情况下实现变焦。
笔者介绍了一种超声液体变焦透镜的基本结构[11-14]。通过超声振动仿真和测试得到了超声透镜的工作频率,运用图像处理技术实现了对液体变焦透镜面型参数的提取,把面型函数拟合成了多项式。在Matlab中对透镜的成像性能进行了模拟仿真,得到透镜的焦距以及光路追迹图。
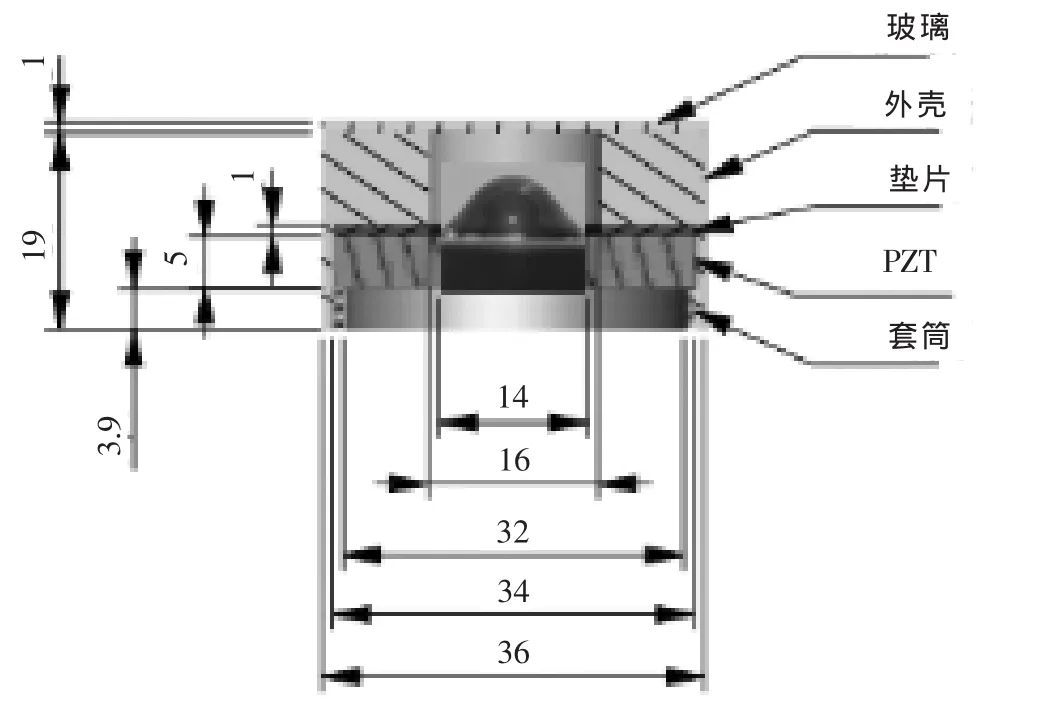
图1 液体透镜结构示意图
1 超声液体透镜系统的分析
笔者设计的变焦透镜结构如图1所示。中心位置是一个环形压电陶瓷片,陶瓷片中心用光学薄膜密封,腔内封装液体,顶部用光学平板玻璃密封,外部是铝制包层。空腔中的液体选择折射率1.333的纯水。实验采用单片压电陶瓷激励,负载对压电陶瓷的工作状态将会产生比较大的影响,压电片用软橡胶垫圈固定,压电陶瓷采用边缘支撑,有效减少压电陶瓷的无用负载,使得压电陶瓷可以稳定高效的对外做功。
压电透镜的振动分为压电陶瓷的振动和薄膜的振动,笔者对圆形薄膜振动和压电振动做了研究。
1.1 圆形薄膜的弯曲振动
由于压电陶瓷环下表面的薄膜使用环氧树脂胶与压电陶瓷环相粘结,薄膜相当于一个边界固定的圆盘面,且圆盘面的厚度是均匀的。薄膜的振动是受到压电振子激励产生的,压电振子的工作频率就是薄膜的振动频率。
对于圆盘振动的研究,课题组曾推导固定边界圆盘的振动方程[15]。国内对圆盘振动的研究也很多[16-19]。
圆盘受到周边简谐位移激励

其中ωn为圆盘的n阶谐振频率。当圆盘处在谐振频率上时

式中AnJ0(knr)+BnI0(knr)为圆盘轴对称弯曲振动的振型,J0、I0分别为第一类贝塞尔函数和第一类变形贝塞尔函数;r为圆盘上点到圆心的距离;ρp、h、Ep、ν、D分别为圆盘的材料密度、厚度、弹性模量、泊松比和弯曲刚度系数,An、Bn为待定系数。
在固定边界条件下的频率方程为[15-16]

经过计算(4)式得到薄圆盘振动的共振频率为

其中a为圆盘的半径,h为圆盘的厚度,n为正整数。
薄膜参数特性见表1。将表1中的薄膜数据代入弯曲振动薄圆环的频率方程可求kna的值,n为节圆数。
表1数据代入(5)式经过计算得到圆盘的前三阶振动模态的共振频率,结果见表2。

表1 薄膜参数特性

表2 共振频率计算结果
1.2 压电陶瓷谐振频率测量
在PZT环的上下表面电极间施加一个连续高频正弦电压作为驱动激励。
用阻抗分析仪PV70a检测分析组装好的液体透镜,测试得到了不同液体透镜在压电振子谐振状态下的导纳圆图,结果如图2所示。

图2 导纳圆图
表3列出压电陶瓷的具体参数,在43 kHz和145 kHz附近压电振子处于谐振状态,对于不同负载下的液体透镜,压电陶瓷的谐振频率基本一致。通过对比表3中43 kHz和145 kHz的检测数据可知压电振子在145 kHz时动态电阻更小,机械品质因数和机电转换效率更高,所以选定145 kHz为最佳工作频率。

表3 压电陶瓷性能参数
2 面型仿真与检测
2.1 液体透镜面型提取
透镜制作封装后,在压电陶瓷圆环的正负电极间施加一个正弦交变电压,由于压电陶瓷在工作中电阻值不是定值,所以激励电源的电压值也无法完全稳定,而信号发生器的频率可以准确调节,所以选用电源频率调节来控制液体透镜。实验检测了水透镜在输入电压为100 V时改变输入电源频率时的表面面型。图3是输出电压稳定在100 V时液体透镜在不同频率激励下的表面形貌。
在液体表面张力、液体重力以及超声振动的声场辐射力的作用下,液体的表面会随着声场辐射力的大小发生变化。由于超声压电陶瓷的高频输出特性,液体透镜的弛豫时间远大于输入电压的一个周期,透镜的表面在没有其他外界扰动时处于稳定状态,可以保证持续成像。
2.2 成像性能仿真
将液体透镜的表面形貌进行图像处理之后得到液面边缘的图像信息。由于液面是一个非球面,用高阶多项式拟合得到液面的函数表达式。
在Matlab中对液体透镜在不同驱动频率下面型进行光线追迹分析。图4中给出了光线追迹的结果。

图3 液体透镜透镜表面形貌

图4 光线追迹结果
简单分析图4,发现:(1)液体透镜在单一频率电压驱动下,透镜的不同区域的焦距并不相同;(2)在距离主光轴半径距离相同时,透镜的焦距基本一致;(3)平行光入射时,透镜对光线具有汇聚作用,在驱动电压频率143 kHz时,透镜的焦距最小,透镜中央的焦距一致。选取透镜主光轴处为内焦距,将透镜边缘焦距称为外焦距。
表4给出了具体的透镜焦距。

表4 液体透镜焦距
图5给出了透镜内外焦距和驱动电压频率的变化曲线。分析图5曲线发现:(1)驱动电压频率在135 kHz到145 kHz时,随着驱动电压频率升高透镜内焦距变小;(2)驱动电压频率在135 kHz到145 kHz时随着驱动电压频率升高透镜外焦距不稳定,呈震荡变化趋势。
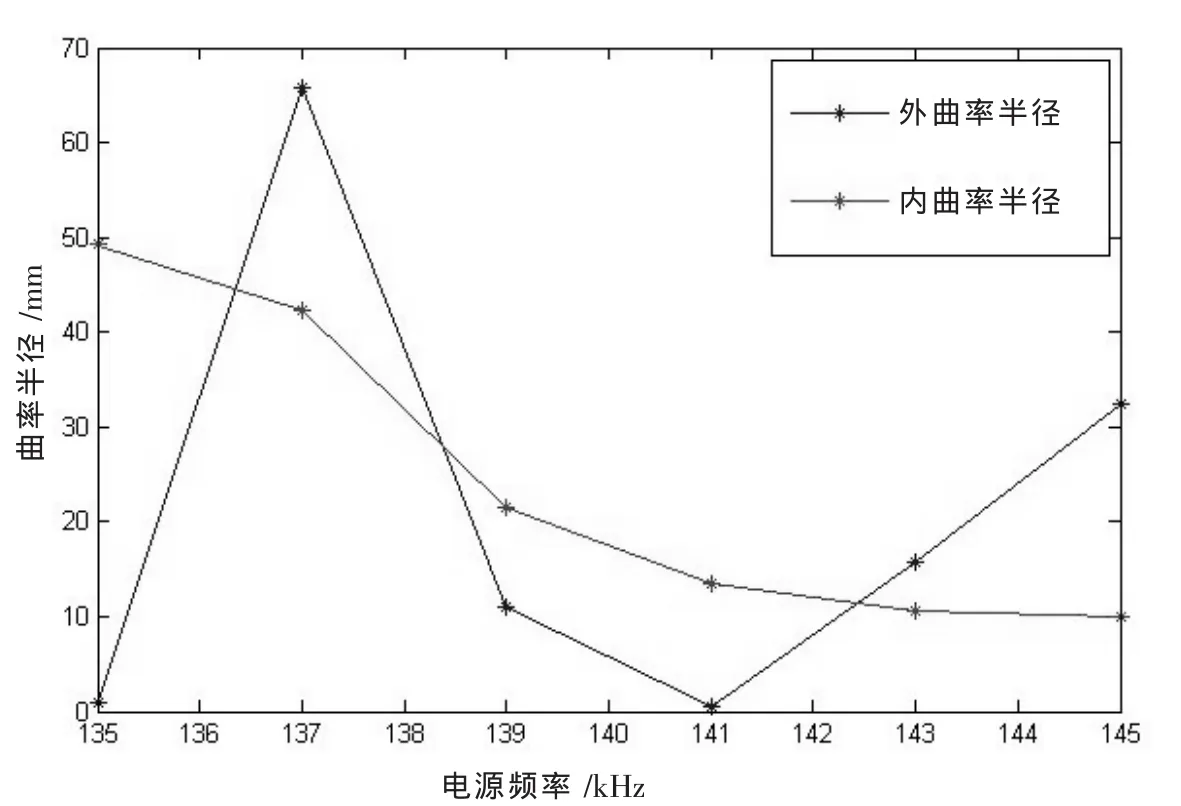
图5 透镜内外焦距和驱动电压频率的变化曲线
3 结语
根据液体透镜的微型化、集成化、材料低成本和无机械组件的要求,研制了一种基于压电驱动的液体变焦透镜,研究了压电透镜的工作机理和机构特点。通过压电振动理论和薄膜振动理论确定了压电振子的最佳工作频率为145 kHz。检测了透镜面型数据后分析得到透镜的内外焦距、中心位移。在143 kHz时,透镜的内外焦距基本一致。
超声压电透镜也存在一些问题。由于重力的存在,光轴不稳定,成像效果也未达到高清。在透镜结构、透镜材料和电源驱动方面可做如下改进:(1)缩小透镜口径的尺寸,以降低重力对液体透镜光轴的影响;(2)透镜尽量选择水平放置;(3)选择表面张力更大、折射率更大的填充液体(离子液体),扩大变焦范围;(4)在薄膜上加入补偿装置,以求矫正液体透镜边缘的像差。
[1]李零印,王一凡.液体变焦技术的反发展与展望[J].中国光学,2012,5(6):578-582.
[2]张鹰,张新,史广维,等.液体透镜在变焦系统中的应用[J].中国光学,2013,6(1):46-55.
[3]焦娇.液体变焦透镜的EWOD特性和电场仿真研究[D].南京:南京邮电大学,2012.
[4]胡晓东,曲超,张世国,等.电润湿离子液体变焦透镜[J].光电工程,2012,39(2):53-58.
[5]万静,梁忠诚.基于EWOD的微流控透镜变焦特性分析[J].光学技术,2009,35(6):919-923.
[6]徐元涛,陈家璧.双液体变焦透镜像差的测量研究[J].光学仪器,2013,35(4):38-42.
[7]REN Hongwen,WU Shintson.Variable-focus liquid lens[J].Optics Express,2008,15(10):1397-1402.
[8]王春水,张斌珍,龚珊,等.充液型可调双焦微透镜的设计与仿真[J].电子器件,2013,36(5):608-611.
[9]刘俊江,李恩普.基于数字全息显微术的液体透镜参数测量方法[J].中国激光,2014,41(11):1-6.
[10]郑继红,王雅楠.液晶微透镜技术研究新进展[J].光学仪器,2014,36(2):182-188.
[11]KOYAMA D,ISAGO R,NAKAMURA K.Compact,high-speed variable-focus liquid lens using acoustic radiation force[J].Optics Express,2010,11(22):25158-25169.
[12]KOYAMA D,HATANAKA M,NAKAMURA K,et al.Ultrasonic optical lens array with variable focal length and pitch[J].Optics Letters,2012,37(24):5256-5258.
[13]KOYAMA D,ISAGO R,NAKAMURA K.Ultrasonic variable-focus optical lens using viscoelastic material[J].Appl Phys Lett,2012 (100),091102.
[14]KOYAMA D,NAKAMURA K.Ultrasonic high-speed variable-focus optical lens[J].IEEE Global Conference on Consumer Electronics,2012,1:54-55.
[15]李华,任坤,殷振,等.纵弯转换超声振动球面聚焦系统聚焦特性研究[J].压电与声光,2014(3):450-454.
[16]张小丽,林书玉,付志强,等.弯曲振动薄圆盘的共振频率和等效电路参数研究[J].物理学报,2013,62(3):34301-34306.
[17]潘晓娟,贺西平.厚圆盘弯曲振动研究[J].物理学报,2010,59(11):7911-7916.
[18]贺西平.弯曲振动阶梯圆盘辐射阻抗的计算方法[J].物理学报.2010,59(5):3290-3293.
[19]宁景锋,贺西平,李娜,等.纵振激励频率对圆盘弯曲振动特性的影响[J].振动与冲击,2011,30(4):100-102.
Variable-focus liquid lens using frequency control
ZOU Yi1, LI Hua1*, CAO Yang2,XIE Ou1, YIN Zhen1
(1.School of Mathematics and Physics,SUST,Suzhou 215009,China;2.School of Mechanical and Electrical Engineering,Henan University of Technology,Zhengzhou 450007,China)
In order to design the micro-scale lens of no mechanical components and variable focal length,a new kind of high-speed variable-focus liquid lens using acoustic radiation force was provided.The liquid lens consisted of thin piezoelectric ceramic ring,packaging film and aluminum cladding.The liquid lens realized changes in focal lengths by means of controlling the frequency of power sources.Based on digital image processing techniques,the image surface of lens was calculated.Using polynomial fit technique,we obtained the surface function of lens.The outer-side focal length,focal length differences and ray tracing were also simulated by Matlab.This study promoted the development of liquid lens and paved the way for the practice of variable-focus micro-lens.
optical instrument;liquid lens;frequency control;optical zoom;picture processing
O439
A
2096-3289(2017)03-0045-05
责任编辑:李文杰
2015-12-26
邹 异(1991-),男,江苏无锡人,硕士研究生,研究方向:超声液体透镜。
*通信作者:李 华(1961-),男,教授,博士,硕士生导师,E-mail:lihua@mail.usts.edu.cn。
