时间尺度上事件空间中Birkhoff系统的Noether定理

施玉飞，张 毅

（1.苏州科技大学 数理学院，江苏 苏州 215009；2.苏州科技大学 土木工程学院，江苏 苏州 215011）

时间尺度上事件空间中Birkhoff系统的Noether定理

施玉飞1，张 毅2*

（1.苏州科技大学 数理学院，江苏 苏州 215009；2.苏州科技大学 土木工程学院，江苏 苏州 215011）

研究时间尺度上事件空间中Birkhoff系统的Noether对称性与守恒量。首先，提出并建立时间尺度上事件空间中Birkhoff系统的变分问题；然后，求得时间尺度上事件空间中Birkhoff系统的参数方程；最后，基于Pfaff作用量在无限小变换下的不变性，给出了时间尺度上事件空间中Birkhoff系统的Noether对称性的定义，利用时间重新参数化方法，求得时间尺度上事件空间中Birkhoff系统的Noether定理并举例说明其应用。

时间尺度；事件空间；Birkhoff系统；对称性；守恒量

1988年，Hilger[1]首次提出时间尺度上的微积分理论，定义在时间尺度上的微积分将离散的差分方程和连续的微分方程进行了统一和扩展。2004年，Bohner[2]首次讨论了时间尺度上的变分问题。1918年，Noether首次研究了Hamilton作用量在无限小变换下的不变性，即Noether对称性[3]。Noether定理揭示了在无限小变换下变分不变性与守恒量之间的关系。2007年，Bartosiewicz和Torres[4]首次得到了在时间尺度上的Noether定理。国内学者也分别在连续和离散系统下对Noether理论进行了研究[5-8]。而对时间尺度上的Noethe理论研究才刚刚起步，如蔡平平、傅景礼和郭永新首次给出了在时间尺度上非保守非完整系统的Noether理论[9]，张毅得到了在Hamilton系统中Noether对称性与守恒量[10]，宋传静和张毅首次研究了在 Birkhoff系统的Noether对称性与守恒量[11]，祖启航和朱建青探讨了在非完整系统上的Noether理论[12-13]。

事件空间是指将时间也作为一个变量，把原来n维位形空间扩展到n+1维空间，这样时间变量与坐标变量在系统中处于同一地位。学者们分别在离散和连续系统下，研究了事件空间中的对称性问题[6，14-18]。为了更好的探究Birkhoff系统的一般物理实质，笔者进一步研究时间尺度上事件空间中Birkhoff系统的Noether理论，即将离散系统与连续系统统一起来，并且在时间与坐标变量处于同一地位下，即在时间尺度上事件空间中研究Birkhoff系统的Noether对称性与守恒量。首先，求得时间尺度上事件空间中Birkhoff系统的参数方程；然后，给出时间尺度上事件空间中Birkhoff系统的Noether对称性的定义，并且利用时间重新参数化方法，求得时间尺度上事件空间中Birkhoff系统的Noether定理。

1 时间尺度上的微积分

该节将简单介绍文中涉及到的时间尺度上的微积分。详细内容可参见文献[19]。

设 T是一个时间尺度，∀t∈T，向前跳跃算子 σ：T→T，σ（t）=inf{s|s＞t，s∈T}，当 supT＜+∞ 时，σ(supT)=supT；向后跳跃算子 ρ：T→T，ρ（t）=sup{s|s＜t，s∈T}，当 infT＞-∞ 时，σ（infT）=infT。 步差函数 μ：T→[0，+∞），μ（t）=σ（t）-t。

若 t＜σ（t），则称 t右离散；若 t=σ（t），则称 t右稠密。 若 ρ（t）＜t，则称 t左离散；若 ρ（t）=t，则称 t左稠密。

定义Tk为

函数 f：T→R，则定义 fσ：T→R，fσ（t）=f（σ（t））或者写成 fσ=f◦σ。

设 t∈Tk，函数 f：T→R，若对于任意 ε＞0，存在 δ＞0，使得对于任意的 t，s∈U，这里的 U=（t-δ，t+δ），有

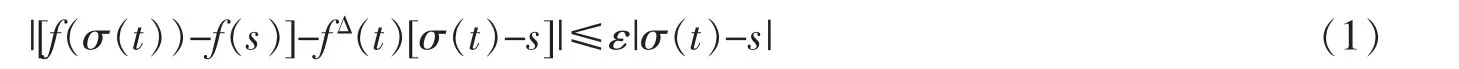
则称 fΔ（t）为 Δ-导数，这里 fΔ（t）=Δf（t）/Δt。

如果函数f：T→R在T的右稠密点处连续，并且在T的左稠密点处左极限存在，则称函数f在T上是rd-连续。记为Crd。若函数f：T→R上Δ-可微，且其Δ-导数是右连续的，则记为；若函数f：T→R二阶 Δ-可微，并且二阶Δ-导数是右连续的，则记为

如果函数 f：T→R 是右稠密的，对任意的 t∈Tk，若存在 F，有 FΔ（t）=f（t），定义不定积分为C其中C为任意常数，则定积分为：对任意的a，b∈T，有

函数 f：[a，b]T→R 上连续且有 Δ-导数，若 fΔ（t）＞0，则 f（t）在时间尺度[a，b]T单调递增[20]。

文中将用到的几个重要公式

时间尺度上 Dubois-Reymond 引理[21]：令 g∈Crd，g：[a，b]→Rn，如果对任意的，且 η（a）=η（b）=0，都有，则 g（t）=C，其中常数 C∈Rn。

2 时间尺度上事件空间中Birkhoff系统的参数方程

研究事件空间中Birkhoff系统，其Birkhoff变量为aλ（λ=1，…，2n）。建立（2n+1）维事件空间，其空间中点的坐标为 aλ（λ=1，…，2n）和 t。

记

则变量 xα（α=1，…，2n+1）都可以作为某参数 τ的已知函数。 令 xα=xα（τ）是类曲线，使得当

不同时为零时，有

假设系统在位形空间中的 Birkhoff函数为 B（t，aλ），Birkhoff函数组为 Rγ=Rγ（t，aλ）（γ=1，…，2n），则事件空间中的 Birkhoff函数组为 Bv（xα）（v=1，…，2n+1），其中

事件空间中Pfaff作用量为[16]

则在时间尺度上事件空间中，式（12）的被积函数可定义为

则时间尺度上事件空间中系统的Pfaff作用量可表为

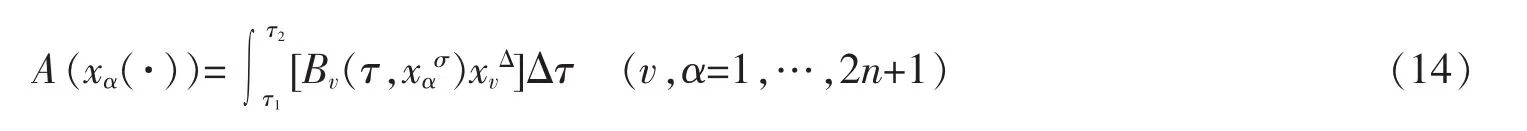
则时间尺度上事件空间中的Pfaff-Birkhoff原理可表为

且满足交换关系

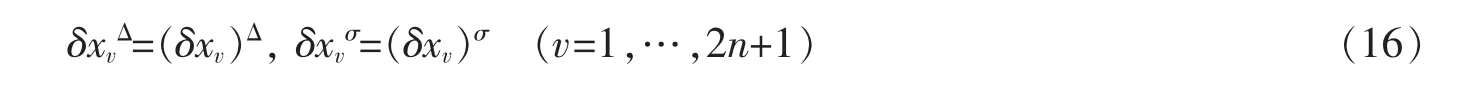
和端点条件

现在将式（15）进行变换，有

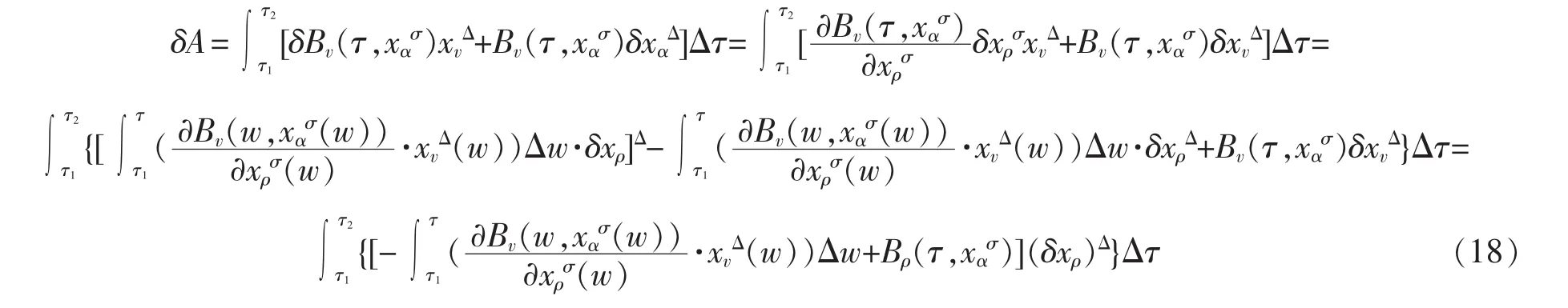
由时间尺度上Dubois-Reymond引理，得到

对式（19）求 Δ－导数，得

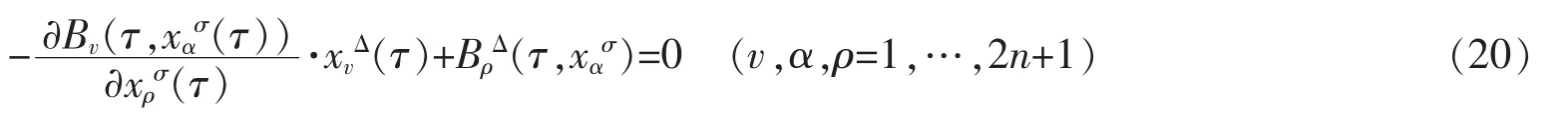
式（20）可称为时间尺度上事件空间中Birkhoff系统的参数方程。

3 时间尺度上事件空间中Birkhoff系统的Noether定理

接下来建立时间尺度上事件空间中Birkhoff系统的Noether定理。定理的证明分为两步：第一步是在参数τ不变的无限小变换下给出证明；第二步利用时间重新参数化方法证明在参数τ变化的无限小变换下的Noether定理。

首先，在参数τ不变时，引入无限小变换群

定义 1 如果 Pfaff作用量（14）在无限小变换（21）作用下，对于任意的子区间[τa，τb]⊆[a，b]，其中 τa，τb∈T，满足

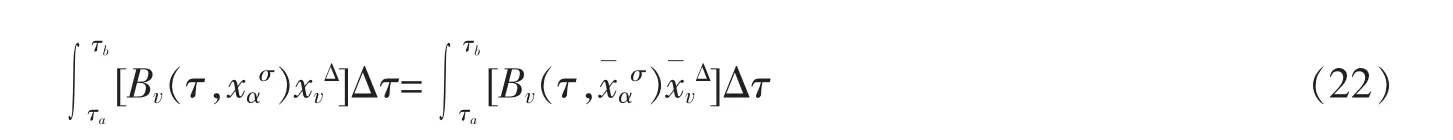
则称这种不变性为时间尺度上事件空间中Birkhoff系统在参数τ不变的无限小变换（21）下的Noether对称性。

定理1 如果Pfaff作用量（14）在无限小变换（21）作用下保持不变，则对于一切τ∈[a，b]成立

证明 因为 Pfaff作用量（14）在无限小变换（21）作用下保持不变，则式（22）对于任意的子区间[τa，τb]⊆[a，b]都保持不变，所以式（22）等价于

将无限小变换（21）代入（24），得

在式（25）两边对 ε 求导，并令 ε＝0，得式（23）。

式（23）可称为时间尺度上事件空间中Birkhoff系统在参数τ不变的无限小变换（21）下的Noether等式。

定理2 在时间尺度上事件空间中Birkhoff系统中，如果Pfaff作用量（14）在无限小变换（21）变换下保持不变，则系统的守恒量为

证明 应用式（20）和式（23）

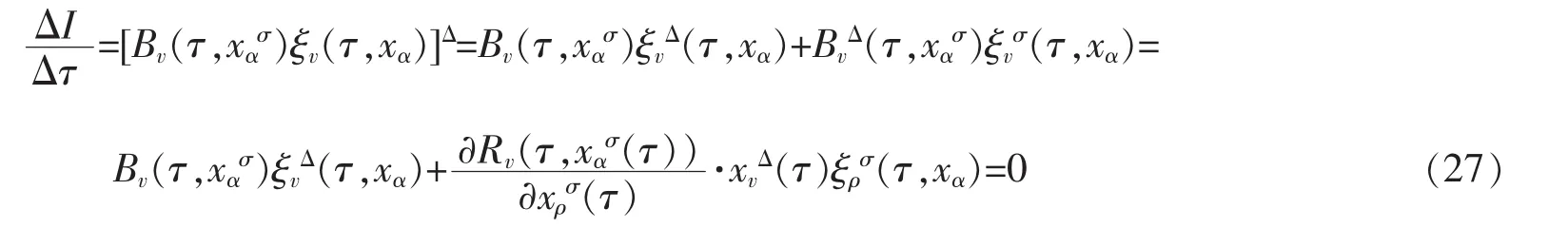
因此，证得式（26）。

其次，在参数τ变化时，引进无限小变换群

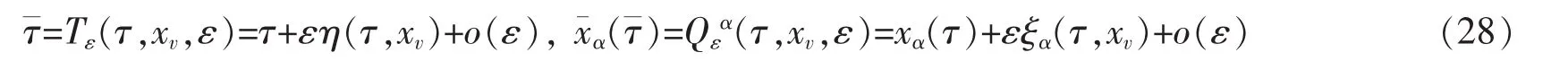
设映射β

定义 2 如果 Pfaff作用量（14）在无限小变换（28）作用下，对于任意的子区间[τa，τb]⊆[a，b]，其中 τa，τb∈T，满足

则称这种不变性为时间尺度上事件空间中Birkhoff系统在无限小变换（28）下的Noether对称性。

定理3 如果Pfaff作用量（14）在无限小变换（28）下保持不变，则对于一切τ∈[a，b]有

成立。式（32）可称为时间尺度上事件空间中Birkhoff系统的Noether等式。

证明 由式（31）

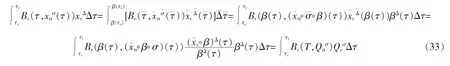
因为区间[τa，τb]是[a，b]的任意子区间，上式等价于

在式（34）两边对 ε 求导，并令 ε=0，

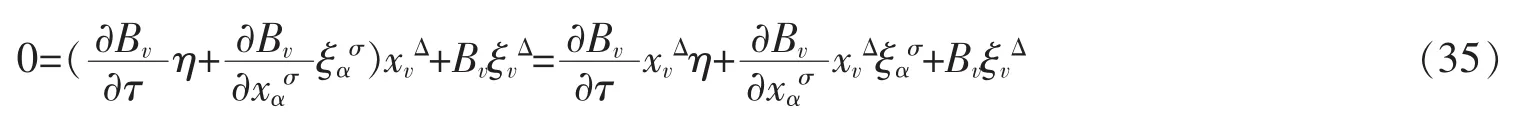
因此，式（32）可称为时间尺度上事件空间中Birkhoff系统的Noether等式。

定理4 在时间尺度上事件空间中Birkhoff系统中，如果Pfaff作用量（14）在无限小变换（28）下保持不变，则系统的守恒量为

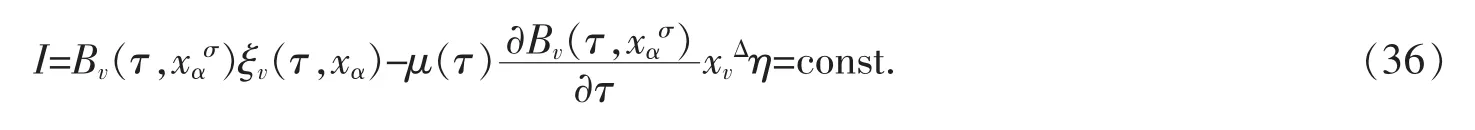
证明 令

当 s（τ）＝τ时，有

由定义 2，当 s（τ）＝τ时，有

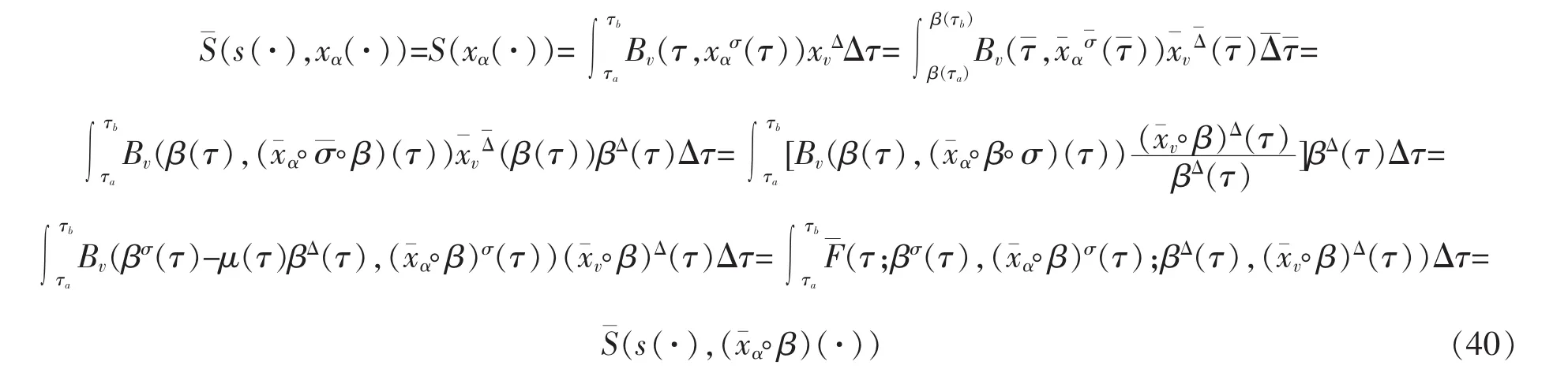
当 s（τ）＝τ时，有

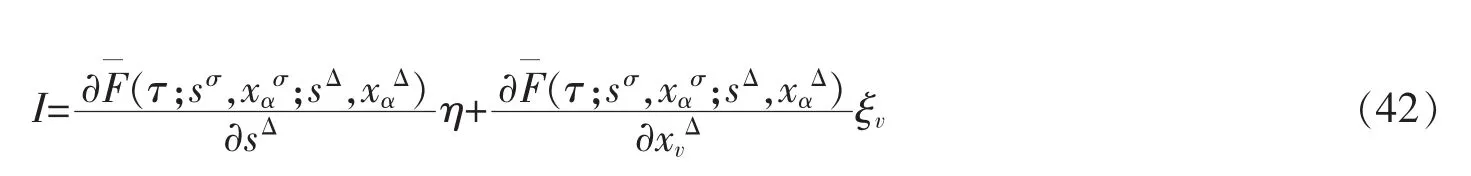
是一个守恒量。其中

和

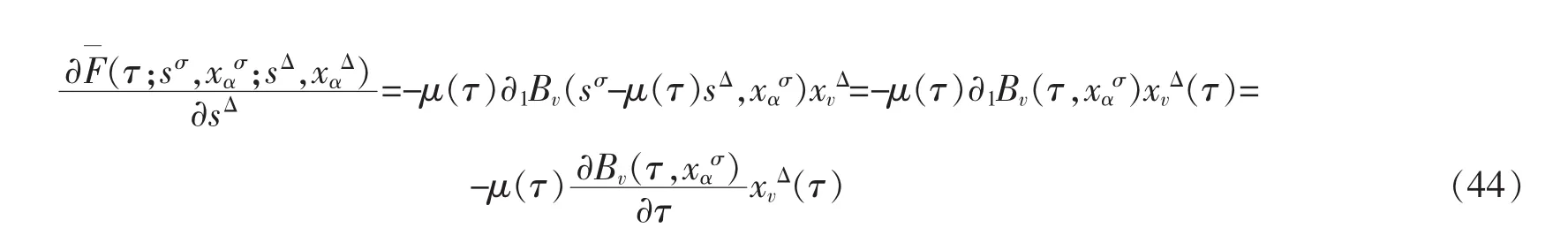
将式（43）和（44）代入（42），即可得到定理 4。

当 T=R时，则 σ（τ）＝τ，μ（τ）=0，则守恒量（36）转化为经典的事件空间中 Birkhoff系统的 Noether守恒量[16]

当 T=hZ 时，h＞0，则 σ（τ）=τ+h， μ（τ）=h，则守恒量（36）转化为离散的事件空间中 Birkhoff系统的Noether守恒量

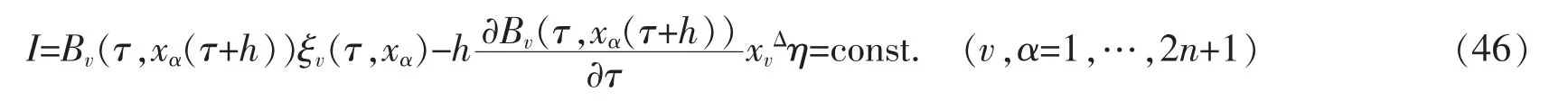
当τ=t时，则参数方程（20）的后面2n个方程

为时间尺度上的Birkhoff方程，守恒量（36）转化为经典的时间尺度上Birkhoff系统的Noether守恒量[11]

当T=R且τ=t，则时间尺度上的Birkhoff系统方程（47）转化为经典的位形空间中的Birkhoff方程

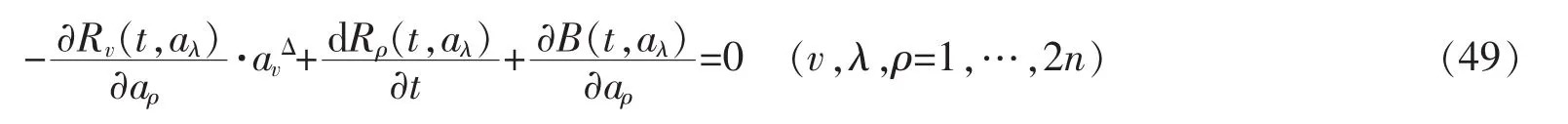
守恒量（36）转化为经典的Birkhoff系统的Noether守恒量

4 算例

第一步，求出向前跳跃算子 σ（τ）和步差函数 μ（τ），

第二步，由式（11），求得时间尺度上事件空间中的Birkhoff函数组

第三步，研究系统的Noether对称性，由式（33）得出Noether等式为

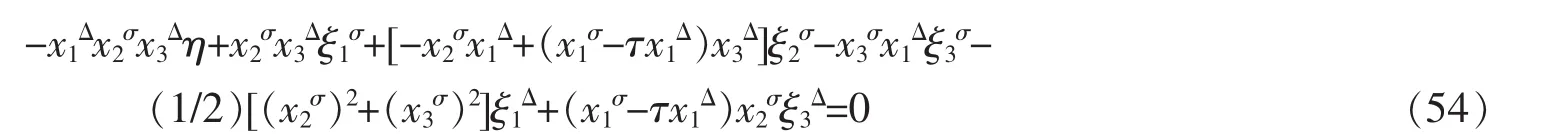
式（54）有一组解为

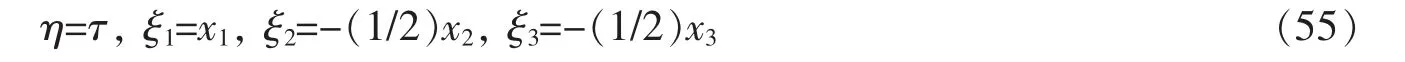
式（55）相应于系统的Noether对称性。将式（55）代入式（36），得相应守恒量为

式（56）就是由Noether对称性（54）导致的守恒量。

5 结语

时间尺度上事件空间中动力学系统的对称性与守恒量研究具有重要理论和实际意义。但由于现实问题的复杂性，时间尺度上事件空间中动力学系统的对称性研究才刚刚开始。文章研究了时间尺度上事件空间中Birkhoff系统的Noether定理。主要工作有：提出并建立了时间尺度上事件空间中Birkhoff系统的变分问题；得到了时间尺度上事件空间中Birkhoff系统的参数方程；研究了时间尺度上事件空间中Birkhoff系统的Noether对称性与守恒量，并结合一个算例说明其应用。文中方法和结果可进一步拓展到非保守问题以及非完整力学系统等。

[1]AULBACH B，HILHER S.A unified approach to continuous and discrete dynamics[J].Qualitative Theory of Differential Equations，1988，53：37-56.

[2]BOHNER M.Calculus of variations on time scales[J].Dynamic Systems&Applications，2004，13（12）：339-349.

[3]NOETHER A E.Invariante Variationsprobleme[J].Gott Nachr，1918，KI，II：235-257.

[4]BARTOSIEWICZ Z，TORRES D F M.Noether’s theorem on time scales[J].Journal of Mathematical Analysis&Applications，2007，342（2）：1220-1226.

[5]李子平.约束系统的变换性质[J].物理学报，1981，30（12）：1659-1671.

[6]梅凤翔.李群李代数对约束力学系统的应用[M].北京：科学出版社，1999.

[7]金世欣，张毅.相空间中含时滞的非保守力学系统的Noether定理[J].中山大学学报（自然科学版），2014，53（4）：56-61.

[8]徐瑞丽，方建会，张斌.离散差分序列变质量Hamilton系统的Lie对称性与Noether守恒量[J].物理学报，2013，62（15）：241-247.

[9]CAI P P，FU J L，GUO Y X.Noether symmetries of the nonconservative and nonholonomic systems on time scales[J].Science China Physics，Mechanics&Astronomy，2013，56（5）：1017-1028.

[10]张毅.时间尺度上 Hamilton 系统的 Noether理论[J].力学季刊，2016，37（2）：214-224.

[11]SONG C J，ZHANG Y.Noether theorem for Birkhoffian systems on time scales[J].Journal of Mathematical Physics，2015，56（10）：102701.

[12]ZU Q H，ZHU J Q.Noether theorem for nonholonomic nonconservative mechanical systems in phase space on time scales[J].Journal of Mathematical Physics，2016，57（8）：082701.

[13]祖启航，朱建青.时间尺度上Nabla变分问题的非完整力学系统的Noether理论[J].中山大学学报（自然科学版），2017，56（1）：58-65.

[14]SYNGE J L.Classical Dynamics[M].Berlin：Springer，1960.

[15]张毅.事件空间中Birkhoff系统的参数方程及其第一积分[J].物理学报，2008，57（5）：2649-2653.

[16]张毅.事件空间中 Birkhoff系统的 Noether理论[J].物理学报，2008，57（5）：2643-2648.

[17]张伟伟，方建会，张斌.事件空间离散完整系统的Noether理论[J].动力学与控制学报，2012（2）：117-120.

[18]张晔，张毅，陈向炜.事件空间中Birkhoff系统的Mei对称性与守恒量[J].云南大学学报（自然科学版），2016，38（3）：406-411.

[19]BOHENER M，PETERSON A.Dynamic Equations on Time Scales：An Introduction with Applications[M].Boston：Birkhäuser，2001.

[20]GUSEINOV G S，KAYMAKCALAN B.On a disconjugacy criterion for second order dynamic equations on time scales[J].Journal of Computational&Applied Mathematics，2002，141：187-196.

[21]BOHNER M，PETERSON A.Advances in Dynamic Equations on Time Scales[M].Boston：Birkhäuser，2003.

Noether theorem for Birkhoffian system on time scales in event space

SHI Yufei1，ZHANG Yi2*
（1.School of Mathematics and Physics，SUST，Suzhou 215009，China；2.School of Civil Engineering，SUST，Suzhou 215011，China）

In this paper,we studied the Noether symmetry and the conserved quantity for a Birkhoffian system on time scales in event space.First,the variational problem for a Birkhoffian system on time scales in event space was proposed and established.Then,Birkhoffian equations on time scales in event space were obtained.Last,based upon the invariance of the Pfaff action on time scales under the infinitesimal transformations of a group,the definition of the Noether symmetry for a Birkhoffian system on time scales in event space was given.Using the technique of time-re-parameterization,we obtained the Noether theorem for Birkhoffian system on time scales in event space and illustrated the application of the theorem.

time scale；event space；Birkhoffian system；symmetry；conserved quantity

O316 MR（2010）Subject Classification：70H99

A

2096-3289（2017）03-0001-07

责任编辑：谢金春

2017-02-25

国家自然科学基金资助项目（11272227；11572212）；江苏省普通高校研究生科研创新计划资助项目（KYZZ 15_0349）；苏州科技大学研究生科研创新计划资助项目（SKCX15_063）

施玉飞（1989-），男，江苏盐城人，硕士研究生，研究方向：力学中的数学方法。

*通信作者：张 毅（1964-），男，博士，教授，博士生导师，E-mail：zhy@mail.usts.edu.cn。