Multiple solutions for a class of fourth-order two-point boundary value problems

XI Lijing，HUANG Yisheng

（1.School of Mathematics and Physics，SUST，Suzhou 215009，China；2.School of Mathematical Sciences，Soochow University，Suzhou 215006，China）

Multiple solutions for a class of fourth-order two-point boundary value problems

XI Lijing1，2，HUANG Yisheng2

（1.School of Mathematics and Physics，SUST，Suzhou 215009，China；2.School of Mathematical Sciences，Soochow University，Suzhou 215006，China）

We studied the existence of multiple solutions for the following fourth-order two-point boundary value problem u（4）（x）=λf（u（x）），x∈（0，1）；u（0）=u（1）=u″（0）=u″（1）=0，where λ＞0 is a parameter and f：R→R is a continuous function.By means of variational methods and the theory of critical points，we obtained the results on the existence of two nonzero solutions and infinitely multiple solutions

fourth-order boundary value problem；(PS)condition；critical point

1 Introduction and main results

Owing to the importance of higher order differential equations in Physics，existence and multiplicity of solutions for problems like the following fourth-order boundary value problem

have been extensively studied，see for examples，[1－6]and the references therein.In particular，in[1]，by applying the Morse theory，the authors obtained two nonzero solutions in C4[0，1]for Problem （1） if f∈C1satisfying f（0）=0，there exists a natural number m≥1 such that m4π4＜f′（0）＜（m+1）4π4，and there exist α and β∈R1with α＜π4/2 such thatIn[2]，the authors got a multiplicity result of solutions for Problem（1），where to guarantee the existence of three solutions by using the Amann three-solution theorem the authors assumed that f is increasing and imposed some conditions to ensure the existence of sub-solutions and super-solutions.In addition，in[1]and[3]，the authors obtained the existence of infinitely many solutions for Problem （1）if f is an odd function.And in[4]，by employing the cone expansion or compression fixed point theorem，authors also got two results on existence of infinitely many solutions for a problem like （1） with a parameter if f is monotone increasing.

In the present paper，motivated by[3，7－8]，we consider existence of multiple solutions for the boundary value problemwhere λ＞0 is a parameter and f：R→R is a continuous function.Firstly，by using the Mountain Pass Theorem （cf.[9]），we establish result on the existence of two nonzero solutions of Problem （2） when λ=1.Then，based on a general variational principle of Ricceri，we prove that Problem （2） has infinitely many solution if the nonlinear term f has an suitable oscillation condition.Here we introduce more general conditions on f to guarantee two nonzero the existence of solutions which are different from that on f in[1-2] （see Theorems 1 for more details）.Moreover，unlike in[1]，[3]and[4]，to obtain the existence of infinitely many solutions for Problem （2），we assume that f is neither odd nor monotone （see Theorems 2 and 3 for more details）.

Theorem 1 Assume that the following conditions hold：

（H1）there exist constants θ∈（0，1） and α＞0 such that|f（s）|≤α（1+|s|θ） for all s∈R；

（H2）there exist three positive constants a，b，l withsuch that F（s）≥0 for all s∈（0，b），and F（s）≥ls2for all s∈（a，b）;

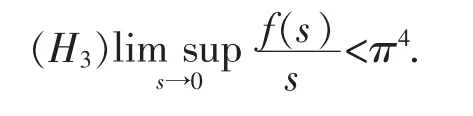
Then，Problem （1） has at least two nontrivial solutions in C4[0，1].

Note that（H3） implies that f（0）=0，then u（x）=0 is a solution of Problem （1），which is called the trivial solution.

Theorem 2 Assume that the following conditions hold：

（H4）F（s）≥0 for all s＞0，and

（H5）there exists a sequence{bn}in （0，∞） withand bn→∞ such that f（s）≤0 for all s∈，bn]，and

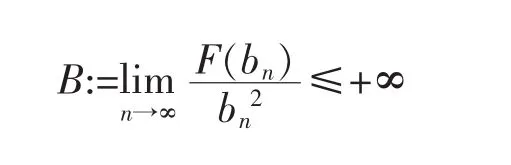
Then

（i）if B＜+∞，for every λ＞π4/（2B），Problem （2） has infinitely many solutions in C4[0，1]；

（ii）if B=+∞，for every λ＞0，Problem （2） has infinitely many solutions in C4[0，1].

Theorem 3 Assume that the following conditions hold：

（H6）F（s）≥0 for all s＞0，and

（H7）there exists a sequence{bn}in （0，∞） withbn+1＜bnand bn→0 such that f（s）≤0 for all s∈，bn]，and

Then

（i）if B＜+∞，for every λ＞π4/B，Problem （2） has infinitely many solutions in C4[0，1]whose norms converge to 0；

（ii）if B=+∞，for every λ＞0，Problem （2） has infinitely many solutions in C4[0，1]whose norms converge to 0.

2 Variational setting

In this section，we will see that Problem （2）has a variational structure.Let C[0，1]denote the usual real Banach space with the norm||u||C=maxx∈[0，1]|u（x）|.By L2[0，1]we denote the real Hilbert space with the inner productand the induced norm

It is well known that to find solutions of Problem （2） in C4[0，1]is equivalent to find solutions of the following integral equation in C[0，1]

where G：[0，1]×[0，1]→[0，1]is the Green function for-u″（x）=0 （x∈[0，1]） subject to u（0）=u（1）=0，i.e.

It is easy to see that G is nonnegative，continuous and max（x，s）∈[0，1]×[0，1]G（x，s）=1/4.

We respectively define operators K：L2[0，1]→C[0，1]and T：C[0，1]→C[0，1]as

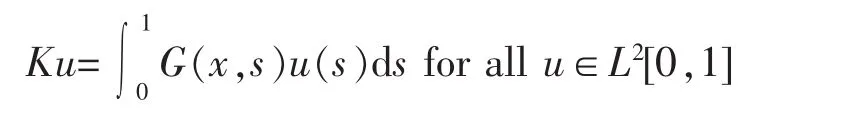
and

Then to find solutions of integral equation （3） in C[0，1]is equivalent to find solutions of operator equation

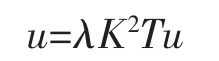
in C[0，1].For the linear operator K，we have the following properties.

Lemma 1 （cf.[3]）

（i）K：L2[0，1]→C[0，1]is a linear completely continuous operator，and K：L2[0，1]→L2[0，1]is also a linear completely continuous operator；

（ii）（Ku，v）=（u，Kv） for all u and v in L2[0，1]；

（iii）the operator equation u=λK2Tu has a solution in C[0，1]if and only if the operator equation v=λKTKv has a solution in L2[0，1].

Remark 1

（a）By the definition of K，we can obtain that Ku≠0 for all u∈L2[0，1]with u≠0.Therefore，Ku1≠Ku2for all u1，u2∈L2[0，1]if u1≠u2.

（b）It is easy to see that the eigenvalues of K2are 1/（n4π4） and the corresponding eigenvectors are sinnπx，n=1，2，…

（c）K2is also linear compact，symmetric and the norm||K2||=1/π4.Moreover，we have||K||=1/π2and

Remark 2 For any u∈L2[0，1]，it follows from the definition K that

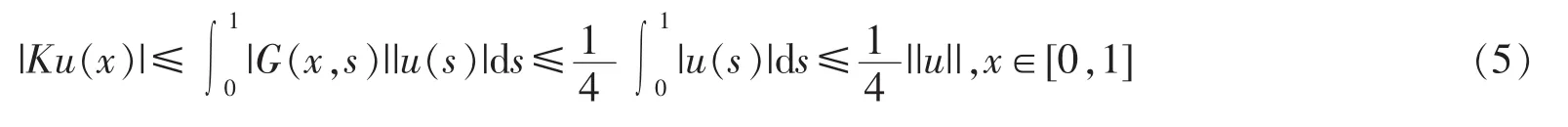
Therefore,

（i）I is Fréchet differentiable on C[0，1]and I′（u）w=（Tu，w）for all u，w∈C[0，1]；

（ii）I◦K is Fréchet differentiable on L2[0，1]and （I◦K）′（v）=KTKv for all v∈L2[0，1].

Let us introduce a functional J：L2[0，1]→R as

Then，according to Lemma 2，J∈C1（L2[0，1]，R） and

It follows from Lemma 1 that Problem （2） has a nontrivial solution in C4[0，1]if and only if the functional J has a nontrivial critical point in L2[0，1].More precisely，if v∈L2[0，1]is a critical point of J，then u=Kv is a solution of Problem （2） in C4[0，1].Thus Problem （2） has a variational structure.

In the end of this section，let us recall the Palais-Smale condition for a functional defined on a Banach space.

Definition 1 Let X be a real Banach space.A functonal J∈C1（X，R） is said to satisfy the Palais-Smale condition （the （PS） condition for short） if any sequence{um}⊂X for which J（um） is bounded and J′（um）→0 as m→∞ possesses a convergent subsequence.

3 Proof of main results

Now we are going to prove our main results.

Proof of Theorem 1 By the preceding section，it is only necessary to prove the functional

has at least two nonzero critical points in L2[0，1].

First of all，we prove that there exists v1∈L2[0，1]such that

By （H1），we obtain

where α′＞0 is a constant.Therefore，by using inequalities （7） and （5），for all v∈L2[0，1]we have

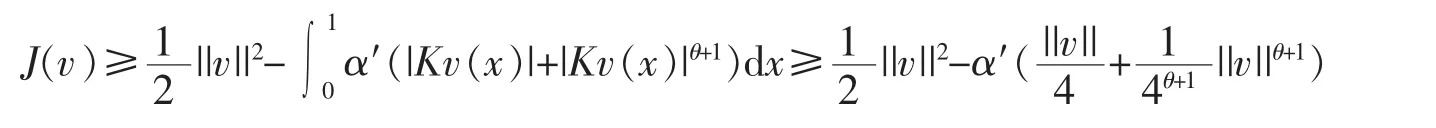
In addition，it follows from Lemma 1 that KTK：L2[0，1]→L2[0，1]is completely continuous，therefore J is a weakly semicontinuous functional on L2[0，1].Then we can find an element v1∈L2[0，1]such that

Secondly，we will prove that J（v1）=infv∈L2[0，1]J（v）＜0.Indeed，chooseand let v0（x）=t0sinπx for all x∈[0，1]，then v0（x）∈（aπ2，bπ2） when x∈（1/4，3/4） and ｜v0｜2=t02/2.Moreover，it follows from Remark 1 that

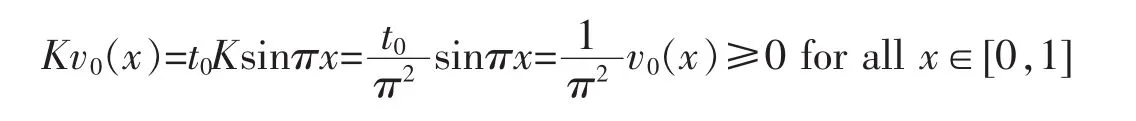
Then，by （H2），we have

From the choice of l，we know J（v1）=infv∈L2[0，1]J（v）≤J（v0）＜0.

Finally，we will use the Mountain Pass Theorem to find the second nonzero critical point of J.For the sake of clarity，we divide the following proof into two steps.

Step 1 We prove that J satisfies the （PS） condition.Let{vn}be a sequence in L2[0，1]such that

We claim that{vn}is bound sequence.In fact，suppose the contrary，then there wound be a subsequence{vni}of{vn}such that||vni||→∞ as i→∞.Since J（v） is coercive，J（vni）→∞ as||vni||→∞ which clearly contradicts the fact that|J（vn）|≤β for all n∈N.Then the properties of K and T guarantee that{vn}has a convergent subsequence.This shows that J satisfies the （PS） condition.

Step 2 We check that the functional J has the Mountain Pass geometry.By （H3），there exists ε∈（0，1）and δ＞0 such that

So

Now we choose ρ＞0 such that ρ＜min{4δ，||v1||}andThen，it follows from （6）,（8） and （4）that for all v∈∂Bρ={v∈L2[0，1]：||v||=ρ},

On the other hand，it is obvious from the choice of ρ that||v1||＞ρ and J（v1）＜0=J（0）.Thus，according to the Mountain Pass Theorem （cf.[9，Theorem 2.2]），there exists v2∈L2[0，1]such that J′（v2）=0 and J（v2）≥η＞0.Since J（v2）＞0＞J（v1），it is clear that v2≠v1.The proof is completed.

In the following，we will prove the existence of infinitely many solutions for Problem （2）.Our main tool is a general variational principle of Ricceri （cf.[10，Theorem 2.5]），which we recall here，stated in the most suitable form for our purposes.

Lemma 3 Let X be a reflexive real Banach space，and let Φ，Ψ：X→R be two sequentially weakly lower semicontinuous and Gâteaux differentiable functionals.Assume also that Φ is strongly continuous and coercive.For every r＞infXΦ，set

Then，the following conclusions holds：

（A）If γ＜+∞，then for every λ∈（0，1/γ），either

（A1）Φ-λΨ possesses a global minimum；or

（A2）there exists a sequence{un}of critical points of the functional Φ-λΨ such that

（B）If δ＜+∞，then for every λ∈（0，1/δ），either

（B1）Φ-λΨ possesses a local minimum which is also a global minimum of Φ；or

（B2）there exists a sequence{un}of pairwise distinct critical points of theweakly converging to a global minimum of Φ.

Proof of Theorem 2 For every v∈L2[0，1]，Φ and Ψ are defined by

thus the energy functional becomes J（v）=Φ（v）-λΨ（v）.Then we only need to prove that Φ（v）-λΨ（v） has infinitely many critical points in L2[0，1].

It is obvious that Φ and Ψ are Gâteaux differentiable and sequentially weakly lower semicontinuous.Obviously，Φ is strong continuous and coercive.

In our case，we can define the function φ of Lemma 3 by putting for every r＞0

We claim that

Clearly， γ≥0.On the other hand，by （H6），we can deduce that there is a sequence{an}in （0，+∞） with an→+∞such that

Let rn=8an2so that rn→+∞.Then for every u∈L2[0，1]with Φ（u）≤rn，we have

Take v0（x）=0 for all x∈[0，1]，then||v0||=0＜2rn，it follows from （10） that

This，together with （9），implies

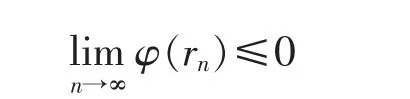
Then γ=0.

In the sequel，we will show that

Indeed，Let wn（x）=π2bnsinπx for all x∈[0，1].Then

Moreover,

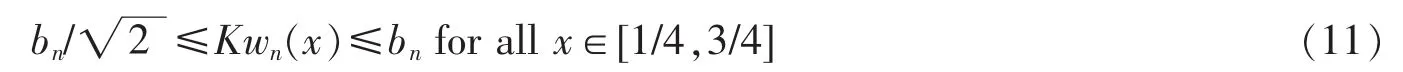
Thanks to （H7），F（s） is nonincreasing for，bn].Thus，according to （H6） and （11），we have

Therefore，for n∈N,

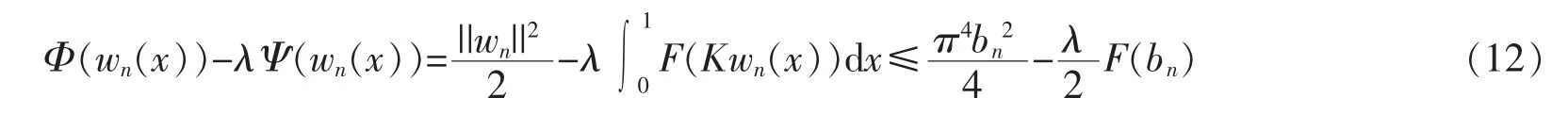
If B＜+∞，let λ＞π4/2B and є∈（π4/2λB，1），then by （H7） there exists Nє∈N such that

for all n＞Nє.Note that the choose of є，it follows from （12） that for all n＞Nє,

Therefore，the （A1）in Lemma 3 can be excluded.Thus，（A2） holds，i.e.there exists a sequence{vn}of critical points of J=Φ-λΨ such that

If B=+∞，let M＞π4/2λ，then by （H7） there exists NM∈N such that

for all n＞NM.This yields that for all n＞NM,

so that

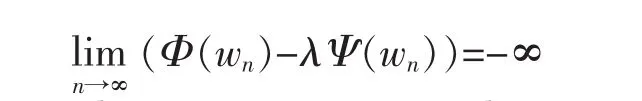
Then，（A2） of Lemma 3 holds for any λ＞0，that is，for every λ＞0 there exists a sequence{vn}of critical points of J=Φ-λΨ such that.This concludes the proof.

Proof of Theorem 3 We take Φ，Ψ and wnas in the proof of Theorem 2.In a similar way we can prove

and for n large enough,

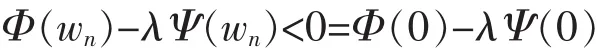
Since||wn||→0 as n→∞，0 is not a local minimum of Φ-λΨ.Therefore，the （B2） of Lemma 3 ensures that there exists a sequence{vn}of critical points of J=Φ-λΨ such thatSo Problem （2） has infinitely many solutions in C4[0，1]whose norms converge to 0.

[1]HAN G，XU Z.Multiple solutions of some nonlinear fourth-order beam equations[J].Nonlinear Anal，2008，68：3646-3656.

[2]HAN G，LI F.Multiple solutions of some fourth-order boundary value problems[J].Nonlinear Anal，2007，66：2591-2603.

[3]LI F，ZHANG Q，LIANG Z.Existence and multiplicity of solutions of a kind of fourth-order boundary value problem[J].Nonlinear Anal，2005，62：803-816.

[4]BAI Z，WANG H.On positive solutions of some nonlinear four-order beam equations[J].J Math Anal Appl，2002，270：357-368.

[5]GRAEF J R，QIAN C，YANG B.Multiple symmetric positive solution of a class of boundary value problem for higher order ordinary differential equations[J].Proc Amer Math Soc，2003，131：577-585.

[6]LIU B.Positive solutions of fourth-order two point boundary value problems[J].Appl Math Comput，2004，148：407-420.

[7]KRISTÁLY A，VARGA C.On a class of quasilinear eigenvalue problem in RN[J].Math Nachr，2005，278（15）：1756-1765.

[8]KRISTÁLY A，MOROSANU G，TERSIAN S.Quasilinear elliptic problem in RNinvolving oscillatory nonlinearities[J].J Differential Equations，2007，235：366-375.

[9]RABINOWITZ P H.Minimax Methods in Critical Point Theory with Applications to Differential Equations[M].Providence：CMBS Regional Conference Series in Mathematics，Amer Math Soc,1986.

[10]RICCERI B.A general variational principal and some of its applications[J].J Comput Appl Math，2000，113：401-410.

一类四阶两点边值问题的多解性

席莉静1，2， 黄毅生2
（1.苏州科技大学 数理学院，江苏 苏州 215009；2.苏州大学 数学科学学院，江苏 苏州 215006）

研究了四阶两点边值问题 u（4）（x）=λf（u（x）），x∈（0，1）；u（0）=u（1）=u″（0）=u″（1）=0 解的存在性，其中λ＞0是参数，f：R→R是连续函数。利用变法的方法和临界点理论，获得了两个非平凡解及无穷多个解存在性的结果。

四阶边值问题；（PS）条件；临界点

2016－10－13

国家自然科学基金资助项目（11471235）；江苏省自然科学基金资助项目（BK20150281）；苏州科技大学自然科学基金资助项目（XKZ201614）；苏州科技大学博士科研启动基金资助项目

席莉静（1971－），女，山西大同人，副教授，博士，研究方向：非线性分析。

O175.8MR（2010） Subject Classification：35J35；35J40；58E05

A

2096－3289（2017）03－0008－07

责任编辑：谢金春