公交车发车频率的博弈分析*

楚彭子 杨京帅 李青霞 高 冲

(长安大学汽车学院1) 西安 710064) (苏州大学东吴商学院2) 苏州 215000)

公交车发车频率的博弈分析*

楚彭子1)杨京帅1)李青霞2)高 冲1)

(长安大学汽车学院1)西安 710064) (苏州大学东吴商学院2)苏州 215000)

为分析公交运营方如何能够高效地满足出行者的乘车需求，基于博弈理论建立公交需求者的乘车博弈模型及公交需求群体与公交运营方的博弈模型，并进行算例分析，分析结果表明，个体公交需求者的时间成本会影响其策略的选择，为保证自身的收益，不同时间成本的需求者会有不同的选乘倾向；针对个体而言，公交运营方策略改变的可能性较小；而对于乘车群体博弈，可以通过改变公交运营方运营成本影响因素中的可控变量，得到最大限度满足公交需求者乘车需求的均衡.

交通工程；公交发车频率；博弈论；纳什均衡；不完全信息

0 引 言

公交车作为大容量载运工具对于缓解城市交通拥堵具有重要意义.公共交通的不同运营措施会直接影响到出行者的公交出行选择，较低的公交满意水平将导致公交需求者的流失与转移.为提升公交运营方的服务质量，国内外学者展开了大量的研究.王佳等[1]通过以公交乘客等车时间、车内拥挤度为上层目标，以公交运营方车辆成本、车辆空载闲置程度为下层目标建立了双层规划模型.卢火平等[2-4]以公交运营方收益和乘客利益最大为目标分别建立了优化模型.许旺土等[5]以社会福利最大为目标，讨论了多时段发车间隔优化随机期望值的问题.董红召等[6-7]在讨论了交通拥堵状态对公交运营的影响后，设计了该交通状态下响应客流需求的发车间隔的计算方法.Robert等[8]认为不同的公交发车间隔会随机地导致不同的候车人数.Savage[9]基于博弈论的视角讨论了一定发车频率下的公交定价问题.

综合看来，当前的研究成果较多采用所获取的乘客数据和优化算法对公交发车频率/间隔进行分析，公交运营方的期望往往关注车辆总空驶时间缩小和利润的增高[10-12]，因而会采用优化车辆排班、最小化驾驶人员的成本等方式来尽可能提高收益[13].随着“以人为本”理念逐渐深入人心，学者们开始更多地考虑出行人的乘车感知和社会福利[14].个体的感知往往会对其行为产生度量，如何让公交运营方在考虑成本的基础上尽可能满足出行者的公交需求是本文运用博弈论研究该问题的基本思路.

1 博弈论与纳什均衡

博弈论的分析过程建立在具有斗争、竞争或合作等事物特征的基础及博弈各方的理性思维之上，该理论能够根据一定的信息对游戏参与方的行为进行预测或利益划分，也可进一步根据预测结果对各参与方的行为进行优化途径的比选研究.博弈开展须具备局中人、行动、策略、规则、支付(又称收益)等要素，该理论已在经济、社会、生物及政治等诸多领域得到广泛应用.

纳什均衡是在博弈过程中的这样的一种理性策略组合，在该策略组合下，每个局中人均不能单方面的改变策略而获得更高的收益，它所表征的策略组合是每个局中人对其他局中人所选策略的最佳反应，即若给定他人策略，局中人均没有足够的理由来打破这种均衡.对于公交车发车频率的问题，公交运营方与公交需求者在策略的选择上构成了博弈，本文基于此寻求该博弈中的纳什均衡.

2 博弈模型的建立

2.1 公交需求者的乘车博弈模型

运用非合作的不完全信息静态博弈对在一定概率分布下的公交车单条运行线路的运营环境及公交需求者的出行条件进行讨论.图1为公交需求者的乘车博弈树.

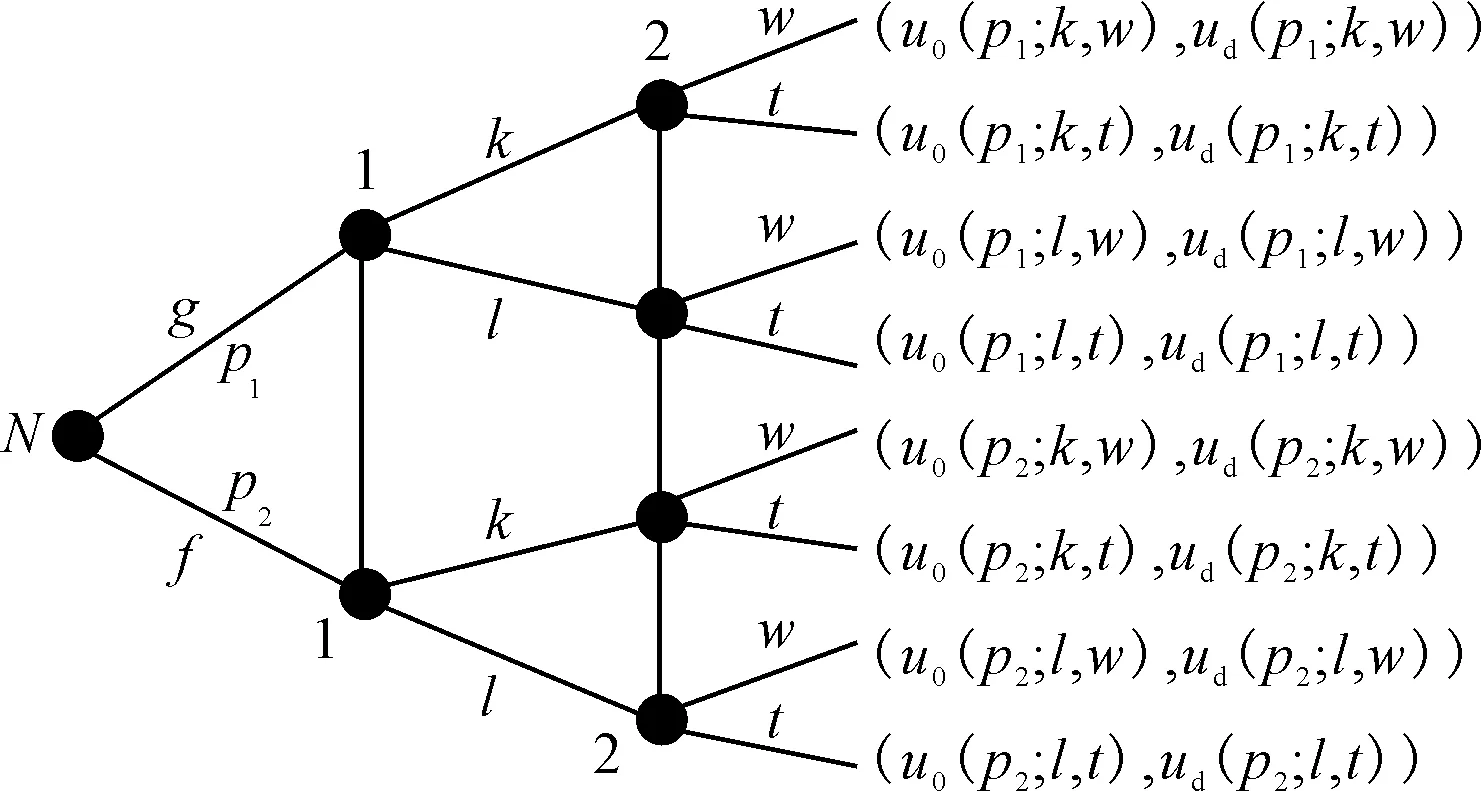
g - 高客流；f - 低客流；p1- 高客流概率；p2- 低客流概率；k - 高频率发车；l - 低频率发车；w - 等待乘坐公交车；t - 非公交出行；ud- 公交需求者的支付方式；u0- 公交运营方的支付方式.图1 公交需求者的乘车博弈树

公交运营收益为其盈利的总和，而影响公交运营收益的因素较多，如发车频率、固定成本、车辆运营时间，以及单位时间运营成本等.其中，发车频率代表公交车单位时间内发车的频率，即单位时间内发车间隔的倒数，当ni计为某天或某时段内公交发车数量时，计算式为

ni=(h×60)/tfi

(1)

式中：i为对公交运营方发车策略的量化形式，取1时代表高频率发车，取2为低频率发车；h为公交运营时段，h；tfi为发车间隔，min/班.

公交需求者在出行时往往会对票价、候车时间及车内时间等进行考量，本文将公交需求者支付定义为不花费任何时间与金钱的预期收益与实际支出之差，由于预期收益的大小难以估量，故将公交需求者的支出取负值作为其支付的计算值.对于该支付，需要考虑到出行费用及出行时间特征的不同来计算.根据客流的影响，面对单个乘车人不同的选择，公交运营方在发车后所获得的收益也不尽相同.两者收益的计算为

(2)

式中：uo(i,j,α)为公交运营方在不同客流及不同发车频率时的收益，j的取值与客流状况相关，取1时代表高客流，2为低客流；α为0-1变量，是公交需求者对公交车选择策略的量化；Rs,Rw,Rej,Rp分别为公交车单车次的公交补贴金额、驾驶员单车次的劳务发放、单车次车辆运行消耗及乘车票价；ud(i,j,α)为不同客流状态下公交运营方不同发车频率所对应的公交需求者收益；β为时间价格系数，表示乘车人对于候车及乘车期间对于时间价值的感知；tpj为不同客流环境下出行者的乘坐公交车时间；ti为不同发车频率下的发车间隔，考虑市区公交车发车频率均较为频繁，将ti/2作为出行者需要等待公交车时间的均值；Rt为选择非公交工具出行所需的费用；ttj为不同客流环境下出行者的非公交出行的时间.

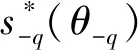
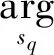
(3)

表1 公交需求者博弈的各方支付

2.2 公交需求群体与公交运营方的博弈

公交需求群体中的个体特征不尽相同，而当前的以互联网技术为载体的智能设备已经使得乘车人可根据智能公交系统及乘车经验，在一定程度上了解到公交车的发车信息和运行信息.为展开群体博弈的分析，本文首先做出以下假设：

①公交的载客能力能够满足乘车需求，即不存在候车后仍需等待下一车次的现象；②路网环境中，非公交出行工具的数量能满足乘车人的即时出行需求；③路网环境中，车头时距仅受发车频率/间隔的影响；④公交需求群体中所存在的对于时间价值感知较高的需求者，在了解发车信息(公交车到站时间)后即选择非公交出行方式.

基于以上假设和上文局中人支付的计算方式，公交需求群体与公交运营方的支付式为

(4)

式中：uo(i,j)和uD(i,j)分别为公交运营方和公交需求群体在不同选择下的收益；N为公交需求者的数量总数；εm为第m个公交需求者对于出行工具的选择，取值为1或0，为对于公交或非公交的选择；βm为第m个公交需求者的时间价格系数；Rit为第m个公交需求者乘坐非公交出行方式的花费；t(m,p,j)及t(m,t,j)为不同客流环境下第m个公交需求者乘坐公交车或非公交的时间.

当面对实际出行状况时，全面的数据采集较为困难，按照抽样或取均值的方法能够较大程度降低计算量.若采用平均值作为代表数据特征的统计量，两者收益的计算方式可以进一步简化为

(5)

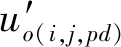
在该博弈中，公交需求群体由两部分组成，即选择公交车和选择非公交车，且群体中个体的选择分布是可以调查的.按照自然所赋予的概率加权后得到的支付，见表2.

表2 公交需求群体博弈的各方支付

实际中，据表2中计算方式可得到某背景下的博弈结果，必要时，可对可控变量进行调整以得到理想的博弈结果.

3 算例分析

本文通过算例对模型进行实证分析.由于在博弈模型中博弈的结果会随着博弈条件的改变而改变，实证分析的数据是多种情况中的其中一种，仅以此为例进行讨论.现有自然、公交运营指标、某公交需求者，以及公交需求群体的特征指标数据，见表3.

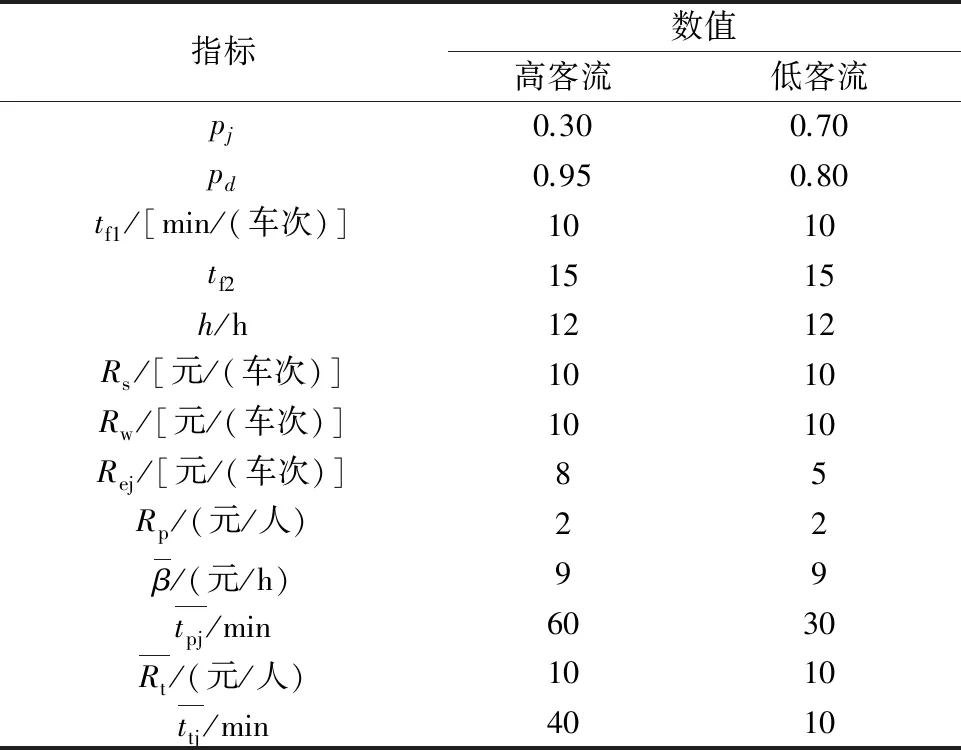
表3 博弈分析算例数据

当算例分析面向时间价值系数β为9元/h的某公交需求者乘车博弈时，根据式(2)及表1所得到的此博弈中局中人支付矩阵见表4.

表4 公交需求者博弈的局中人支付

对于此博弈情形，经采用划线法进行均衡求解的博弈分析认为：对于该公交需求者而言，由于其时间成本较低，其乘坐公交的策略严格占优，即其会选择等待乘坐公交这一策略.但此时，为获得较高利益，公交运营方的最优策略为高客流及低客流时均采用低频率发车.

当另有时间价格系数β为19元/h的某公交需求者，该博弈中局中人的支付矩阵见表5.

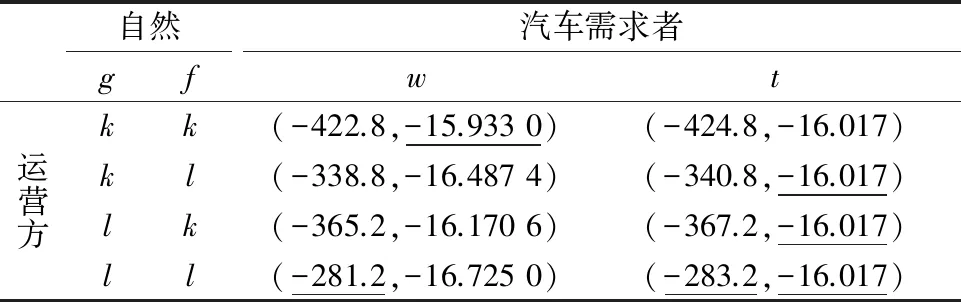
表5 公交运营博弈各方的支付

结果表明，不同时间成本的乘车人会选择不同策略以保证自己的收益.不同发车频率所表现出的候车时间必然会影响到公交需求者的乘车分布，因而基于已知乘车数据的发车间隔优化其效果有待商榷.公交运营方需要依托一定的调查数据来选择、优化和组织不同的发车频率.

针对单个公交需求者讨论的目的在于进一步讨论一定数量的乘车群体.现有该线路计算时段内公交需求者450人，根据式(5)和表2计算得到的局中人所获支付见表6.

表6 公交需求群体博弈的局中人支付

表6中不存在均衡解，即对于公交需求群体而言，当其获得最大支付(-4 286.3)时公交运营方的策略为s(k,k)，但该收益小于公交运营方采取s(l,k)策略和s(l,l)策略时的收益.当面对此种情景，理性的公交运营方会选择收益最大的策略s(l,k).

纳什均衡是一种“双赢”的状态，如何让公交运营方通过策略的改变来满足公交需求群体的收益可基于该思想进行分析.考虑到社会福利，且尽可能满足群体的公交需求和公交运营方的盈利需求，在公共设施供给条件不变的情况下，可采用提高发车频率来吸引更多公交需求者的乘车、适当增加公交补贴及降低运营费用等多种方式以使得公交运营方能够在高客流及低客流时均采用高频率发车，且收益为最大值.根据式(3)及博弈“均衡”内涵，对于该公交运营方，则u(s(k,k))∈max {u(s(k,k))，u(s(l,k))，u(s(k,l))，u(s(l,l))}，即博弈的最优策略.对此，本文以增加公交补贴为例，经联立方程并求解，得到Rs≥12.375，即为促使本文算例中公交运营方的选择策略为在高客流及低客流时均采取高频率发车[10 min/(车次)]，可将公交补贴这项指标调整为不小于12.375元/车次.

4 结 论

1) 单个公交需求者的不同特征会影响其乘车博弈的结果，在一定的乘车环境下，对于高时间成本的需求者，其倾向于采取非公交的出行方式以保证自己的收益，低时间成本需求者则会倾向于乘坐公交.公交运营方则会采取自身收益最大时的发车策略，即针对个体而言，其策略改变的可能性较小.

2) 对于乘车群体，公交运营方的策略选择及公交需求者的博弈可能存在不理想的均衡，也可能不存在均衡，通过改变公交运营方运营收益中的可控变量可得到能够最大程度满足公交需求者乘车需求的均衡.公交运营方在优化发车间隔时不仅要考虑当前客流，同时也要注重潜在客流.

3) 本文在计算各方支付时选取的指标并不是十分全面，并基于一定的假设，实际计算时需要根据需求对运营时间段和分析指标进行选择和细化，以求更为精确的结果.

[1]王佳,胡列格,贺翔.城市公交发车频率优化的双层规划模型及算法[J].系统工程,2013,31(12):69-73.

[2]卢火平,韩印,姚佼,等.基于博弈的公交线路发车间隔优化模型研究[J].交通与运输,2012,8(2):52-56.

[3]刘芹.差分进化细菌觅食算法求解公交车调度问题[J].交通运输系统工程与信息,2012,12(2):156-161.

[4]戴连贵,刘正东.公交调度发车间隔多目标组合优化模型[J].交通运输系统工程与信息,2007,7(4):43-46.

[5]许旺土,何世伟,宋瑞,等.多时段公交发车间隔优化的随机期望值模型[J].北京理工大学学报,2009,29(8):676-680.

[6]董红召,孔娟娟,刘晴辉.交通拥堵条件下的公交发车间隔过渡模型研究[J].交通运输系统工程与信息,2016,16(3):101-106.

[7]王超,徐猛.考虑道路交通拥堵的公交发车间隔优化模型[J].交通运输系统工程与信息,2011,11(4):166-172.

[8]ROBERT S T,李志强.公交车发车间隔与排队长度的研究[J].北京化工大学学报(自然科学版),2010,37(3):131-133.

[9]SAVAGE I. The dynamics of fare and frequency choice in urban transit[J]. Transportation Research Part A,2010,44(10):815-829.

[10]刘志刚,申金升.区域公交时刻表及车辆调度双层规划模型[J].系统工程理论与实践,2007,27(11):135-141.

[11]魏金丽,郭亚娟,张萌萌.基于集合覆盖理论的公交线路驾驶员排班优化方法[J].公路交通科技,2016,33(1):125-129.

[12]ULUSOY Y Y, CHIEN S I. Optimal bus service patterns and frequencies considering transfer demand elasticity with genetic algorithm[J]. Transportation Planning and Technology,2015,38(4)：409-424.

[13]QU H Z, CHIEN S I, LIU X B, et al. Optimizing bus services with variable directional and temporal demand using genetic algorithm[J]. Journal of Central South University,2016,23(7):1786-1798.

[14]杨熙宇,暨育雄,张红军.基于感知的公交调度发车频率和车型优化模型[J].同济大学学报(自然科学版),2015,43(11):1684-1688.

欢 迎 订 阅

《武汉理工大学学报(交通科学与工程版)》

《武汉理工大学学报(交通科学与工程版)》是交通运输领域高水平的学术理论性刊物，是我国交通运输领域学术交流的园地，体现综合交通格局,繁荣大交通科技研究，促进交通运输科技成果转化，为交通运输工程一级学科建设服务，为发现和培养交通运输领域科技人才服务，为促进我国交通运输学术研究与国际交流服务.

本刊突出现代交通科学与工程，兼顾其他相关学科及交叉学科.主要刊登有关船舶与海洋工程、机械科学与工程、船舶机械、轮机工程、港口机械、智能交通系统(ITS) 、车辆工程 、铁路运输工程、汽车工程、载运工具、内燃机工程、航空工程、信息科学与技术、计算机、自动控制、测量与控制技术、通信导航与电子系统、移动通信、电气工程、航运技术、交通土木建筑工程、资源与环境工程、材料科学与工程、物流工程、交通管理科学与工程等学科领域的学术论文及科研成果.

刊号：CN 42-1824/U 国际标准刊号：ISSN 2095-3844

本刊邮发代号：38-148 定价：20.00元/期，120.00元/年

欢迎广大读者到全国各地邮局订阅。

武汉理工大学学报(交通科学与工程版)

Game Analysis of Bus Departure Frequency

CHU Pengzi1)YANG Jingshuai1)LI Qingxia2)GAO Chong1)

(SchoolofAutomobile,Chang’anUniversity,Xi’an710064,China)1)(SchoolofBusiness,SoochowUniversity,Suzhou215000,China)2)

In order to analyze how the bus operator could satisfy the demands efficiently for passengers, the ride game of the bus demander and the game between bus demanders and an operator are established based on Game Theory. By analyzing a numerical example, the results showe that: the traveler’s time-cost of the individual will affect his choice of the strategy to ensure his own benefits; the traveler’s different time-value will determine people’s tendency of choice. As an individual, the possibility of change choice of the public transport operator is small. But for travels groups, the balance of maximally meeting the demand of travelers taking the public transit will be achieved by changing the influence factor of the controllable variables in game.

traffic engineering; bus departure frequency; game theory; Nash equilibrium; incomplete information

2017-06-09

*国家自然科学基金项目资助(51108040)

U491.1

10.3963/j.issn.2095-3844.2017.04.035

楚彭子(1989—)：男，硕士生，主要研究领域为交通运输规划与管理、道路交通安全