孤立波数值造波研究*
2017-09-11姚建喜吴静萍
姚建喜 吴静萍
(高性能船舶技术教育部重点实验室1) 武汉 430063) (内河航运技术湖北省重点实验室2) 武汉 430063) (武汉理工大学交通学院3) 武汉 430063)
孤立波数值造波研究*
姚建喜1,2,3)吴静萍1,2,3)
(高性能船舶技术教育部重点实验室1)武汉 430063) (内河航运技术湖北省重点实验室2)武汉 430063) (武汉理工大学交通学院3)武汉 430063)
基于开源平台OpenFOAM研究开发一种可模拟推板运动的动边界条件,实现推板造波数值模拟.以孤立波为研究对象,基于Goring孤立波造波理论以及Fenton九阶孤立波解,确定两种推板运动形式,并据此对孤立波造波和传播过程进行模拟.数值模拟结果表明,基于Goring方法所得到的孤立波后方水面凹陷现象较基于Fenton方法所得到的孤立波后方水面凹陷现象更为显著,且波高衰减更快.将数值模拟结果与水槽试验结果进行比较,对两者之间的差别进行分析和讨论.
孤立波;OpenFOAM;推板造波;数值造波;水槽试验
0 引 言
近年来,海啸频发且近岸建筑物增多,研究海浪在近岸水域中的传播机理和特性是预防灾难、减少损失的一个重要途径.孤立波是一种浅水域有限振幅波,与海浪的传播特性相似,因此通常以孤立波的研究结果来分析近岸的海浪.自1844年罗素在实验室中发现孤立波以来,人们对孤立波理论进行了大量研究,其中如何在实验室中通过人工方式产生孤立波是研究其传播特性的一个重要方面.
文献[1-3]对实验室造孤立波的方法多有报道,其中Goring方法应用较为广泛.该方法是基于一阶孤立波解的推板造波理论,适合波高较小的孤立波,当波高较大时,产生的孤立波后方会出现水面凹陷现象,且在传播过程中波高发生衰减.Wu等[4]基于高阶孤立波解对Goring方法进行了改进,获得的波形得到明显改善.
通过近30年的发展,数值计算方法逐渐成熟且已经成功地应用于造波及波浪传播过程的数值模拟研究,出现了所谓的“数值波浪水池”概念,数值计算方法的应用更有利于观察水波现象,是当前研究波浪传播特性的重要手段之一.本文基于开源计算流体动力学平台OpenFOAM研究开发一种动边界条件,使之能模拟推板线运动,从而实现数值造波.根据Goring孤立波造波理论和Fenton九阶孤立波解,确定两种推板运动形式,对孤立波的造波及其传播过程进行数值模拟[5-10].将计算结果与水槽试验结果进行比对以验证数值模拟的有效性.
1 孤立波推板造波理论
图1为推板造波示意图.对于给定水深h,当推板以速度u沿水平方向运动时,水面即兴起波浪.推板运动速度是时间t或推板位置ξ的函数.根据相关造波理论,当推板的运动速度函数或位置函数确定后,便可驱动推板作相应运动,获得目标波形.

图1 推板造波示意图
根据Goring孤立波造波理论,推板位置和速度的关系为
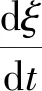
(1)
式中:c为波速;η为波面抬高且
η=Hs2
(2)
其中:H为目标波高;s=sech [k(ξ-ct)].k和c的表达式为
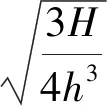
(3)
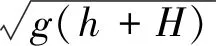
(4)
当水深和目标波高确定后,将式(2)代入式(1)并采用数值方法进行求解可获得推板位置的时历曲线.上述方法中的推板位置是根据一阶孤立波解而得到的.
本文的研究同时采用Fenton推导的九阶孤立波解来确定推板位置时历曲线.η,k和c的九阶解分别为
(5)
(6)
(7)
表1为式(5)~(7)中的系数ηi,ki和ci或其计算表达式. 将式(5)代入式(1),便可求解得到基于九阶孤立波解的推板位置时历曲线,求解算法可参考文献[4],这里不再赘述.

表1 九阶孤立波解的系数
2 数值造波方法
本研究通过求解纳维-斯托克斯(Navier-Stokes,N-S)方程来模拟推板运动,实现数值造波.这里仅考虑二维情况,在图1的坐标系0-xz下对流体动力学控制方程进行描述.基于不可压缩假设,流体连续性方程为
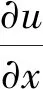
(8)
N-S方程为
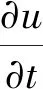

(9)
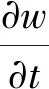

(10)
式中:u和w为流体速度分量;ν为粘性系数;p为动压;ρ为密度;g为重力加速度.采用流体体积分数法(volume of fluids,VoF)来捕捉自由面,体积分数控制方程为
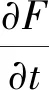
(1)
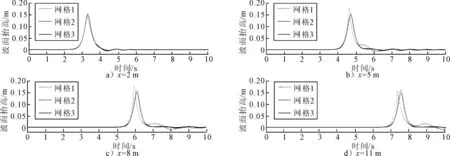
式中:F为流体体积分数,若F=1为计算单元充满水,若F=0为计算单元充满空气,若0 式(9)和(10)中的粘性系数和密度为 ρ=Fρw+(1-F)ρe (12) ν=Fνw+(1-F)νe (13) 式中:ρw和νw为水的密度和粘性系数;ρe和νe为空气的密度和粘性系数. 本文推板数值造波是在开源CFD平台OpenFOAM上进行的. OpenFOAM提供了基于有限体积方法的求解器以及多种方程离散格式.尽管OpenFOAM自带基于网格变形方法的动网格功能模块,但该求解器尚不能用于模拟给定的推板运动.因此,本研究在OpenFOAM的基础上植入新的动边界条件,实现推板数值造波.新开发的边界条件,可直接从文件中读取推板位置时间历程,数值模拟时推板按照文件中给定的位置时间历程作线运动.对于给定的水深和目标波高,首先根据前述的Goring或Fenton方法确定推板位置时间历程,并保存在一个文件中,然后将它作为求解器的输入进行数值造波模拟. 数值模拟时,建立的二维虚拟波浪水池尺寸为:0 m 因为计算区域是一个长方形,所以数值模拟更适合采用结构化网格,图2为计算网格的局部视图,图中灰色代表水,白色代表空气,图中水面处于初始时的静止状态.整个计算区域由四个边界组成,边界条件的设置情况为:①在水池两端(x=0 m和x=18 m)和水底(z=-0.3 m)边界上设置壁面边界条件;②在水池顶端(z=0.3 m)边界上设置空气入口边界条件. 图2 计算网格局部视图 数值模拟时,将水池一端壁面边界看成是推板,初始时处于x=0 m的位置,并使之按给定的方式运动进行数值造波. 为保证模拟精度,首先研究分析波形对网格疏密程度和时间步长的依赖性,这里仅考虑基于Fenton方法得到的波形.为此,生成三个疏密程度不同的结构化网格,网格1、网格2和网格3.这三个网格分别由300×10,600×20和1 200×40个计算单元组成,且沿水池长度和高度方向是等间距的. 对于网格依赖性分析,数值模拟的时间步长为0.001 s.图3为在孤立波传播方向上不同位置时的波面抬高时历曲线. 图3 网格依赖性分析 由图3可知,在同一位置,随着网格加密波面抬高峰值和其出现时间的差异变小;采用三个网格计算得到的波面抬高峰值出现时间之间的差异随离推板初始位置的距离而逐渐变大,例如,在x=2 m位置时,三条曲线峰值出现时间较接近,而在x=11 m位置时差异较大;使用网格3计算得到的波面抬高峰值与目标波高非常接近,表明网格3的密度能保证数值模拟精度. 对于时间步长依赖性分析,数值模拟时采用网格3,且时间步长分别为0.001,0.002和0.004 s值模拟结果见图4.由图4可知,时间步长对波面抬高峰值有较大影响,时间步长越大孤立波在传播过程中衰减越快. 图4 时间步长依赖性分析 基于以上网格和时间步长依赖性分析,发现使用网格3和时间步长0.001 s时的数值模拟结果已经达到足够精度. 首先根据Goring方法确定前文计算工况时的推板运动时间历程,并将时间历程作为求解器的输入进行造波数值模拟.数值模拟时使用网格3,时间步长取为0.001 s. 图5将基于Goring和Fenton方法得到的在孤立波传播方向上不同位置时的波面抬高时历曲线进行了比较.采用两种方法得到的波面抬高的一个主要差别在于孤立波传播过程中Goring方法得到的波形后方水面凹陷更为显著.值得注意的是在x=11 m时基于Fenton方法得到的波形后方水面凹陷现象已经不明显.另一方面,由图5可知,Goring方法得到的波高随时间的推移衰减更快,导致波速变得更慢. 图5 比较基于Goring和Fenton方法的计算结果 图6将基于Goring和Fenton方法得到的在x=1.55 m和x=3.95 m位置时的波面抬高时历曲线与试验曲线进行了比较.水槽试验是在流体力学实验室完成的,水槽尺寸为18 m×0.6 m×0.8 m. 由图6可知,计算结果与试验结果表现出良好的一致性,但与计算曲线相比,试验曲线的峰值都较小,且在孤立波后方出现了更剧烈的水面凹陷和振荡现象.计算结果和试验结果之间的差异估计由以下原因造成: 图6 比较计算结果和试验结果 1) 数值造波仅考虑二维情况,忽略了水槽侧壁的影响,这可能是导致波高发生衰减的原因之一. 2) 数值模拟时,将虚拟水池的一端作为推板,而水槽试验中的推板是独立于水槽壁面的,且推板与水槽侧壁和水底存在间隙,尽管间隙很小,但试验时仍然观察到水从间隙中溅出.数值模拟引入的简化估计是导致计算结果和试验结果之间差异的主要原因. 1) 数值模拟得到的波高与目标波高非常接近,且试验结果和计算结果的比较表明,数值模拟是有效的. 2) 与Goring方法相比,采用Fenton方法得到的孤立波波高衰减及其后方水面凹陷现象得到改善. 3) 计算结果与试验结果之间的差异估计由数值模拟时引入的简化造成,后续研究工作可考虑真实工况以进一步验证本文方法的精度. [1]HSIAO S C, LIN T C. Tsunami-like solitary waves impinging and overtopping an impermeable seawall: experiment and RANS modeling [J].Coastal Engineering, 2010,57:759-774. [2]CHEN Y Y, YANG J H. An experimental study of steep solitary wave reflection at a vertical wall [J].European Journal of Mechanics B/Fluids, 2015,49:20-28. [3]CHEN Y S, YEH H. Laboratory experimental on counter-propagating collisions of solitary waves[J]. Journal of Fluid Mechanics, 2014(7):577-596. [4]WU N J, HSIAO S C. The study on solitary waves generated by a piston-type wave maker[J]. Ocean Engineering, 2016(11):114-129. [5]FENTON J. A ninth-order solution for the solitary wave [J].Journal of Fluid Mechanics,1972,53(2):257-271. [6]李邦华,郑向远,李伟,等.波浪水槽中S to kes五阶波的数值生成[J].武汉理工大学学报(交通科学与工程版),2016,40(2):238-244,250. [7]张莉,郭海燕,李效民.南海内孤立波作用下顶张力立管极值响应研究[J].振动与冲击,2013(10):858-865. [8]关晖,魏岗,杜辉.内孤立波与潜艇相互作用的水动力学特性[J].解放军理工大学学报(自然科学版),2012(5):478-486. [9]徐鑫哲.内波生成机理及二维内波数值水槽模型研究[D].哈尔滨:哈尔滨工程大学,2012. [10]王飞.内孤立波作用下小尺度竖直圆柱体的水动力特性研究[D].青岛:中国海洋大学,2012. A Study on Numerical Generation of Solitary Wave YAO Jianxi1,2,3)WU Jingping1,2,3) (HubeiKeyLaboratoryofInlandShippingTechnology,Wuhan430063,China)2)(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)3) To realize the simulation of wave generations by a piston-type wave maker, a dynamic boundary condition is developed to simulate the motion of a paddle based on the open source platform OpenFOAM. Taking the solitary wave as an example, two types of motion which are derived from the Goring’s theory for generation of solitary wave and the Fenton’s ninth order solution of solitary wave are determined. Based on that, the generations of solitary wave and its propagation are studied. The numerical results show that the depression of the free surface behind the Goring-based solitary wave is more significant than that behind the Fenton-based wave and the Goring-based wave height decays more quickly. solitary wave; OpenFOAM; piston-type wave maker; numerical wave generation; flume experiment 2017-05-22 *国家自然科学基金项目(51609188,51609187,51609186)、内河航运技术湖北省重点实验室基金项目(NHHY201502)、中央高校基本科研业务费专项资金(2016IVB007,2017IVB006)资助 U675.91 10.3963/j.issn.2095-3844.2017.04.014 姚建喜(1985—):男,博士,讲师,主要研究领域为船舶与海洋结构物水动力性能3 计算条件,网格和边界条件

4 网格和时间步长依赖性分析
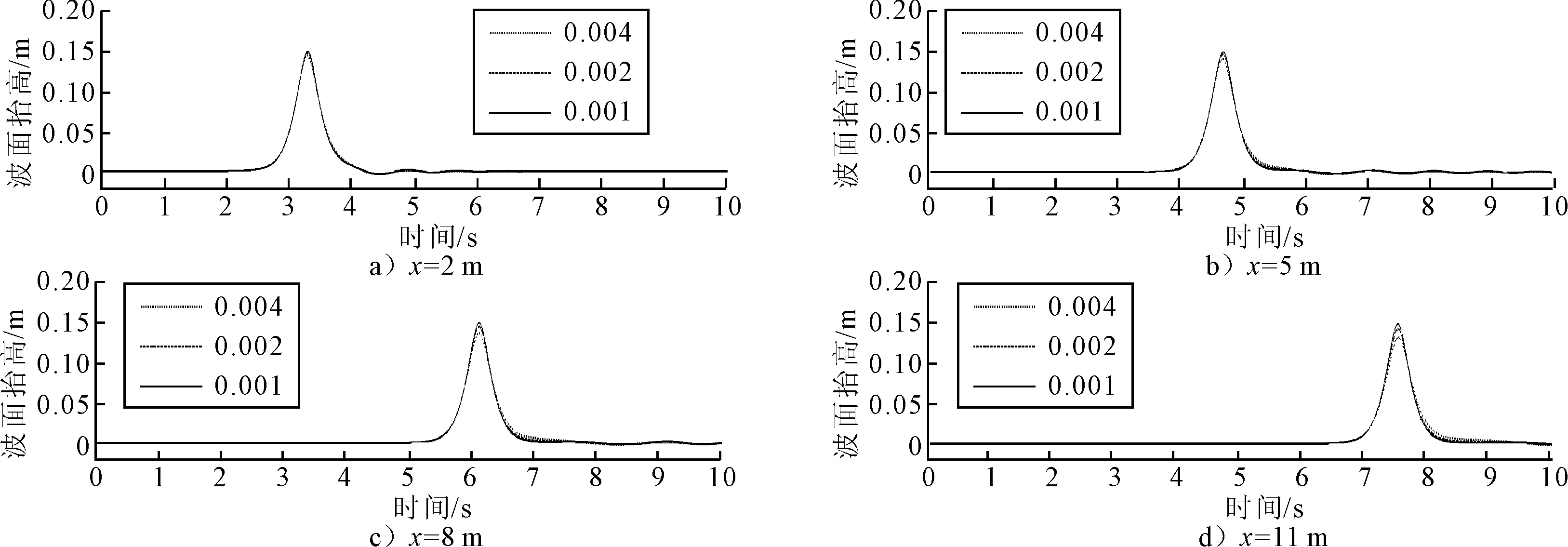
5 数值结果分析和验证
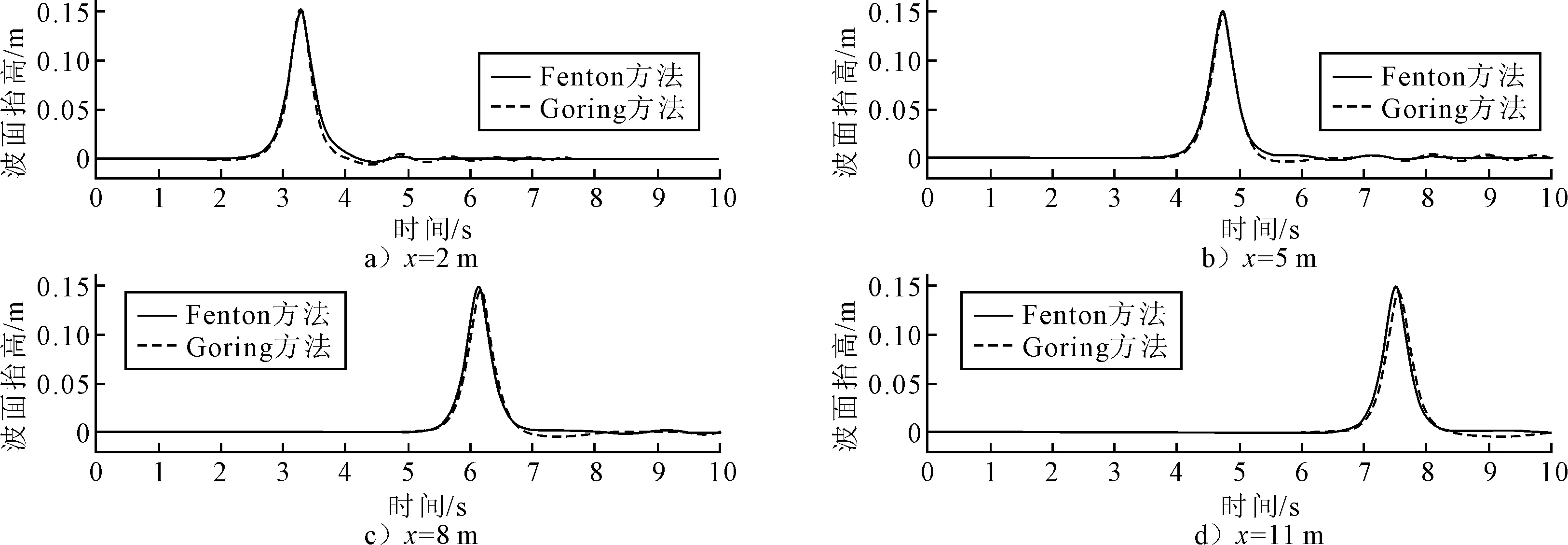
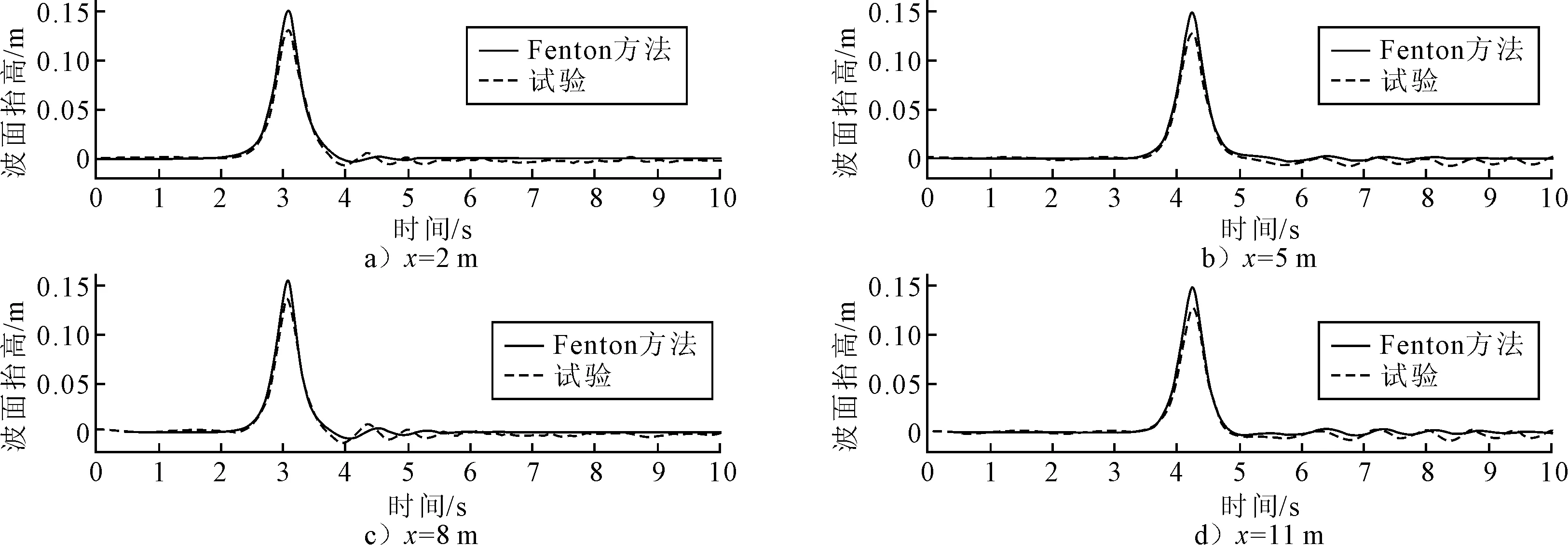
6 结 论
(KeyLaboratoryofHighPerformanceShipTechnologyofMinistryofEducation,Wuhan430063,China)1)
