钢桁梁柔性拱吊装阶段风致效应分析*

邓雅思 张谢东 封仁博 张朦朦 张倍阳

(武汉理工大学交通学院1) 武汉 430063) (中交一公局第五工程有限公司2) 北京 100024)

钢桁梁柔性拱吊装阶段风致效应分析*

邓雅思1)张谢东1)封仁博2)张朦朦1)张倍阳1)

(武汉理工大学交通学院1)武汉 430063) (中交一公局第五工程有限公司2)北京 100024)

为探究强风作用下大跨钢桁梁柔性拱在吊装过程中的结构响应，基于振动分析理论推导出结构随施工阶段变化的频率、刚度及质量增长率的关系，并结合钢桁梁柔性拱实例，通过MATLAB脉动风数值模拟与MIDAS/Civil施工阶段仿真计算，分析了柔性拱架设阶段体系的动力特性及风致效应.计算结果表明，脉动风数值模拟与功率谱吻合度较高；增长率关系式能较好反应出结构刚度变化；在柔性拱架设过程中，结构的横向刚度变化显著，并呈现出先减小后增大的趋势，最小值出现在最高拱肋的后续节段.

桥梁工程；风致效应；时程分析；钢桁梁柔性拱；施工阶段

0 引 言

在强风地区建设大跨度钢桁梁柔性拱桥，风荷载是重点考虑因素，尤其在柔性拱架设阶段，由于拱圈尚未合龙，此时的拱圈相当于由多根吊杆弹性支撑的曲梁，结构体系刚度小、变形大，风致振动响应也会更大[1]，在风荷载作用下的受力非常不利.目前，钢桁梁桥在架设过程中的施工计算通常只考虑了风的静力作用而忽略了脉动风引发的抖振力效应[2].然而，长吊杆支撑的拱肋在动风荷载下产生的结构振动不仅会降低合龙精度，破坏桥梁结构的合理内力状态，还会导致施工人员产生强烈的眩晕感从而影响施工的安全性[3].因此，柔性拱架设阶段的风致效应分析对结构的顺利施工具有重要意义.

1 风致效应分析理论

作用于桥梁结构上的风荷载由平均风作用、脉动风的背景作用及结构惯性动力作用叠加而成.由文献[1]可知，风的静力荷载可采用考虑了平均风和脉动风背景响应的静阵风荷载来计算，钢桁梁桥主要考虑横向风荷载的阻力作用，其计算公式参考规范较为简单.桥梁振动是由脉动风引起的强迫力和结构自身运动引起的自激力共同作用下产生的.当风速值较低时，自激力表现为正阻尼，结构振动主要由强迫力所控制，这时振动表现为抖振[4].桥梁施工阶段中的抖振响应分析往往成为控制大跨度桥梁设计、施工的关键因素.抖振分析方法分为时域法和频域法.近年来在风工程领域中，考虑到气动力的非线性及大跨度柔性体系的几何非线性等影响因素，越来越多的学者倾向于采用时域法进行桥梁的抖振研究[5].

1.1 时域抖振分析理论

采用有限元软件进行桥梁结构振动分析的实质是解有限自由度系统的振动方程：

(1)

根据目标功率谱函数模拟空间脉动风场比较常用的方法有线性滤波法和谐波合成法.对于模拟出的水平和竖向风速，按照Scanlan的准定常气动力理论，风阻力的抖振力时程[7]表达式为

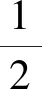
(2)

式(1)的求解通常采用的算法有线性加速度法、Wilson-θ法、Runge-kutta法及Newmark-β法等，钢桁梁桥线性时域分析通常采用Newmark-β法计算，结构阻尼采用瑞利阻尼.

1.2 动力特性分析

风致效应计算需分析结构的动力特性，即对结构振动频率、振型等参数的分析.根据多自由度体系无阻尼自由振动的特征方程及刚度矩阵与质量矩阵的正交性，可得结构r阶固有频率ωr与刚度Kr、质量Mr的关系[8]如下式为

(3)

为分析柔性拱架设各阶段相关参数变化的关系，现推导同属r阶的两不同阶段r1，r2各参数关系.

由式(3)可得

ωr1=K1/2r1·M-1/2r1(r1=1,2,…,N)

(4)

ωr2=K1/2r2·M-1/2r2(r2=1,2,…,N)

(5)

定义质量增长率δM、刚度增长率δK、频率增长率δω为

(6)

(7)

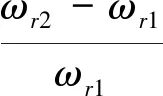
(8)

由式(6)～(7)求解出Mr2和Kr2，带入式(8)得

ωr2=(1+δK)1/2(1+δM)-1/2ωr1

(9)

δK=(δω+1)2(1+δM)-100%

(10)

由式(10)可知，根据结构的频率增长率和质量增长率可以求得结构的刚度增长率，进而可用于结构刚度变化的分析.

2 钢桁梁柔性拱实例分析

2.1 工程背景

某三跨连续钢桁柔性拱桥，跨径布置为120m+228m+120m.主桁采用有竖杆N形三角桁式，平行桁高15m，节间长12m和13m.柔性拱肋按圆曲线布置，矢高69m，矢跨228m，矢跨比为1/3.3.桥型布置及节点编号见图1.该桥采用钢桁主梁和柔性拱相结合的结构形式，主桁采用“吊索塔架+悬臂施工”对称施工实现跨中合龙，柔性拱从北岸向南岸安装，最后在拱肋A12′G13′与上弦杆A12′对接口处实现合拢.大桥桥位区基本风压700Pa，常年多遇强风，因此，强风作用下结构在架设过程中的效应分析对柔性拱顺利合龙具有重要意义.

图1 桥型布置图(尺寸单位：m)

2.2 脉动风的数值模拟

本文基于MATLAB软件，采用线性滤波法进行桥址处的脉动风速时程模拟.水平和竖向的脉动风谱分别采用Kaimal谱和Panofsky谱，根据结构特点随机风场模拟了21个点(拱肋17个，主桁4个)，频率区间为(0.01～10)，步长0.01；施工风速取桥址百年一遇的基本风速进行折减，为27.4m/s，B类地貌，粗糙度取为0.03，模拟时间间隔0.1s，样本时间204.8s.图2列出了拱肋G13点横风向风速时程曲线及模拟谱与目标谱的比较.由图2可知，模拟谱与目标谱吻合度较高，说明脉动风模拟结果比较合理.

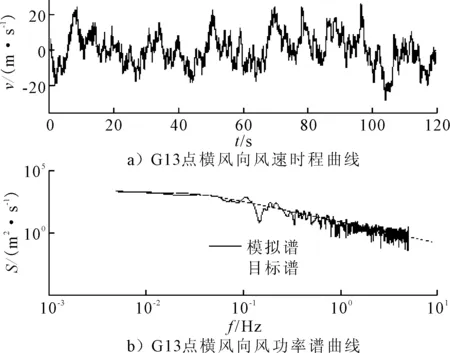
图2 水平脉动风速时程与比较

2.3 有限元建模

采用桥梁结构有限元分析软件MIDAS/Civil对柔性拱架设阶段进行施工阶段模拟及风致响应分析.模型采用常用的右手坐标系建立，以北岸固定支座位置为原点，X轴正向沿顺桥向指向南岸，Y轴正向沿横桥向指向下游，Z轴正向沿竖直向上.柔性拱架设的模拟计算中共建立14个施工阶段，图3为柔性拱G19节段架设完成.

静阵风荷载响应分析采用规范[1]中的公式计算.其中，主桁上下弦及拱肋的横桥向风载采用主

图3 拱架设至G19阶段模型图

2.4 施工阶段动力特性分析

通过对拱吊装阶段进行特征值分析可知，结构前两阶振型均为一阶竖弯和一阶横弯.柔性拱架设各施工阶段系统的自振频率与振型见表1.结构首次出现横弯和竖弯的振动频率对比见图4.

表1 各施工阶段自振频率与振型

图4 架设节段首次横弯/竖弯的频率变化

由表1可知，随着柔性拱节段的架设，结构一阶振动频率先减小后增大，在G15′阶段架设处降至最低0.601.此外，结构一阶振动形式在G19节段安装时从竖弯变化为横弯.对照图4，基于结构质量变化一致，而竖向振动频率相对于横向降低更缓慢，这说明拱节段的架设对结构横向刚度的削弱大于竖向刚度.提取并分析各阶段模型质量与基频，由式(9)计算得刚度增长率，三者的变化见图5.

图5 增长率随拱架设阶段的变化

由图5可知，刚度增长率在节段G13至G15′的架设过程中为负数，这说明结构刚度在此阶段随架设节段的安装而逐渐降低，并于架设G15′节段时下降至最小；刚度降幅度显著的施工阶段为架设G19～G15′节段，此阶段时结构的一阶振型为横弯，因此结构的横向刚度在该阶段急剧下降，施工时需重点关注；节段G14′～G13′架设中，结构的横向刚度呈现出显著的增长，这主要是因为短吊杆加强了主梁与拱肋约束的缘故.

动力特性分析结果表明，柔性拱架设的G19～G15′节段结构横向刚度下降明显，横向振动基频在G19～G13′架设阶段较低.在施工过程中，结构在横向风荷载作用下有较大可能产生大偏移及应力过大现象，因此有必要对施工关键阶段进行抗风分析.

2.5 风致效应分析

2.5.1 静阵风效应

经计算，在静阵风荷载作用下结构吊杆的最大压应力、平联的最大拉应力及主桁的最大拉应力均出现在G13′架设阶段，主桁最大压应力出现在G14′架设阶段，为横向最大偏移出现在G15′架设阶段，具体计算结果见表2.

2.5.2 时域抖振响应及分析

1) 响应对比分析 为便于比较，将无风作用、抖振惯性力作用以及静阵风作用下结构内力及位移的最大响应列于表2.

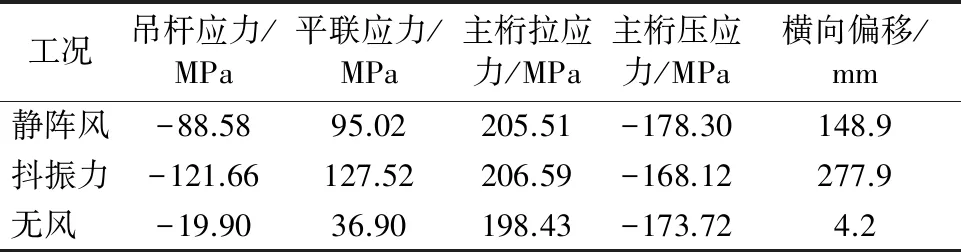
表2 结构的最大响应对比

由表2可知：

①通过对静阵风和抖振力作用下的响应极值与无风荷载下的响应极值进行比较可知，风荷载主要对柔性拱的杆件产生影响，对于钢桁主梁杆件的应力影响较小，一方面说明钢桁主梁横向刚度较大，柔性拱则相对较弱，另一方面反映出主桁的应力主要是由结构自重、边跨压重等施工荷载控制，受风荷载的影响很小.但由于主桁杆件的应力在无风荷载时就已较大，再叠加动风和静风的综合作用，杆件应力将超过材料容许应力，不满足施工要求.

②在风荷载作用下，柔性拱结构的静力与动力响应最值在相同施工阶段的相同单元或节点取得，但动力响应大于静力响应，横向偏移差别较为显著，动风下横向偏移放大系数约为2.因此当以横向位移进行施工控制时，只考虑静阵风作用的计算结果会较为保守.此外，该桥在静阵风作用下拱肋节点横向偏移达14 cm，不满足规范[9]要求，施工时需采取一定的控制措施.

③风荷载作用下，吊装G15′节段时拱肋节点的横向位移取得最大值，吊装G13′节段时各杆件应力取得最大值，施工中应对安装G15′节段拱肋节点的横向位移及13′节段的杆件应力重点控制.

2) 抖振分析 目前，抗风规范并未对抖振响应的取值做出明确规定，现行的抗震规范中常取位移和加速度的响应进行比较[10]，其中选取加速度响应是由于惯性力对结构体系的作用于地震作用效果相当，施工阶段亦可根据结构加速度响应值分析人体对荷载的适应性.分析结果见图6，其中横向位移时程响应峰值出现在G15′节段的安装阶段(图6a)).对于加速度时程，考虑到风速达到六级时便会停止施工，为更加合理地对加速度响应进行判断，此处选取5级上限风速10.7 m/s进行模拟，然后进行抖振分析.取安装G15′节段时跨中E19点的横向加速度响应时程如图(b)所示，其竖向与顺桥向加速度响应均较小.研究表明，人体能够接受是最大侧向加速度[11]为0.2 m/s2，在图6b)的时程曲线中，加速度低于0.2 m/s2的置信度达到99.2%，可以认为在该风速下，桥面的操作人员相对安全；但拱肋节点的横向加速度响应高达1.8 m/s2，远超过人体能接受的加速度上限，因此不建议进行柔性拱的吊装与相关操作.

图6 相关响应的时程曲线图

3 结 论

1) 结构的横向刚度变化显著，并随施工节段的架设呈现出先减小后增大的趋势，最小值出现在最高拱肋的后续节段.

2) 风荷载下主桁杆件已超过杆件容许应力，拱肋横向偏移超过规范允许值，建议采取相应控制措施；此外，当采用横向位移进行施工控制时，只考虑静阵风作用的计算结果会较为保守.

3) 结构在5级大风作用下，跨中桥面点最大横向加速度可为人体所接受，但不宜进行柔性拱的吊装及相关操作.

4) 结构横向刚度较小，故静风荷载与抖振惯性力只考虑了横桥向的风阻力作用，升力、扭矩及相关效应的组合是否会对结构产生更大影响有待进一步分析.

[1]中交公路规划设计院.公路桥梁抗风设计规范：JTG/T D60-01-2004[S].北京：人民交通出版社，2004.

[2]徐宏，杨敏，王庆，等.风荷载对连续钢桁梁悬拼施工影响的仿真分析[J].桥梁，2009(28)：64-67．

[3]崔飞.大跨度拱桥施工阶段的风致响应及抗风研究[D].武汉：武汉理工大学，2013．

[4]LIN Y K, ARIAEATNAM S T. Stability of bridge motion in turbulent winds[J]. Stuct mech，1980，8(1)：1-15．

[5]陈政清．桥梁风工程[M].北京：人民交通出版社，2005.

[6]刘智芳．强风地区大跨度钢桁拱桥施工控制关键技术研究[D].广州：华南理工大学，2014.

[7]张谢东，黄伟文．转体施工大悬臂T构的抗风性能研究[J].武汉理工大学学报(交通科学与工程版)，2015，39(1)：9-11．

[8]李东旭．高等结构动力学[M].2版.北京：科学出版社，2010.

[9]中铁三局集团有限公司．铁路桥涵工程施工质量验收标准[M].北京：中国铁道出版社，2004.

[10]中华人民共和国住房和城乡建设部.建筑抗震设计规范：GB 50011-2010[S].北京：人民交通出版社，2010.

[11]徐宏，郭敏.连续钢桁梁悬拼施工中人体对振动的适应性研究[J].桥隧施工与机械，2015，77(4)：77-80.

Wind Effect Analysis of Steel Truss Girder with Flexible Arch During Hoisting Stage

DENG Yasi1)ZHANG Xiedong1)FENG Renbo2)ZHANG Mengmeng1)ZHANG Beiyang1)

(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)1)(TheFifthEngineeringCo.Ltd.ofFirstHighwayEngineeringCompanyofChinaCommunicationConstructionCo.Ltd.,Beijing100024,China)2)

In order to explore the structural response of steel truss girder with flexible arch under the extreme wind action in the process of hoisting, based on the theory of vibration analysis, the relationship of the structure’s frequency increment, stiffness increment and mass increment with the change of construction is deduced. Through numerical simulation of fluctuating wind by MATLAB and construction stage simulation calculation by MIDAS/Civil, the dynamic characteristics and wind-induced response during flexible arch hoisting stage are analyzed systematically with an engineering example. The calculation result shows that the numerical simulation of fluctuating wind is in good agreement with power spectrum; the relational expression of growth rate can reflect the change of structural stiffness efficiently. During the hoisting stage of flexible arch, the lateral stiffness of structure changes significantly, it decreases first and then increases, the minimum lateral stiffness occurs after the highest arch rib section.

bridge engineering; wind effect; time history analysis; steel truss girder with flexible arch; construction stage

2017-06-10

U448.22

10.3963/j.issn.2095-3844.2017.04.031

邓雅思(1993—)：女，硕士生，主要研究领域为桥梁结构分析与施工控制