需求信息不对称下数据交易拍卖定价机制研究

郭鑫鑫, 李倩茹, 王海燕, 杜建国

(1.江苏大学 管理学院,江苏 镇江 212013; 2.江苏科技大学 经济管理学院,江苏 镇江 212100; 3.东南大学 经济管理学院,江苏 南京 211189)

0 引言

伴随着机器学习和数据挖掘技术等迅速发展,数据已成为数字经济时代重要的生产要素和战略资产[1]。然而,数据产品的定价受多种主客观因素影响,呈现出价值多样性、不确定性等特征,难以按照传统商品的方式进行定价[2]。从数据卖方角度,同一数据产品可以多次出售,使其不能按照交易价格等于边际成本进行定价;从数据买方角度,数据产品只有在使用后才能明确其真实的价值,具有一定的价值滞后性[3]。面对数据产品定价过程中缺乏历史经验数据进行借鉴,探究数据产品交易定价机制成为推动数据交易平台可持续发展的关键[4,5]。

从实际数据交易场景出发,参与数据产品交易双方(即数据交易平台和潜在数据需求者)往往存在着需求信息不对称。一方面,数据交易平台不能准确预测数据需求者的期望交易价格、购买能力及风险偏好等信息,倾向设计较高的交易价格来销售数据产品;另一方面,数据需求者不能事前准确获知被交易数据产品的质量、完整性和真实性等信息,倾向选择以不超过对其估值的价格来购买数据产品[6]。众所周知,数据交易双方追求自身收益最大化,均不会主动披露自身对数据产品的认知信息。此外,数据需求者对数据产品的期望效用也存在不同认知,致使对数据产品呈现出差异化的需求[7,8]。

当前,相关学者已从不同的视角出发对数据交易定价进行了研究。BIMPIKIS等[9]研究了垄断市场环境下数据使用者之间的竞争如何影响数据经纪商的最优销售策略。RAY等[10]在数据交易过程中引入样品展示来缓解双方间信息不对称,通过构建数据交易协商式定价模型,探讨经纪商是否应该以及如何进行样品展示。喻海飞和黄晋婷[11]研究了闭环数据供应链下的数据产品定价策略问题,分别构建了集中定价、分散定价和收益共享三种不同的数据定价模型。马滔等[12]构建了数据披露与数据交易两阶段博弈模型,探究数据拥有者的价格披露与数据经纪商交易价格间交互关系。此外,拍卖定价方法也被部分学者应用于数据产品交易定价中。通过梳理相关文献发现,学者们采用的拍卖模型涉及维克里拍卖、VCG拍卖、反向拍卖和双向拍卖等类型。在数据交易过程中,具体选择何种拍卖机制需要综合考量买卖双方的相对市场力量,是否有中介机构充当拍卖商及设定的定价原则等因素。张小伟等[13]对采用博弈论和拍卖研究方法的相关文献进行了综述,比较了两种研究方法下的不同数据定价模型及模型的优劣势。

上述文献为本文设计数据产品交易拍卖定价机制奠定了研究基础,但尚未发现相关文献针对数据交易价格和交易量联合决策问题开展探究。基于机制设计理论和多物品最优拍卖设计原理[14],本文以排他性强的数据产品为研究对象,探究数据交易平台与数据需求者进行数据所有权交易,通过设计拍卖机制来确定最优的数据产品交易价格及相应的交易数量。

1 模型假设和问题描述

1.1 模型假设

根据实际的交易场景,考虑数据交易市场中存在一个数据交易平台和众多潜在数据需求者。每位数据需求者依据数据产品价格大小决策数据购买量,故整个数据交易过程呈现“一对多”的博弈关系。为方便后文的问题描述和模型分析进行如下假设。

1)假设市场上数据需求者的数量为n,即i=1,2,…,n,这些数据需求者构成的集合为N={1,2,…,n}。数据交易平台向数据需求者设定的初始交易价格为p,相应的数据需求者i=1,2,…,n的数据需求量为xi≥0,i∈N,xi=0,其中,i=1,2,…,n表示数据需求者选择放弃购买。

3)依据数据交易平台的历史成本信息,定义c(·)为数据交易平台对数据产品进行脱敏、清洗及格式化等处理的成本函数,并且是关于数据量xi,i∈N连续单调递增可微的凸函数[15]。

4)定义ki为数据需求者i=1,2,…,n的最大数据需求量,D是数据交易平台可供给的总数据量。为保证优化问题存在最优解,假设D与ki满足如下关系:

基于前面的相关符号定义,可以获知数据需求者i=1,2,…,n从平台上购买数据产品时,其获得的收益为

vi(xi)=φi(xi)-pxi

(1)

考虑到数据需求者追求自身收益最大化,将依据平台设定的交易价格决策数据购买量,故数据需求者面临的决策问题为

(2)

(3)

同理,基于上文给出相关符号定义,数据交易平台的收益函数可表示为

(4)

1.2 问题描述

本文聚焦于数据交易平台与数据需求者进行数据所有权交易,即部分数据产品被交易给某位需求者后,无法再交易给其他需求者,呈现出排他性。因此,在数据供给量固定的情况下,数据交易平台倾向于设计较高的价格,以实现平台收益最大化。然而,当平台设定较高的交易价格时,数据需求者对数据产品的偏好降低,进而影响数据产品的需求量[16]。考虑到数据交易平台与数据需求者间存在利益冲突及数据需求者相互之间的竞争关系,数据交易平台需要设计一个公平合理的交易价格,通过对数据交易量合理分配,使得在满足数据需求者的需求时,实现平台自身收益最大化,即实现数据交易系统社会福利最大化。根据数据交易系统的社会福利为数据交易平台收益及所有数据需求者的收益之和,可得

(5)

进一步,数据交易平台面临的决策问题可表示为

(6)

显然,数据交易平台与数据需求者间存在需求信息不对称,导致平台不能获知φi(·)的具体表达式,进而无法对所构建的优化问题(6)进行求解,换句话说,优化问题(6)是一个NP-hard问题。

基于最优化理论,数据交易平台要获得优化问题(6)的最优解,需要数据需求者主动共享自身的效用函数信息。然而,考虑数据需求者的自私性,往往会策略性地共享自身的效用函数信息,以追求自身收益的最大化。因此,要解决这种信息不对称下的优化问题,本文利用机制设计理论和拍卖理论来设计一种数据交易拍卖定价机制,引导数据需求者提交真实的效用函数信息,进而决策出最优的数据产品交易价格及相应的交易量。

2 机制设计环境描述与目标设定

2.1 数据交易定价机制环境描述

假设数据需求者对数据产品的偏好为θi,i∈N,其代表着数据需求者的类型[17]。定义数据需求者向数据交易平台进行投标策略为si:Θi→Si,其中,Θi是数据需求者i=1,2,…,n的类型空间,Si为基于数据需求者类型的策略空间。每位数据需求者通过要向平台进行投标,以揭示自身的偏好信息。在获得数据需求者的投标后,数据交易平台可以计算出最优的数据产品交易价格和交易量,即结果函数g(·)。因此,数据交易平台要设计的拍卖定价机制为M=(S1,S2,…,Sn,g(·)),其中包含信息空间S=S1×S2×…×Sn和结果函数g=S1×S2×…×Sn→X×P。该结果函数可将数据需求者的投标策略映射为具体的交易结果,即g(S)=(x1,…,xn,p)。

2.2 数据交易定价机制目标设定

假设数据需求者相互独立且具有不完全信息,投标过程中采用的是贝叶斯博弈。在选择投标策略时,每位数据需求者始终选择能够最大化自身收益的投标策略,并且不考虑其他数据需求者的行动策略。因此,本文采用占优策略均衡来描述数据需求者间的博弈均衡结果。

3 数据交易拍卖定价机制设计

3.1 模型处理

借鉴相关文献中提出的研究方法,本文对优化问题(6)中的约束条件进行放松,将不完全信息下的Stackelberg博弈问题转化成资源分配问题,即

(7)

显然,在优化问题(7)中,数据交易平台的决策变量转变为数据需求者的交易数量xi,i∈N。因此,本文将优化问题(7)看作数据交易平台与数据需求者进行合作来实现数据交易系统社会福利最大化。显然,优化问题(7)的最优解是优化问题(6)最优解的上界。换句话说,通过优化问题(7)实现的数据交易系统社会福利往往大于通过优化问题(6)实现的数据交易系统社会福利。此外,由于c(·)是连续递增可微的凸函数,而φi(·)是连续递增可微的凹函数,使得优化问题(7)的最优解可以通过设定恰当的数据交易价格来实现,表明通过优化问题(7)获得的最优解是紧凑的。因此,通过数据交易拍卖定价机制M=(S1,…,Sn,g(·))获得的数据交易分配结果只需满足优化问题(7)即可。

3.2 设计数据交易拍卖定价机制

由数据需求者效用函数(2)关于xi进行一阶求导,可得

(8)

同时,将优化问题(6)关于数据交易价格p应用KKT条件,可得,

(9)

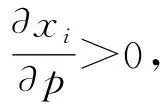
(10)

进一步,整合公式(8)和公式(10),可得

(11)

命题1数据交易平台的拍卖定价机制为M*=(S1,…,Sn,g(·)),信息空间Si是关于数据交易价格p连续单调递减的函数空间,结果函数g(·)为

g(s1(·,θ1),…,sn(·,θn))=(s1(p*,θ1),…,sn(p*,θn),p*)

(12)

其中,p*是数据产品最优交易价格且满足

(13)

(14)

(15)

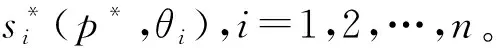
4 算例实验

通过一个算例来验证所设计的数据交易拍卖定价机制的有效性和合理性。借鉴采用需求函数进行投标的相关文献,将数据需求者向数据交易平台提交的投标策略设为

si(p,θi)=ki-pθi,∀i=1,2,…,n

(16)

显然,该投标策略表示数据需求者i=1,2,…,n的最大数据需求量为ki,i∈N;伴随着数据交易价格p越高,数据需求者对数据产品的需求量越少;反之,数据需求者对数据产品的需求量越多,符合现实中的数据产品交易场景。

根据前文的设定,si(p,θi)满足

si(p,θi)≥0

(17)

进一步,经过计算可知数据需求者的偏好θi的取值范围为

(18)

另外,数据需求者i=1,2,…,n的收益函数可表示为

ui(p,θi)=φi(si(p,θi))-p×si(p,θi)

(19)

因此,数据需求者i=1,2,…,n面临的决策问题为

(20)

为了便于下文计算,本文设定数据产品供给总量是固定的而非弹性变化,故数据交易系统社会福利最大化等价于最大化所有数据需求者的效用,即

(21)

根据前文设计的数据交易拍卖定价机制,数据交易平台按照数据需求者提交的需求函数对数据产品交易量进行分配。因此,要实现数据交易市场出清,需要满足

(22)

经过计算可得,数据产品最优交易价格为

(23)

综上,数据交易平台可以设定最优数据交易价格为(23),分配给数据需求者i=1,2,…,n的交易量为si(p*,θi)。

5 结束语

从信息不对称角度出发,数据交易平台无法获知数据需求者的效用函数信息,进而无法设定最优的数据交易价格及合理分配数据交易量。本文聚焦于数据交易平台与数据需求者进行数据所有权交易,利用机制设计理论和拍卖理论,将数据交易定价问题映射为机制设计问题。通过对数据交易平台与数据需求者间交易行为分析,设计了数据产品交易拍卖定价机制,其中信息空间是关于数据交易价格连续单调递减的函数空间,结果函数是由数据需求者提交的需求函数决定。所设计的数据交易拍卖定价机制可激励数据需求者投标真实的需求函数信息,满足拍卖理论中的激励兼容和个体理性。从实践应用角度,本文提出的研究方法可有效地解决需求信息不完全下的数据产品交易定价问题,减少数据交易平台与数据需求者的讨价还价行为,为数据交易平台设计公平的交易价格及合理分配数据交易量提供了理论与实践指导。

本文研究过程中仍存在一些不足如尚未对提供撮合服务的数据交易平台的定价机制进行分析、探究排他性较弱的数据产品的定价机制等。学者们未来可以进一步挖掘数据交易定价与交易量分配联合决策问题,开展更深入和更广泛的研究,以期完善本文所提出的拍卖定价机制。