小区开放对道路通行的影响

林宇浩+吴毓双+刘闯

摘要：随着城市交通网络压力的日益增大，研究开放中国传统的封闭式小区对于道路交通的影响具有现实意义。文章从信号灯处排队等待时间这个因素来考虑。根据排队论的思想建立了等待制模型，分析了开放小区对于其周边道路交通状况的影响。

关键词：交通流；排队论；小区开放

一、研究背景

随着城市交通网络压力的日益增大，如何缓解道路交通的压力成了亟待解决的问题。由于开放小区能否缓解道路交通的压力，优化道路网结构，提高道路通行能力等问题都不得而知，虽然理论上来说小区开放后，路网密度提高，道路面积增加，通行能力自然会有提升，但有人对这一提议也提出了质疑，认为这与小区面积、位置、外部及内部道路状况等诸多因素有关，不能一概而论。还有人认为小区开放后，虽然可通行道路增多了，相应地，小区周边主路上進出小区的交叉路口的车辆也会增多，也可能会影响主路的通行速度。

二、模型的建立和求解

（一）具体的问题背景与车流量规定

1. 问题假定

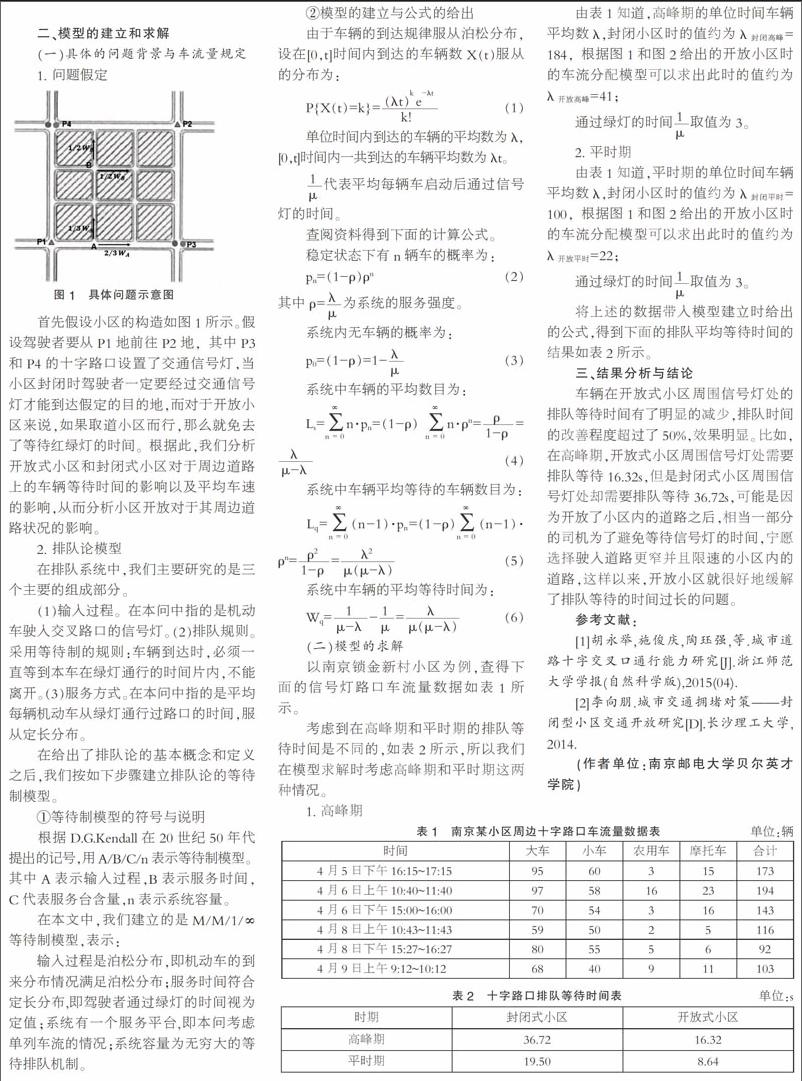
首先假设小区的构造如图1所示。假设驾驶者要从P1地前往P2地，其中P3和P4的十字路口设置了交通信号灯，当小区封闭时驾驶者一定要经过交通信号灯才能到达假定的目的地，而对于开放小区来说，如果取道小区而行，那么就免去了等待红绿灯的时间。根据此，我们分析开放式小区和封闭式小区对于周边道路上的车辆等待时间的影响以及平均车速的影响，从而分析小区开放对于其周边道路状况的影响。

2. 排队论模型

在排队系统中，我们主要研究的是三个主要的组成部分。

（1）输入过程。在本问中指的是机动车驶入交叉路口的信号灯。（2）排队规则。采用等待制的规则：车辆到达时，必须一直等到本车在绿灯通行的时间片内，不能离开。（3）服务方式。在本问中指的是平均每辆机动车从绿灯通行过路口的时间，服从定长分布。

在给出了排队论的基本概念和定义之后，我们按如下步骤建立排队论的等待制模型。

根据D.G.Kendall在20世纪50年代提出的记号，用A/B/C/n表示等待制模型。

其中A表示输入过程，B表示服务时间，C代表服务台含量，n表示系统容量。

在本文中，我们建立的是M/M/1/∞等待制模型，表示：

输入过程是泊松分布，即机动车的到来分布情况满足泊松分布；服务时间符合定长分布，即驾驶者通过绿灯的时间视为定值；系统有一个服务平台，即本问考虑单列车流的情况；系统容量为无穷大的等待排队机制。

由于车辆的到达规律服从泊松分布，设在[0，t]时间内到达的车辆数X（t）服从的分布为：

将上述的数据带入模型建立时给出的公式，得到下面的排队平均等待时间的结果如表2所示。

三、结果分析与结论

车辆在开放式小区周围信号灯处的排队等待时间有了明显的减少，排队时间的改善程度超过了50%，效果明显。比如，在高峰期，开放式小区周围信号灯处需要排队等待16.32s，但是封闭式小区周围信号灯处却需要排队等待36.72s，可能是因为开放了小区内的道路之后，相当一部分的司机为了避免等待信号灯的时间，宁愿选择驶入道路更窄并且限速的小区内的道路，这样以来，开放小区就很好地缓解了排队等待的时间过长的问题。

参考文献：

[1]胡永举，施俊庆，陶珏强，等.城市道路十字交叉口通行能力研究[J].浙江师范大学学报（自然科学版），2015（04）.

[2]李向朋.城市交通拥堵对策——封闭型小区交通开放研究[D].长沙理工大学，2014.

（作者单位：南京邮电大学贝尔英才学院）endprint