基于排队论模型分析交通事故对城市道路通行能力的影响

付南南

摘要：本文以交通事故中的占用车道为例进行研究，采用数据拟合和排队论的思想分析得到了实际通行能力以及事故中车辆排队长度与通行能力、事故持续时间、上游车流量间的关系，从而得出车道被占用对城市道路通行能力的影响。为解决日常生活中道路被占用而导致交通拥堵问题提出了建设性的意见。

关键词：实际通行能力；数据拟合；排队论；交通事故

道路通行能力也称道路容量，是道路的一种性能，能度量道路疏导车辆的能力。随着我国社会经济的持续快速发展，城市已成为经济增长的重要地区，机动车也随之迅猛增多。道路上发生的交通事故、路边停车、占道施工等行为使车道被占用而导致道路横断面通行能力在单位时间内降低，若是不能及时得到解决，则会导致交通堵塞，影响人们的正常生活。合理的分析道路被占用的各个因素及其联系，建立起相关模型，可以尽可能的解决道路被占用所带来的困扰。我们以交通事故这一典型事例为代表，观察分析视频中两次交通事故，研究了车辆被占用对对城市道路通行能力的影响，颇具代表性和合理性，这将为日后解决道路被占用而导致交通拥堵问题产生重大影响。以下是相关的实证分析。

一、事故所处横断面的实际通行能力

1.假设在理想的道路和交通条件下，当具有标准长度和技术指标的车辆，以前后两车最小车头间隔连续行驶时，单位时间内通过道路上指定断面的最大车辆数，记作N（辆/h）。

2.车道宽度对路段通行能力的影响：道路的通行能力C是车道宽度b的函数。车道的宽度达不到要求必然影响车速，车速的降低则意味着通行能力的减小。车道宽度对道路的通行能力和行车的舒适影响很大：从保证通行能力的角度考虑，必需的车道宽度b=3.50m。当车道宽度b大于3.50m时，不影响通行能力；当b小于3.50m时，则车速下降，通行能力减小；车道宽为3.25m时，通行能力修正系数a车道为0.94；车道宽为3.00m时，通行能力修正系数a车道为0.85；车道宽为2.75m时，通行能力修正系数a车道为0.77。

3.多车道对路段通行能力的影响：在一些城市主干道上，同一行驶方向的车道往往不止一条，在多车道的情况下，同向行驶的车辆由于超车、绕越、停车等原因影响另一条车道的通行能力。一般越靠近路中心线的车道，其影响越小，因此在无分隔带的同向车道上，靠近路中心线的车道通行能力为最大：靠近侧石的车道，其通行能力为最小，其影响用修正系数a条来表示。据观测，自路中心线起第一条车道的修正系数a规定为1.00，其余车道的修正系数依次为：第二条车道为0.80-0.89；第三条车道为0.65-0.78；第四条车道为0.50-0.65；第五条车道为0.40-0.52.为了统一数据，我们在本论文中第一车道a条采用数值1，第三车道a条采用数值0.72。

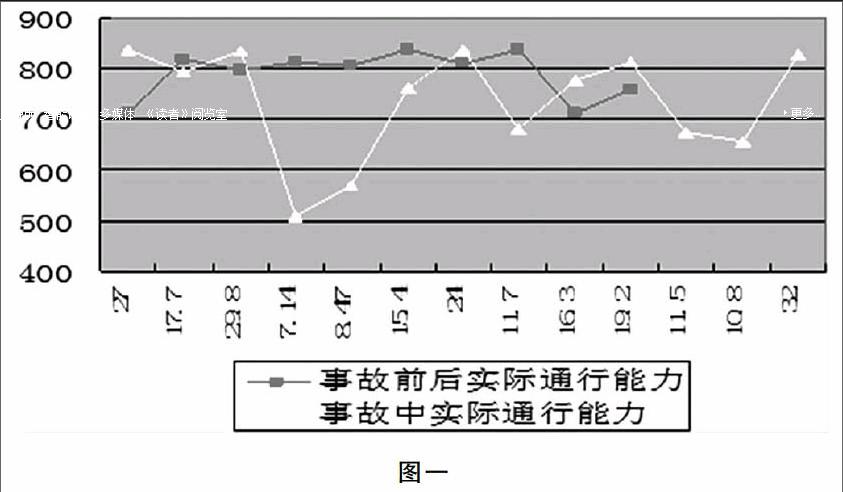
通过对图一中两折线图的对比，我们可以清晰得出事故从发生到撤离期间事故所处横断面的实际通行能力的变化趋势：在最开始的一小段时间内由于刚开始车辆较少，通行能力变化不大，但已有车辆开始滞留，过了一段时间之后由于上游路段绿色信号灯的作用，车辆的不断驶来，较多的车辆连续不断往事故处拥挤，使得此处的通行能力急剧下降，之后随着时间的推移，再加上上游信号灯固定的时间变化，事故处的实际通行能力开始回升，最后趋于相对平稳的范围内波动。

二、横断面车道三的实际通行能力.

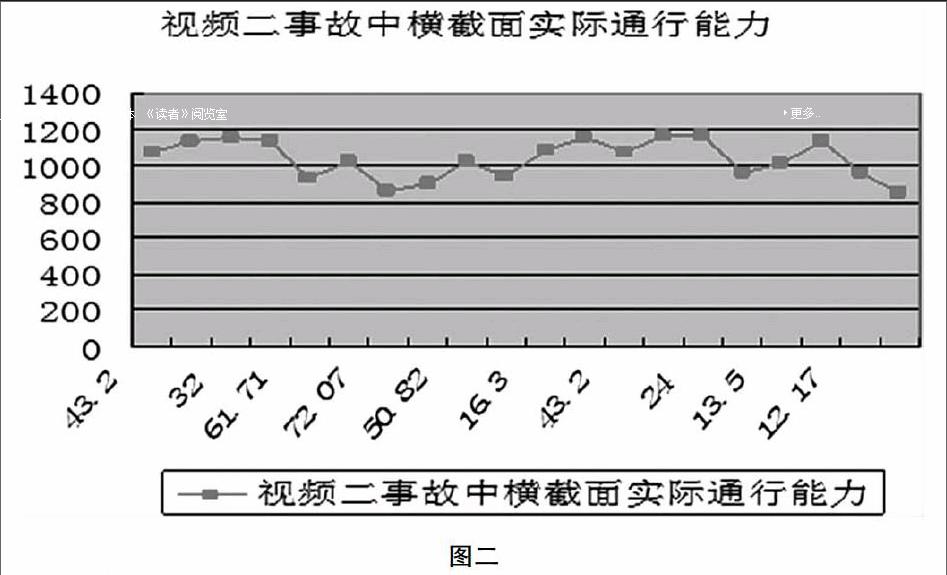
折线图可以看出由于视频一与视频二所占车道不同，因而虽然是同一横断面，实际通行能力仍然存在着差异，这是由于在视频一中，车祸将直行车道、左转车道堵住，车辆只能从右转车道通过。而堵住的两个车道的流量比例占79%，处在这两个车道的车必须插入右转车道才能行使通过，由于被堵车道车多所以插入右转车道时间会比较长，故车祸发生后道路通行能力马上下降.道路通行能力减小到约为原来的三分之一，随着上游不断进来的车，事故发生点开始堵车，道路通行能力为实际通行能力，一直处于波动阶段，车祸撤离后恢复至原来的道路通行能力.在视频二中车祸发生点在右转车道与直行道处，直行、右转车道的车需要插入左转车道，由于左转车道的流量比例为35%，比右转车道高出很多，所以开始出现了不堵车的情况；当越来越多的车插入右转车道后才使得其通行能力下降使得道路被堵，直到车祸撤离后才缓解堵车现状，恢复到以前的道路通行能力。

三、实际通行能力和上游车流量与时间函数关系式的建立

我们假设道路发生事故的排队系统服从排队论中的成批到达的MkM1排队模型。这种模型是指上游车辆到达事故处为最简单流，即由于上游信号灯的影响，车辆到达事故处的时间间隔是服从负指数分布的排队系统。

为确定每批车辆到达的时间间隔和等待时间分布的方法，一般是按照统计学方法，用理论分布去拟合实测资料并估计其参数值。本问题用到的输入过程和理论分布分别是泊松流和负指数分布。

1.该系统的输入过程{M（t），t≥0}为Poisson流，平均到达速率为λ（单位时间内的到达次数，λ>0），但每隔一段时间到来的不是一辆车，而是一批车，设本问题中每批到达k辆车，车的数量为∞；

2.对于每辆车在此路段的停留时间{vn，n=1，2，…}相互独立并且都服从负指数分布，通过速率μ；

3.系统容量为有限值x，当有车辆到达该路段的时候，若该路段的通行能力正常，则该车辆可以正常通过，而当此处发生交通事故时，道路的实际通行能力下降，此时若有一批车辆从上游驶过来，则这些到达的车辆要在队列中排队等待行驶通过.

我们设N（t）表示t时刻系统的排队长度，由于系统容量为有限值，故N（t）的可能取值空间为I={0，1，2，…，x}，N（t）的取值空间就是状态空间，系统可在这些状态之间变化，相邻状态就是相差不大于1的车辆数.系统中下一时刻车辆的数目只可能增加一个、减少一个或保持不变，也就是该随机过程的一步转移只能发生在相邻状态之间，或者说，用“生”表示车辆增加一个，“灭”表示车辆减少一个。

假设某时刻系统中已经有n辆车，此时，当有一个批量为k的车辆到来后，系统中的车辆立即增加到n+k个，而事故处每次只能通行一辆车。

该系统在一定条件下是存在平稳分布的，即系统处于各个状态的概率均存在.如果我们根据以前的方法，依据平衡状态下流入流出量相等的原则列出等式，然后根据概率归一化条件求出概率分布，最后根据定义求L等参数会异常复杂。因此，下面我们使用了较为简单的方法求解。

由上面过程我们可以得出交通事故所影响的路段车辆排队长度：

L=L0+L2-L1

四、结束语

本文通过对问题的分析，合理地将问题进行模块化处理，使问题明朗化，并在一定程度上将其进行了简化。所建立的模型不仅适用于本事故，对于一般的城市道路事故也可使用，以便来解决实际问题，更好的舒缓交通，方便大家的通行。

参考文献：

[1]肖华勇.数学建模竞赛优秀论文精选与点评[M].陕西：西安工业大学出版社，2011.

[2]姜启源，金星俊.数学模型[M].北京：高等教育出版社，2011.

[3]曾勇，丽华，建峰.排队现象的建模、解析与模拟[M].陕西：西安电子科技大学出版社，2011.

[4]郭耀煌，钟小鹏.动态车辆路径问题排队模型分析[J].管理科学学报，2006（01）.