高中生数学学习策略的常模及其水平等级标准研究——以天津市为例

李 健，孙 玥，王光明



高中生数学学习策略的常模及其水平等级标准研究——以天津市为例

李 健1，孙 玥2，王光明3

（1．天津师范大学教育科学学院，天津 300387；2．天津港保税区空港学校，天津 300308；3．天津师范大学教师教育学院，天津 300387）

以“高中生数学学习策略调查问卷”为调查工具，采用分层抽样法，对天津市1 124名高中生进行问卷调查．根据问卷调查所得数据，利用原始分数正态化法与公式“”，建立天津市高中生数学学习策略及其子维度策略常模，再结合原则确定对应常模的水平等级标准．应用常模对125名学生组成的群体进行案例分析，除精细加工策略、组织策略、心境管理策略得分明显低于天津市中下水平均值，其余维度得分均处于天津市中等水平附近，并针对各维度提出建议．针对研究结果讨论发现，常模的区域性与时效性特点是影响常模应用的重要因素．

数学学习策略；常模；评价标准；量表；高中

数学是主要研究空间形式和数量关系的科学，其研究内容具有高度的抽象性与逻辑性，常被学生看作“最难学习的科目”[1]．高中数学知识较多、较难，造成许多学生的数学学习效率低下，需要良好的数学学习策略作为高效数学学习的保障[2]．在2016年全国数学教育学术年会上，曹一鸣团队对“中小学数学学业成就测评、影响因素及教学改进”专题进行了深入报告，并指出：数学学习策略与数学学业成绩密切相关．大量研究表明，数学学习策略与数学学业成绩联系紧密，且呈显著正相关关系[3~5]．研究团队的前期成果同样表明：数学学习策略是数学学习效率的影响因素之一[2，6]．由此可见，为减轻高中生过重的学习负担，提高学生数学学业成绩及学习效率，进行数学学习策略研究十分必要．

随着（数学）学习策略相关研究的积累，国内外也编制了许多有影响力的（数学）学习策略测评工具，例如：“学习策略问卷—高中版（LASSI-HS）”（Claire E. Weinstein, David R. Palmer，1990）[7]，“学习动机与策略问卷（MSLQ）”（Pintrich, Paul R. A，1991）[8]，“初中生数学学习策略量表”（莫秀锋，2002）[9]以及“小学生数学学习策略量表”（刘电芝，2003）[10]，但由于调查内容、对象等方面的差异，上述测评工具都不适合对中国高中生直接使用．研究团队基于已有研究成果，对现有问卷题目进行整理与修改，编制了“高中生数学学习策略调查问卷”（王光明，2015）[11]，该问卷内容覆盖全面，且更加针对中国高中生数学学习策略的测量．目前为止，也有一些研究对高中生的数学学习策略进行了测量[12~13]，但都由于缺乏可靠的评价标准，使其研究结果欠缺说服力．在此背景下，对高中生数学学习策略的常模研究便亟待解决．

为提升量表的应用价值，以“高中生数学学习策略调查问卷”为测评工具，拟解决如下问题：（1）确立天津市高中生数学学习策略及其3个主维度常模；（2）根据常模构建对应的水平等级标准；（3）应用所建常模及水平等级标准进行案例分析．

1 测评工具与研究方法

1.1 测评工具

测评工具“高中生数学学习策略调查问卷”属于Likert五点量表，共包含51道题目，由3个主维度（11个子维度）：数学认知策略（复述策略、精细加工策略、组织策略、反馈策略）、数学元认知策略（计划策略、监控策略、反思与调节策略）、数学资源管理策略（时间管理策略、环境管理策略、心境管理策略、外界求助策略），以及测谎题构成，题号具体分布见表1．所有题目选项依次为：A非常符合、B符合、C不确定、D不符合、E非常不符合．问卷整体内部信度为0.96，内容效度为0.91，各结构效度指标也符合标准，可作为测量高中生数学学习策略的有效工具．

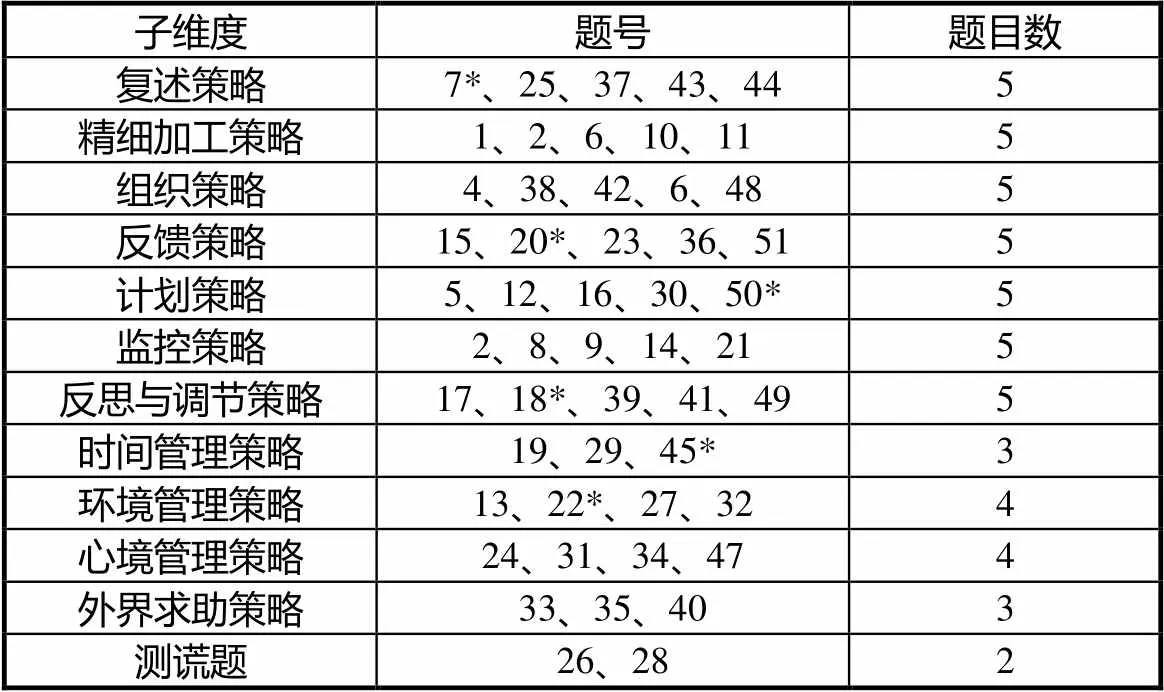
表1 问卷子维度题号分布情况

注：带“*”题目为反向赋分题

1.2 样本选取

样本选取时考虑如下两点：第一，问卷中部分题目涉及高中数学知识，高一学生未必学习过相关内容，高三学生又面临高考，无充裕时间参与测试；第二，个体身心发展规律表明，学生的数学学科能力在高二年级前后将初步定型，其智力水平与逻辑思维基本趋于稳定，个性心理特征更加明显[14]．鉴于以上原因，最终选取天津市高二年级学生作为研究对象，并采用分层抽样法取样．所有样本来自于天津市12个区县的22所高中，共1 124名高二年级学生（数据收集时间：2016.06.01—2016.06.25）．回收问卷1 124份，经过目测剔除答案呈规律性、同一性的问卷41份，再通过可信度检验（测谎题）剔除回答差异性过大的问卷57份，获得有效问卷1 026份，问卷有效率为91.3%，样本分布如表2所示．

表2 样本分布情况

1.3 数据录入与处理

录入数据时，正向赋分题依选项A、B、C、D、E分别赋值5、4、3、2、1分，反向赋分题分别赋值1、2、3、4、5分，分值越小，表明对应的数学学习策略水平越低，反之数学学习策略水平越高．问卷中26题与28题为测谎题（26与8题对应，28与50题对应），若某问卷中26与8题的作答不一致，或对28与50题的作答不一致，该问卷视为无效问卷．

录入数据后，采用SPSS18.0进行数据处理，得到天津市高中生数学学习策略及各子策略的总体特征，再依照“原始分数正态化”处理法将原始分数转化为标准分数，并借助公式“=50+10”进行转换，确立分数常模，最后依据原则确立数学学习策略及各子策略的水平等级标准．

2 研究过程与结果

2.1 研究过程

2.1.1 数学学习策略常模及其水平等级标准的确立

首先，通过计算1 026名被试学生的百分等级，确定原始分数与百分等级间的对应关系，再利用正态分布表，借助已知百分等级反查其对应的标准分数值．为避免分数值出现负数或过小所带来的不利影响，利用公式=50+10对分数进行线性变换．最终获得天津市高中生数学学习策略水平常模（表略）．

由于高中生数学学习策略受数学认知策略、数学元认知策略、数学资源管理策略3个主维度的影响，为更具针对性地分析与诊断数学学习策略，下文将分别确立3个主维度的常模及其水平等级标准．

表3 天津市高中生数学学习策略水平等级标准

2.1.2 数学认知策略常模及其水平等级标准

先从问卷中挑选出数学认知策略维度下的20道题目（见表4），再依据天津市高中生数学学习策略常模的构建方法，建立天津市高中生数学认知策略常模（表略）．

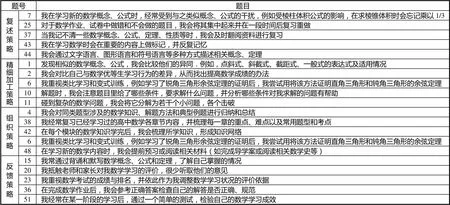
表4 数学认知策略题目

参照数学学习策略水平等级的划分方法，对数学认知策略进行类似划分（见表5），再分别计算不同水平等级内高中生在其4个子维度（复述策略、精细加工策略、组织策略、反馈策略）上的平均得分，可得到天津市高中生数学认知策略四因子分数柱状图（图1）．在图1的基础上，结合数学学习策略子维度的操作概念界定[11]，对于不同水平等级数学认知策略的天津市高中生，大致特点是：优秀等级学生能有效地加工与整理信息，可对信息分门别类地进行系统性储存；中上等级学生能较好地完成信息加工与整理，可对部分信息进行储存；中等水平学生能基本完成信息的加工与整理，信息储存能力一般；中下等级学生对信息的加工与整理存在较大偏差；差等级学生基本无法对信息进行有效地加工与整理．

表5 天津市高中生数学认知策略水平等级标准

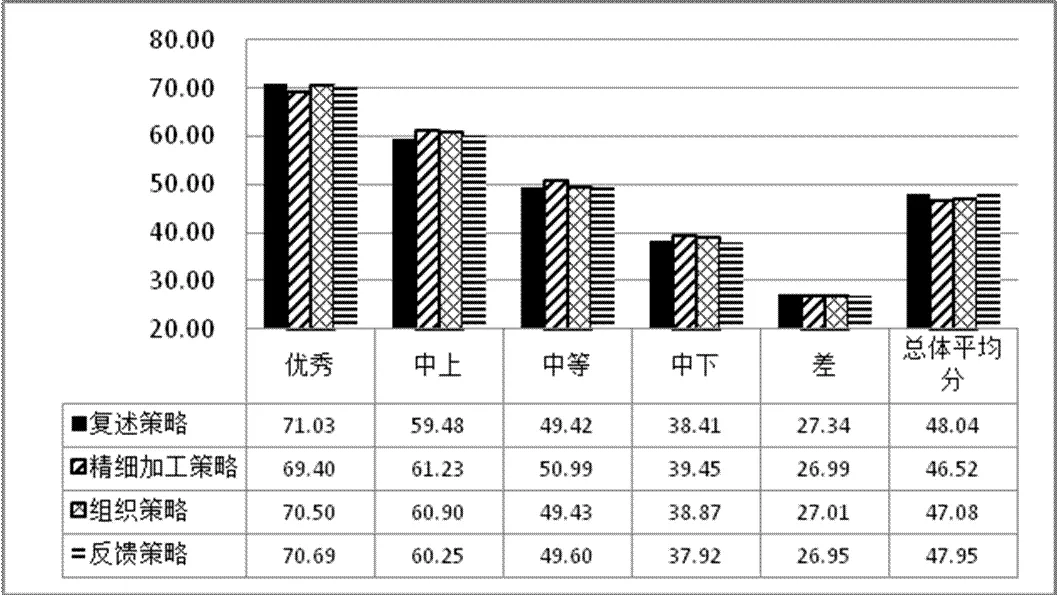
图1 天津市高中生数学认知策略四因子T分数柱状图

2.1.3 数学元认知策略常模及其水平等级标准

先从问卷中挑选出数学元认知策略维度下的15道题目（见表6），再依据高中生数学学习策略水平常模的构建方法，建立天津市高中生数学元认知策略常模（表略）．

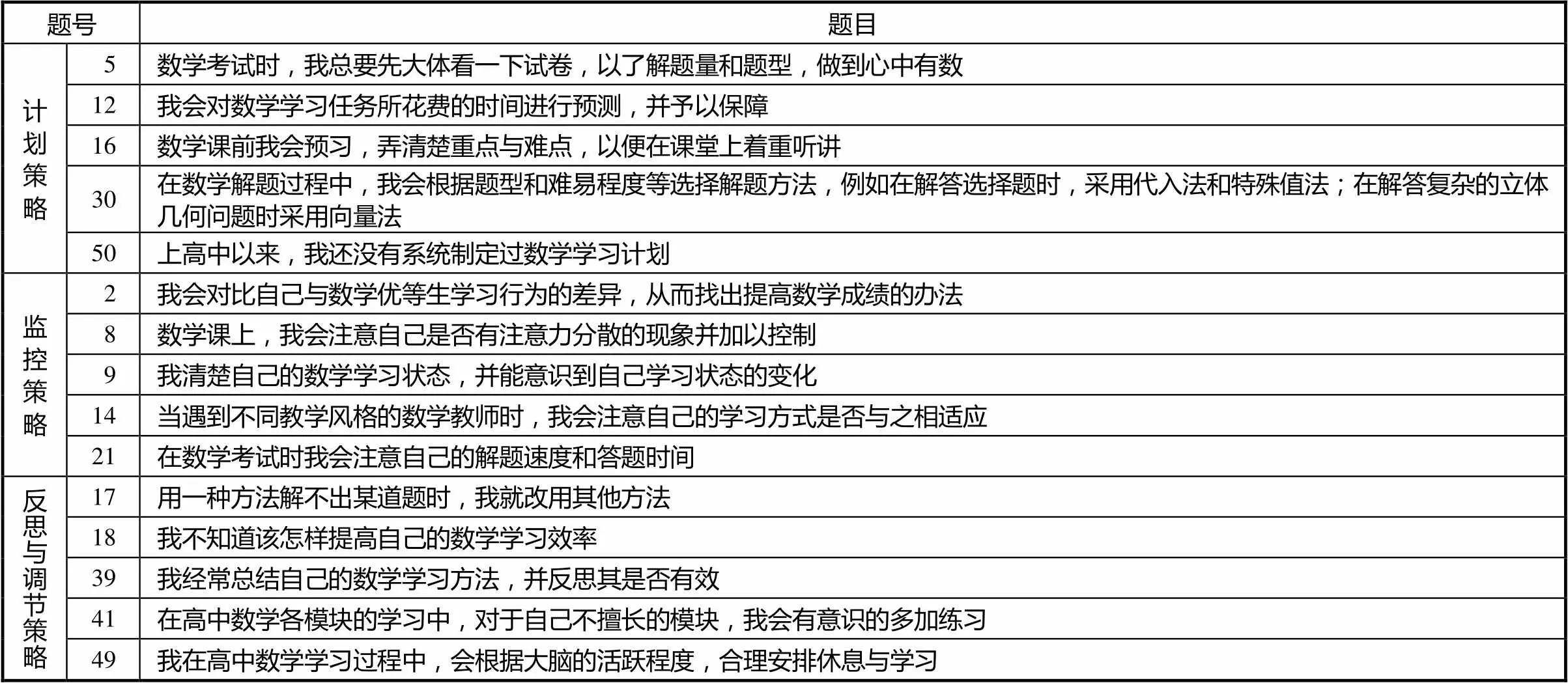
表6 数学元认知策略维度

参照数学学习策略水平等级的划分方法，对数学元认知策略进行类似划分（见表7），再分别计算不同水平等级内高中生在其4个子维度（计划策略、监控策略、反思与调节策略）上的平均得分，可得到天津市高中生数学元认知策略三因子分数柱状图（图2）．在图2的基础上，结合数学学习策略子维度的操作概念界定，对于不同水平等级数学元认知策略的天津市高中生，大致特点是：优秀等级学生能对自我认知过程进行积极自觉地监控和调节；中上等级学生具有较好地安排与调节学习过程的能力；中等水平学生基本能完成自我监控与调节；中下等级学生能了解自我认知过程，具有监控和调节的意识，但完成性较差；差等级学生基本不能了解与控制自我认知过程．

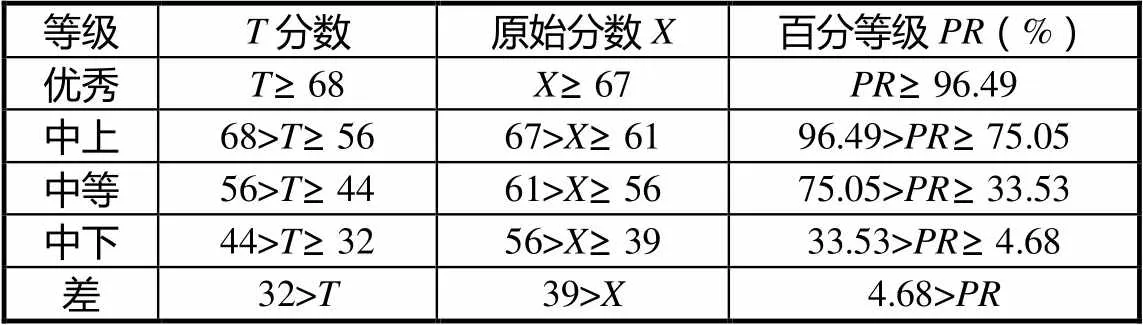
表7 天津市高中生数学元认知策略水平等级标准

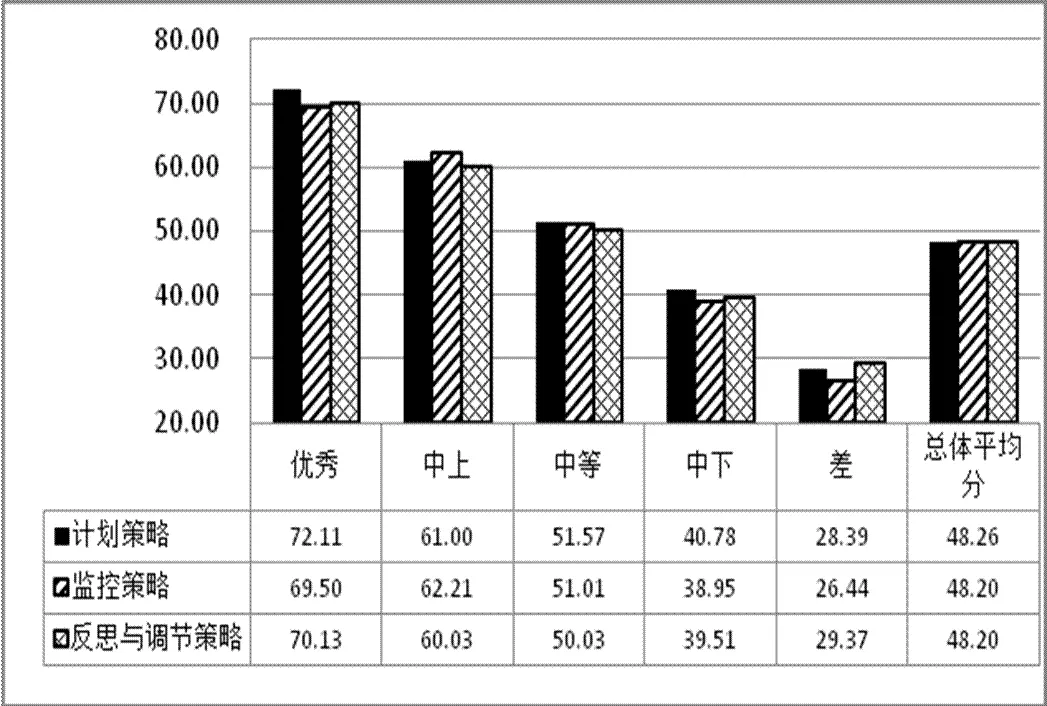
图2 数学元认知策略三因子T分数柱状图

2.1.4 数学资源管理策略常模及其水平等级标准

先从问卷中挑选出数学资源管理策略维度下的14道题目（见表8），再依据数学学习策略水平常模的构建方法，建立天津市高中生数学资源管理策略常模（表略）．

参照数学学习策略水平等级的划分方法，对数学资源管理策略进行类似划分（见表9），再分别计算不同水平等级内高中生在其4个子维度（时间管理策略、环境管理策略、心境管理策略、外界求助策略）上的平均得分，可得到天津市高中生数学资源管理策略四因子分数柱状图（图3）．在图3的基础上，结合数学学习策略子维度的操作概念界定，对于不同水平等级数学资源管理策略的天津市高中生，大致特点是：优秀等级学生能合理安排时间，适应环境及调节心境，并善于利用外界资源辅助数学学习；中上等级学生能较好地适应环境，并利用资源改善学习；中等水平学生能对所处环境加以调节并适当利用学习工具；中下等级学生的不能较好地适应环境，对资源的利用能力也有所欠缺；而差等级学生基本无法适应所处环境，不能合理利用学习资源．

表8 数学资源管理题目

表9 天津市高中生数学资源管理策略水平等级标准

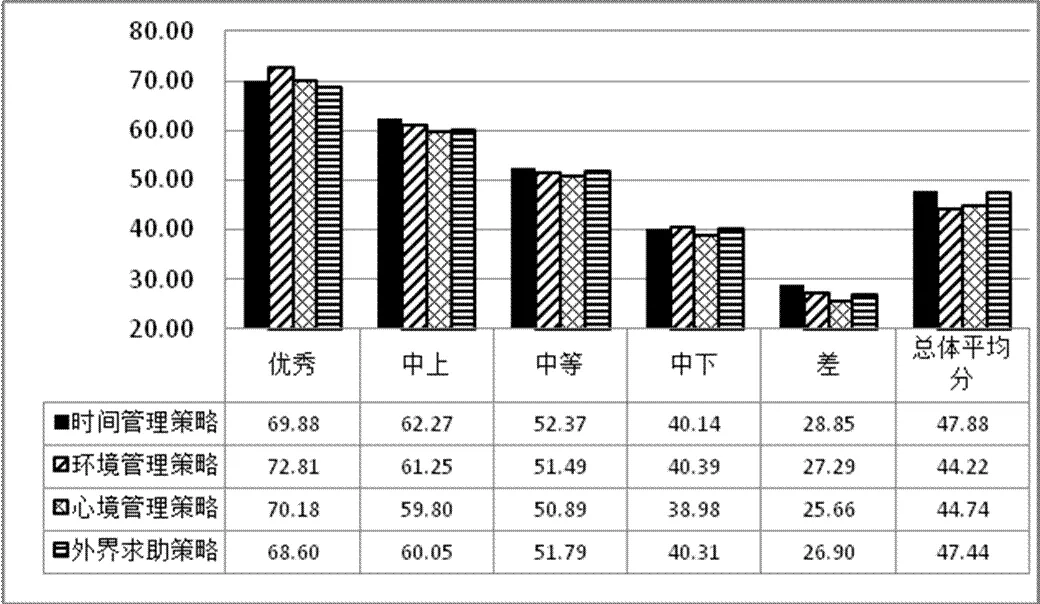
图3 天津市高中生数学资源管理策略四因子T分数柱状图

2.2 常模及水平等级标准的应用案例

天津市高中生数学学习策略常模及其水平等级标准的确立，为天津市高中生的数学学习策略水平的评价提供了标尺．以下将应用该研究成果，对天津市某中学的高中生群体进行诊断分析．

2.2.1 总体情况

被试学生选自天津市某重点中学高二年级的3个普通班（共计125人），其数学学习策略水平情况见表10，在不同子策略上的平均分见表11．现将此125名学生视为一个整体，与全市学生进行比较分析，用以了解该群体的数学学习策略大致水平．被试群体的数学学习策略原始平均分为161.67，将其与表3对照，可知被试群体的数学学习策略处于天津市中等水平．以下将分别从3个主维度入手，对被试群体作进一步地诊断分析．

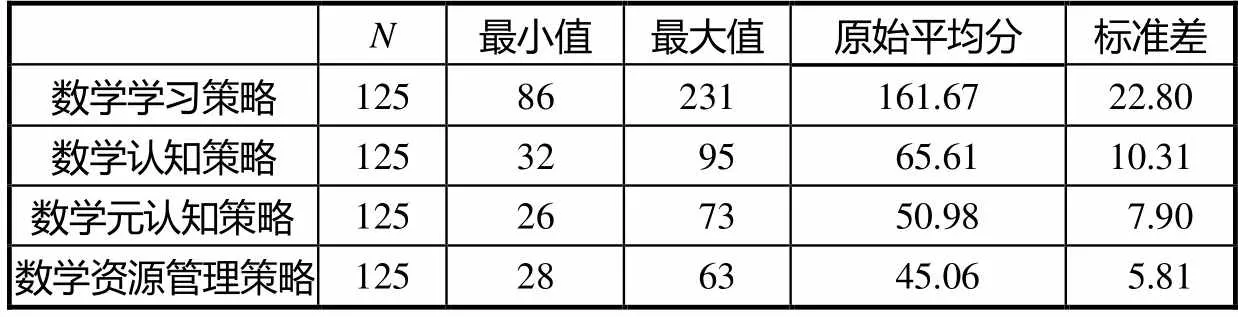
表10 被试学生数学学习策略水平情况

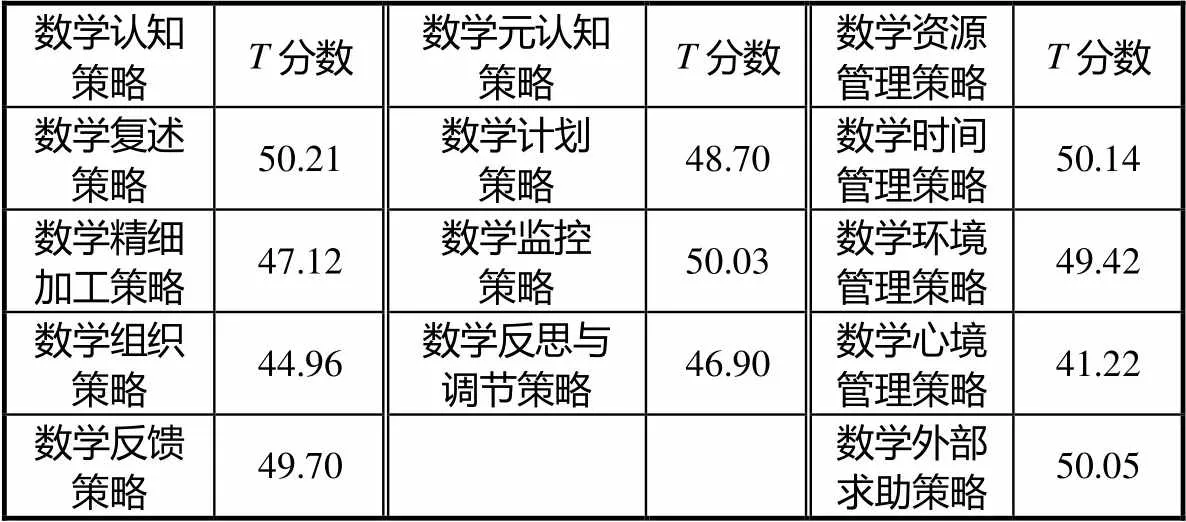
表11 被试学生在各数学学习子策略上的T分数平均分

2.2.2 数学认知策略的诊断与建议

结合表11与图1中的数据分析可知：在复述策略、反馈策略上，被试群体与天津市高中生中等水平基本相当，但在精细加工策略、组织策略上低于天津市高中生中等水平（见图4）．

数学认知策略的改进建议：在培养学生的数学认知策略时，应着重提升其精细加工策略、组织策略．具体到该群体中学习策略中等及其以下水平的学生：对于中等水平学生，教师应注重各章节内容间的过渡，帮助学生形成清晰的知识网络结构．对于中下等水平学生，教师应注重其对基本概念的理解，帮助学生理解问题的本质，采取恰当的表征方式，辅助学生构建有意义的学习．对于差等级学生，教师首先应帮助其理解并记忆相关数学概念及基本解题方法，让学生明确使用哪些基本策略可解决哪类问题，再通过变式练习、多元表征等方法促进学生对知识点的理解．

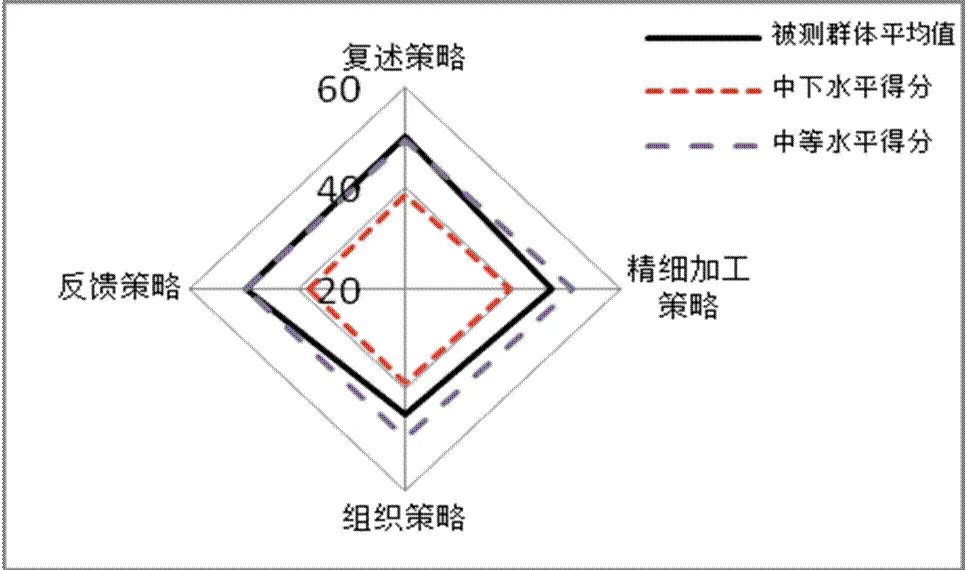
图4 被试群体的数学认知策略四子维度T分数图

2.2.3 数学元认知策略的诊断与建议

结合表11与图2中的数据分析可知：在认知策略、监控策略、反思与调节策略上，被试群体都略微低于天津市高中生中等水平，但差距并不明显（见图5）．

数学元认知策略的改进建议：对于高中生计划策略的提高，可以有如下具体措施，例如让学生注意预估做题耗时，对做题时间的快慢保持敏感；注意培养学生良好的课前预习习惯，课前明确教学的重、难点，提高听课质量；要求学生制定单元和学期的学习计划，有条理、有节奏地学习数学．对于高中生监控策略、反思与调节策略的提升，教师应提供给学生一些具体有效的方法，帮助学生进行自我监督和调控，例如让学生对比自己与数学优等生学习行为的差异，从而找出提高数学成绩的办法；让其了解自身数学学习状态，并能意识到自己学习状态变化等．

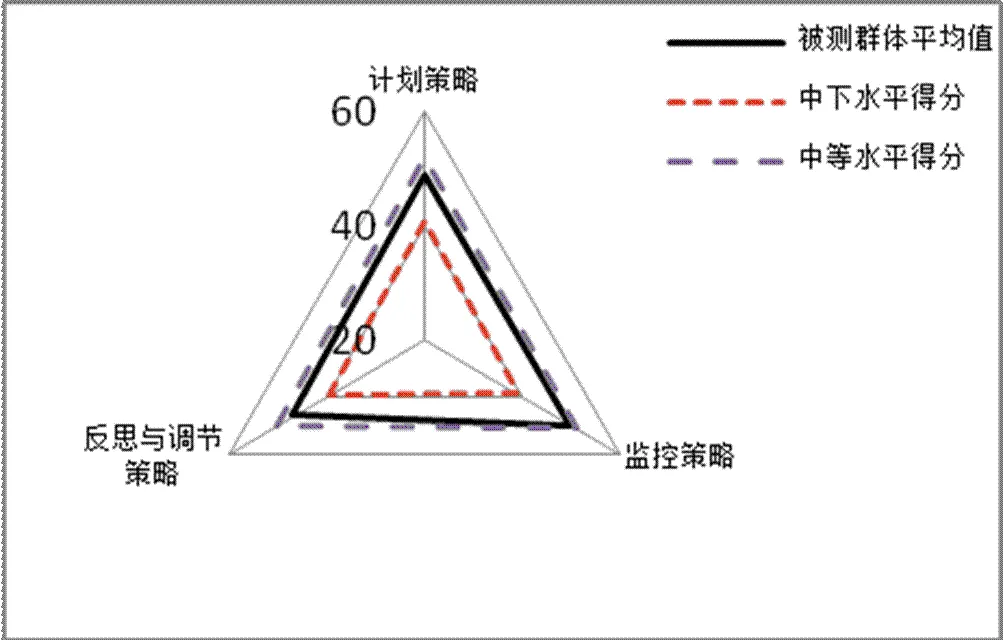
图5 被试群体的数学元认知策略三子维度T分数图

2.2.4 数学资源管理策略的诊断与建议

结合表11与图3中的数据分析可知：在时间管理策略、环境管理策略、外界求助策略上，被试群体略低于天津市高中生中等水平，但相差并不明显；而在心境管理策略上，被试群体仅略高于天津市高中生中下水平（见图6），较为不足．

数学资源管理策略维度改进建议：根据被试学生的分值，可重点关注其心境管理策略，关注学生的心理波动，帮助学生调节情绪，并组织学生开展适当的自我性格及能力的认知活动．具体而言，教师应有意避免学优生过渡追求完美、不允许失败等心理的产生，否则会滋生该类学生的焦虑情绪；对于学困生，教师应时常注意其心理压力的疏导，使其积极地面对目前的学习状态，避免学生因以往成绩不佳而产生惧怕考试、厌恶数学学习．

图6 被试群体的数学资源管理策略四子维度T分数图

应用数学学习策略常模对天津市某校做数学学习策略诊断，并给出建议，受到了基础教育应用校的高度欢迎，说明“天津市高中生数学学习策略水平的常模表”具有较好的应用性和可推广性．

2.3 研究结果

通过研究得到了天津市高中生数学学习策略常模与水平等级标准．当某学生（或群体）原始分数高于213分时，表明其处于“优秀”等级，意味着该生（或群体）的数学学习策略水平超过天津市地区约96.49%的学生；当原始分数介于176~213之间时，表明该生（或群体）的数学学习策略水平处于“中上”水平，有接近73.78%~96.49%学生的数学学习策略低于该生（或群体）．同理可分析得出“中等”、“中下”及“差”等级学生的数学学习策略水平情况．

对于数学学习策略各主维度的常模与水平等级标准，也有相应研究结果．例如：若某学生（或群体）在数学认知策略维度上的测试成绩为61分，则表明该生（或群体）处于全市“中等”等级，其数学认知策略水平高于全市29.43%的学生，能基本完成信息的加工与整理，信息储存能力一般．若某学生（或群体）在数学元认知策略维度上测试成绩为61分，则表明该生（或群体）的数学元认知策略处于全市“中上”等级，高于全市75.05%的学生，具有能较好地安排与调节学习过程的能力．若某学生（或群体）在数学资源管理策略维度上的测试成绩为59分，则表明该生（或群体）处于全市“优秀”等级，高于全市96.59%的学生水平，能有效管理时间、环境、心境，并善于利用外界资源辅助数学学习．

3 讨 论

研究结果还展现出一个特别现象，即被测学校学生的历年高考成绩位于全市前列，但调查结果表明被试学生的数学学习策略水平并不十分理想，数学学习策略与其数学成绩之间的相关性并不明显，这与凡森泉[12]、张爽[15]等人的研究并不一致．对于这一问题，除了应考虑到这一研究成果仅能代表天津市的当前高中生数学学习策略现状，与以往研究存在地域差异、时间差异，还应注意到至少以下两点：第一，不能仅以历年该校学生位于全市前列的高考成绩，推测出被试学生的数学学习成绩也高于同期天津市高中生，两者间并无直接关联．第二，数学学习策略的高低并不能完全决定学生数学学习成绩的好坏，它仅是影响数学学习成绩心理结构的因素之一．这也侧面印证了数学学习的心理结构模型包含诸多因素的结论[5，16~22]．所以，被试学生数学学习成绩优异而数学学习策略并没有显现出等同的高水平，可能与其它数学学习心理结构要素有关[23~59]．

目前为止，针对中国高中生的数学学习策略常模研究并不多见，这一研究不仅完成了高中生数学学习策略常模的研制，还划分了相应的水平等级标准，丰富了数学学习策略领域的研究成果，为后继研究提供了定量化比较的标准．研究成果可用于天津或相近教育水平地区高中生的数学学习策略诊断，明确学生或群体的数学学习策略（及各维度）水平，为其数学学习策略的培养与提升提出合理建议．但作为常模研究，也应注意到该研究成果的区域性与时效性特点．区域性特点，是指研究所确立的常模与水平等级标准是以天津市高中生为调研对象，研究成果仅供天津市及相近教育水平地区参考使用．时效性特点，是指随着社会、科技、经济的快速发展，对于当前教育教学的影响颇大，间接地影响着不同时期高中生的数学学习策略，研究所确立的常模与水平等级标准仅能反映近段时期内天津市高中生的数学学习策略水平．

4 结 论

研究所构建的天津市高中生数学学习策略常模及其水平等级标准，进一步拓展了高中生数学学习策略的实践研究，为指定区域高中生的数学学习策略评价提供了标尺．在总体常模及水平等级标准的基础上，分别建立了3个一级维度的常模与水平等级标准，为教师更为细致地诊断高中生的数学学习策略水平提供了帮助．运用研究所得水平等级标准，对125名高中生构成的群体进行了诊断分析，除了心境管理策略略高于天津市中下水平，精细加工策略与组织策略低于天津市中等水平，其余子策略均处于天津市中等水平附近，并提出相应提升建议．

在具体应用研究所得常模与水平等级标准时，调查对象应来自天津市或相近教育水平地区，并注意该常模具有时效性特点．在未来研究中，希冀在全国范围内选取代表性样本，确立中国高中生数学学习策略水平常模；并应关注常模使用的时效，根据地区的教育状况和学生发展变化，定期适时修改常模，以及建立对应的水平等级标准．

[1] 华志远．辩证认识数学抽象探求有效教学策略[J]．数学通报，2004，（11）：12-14．

[2] 廖晶，王光明，黄倩，等．高中生高效率数学学习策略特征及对数学学业水平的影响路径[J]．数学教育学报，2016，25（5）：61-66．

[3] 莫秀峰，刘电芝．初中生数学学习策略的个体差异研究[J]．数学教育学报，2007，16（4）：56-58．

[4] 王桂云，沈自飞．关于高职生数学学习策略的研究与思考[J]．数学教育学报，2005，14（2）：101-103．

[5] 王光明，李健，康玥媛．小学数学教材中分数意义的呈现：历史顺序与“超回归”倒序的统一[J]．课程·教材·教法，2017，（5）：34-39．

[6] 王光明，佘文娟，宋金锦．基于NVivo10质性分析的高效数学学习心理结构模型[J]．心理与行为研究，2014，（1）：74-79．

[7] Weinstein C E, Palmer D R.[M]. Clearwater, FL: H & H Publishing, 1990.

[8] Pintrich P R. A Manual for the Use of the Motivated Strategies for Learning Questionnaire (MSLQ) [EB/OL]. http://files.eric.ed.gov/fulltext/ED338122.pdf. The Regents of the University of Michigan,1991.

[9] 莫秀峰．初中生数学学习策略的发展特点及可控心理影响因素研究[D]．西南师范大学，2002．

[10] 刘电芝．小学儿童数学学习策略的发展与加工机制研究[D]．西南师范大学，2003．

[11] 王光明，廖晶，黄倩，等．高中生数学学习策略调查问卷的编制[J]．数学教育学报，2015，24（5）：25-35．

[12] 凡森泉．高中不同数学学习成绩学生的学习策略调查研究[D]．南京师范大学，2015．

[13] 刘兴宇．高中学生数学学习策略研究[D]．西北师范大学，2003．

[14] 林崇德．论学科能力的建构[J]．北京师范大学学报（社会科学版），1997，（1）：5-12．

[15] 张爽．高一学生数学学习兴趣、成就目标定向、学习策略与学业成绩的关系研究[D]．东北师范大学，2006．

[16] 康玥媛，张楠，王光明，等．高效率数学学习高中生数学成绩的影响路径[J]．心理与行为研究，2016，（3）：352-359．

[17] 王光明，佘文娟，廖晶，等．高效率数学学习高中生的元认知特征及其教学意义[J]．教育科学研究，2017，（4）：46-53．

[18] 王光明，张晓敏，王兆云．高中生高效率数学学习的智力特征研究[J]．教育科学研究，2016，（3）：48-55．

[19] 王光明，张楠，周九诗．高中生数学素养的操作定义[J]．课程·教材·教法，2016，（7）：50-55．

[20] 郭衎，曹一鸣，王立东．教师信息技术使用对学生数学学业成绩的影响——基于三个学区初中教师的跟踪研究[J]．教育研究，2015，（1）：128-135．

[21] 王光明，张楠，康玥媛．数学教师培训视域下的教育软件培训内容研究[J]．教育理论与实践，2015，（35）：35-37．

[22] 曹一鸣，郭衎．中美教师数学教学知识比较研究[J]．比较教育研究，2015，（2）：108-112．

[23] 吴骏．基于HPM教学的学生认知发展个案研究[J]．数学教育学报，2017，26（2）：46-49．

[24] 徐文彬，彭亮．中国数学教育哲学研究的回顾与反思（2000—2015）——兼论数学文化的教育哲学探索[J]．数学教育学报，2017，26（2）：60-65．

[25] 曾峥，杨豫晖，武金艳．数学“四基”的研究现状及展望[J]．数学教育学报，2017，26（2）：66-70．

[26] 聂晓颖，黄秦安．论数学课堂文化的内涵与模式及对培养数学核心素养的价值[J]．数学教育学报，2017，26（2）：71-74．

[27] 杜宵丰，刘坚．八年级学生“数学兴趣”“数学自我效能感”“学习坚持性”与“数学成就”的关系研究[J]．数学教育学报，2017，26（2）：29-34．

[28] 常磊，鲍建生．情境视角下的数学核心素养[J]．数学教育学报，2017，26（2）：24-28．

[29] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19-23．

[30] 刘荣玄，朱少平．概念图引导型构图题的研究与实践[J]．数学教育学报，2017，26（2）：86-91．

[31] 曹一鸣，于国文．中学数学课堂教学行为关键性层级研究[J]．数学教育学报，2017，26（1）：1-6．

[32] 何小亚．高中概率模型学与教中的问题和对策[J]．数学教育学报，2017，26（1）：37-40．

[33] 刘咏梅，吴立宝．信息技术对促进数学基本思想教育的价值分析[J]．数学教育学报，2017，26（1）：41-46．

[34] 伍春兰．基于学生思维培养的数学定理教学的调查与分析——以“圆周角定理”教学设计为例[J]．数学教育学报，2017，26（1）：55-58．

[35] 高欢，陈克胜．数学自我效能感的研究现状与展望[J]．数学教育学报，2017，26（1）：76-81．

[36] 张玉峰，智红燕，付夕联．数学直觉的作用[J]．数学教育学报，2017，26（1）：82-87．

[37] 顾继玲．聚焦“基本数学活动经验”[J]．数学教育学报，2016，25（1）：34-37．

[38] 方均斌，梁凯，朱玲．数学问题教学的五个探索点[J]．数学教育学报，2016，25（1）：47-50．

[39] 朱哲民，贾冰．数学探究教学SIRA评价标准建立的尝试[J]．数学教育学报，2016，25（1）：57-60．

[40] 朱立明，马云鹏．学生数学符号意识PORE评价框架的构建[J]．数学教育学报，2016，25（1）：84-88．

[41] 李兴贵，王新民．数学归纳推理的基本内涵及认知过程分析[J]．数学教育学报，2016，25（1）：89-91．

[42] 史宁中．试论数学推理过程的逻辑性——兼论什么是有逻辑的推理[J]．数学教育学报，2016，25（4）：1-16．

[43] 孙旭花．中国数学教育优势：隐性的代数教学设计模型[J]．数学教育学报，2016，25（5）：5-8．

[44] 徐章韬，汪晓勤．HPM教育价值剖析及应用取向的深度挖掘[J]．数学教育学报，2016，25（6）：10-14．

[45] 王立东，郭衎，孟梦．认知诊断理论在数学教育评价中的应用[J]．数学教育学报，2016，25（6）：15-18．

[46] 董连春，曹一鸣．攀登数学教育研究高峰——第39届国际数学教育心理学大会综述[J]．数学教育学报，2016，25（2）：1-2．

[47] 郑毓信．数学教育视角下的“核心素养”[J]．数学教育学报，2016，25（3）：1-5．

[48] 喻平．数学学科核心素养要素析取的实证研究[J]．数学教育学报，2016，25（6）：1-5．

[49] 刘祖希．访曹一鸣教授：谈青年数学教育工作者培养等问题[J]．数学教育学报，2016，25（3）：44-47．

[50] 曹广福，张蜀青．论数学课堂教学与评价的核心要素——以高中导数概念课为例[J]．数学教育学报，2016，25（4）：17-20．

[51] 范良火，熊斌，李秋节．现代数学教育中的教材研究：“概念”“问题”和“方法”[J]．数学教育学报，2016，25（5）：1-5．

[52] 何光峰，李美娟．TIMSS数学录像课研究及其借鉴意义[J]．数学教育学报，2016，25（5）：88-90．

[53] 韩仁生，王毓珣．中学生数学学习成就归因的性别差异比较研究[J]．数学教育学报，2016，25（4）：21-24．

[54] 李娜，莫雅慈，吴立宝．初中数学课堂中教师对学生错误反馈的类型研究——基于24节录像课的分析[J]．数学教育学报，2016，25（5）：55-57．

[55] 郑毓信．“数学与思维”之深思[J]．数学教育学报，2015，24（1）：1-5．

[56] 谢明初．数学教育的人文追求[J]．数学教育学报，2015，24（1）：6-8．

[57] 何小亚．学生“数学素养”指标的理论分析[J]．数学教育学报，2015，24（1）：13-16．

[58] 刘琳娜．把握数学学科本质 实现高效课堂教学[J]．数学教育学报，2015，24（5）：71-73．

[59] 韩云桥．论数学学习的经验性思维[J]．数学教育学报，2015，24（5）：51-54．

Norm and Level Standard Research of High School Students’ Mathematics Learning Strategies——A Case Study of Tianjin

LI Jian1, SUN Yue2, WANG Guang-ming3

(1. College of Educational Science, Tianjin Normal University, Tianjin 300387, China;2. Airport School of Tianjin Bonded Area, Tianjin 300308, China;3. Teacher Education College, Tianjin Normal University, Tianjin 300387, China)

By theand stratified sampling method, a questionnaire survey was conducted among 1 124 high school students in Tianjin. Based on the data, we construct a norm of high school students’ mathematics learning strategies in Tianjin and three sub-dimensional norms, which were used by raw score normalization method and formula “=50+10*”. And then, we got a Level Standard by utilizing 6principle. A case analysis was conducted among 125 students, and the results showed that besides elaborate processing strategy, organizational strategy and mood management strategy were below the average of Tianjin, other dimensions were around the average of Tianjin, and some corresponding suggestions were proposed. On the results, we found the regionalism and timeliness of norm were significant influence factors when we used norm.

mathematics learning strategy; norm; the criterions of evaluation; scale; high school

[责任编校：周学智]

G449

A

1004–9894（2017）04–0008–07

2017–06–16

天津市哲学社会科学规划重点项目——立德树人背景下中学生学科核心素养测评——以语数外为例（TJJX16-007）

李健（1988—），男，重庆人，博士生，主要从事数学课程与教学论研究．王光明为本文通讯作者．