中学数学教研员的“专业知识”“能力”及其“发展”

章建跃，黄荣金，赵文君，莫雅慈，吴增生，周远方



中学数学教研员的“专业知识”“能力”及其“发展”

章建跃1，黄荣金2，赵文君3，莫雅慈3，吴增生4，周远方5

（1．人民教育出版社，北京 100081；2．美国中田纳西州立大学数学系，美国；3．香港大学教育学院，香港；4．浙江省仙居县教研室，浙江台州 317300；5．湖北省教育科学研究院，湖北武汉 4300715）

先让中学数学教研员对PKC发展现状进行自评，并对PKC的期望及其发展途径作出评价；然后通过开放性问题收集了教研员对PKC维度和PKC发展途径的补充意见；再通过多种量化分析方法，探索了教研员PKC的特征、教研员对PKC的期望、教研员的基本信息、教研员的PKC发展自评等之间的关系．结果表明，被试认同研究提出的PKC六维模型．虽然在不同维度的发展上存在差异，但总体而言，教研员对自己PKC的发展很有自信．因素分析显示，模型的6个维度可以进一步归纳为两个部分：（1）关于教与学的知识以及在指导和领导方面的能力；（2）关于学习内容、学生评价和信息技术运用方面的知识．被试认为，他们的专业发展途径包括：通过阅读、参加培训活动、参与和指导学校和跨地区的教研活动、观察和讨论课堂以及通过网络学习共同体进行经验分享，中学数学教研员专业水平的提升是这些途径共同作用的结果．

中国课例研究；教研活动；中学数学教研员；专业知识和能力；专业发展

1 研究缘起

近年来，中国学生在各种国际数学水平测试、数学竞赛中屡创佳绩，引发了学者们对中国中小学数学教学的研究热，课例研究（lesson study）是被关注的焦点之一．“课例研究”概念由日本首先提出，随后以不同形式在世界各地逐步传播[1]，它在促进学生学习和教师成长方面的作用已被广泛证实[2]．研究表明，课例研究取得成功的一个重要原因是专家学者（knowledgeable others）的深度参与[3~7]．一般而言，课例研究包括研究教学材料和制定目标、设计研究课、执行和观察研究课、反思和修改研究课等环节[8]．由于在实施过程中有不同的目标和关注点，课例研究也各有不同．例如，有研究认为[9]，中国的课例研究注重“同课异构”，并且专家的参与是必不可少的[10]．

中国有专门的包含省、地（市）、县（区）等各级教研室的教研工作管理系统，这个系统中的教研员通过有计划的、形式多样的教研活动，组织不同层级的课例研究，从而为中国教师专业发展提供有效支持[11~12]（需要说明一点：“教研员”是中国特有的名称，所以在文献中用“教师教育工作者”（teacher-educator)，其他处用“教研员”）．在中国，教研员是一个特殊的岗位．1957年，教育部颁布的《中学教研组工作条例（草案）》里明确了教研员的任职标准，中国教育学会中学数学教学专业委员会在教研工作指导意见中也明确了教研员应履行的职责和任职条件等，但是关于教研员到底需要具备哪些知识和能力，以及他们如何提升自己的专业水平等，人们知之甚少；教研员在课例研究中的重要性有目共睹，但对于教研员是如何指导研究课的，他们是如何在课例研究中与教师开展合作的等关注不够[13]．为此，研究将以中国中学数学教研员为研究对象，从内部人士的视角观察教研员所应具备的知识、能力以及有效提升专业水平的途径．

2 研究背景和理论基础

2.1 数学教学知识

在过去的20年里，有大量的研究关注教师的数学教学知识[14~16]，其中舒尔曼提出的内容知识（CK）和学科教学知识（PCK）是很多研究的核心理论，其他理论也受到一定的关注．例如，通过完善舒尔曼的模型，波尔（Ball）和他的同事[14]提出数学教学知识，包括一般的内容知识和特殊的内容知识、关于内容和学生的知识以及关于内容和教学的知识．第一个关于数学教学知识的大型研究关注职前教师的内容知识、学科教学知识和一般教学法知识．

马立平认为[17]，中国在职小学教师对数学知识有良好理解，体现在连贯性、整体性和灵活性3个方面．然而，通过对师范专业课程体系的研究，人们发现中国数学教师职前培养工作集中在对数学学科内容知识和逻辑思维的准备上，较少关注一般教学法知识和教学实践．通过对全国中学数学教师资格考试的研究，研究者指出[18]，该测试在学科内容知识和学科教学知识方面有很高的要求．

对数学内容的重视是中国数学教师职前培训的一个传统．研究者指出，数学教学知识可以在教师入职后通过多种途径得到充实，例如入职时建立的师徒制、各种有计划的教研活动以及目前非常普遍的名师工作室机制．在各种教研活动中，课例研究是核心[10]．事实上，课例研究不仅成为教师提高数学教学知识水平的有效方法，而且也是促进教师从新手教师向成熟教师发展的有效途径[11，17]．

2.2 教师教育工作者的知识和能力

虽然教师教育工作者要具备的知识和能力（PKC）的研究还未引起学者的广泛关注，但这是一个正在发展的新兴领域[19]．一些模型尝试着对教师教育工作者的知识进行定义，例如：Jaworski的教学框架[20]包括数学学习环境的3个方面：数学的挑战（the mathematical challenge）、学习的组织（the management of learning）和对学生的敏感度（the sensitivity to students）．在此基础上，Zaslavsky and Leikin[21]提出了教师教育工作者知识，包括为数学教师提供有挑战的内容、组织数学教师学习活动和对数学教师的敏感度．从社会文化的角度，Perks and Prestage[22]定义了教师知识的3个方面：实践智慧（practical wisdom）、专业传统（professional tradition）和学习者知识（learner knowledge），所有这些方面综合起来影响教师对课堂事件的决策．进一步地，教师教育工作者知识的模型包括学习者知识（learner knowledge）、实践智慧（practical wisdom）和专业传统（professional tradition），学习者知识就是前面3个方面的教师知识，实践智慧指从数学教育培训中学到的知识，专业传统指从已有的教师教育课程及数学教学研究中积累的知识．这些模型反映了教师教育工作者知识的复杂性．除此之外，教师教育工作者需要知道如何帮助职前教师高效地进行教学[23]．

进一步的，研究者探索了教师教育工作者需要具备的特殊能力．在众多的要求中，做一个反思的实践者是最基本且最重要的[24~25]．具体而言，教师教育工作者需要能够：（1）发展适应性（develop adaptability）；（2）培养相似和不同的意识（foster awareness to similarities and differences）；（3）处理冲突、困境和问题；（4）从实践中学习；（5）选择、使用适当的工具和资源进行教学；（6）识别和解决学生学习中的困难；（7）分享和表达自己、同事及学生的感受．

然而，大部分关于教师教育工作者PKC的研究关注了大学数学教师是如何培养职前教师的，少量的研究探索了实际从事教师发展工作所需要具备的知识和能力[26~27]．Sutton等[28]提出了一个关于教师教育工作者需要具备的八维的PKC框架：教师学习、教师发展、教师实践、学生学习、评价、交流、关系和领导力．

2.3 中国数学教研员PKC的研究

基于中国官方文件对教研员的要求，黄荣金等[26]指出中国教研员需要在高效教学、教学研究、有效组织学校层面的教学活动并评价教师的教和学生的学等几个方面具有专业性．进一步的，中国教育学会中学数学教学专业委员会[29]特别强调了教研员在发现和培养骨干教师以及给教育行政部门提供政策咨询的角色．一些研究试图定义中国教研员的核心能力．例如，何晓波[30]提出教研员核心能力系统这一概念，包括教师所具有的一般能力，如上课评课、命题评价、协调沟通，语言表达等能力，以及与教研员工作性质相适应的特殊能力，包括教研力、科研力、执行力、管理力和创新力．罗斌[31]从教研员的核心素养角度提出了一个三维基本框架，包括专业精神、专业知识和专业能力．专业精神包括专业意识和专业情怀；专业知识包括学科专业知识、学科教研知识、教师教育知识、课程知识；专业能力包括课程建设与资源开发能力、教学研究与指导改进能力、质量评价与分析反馈能力、教育教学科研能力．综上所述，不同的框架都强调了教研员知识和能力的几个核心要素：学科知识、教研活动指导、进行教育研究和领导力．然而，这些框架都是基于教研员的工作经验提出的，缺乏关于中国数学教研员PKC的实证研究．

2.4 教师教育工作者PKC的发展

很多研究都提出了有效的教师专业发展的途径[32]，但对如何提升作为教师专业发展支持者的教师教育工作者的专业性却很少被提及[25，33]．研究表明，持续地对行动和在行动中进行反思是一个教师教育工作者学习的重要特征．Zaslavsky[25]指出，教师教育工作者通过设计任务和反思教师的工作来学习，在她的模型中，起关键中介作用的是数学任务．进一步的，建立在实践共同体的概念下，Cochran-Smith[34]、Jaworski[21]和Kiera等[35]都认为，探究的取向和方式能促进教师教育工作者PKC的提升．

其他一些研究也讨论了中国数学教研员的挑战与发展．Wu Y等[36]指出了作为一个基于高效的数学教研员的挑战，探索了战胜这些挑战的策略．通过扩展Zaslavsky[25]的模型，黄荣金等[4]调查了教研员和教师如何通过课例研究的循环进行相互学习．

2.5 研究框架和研究问题

构建了两个框架：中学数学教研员PKC框架和中学数学教研员PKC发展模型．

中学数学教研员PKC框架：基于Ball[14]和Sutton等[28]的工作，结合中国教研员的特征[26，37]构建中学数学教研员的PKC框架：（1）学科专业知识；（2）学生学习知识；（3）教学能力；（4）教学评价知识和能力；（5）教学指导和科研能力；（6）培养骨干教师队伍，提供教育政策咨询．

中学数学教研员PKC发展模型：基于Jaworski[38]的观点和中国数学教研员专业发展的环境，构建中学数学教研员PKC发展模型：（1）自学；（2）参加培训活动；（3）公开课评价和反思；（4）指导教研活动；（5）主持教学研究项目；（6）撰写反思报告和教学材料．

利用上述两个框架，旨在回答以下问题：（1）中学数学教研员对自己PKC发展现状的自评、对PKC的期望的评价；（2）背景变量和中学数学教研员PKC发展状况之间的关系；（3）中学数学教研员对PKC发展途径的认识；（4）中学数学教研员PKC的期望．

3 研究方法

研究采用混合研究法．以中学数学教研员为研究对象，通过问卷搜集他们对自己PKC已有发展的评判（PKC的自评）、对理想中的PKC的评价（PKC的期望）以及PKC的有效发展途径的认识．

3.1 研究工具

研究问卷包括：（1）背景变量，如性别、指导学段、单位类型、学历、教学年限和专业技术职称；（2）中学数学教研员PKC的自评以及PKC的期望的评价量表（李克特五分量表）；（3）中学数学教研员对PKC发展的有效途径的评价量表（李克特五分量表）．除此之外，问卷还包括两个开放性的问题，要求参与者对PKC的维度以及有效发展PKC的途径进行补充．

在全国范围选择4位资深中学数学教研员（初高中各2名，省级1名、地市级2名、区县级1名），对问卷内容及表述进行修改，最后得到3个量表的克隆巴赫系数分别为0.93、0.96和0.83，说明问卷具有较好的信效度．

3.2 数据搜集

为了获得全国性样本，研究以省—地（市）—县（区）教研系统层级结构分布为依据，对被试采用层级分配的策略，由中国教育学会中学数学教学专业委员会会员单位组织问卷的发放和回收，收集到来自全国大部分省市自治区的549名中学数学教研员的数据．统计其基本信息见表1．

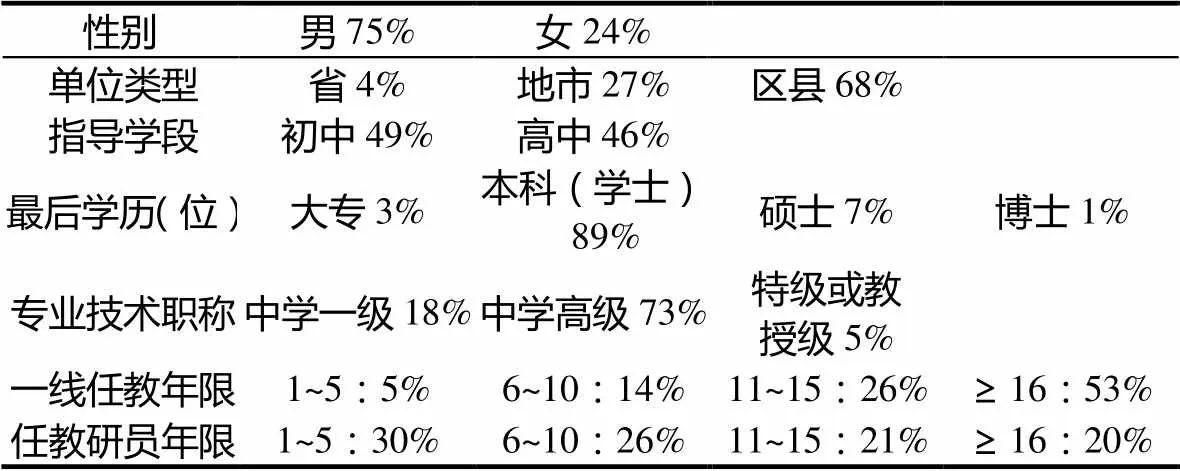
表1 被试的基本信息

注：某些变量百分数之和不足100%是因为数据的缺失

表1显示，被试分布比较理想，可以代表中国中学数学教研员的自然状态．

3.3 数据分析

研究通过量化分析和质性分析相结合的方法对问卷结果进行研究．教研员对PKC发展的自评被赋予1~5分，依次是十分不符合、不符合、不确定、符合、十分不符合；PKC的期望也被赋予1~5分，依次是十分不同意、不同、不确定、同意、十分同意．相关题目或子题目都进行了描述性的分析．T检验用来研究教研员对PKC的自评与PKC的期望的关系，ANOVA被用来检测被试基本信息与PKC的关系，因素分析用来对PKC的自评、PKC的期望、提高PKC的途径及其潜在结构的综合分析．在549位被试中，369位回答了开放性问题（67%），通过因素比较来分析数学教研员关于PKC及其发展途径的补充．

4 研究结果

4.1 对PKC的自评和对PKC的期望的评价

在回收的549份问卷中，对PKC的自评、对PKC的期望的评价回答率是96%，关于PKC发展途径的回答率是95%．教研员对PKC的自评、对PKC的期望的评价平均得分和标准差见表2．

4.1.1 PKC的自评

平均分大于4.20的有：能有效组织数学教研活动（16题，=4.34）；掌握评价课堂教学效果的各种方法，能给教师提出中肯的意见和有效的建议（15题，=4.26）；掌握学生的认知基础，并根据教材要求，有层次地设计问题，促进学生对相关概念的理解（9题，=4.25）；了解学生的常见概念错误，掌握一些有效方法来帮助学生纠正和避免这些错误（6题，=4.23）；能够理解教材的编写意图，并在教学设计中体现知识的发生、发展过程（8题，=4.23）；掌握数学课堂教学技巧，有效实施教学（10题，=4.23）；具有较强的与同事、学校沟通、协调的能力，以及组织能力（18题，=4.23）．这些结果表明，广大教研员认为自己在组织各种教研活动、和学校与教师沟通、理解教材、把握学生学习状况以及各种教学技巧的掌握等方面有能力，在评价课堂和给教师提出中肯意见上有自信．

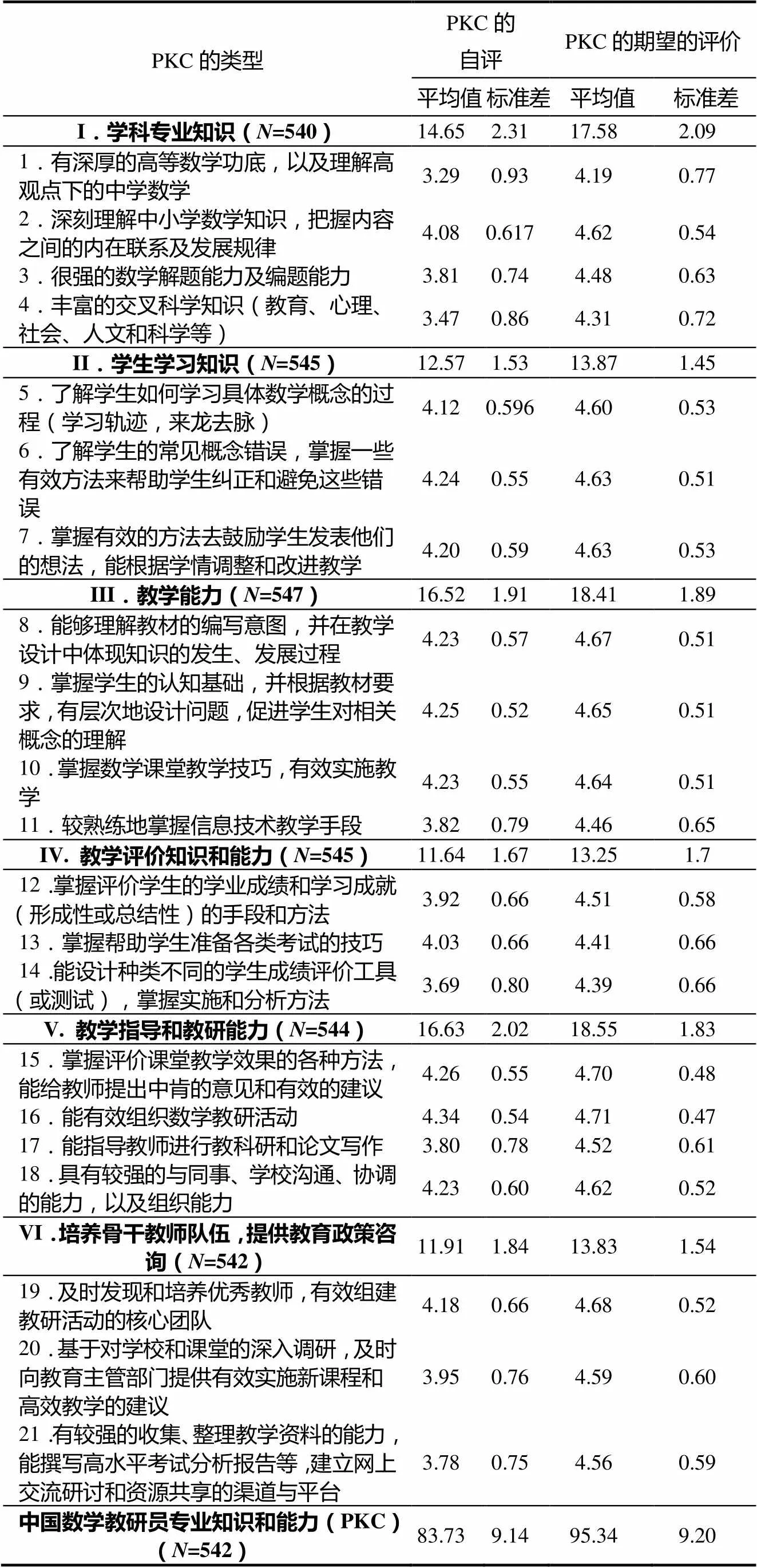
表2 PKC的自评和PKC的期望的评价平均分和标准差

另一方面，5个低分的题目（低于4分）是：有深厚的高等数学功底，以及理解高观点下的中学数学（1题，=3.29）；丰富的交叉科学知识（教育、心理、社会、人文和科学等）（4题，=3.47）；能设计种类不同的学生成绩评价工具（或测试），掌握实施和分析方法（14题，=3.69）；有较强的收集、整理教学资料的能力，能撰写高水平考试分析报告等，建立网上交流研讨和资源共享的渠道与平台（21题，=3.78）；能指导教师进行教科研和论文写作（17题，=3.80）．这一结果表明，广大教研员对高等数学知识以及理解高观点下的中学数学、评价和分析学生成绩、指导教学科研论文和论文写作以及建立网上研讨和资源共享的渠道和平台等方面不够自信，他们不认为自己有丰富的交叉学科知识．

4.1.2 PKC的期望

从被试给出的PKC的期望平均分可以看出，他们认为框架中如下6个方面相对重要：指导教学和教研活动（4.63）；培养骨干教师队伍，提供教育政策咨询（4.61）；学生学习知识（4.6）；教学能力（4.6）；学科和交叉学科知识（4.44）以及学生学习测评（4.41）．

4.1.3 PCK的自评与PKC的期望的比较

T检验显示，被试对PKC的自评与PKC的期望之间存在显著差异（=-25.701，=511，<0.01）．PKC的期望的平均分明显高于PKC自评的平均分．通过对具体题目的分析，发现在下面5个指标上的差距最大：有深厚的高等数学功底以及理解高观点下的中学数学（1题，0.80）；丰富的交叉科学知识（教育、心理、社会、人文和科学等)）（4题，0.89）；有较强的收集、整理教学资料的能力，能撰写高水平考试分析报告等，建立网上交流研讨和资源共享的渠道与平台（21题，0.78）；能指导教师进行教科研和论文写作（17题，0.72）；能设计种类不同的学生成绩评价工具（或测试），掌握实施和分析方法（14题，0.71）．该结果表明，参与回答问卷的教研员明确意识到自己需要在上述几个方面努力提高专业水平．

4.2 被试基本信息和PKC之间的关系

通过ANOVA分析了被试基本信息与其PKC的自评及PKC的期望之间的关系．结果显示：被试基本信息与PKC的期望之间没有明显的统计关系；女性（=82.41，=9.19）和男性（=84.19，=9.07；(521)=-1.912，=0.056；two-tailed）在PKC的自评上有略微的显著差异；教研员的不同任职年限对PKC的自评有统计意义上的差异（(3,511)=2.97，=0.03），事后比较（post-hoc）显示，第四组的平均分（=85.53，=9.99）明显高于第一组（=82.15，=8.34），其他组之间没有统计意义上的显著差异；专业技术职称对PKC的自评有<0.05的统计差异（(2,515)=10.20，=0.00)，事后比较显示，第一组（=82.04，=10.32）和第二组（=83.75，=8.36）的平均分明显不同于第三组的平均分（=91.16，=12.47），然而第一组和第二组的平均分没有显著差异．在<0.05的水平上，指导学段（初中和高中）、单位类型（省、市、区）和教学经验之间在统计意义上没有显著差异．

以上结果表明，在教研能力上，男性教研员比女性教研员更有自信；拥有特级头衔或担任教研员16年以上的数学教研员认为自己的教研能力更强．

4.3 PKC的补充维度

在369个回答了开放性问题的教研员中，有94%的人重复提到了问卷中包含的PKC的几个维度，同时还补充了PKC的5个方面：（1）对于教育和数学教学的激情、个人创造力、魅力以及人文关怀（17次，4.6%）；（2）理解最新的教育和教学理论，对课程标准有深刻的理解（教学目标，教与学的概念（16次，4.3%）；（3）理解教育政策（13次，3.5%）；（4）演讲和写作能力（8次，2.2%）；（5）专业道德（6次，1.6%）．事实上，（2）、（3）、（4）等方面非常接近6维模型要素，而且意义也是很明确的．

4.4 数学教研员对专业发展途径的看法

4.4.1 教研员心目中有效提升PKC的途径

对有效提升PKC途径的问卷进行内部信度检验，结果是0.83（Cronbach’s Alpha），超过通常接受的0.65．在549位回答者中，539人（98%）完成了问卷的所有题目．关于提升PKC有效途径的分析结果见表3．

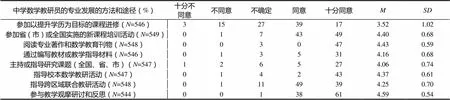
表3 数学教研员认为有效提升PKC的途径（N=539）

表3显示，被试认同以上途径对于他们专业发展的重要性（参加以提升学历为目标的课程进修例外）．这些途径的重要性依次是：参与教学观摩研讨和反思（=4.59）；阅读专业著作和数学教育刊物（=4.43）；参加省（市）或全国实施的新课程培训活动（=4.40）；指导校本数学教研活动（=4.37）；指导跨区域联合教研活动（=4.25）；通过编写教材或教学指导材料（=4.16）；主持或指导研究课题（=4.06）．

关于以提升学历为目标的课程进修，回答各有不同．在回答者中，18%认为这些课程没有用，56%认为有用，27%不确定，略多于一半的人认为这些课程是有效的，1/3左右的人不确定怎么给这一途径打分．这一结果显示，和其他的PKC提升途径相比，教研员对这些课程的质量和有效性的看法存在分歧，这与近些年国培、省培等培训项目授课中得到的反馈是一致的．

4.4.2 提升PKC途径的补充维度

通过开放性的问题，得到提升中学数学教研员PKC水平的4个新增途径：（1）参加为中学数学教研员定制的高端培训活动（市级的、省级的或者国家的）（124次，34%）；（2）参加跨地域（地区级或县级）的教研活动或者网上学习平台（76次，21%）；（3）向导师学习（特级教师或者熟悉6~12年级数学教学的大学教授）（25次，6.7%）；（4）通过现场参观和调研进行学习（23次，6%）．

4.5 中学数学教研员的PKC

4.5.1 对PKC的自评的因素分析

对教研员关于PKC自评的21个题目的回答进行了因素分析．这些数据用来进行因素分析的适合性（suitability）已经过评估，结果显示，21个题目中的任意一个和至少另外一个题目有0.3的相关性，所以因素分析具有合理性．KMO值是0.93，高于普遍被接受的0.6．Bartlett’s test of sphericity达到统计显著（=6051.37，<0.05），支持了相关矩阵的因素分析．主成分分析，通过varimax and oblimin rotations分析表明，4个成分特征值超过1，分别解释了差异的43.3%、8%、6%、6%．基于模式矩阵，PKC问卷设计中类别的关系和检测到的因素成分如表4所示．

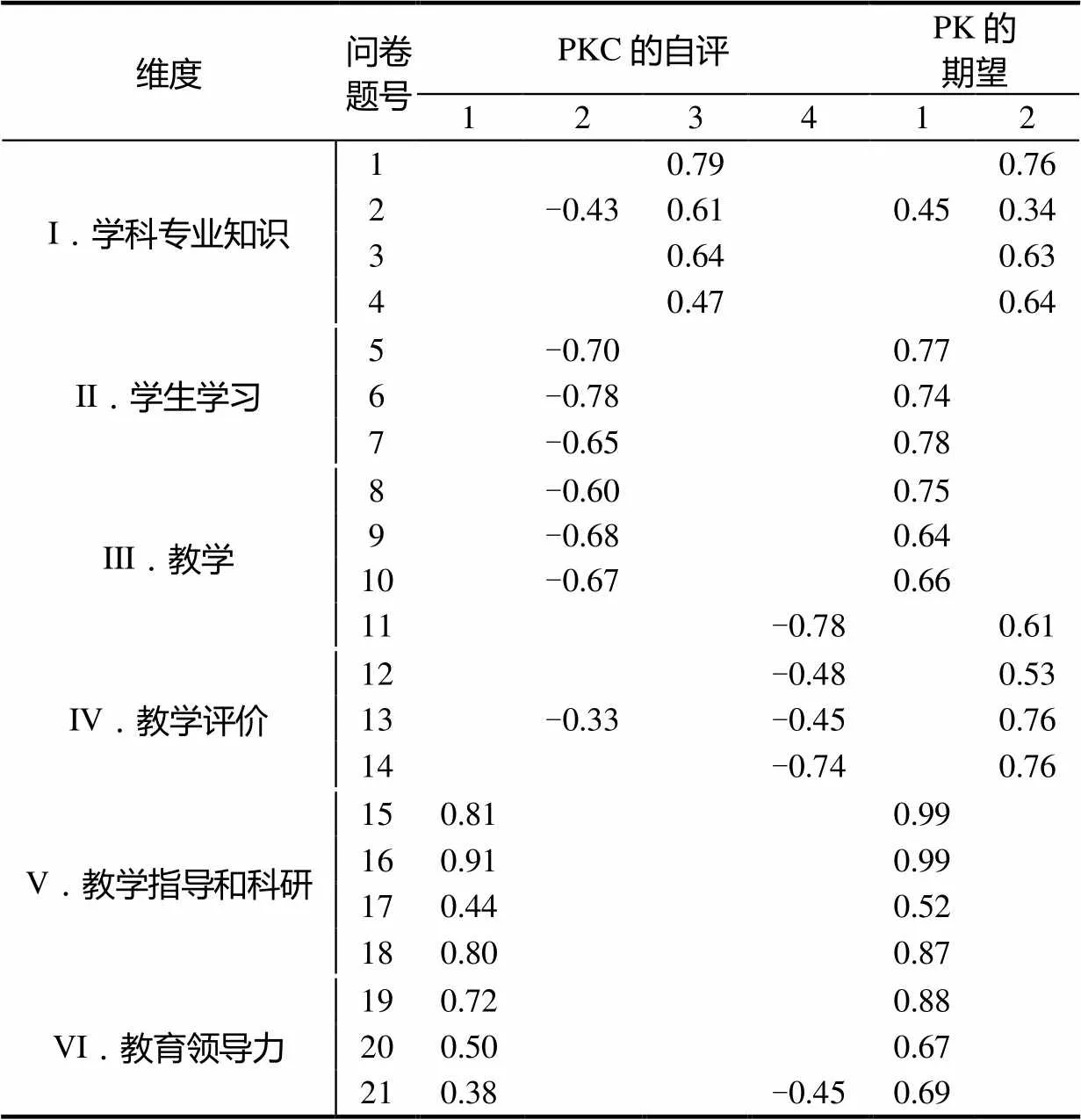
表4 PKC的自评和PKC的期望的因子载荷

数据显示，教研员指导能力和领导力是一个主要成分，贡献了PKC差异的43%；与此同时，关于学生学习和教师教学的知识贡献了PKC差异的8%；学科和跨学科知识、学生评价相关知识和信息技术教学手段的使用分别贡献了PKC差异的6%．总的来说，中学数学教研员回答关于PKC自评的问卷显示了潜在的4个主要因素，而且这些因素具有内部一致性．

4.5.2 对PKC的期望的分析

研究对21个关于PKC的期望的题目的回答进行了因素分析．主成分分析表明，两个成分的特征值超过1，解释了PKC的期望的差异的58.9%和5.7%．进一步的，模式矩阵表明，成分1包括关于学生学习和教师教学的知识（题目5~10）、指导能力和领导力（题目15~22），贡献了PKC的期望的差异的59%．成分2包括学科知识和跨学科知识（题1~4）、关于学生学习评价和信息技术手段的使用（题目11~14）（见表3），仅仅贡献了PKC的期望的差异的6%．总体而言，中学数学教研员理想中的PKC结构有两个突出因素，而且它们之间有内部一致性．

4.5.3 发展PKC的有效途径

关于发展PKC有效途径的问卷中的8个题目的评价再次确认了教研员PKC的因素分析具有统计显著性（=0.86，（=1529.85，<0.05)．然而，所有的题目只能够归因于同一个内在结构因素，它对有效专业发展途径的贡献是49%．结果表明，教研员专业发展的有效途径有一个整体结构，所有这些途径综合起来影响数学教研员的PKC的发展（题目载荷为0.46 ~0.8）．

4.5.4 小 结

通过对PKC的自评和PKC的期望中呈现的因素进行比较，结果表明：指导能力和领导力与关于学生学习和教师教学的知识可以合并为一个因素，贡献了PKC的期望的差异的约60%；学科和跨学科知识与学生学习评价知识和信息技术手段的应用可以整合为另外一个因素，解释了PKC的期望的差异的6%．教研员认为，提高PKC的有效途径（除了参加以学历为目的的培训课程，最低载荷（0.46）与提升PKC中主要因素的水平息息相关：指导力和领导力、教与学．

5 结论与讨论

5.1 结 论

5.1.1 中学数学教研员PKC的期望

研究旨在填补基于实证的中国中学数学教研员专业知识、能力及其发展的模型的空白．通过量化和质性的分析，提出中学数学教研员PKC的六维模型如下：（1）学科和跨学科专业知识；（2）学生学习；（3）教学能力；（4）教学评价知识和能力；（5）教学指导和教研能力；（6）培养骨干教师队伍，提供教育政策咨询．

质性数据分析对该模型进行了补充，增加了交叉学科知识，例如教育和教学理论、对课程标准的深入理解；人文方面的价值观，例如对教育的热情、创造力、个人魅力以及专业道德．

通过因素分析对模型进行了修正，将6个维度分为两个主要部分：第一部分是教、学、指导能力和领导力，第二部分是关于数学、交叉学科、学生评价和信息技术手段的运用的知识．

5.1.2 提高PKC的有效途径

关于提高PKC的有效途径，被试在整体上认同从阅读、实践、指导和反思中学习的重要性．同时，他们强调通过丰富的活动来学习，包括：（1）学习专业书籍和材料；（2）参与具体的培训课程；（3）观察和反思公开课；（4）指导教研活动和主持研究课题；（5）与专家交流；（6）跨地域的联合教研活动，包括现场的和网上的．

5.2 讨 论

5.2.1 丰富了对中学数学教研员PKC的理解

研究论证了中学数学教研员PKC六维模型的合理性，当然该模型还可以作进一步的修订．通过增添一个关于一般素养的维度，包括个人魅力和道德，该模型拓展了对中学数学教研员PKC的认识．例如，在Zaslavsky and Leikin的模型中[22]，两个主要的部分是组织数学教师的学习和对数学教师有敏感度．该研究提出了在中国的环境下，组织教师学习这一维度具体需要的PKC包括课堂观察、课堂评价及指导教研活动，它们都是教研活动至关重要的部分[10]．研究具体化并拓展了已有文献中关于教研员PKC的8个维度[28]．研究表明，PKC的6个维度可分为两类，其中一类贡献了PKC差异的60%．这一发现可以帮助找出在不同文化下有效提升PKC的途径，例如在学校和跨地域基础上的课堂观察、点评、反思和改进，这种途径也可以被其他的教师教育系统所采纳．

5.2.2 关于培养高水平中学数学教研员的思考

如何培养高水平的教师教育工作者，在国际上仍是一个需要探索的开放性问题[32]．在中国，教研系统和相关的职称晋升系统[11]提供了筛选和培养数学教研员的基础．PKC的主要部分（教、学、指导能力和领导力）和教研员对提升PKC有效途径的看法具有高度一致的相关性，这表明，中国数学教研员在自己的实际工作中，高度重视根据工作需要加强重要知识的学习，能在工作实践中不断提高自己的专业能力．研究中发现的一些中学数学教研员专业发展途径，可以为其他教师教育系统在培养教师教育工作者时提供借鉴．尽管作为一个反思的学习者，并通过实践进行学习对教研员的专业发展非常重要[24~25，37]，但仍不清楚中学数学教研员该怎样成为反思的实践者．令人欣慰的是，研究得到了一些提升反思能力的具体途径，例如通过指导不同层次的跨地域的教研活动，并对这些活动进行反思．因此，研究补充了关于非英语国家的基于实践的教师教育工作者的文献，并为全球的教师教育工作者的发展提供了建议．

5.2.3 研究不足和建议

首先，在样本量上，尽管已经尽最大努力得到了一个大样本，并在样本分布上有较为周密的设计，但考虑到中国数学教研员的庞大数量[12]，把研究结论进行普遍性推广仍需谨慎．同时，只有4%的被试指出了PKC的附加维度，这些维度需要进一步的检验．

其次，研究没有直接测量中学数学教研员的PKC．因此，今后的研究有必要像测试数学教学知识一样[14]，设计直接测量数学教研员PKC的工具，并探索教研员专业成长的个案．

[1] Lewis C, Lee C.[M]. International Handbook of Teacher Quality and Policy, New York, NY: Routledge, 2017.

[2] Huang R, Shimizu Y. Improving Teaching, Developing Teachers and Teacher Educators, and Linking Theory and Practice through Lesson Study in Mathematics: An International Perspective [J]., 2016, 48(4): 393-409.

[3] Chokshi S, Fernandez C. Challenges to Importing Japanese Lesson Study: Concerns, Misconceptions, and Nuances [J]., 2004, 85(7): 520-525.

[4] Huang R, Su H, Xu S. Developing Teachers’ and Teaching Researchers’ Professional Competence in Mathematics through Chinese Lesson Study [J]., 2014, 46(2): 239-251.

[5] Huang R, Gong Z, Han X. Implementing Mathematics Teaching that Promotes Students’ Understanding through Theory-driven Lesson Study [J]., 2016, 48(4): 425-439.

[6] Takahashi A. The Role of the Knowledgeable Other in Lesson Study: Examining the Final Comments of Experienced Lesson Study Practitioners [J]., 2014, 16(1): 4-12.

[7] Takahashi A, McDougal T. Collaborative Lesson Research: Maximizing the Impact of Lesson Study [J]., 2016, 48(4): 513526.

[8] Lewis C. How Does Lesson Study Improve Mathematics Instruction [J]., 2016, 48(4): 571-580.

[9] Chen X, Yang F. Chinese Teachers’ Reconstruction of the Curriculum Reform through Lesson Study [J]., 2013, 2(3): 218-236.

[10]  Huang R, Han X. Developing Mathematics Teachers’ Competence through Parallel Lesson Study [J]., 2015, 4(2): 100-117.

[11]  Huang R, Ye L, Prince K.[M]. Professional Development of Mathematics Teachers-An Asian Perspective, Springer Singapore, 2017: 17-31.

[12]  Wang J.[M]. Gale Asia Cengage Learning, 2013.

[13]  Gu F, Gu L. Characterizing Mathematics Teaching Research Specialists’ Mentoring in the Context of Chinese Lesson Study [J]., 2016, 48(4): 441-454.

[14]  Loewenberg Ball D, Thames M H, Phelps G. Content Knowledge for Teaching: What Makes It Special [J]., 2008, 59(5): 389-407.

[15]  Shulman L S. Those Who Understand: Knowledge Growth in Teaching [J].1986, 15(2): 4-14.

[16]  Tatto M T, Peck R, Schwille J, et al.[M]. International Association for the Evaluation of Educational Achievement, Herengracht 487, Amsterdam, 1017 BT, The Netherlands, 2012.

[17]  Ma L.[M]. Mahwah, NJ: Lawrence Erlbaum Associates, 1999.

[18]  Wu Y, Huang R.[M]. How Chinese Teachers Acquire and Improve Mathematics Knowledge for Teaching, Rotterdan: Sense, 2017.

[19]  Beswick K, Goos M, Chapman O.[C]. Proceedings of the 38th Conference of the International Group for the Psychology of Mathematics Education and the 36th Conference of the North American Chapter of the Psychology of Mathematics Education, Vancouver, Canada: PME. 2014: 254.

[20]  Jaworski B.[C]. Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education, 2004, (1): 17-36.

[21]  Zaslavsky O, Leikin R. Professional Development of Mathematics Teacher Educators: Growth through Practice [J]., 2004, 7(1): 5-32.

[22]  Perks P, Prestage S. Tools for Learning about Teaching and Learning [J]., 2008, (4): 265-280.

[23]  Smith K. Teacher Educators’ Expertise: What Do Novice Teachers and Teacher Educators Say [J]., 2005, 21(2): 177-192.

[24]  Schön D A.[M]. Oxford: Jossey-Bass, 1987.

[25]  Zaslavsky O. Meeting the Challenges of Mathematics Teacher Education through Design and Use of Tasks that Facilitate Teacher Learning [J]., 2008, (4): 93-114.

[26]  Even R. Integrating Knowledge and Practice at MANOR in the Development of Providers of Professional Development for Teachers [J]., 2005, 8(4): 343-357.

[27]  Huang R, Xu S, Su H, et al.[C]. Paper presented at 12th International Conference on Mathematics Education, Seoul Korea, 2012.

[28]  Sutton J T, Burroughs E A, Yopp D A. Coaching Knowledge: Domains and Definitions [J]., 2011, 13(2): 12-20.

[29] 中国教育学会中学数学教学专业委员会．中学数学教研工作指导意见（地（市）、区（县）级，试行稿）[J]．中国数学教育，2014，（9）：61-64．

[30] 何晓波．教研员核心能力系统元素、特征及发展动力探析[J]．教育导刊，2013，（10）：38-40．

[31] 罗滨．教研员核心素养：教研转型背景下的新修炼[J]．中小学管理，2016，（4）：15-17．

[32]  Archibald S, Coggshall J G, Croft A, et al.[M]. National Comprehensive Center for Teacher Quality, 2011.

[33]  Campbell P F, Malkus N N. The Mathematical Knowledge and Beliefs of Elementary Mathematics Specialist-coaches [J]., 2014, 46(2): 213-225.

[34]  Cochran-Smith M, Lytle S L. Relationships of Knowledge and Practice: Teacher Learning in Communities Review of Research in Education [J]., 1999, (1): 24.

[35]  Kieran C, Krainer K, Shaughnessy J M.[M]. Third International Handbook of Mathematics Education, Springer New York, 2012: 361-392.

[36]  Wu Y, Hwang S, Cai J. Being a Mathematics Teacher Educator in China: Challenges and Strategic Responses [J]., 2016: 1-20.

[37]  Jaworski B.[M]. International Handbook of Mathematics Teacher Education: The Mathematics Teacher Educator as a Developing Professional, Rotterdam: Sense Publishers, 2008: 335-361.

Perceived Professional Knowledge and Competence of Mathematics Specialists and Its Development in China

ZHANG Jian-yue1, HUANG Rong-jin2, ZHAO Wen-jun3, MO Ya-chi3, WU Zeng-sheng4, ZHOU Yuan-fang5

(1. People’s Educational Press, Beijing 100081, China;2. Mathematics Department, Middle Tennessee State University, USA;3. Education College, The University of Hong Kong, Hong Kong SAR, China;4. Xianju Teaching Research Office, Zhejiang Taizhou 317300, China;5. Hubei Teaching Research Office, Hubei Wuhan 430071, China)

The purpose of this study is to explore what professional knowledge and competence (PKC) that knowledgeable others, namely, mathematics teaching research specialists (MTRS) in China, need to know, and how they may develop their PKC. This study adopts mixed methods. A survey on PKC with 549 MTRS is utilized to examine MTRS’ perceived held and ideal PKC and perceived effective ways of developing their PKC. The responses to the open-ended questions on the survey were used to identify additional dimensions of PKC and ways of developing PKC. Multiple techniques of quantitative data analysis were employed to feature the characteristics of PKC and structure of the survey, and the relationship between background variables and perception of PKC. Collectively, this study paints a rich and comprehensive picture about Chinese knowledgeable others’ knowledge and competence, and its development. The data analysis reveals that the participants appreciated the six-dimension model of MTRS’ PKC. They were confident with their PKC in general, but varied in different aspects. The factor analysis showed the six-dimension model could be further clustered into two components: (i) knowledge about mathematics teaching and learning and competence in mentoring and educational leadership, and (ii) knowledge about content, assessing student learning, and use of technology. The participants perceived their learning through multiple ways including: learning through reading, attending specific training programs, attending and mentoring teaching research activities both school-based and across-regions, observing and debriefing lessons, sharing within online learning communities.

Chinese lesson study; teaching research activity; mathematics teaching research specialists (MTRS); professional knowledge and competence (PKC); professional development

[责任编校：陈隽]

G633.6

A

1004–9894（2017）04–0001–07

2017–07–16

章建跃（1958—），男，浙江金华人，博士，编审，中国教育学会中学数学教学专业委员会理事长，主要从事数学课程、教材、教法研究．