中学数学微实验的设计原则及开发途径——基于HP Prime平台

张志勇



中学数学微实验的设计原则及开发途径——基于HP Prime平台

张志勇

（江苏省常州市第五中学，江苏常州 213001）

由知能视角下的教学走向核心素养的有意识培育，离不开数学实验的土壤．作为一种以实际操作为特征的数学验证、理解或探究性活动，数学微实验（类似于片段式实验）以移动可视技术为工具，支持随时随地的实验和分享，往往聚焦于某个数学知识点（重点、难点、疑点）或教学环节，强调实验进程的短（实验时间）、平（操作简易）、快（实验见效），为学习者提供碎片化、移动化的探究体验的同时，可以方便地嵌入、融合到原有的教学流程中．从完整的教学链出发，可将数学微实验细分为情境创设、现象挖掘、原理探究、方法发现、解释构造、拓展推广等3类6种实验．Hp prime图形计算器具有视觉化、操控化、瞬时化特点和手持优势，借助这一平台，以可操作性、过程性、再创造性、拓展性为原则，设计并开发微实验资源，或深入教材挖掘素材，或立足史实追本溯源，或命题推广寻求解释，或归纳演绎流程再造，……，可推动数学微实验在课堂教学中的常态化实施．

数学微实验；图形计算器；移动实验室；核心素养

1 研究背景

长期以来，人们对数学的认识就是概念、定理、公式和解题，这固然可归咎于数学自身具有的形式化抽象特征，但当下重结果轻过程、重知识轻能力、重训练轻理解……的知识教学却也责无旁贷．如果只是掌握知识的结果，而不追问这些知识的结果从何而来又向何而去；如果只是埋首于题海中刷题而不理解数学的本源性问题[1]；那么学生从哪里抽象、拿什么建模、凭什么推理？

由知能视角下的数学教学走向核心素养的有意识培育，需要摈弃以往教学中过于强调形式化的逻辑推导和形式化结果的弊端，重视数学发现过程的展示、数学学习活动的亲身体验和数学直观性背景的创设；在问题的发现、方法的形成、知识体系的构建过程中，让学生感悟蕴含其中的数学思想和数学方法，进而认识数学本质[2]．而这样的教学构想离不开数学实验的土壤，通过实验手段来学习、验证和发展数学，可以将抽象的结论寓于其中，使学生经历一个从具体到抽象的过程，从而见到数学的全貌、体会数学的全过程；而从直观、想象到发现、猜想，也能保证原先枯燥无味的数学公式、数学概念、数学定理变得鲜活起来．

随着遍地开花的高校数学实验教学中心的逐步建设，肇始于高等教育的数学实验已然成为数学教学方法中必不可少的元素．研究者采用不同的技术平台（Mathematica、Matlab、图形计算器等），或采用课堂教学与数学实验交替进行的方式，或融数学实验于日常数学课程中，构建了基于数学基础实验、工程应用、创新活动的3个层面多个模块的实验教学体系[3]，在实践应用基础上不断探讨数学实验于数学教育的作用及价值：数学实验改变了数学只用纸笔进行研究的传统方式；借助计算机和数学软件能理解抽象的数学理论、自主探索和研究数学应用问题；帮助学生初步实践利用数学知识和方法去分析和解决问题的全过程，培养学生自主获取各种新知识的能力[3]；学生应用数学解决实际问题的最佳途径，培养创新型、应用型和复合型人才的最佳载体[4]；促进学生认知发展的有效途径，对教学过程完善性的必要补充，为课程资源开发提供了源头活水[1]；将过程与结果、操作与思维、实验与论证、证伪与证实有机融合，实现了静态数学观与动态数学观的融通，使得数学教学变得完整而有活力[5]．开展数学实验离不开现代教育技术的助力，特别地对于图形计算器，研究者提出需要选择适当的时机、恰当的度，使用时机的把握要与学生的发展水平相适应，使用方式的选择要有利于创建新型的教学结构，使用目标的确定要以培养学生的数学思维能力为核心[6]；而相应的教学策略则包括掌握使用要点、创设活动环境、加强多元表征、利用计算统计功能等[7]．而具体到中学阶段开展数学实验，调查研究表明，大多数教师认为非常有必要，但实践中却开展较少，究其原因主要在于缺乏数学实验课程资源的支持；无论是教材、教学还是教师，让数学实验教学真正落地，从观念存在变为有助于培养学生创新意识的现实，还需要深入的研究和探讨，聚焦数学主题的专题性实验（大实验）固然必要，但穿插于数学课堂教学中的片段式实验（小实验）却更实际[8]，目前关于中学数学微实验的内涵、设计原则和开发途径的探讨和研究尚不多见．

2 数学微实验的涵义认识

数学实验是一种以实际操作为特征的数学验证、理解或探究活动．它强调的是学生的动手实践，在算一算、画一画、量一量中获得活动体验；强调的是不将现成结论直接抛给学生，而是根据数学思想发展脉络创造问题情境；强调的是“做”中理解数学、发现数学，从直观、想象到猜想、发现，亲历数学知识的建构过程，而不是简单的应用数学解决问题；也就是在“做”数学的过程中丰富感知，在直观感知的基础上建立表象，在表象提取与运用中发展想象[9]．简而言之，数学实验始于基本活动经验的积累，终于数学核心素养的发展．

区别于普通数学实验而言，数学微实验（类似于片段式实验）更多地强调实验进程的短（实验时间）、平（操作简易）、快（实验见效），它以移动可视技术为工具，支持随时随地的实验和分享，往往聚焦于某个数学知识点（重点、难点、疑点）或教学环节，为学习者提供碎片化、移动化的探究体验的同时，可以方便地嵌入、融合到原有的教学流程中．当然，微实验也注重知识发生、发展过程的合理再现，注重学生在“做”中亲历数学概念、规则的形成过程，注重通过动作思维和逻辑思维感悟知识发生过程、理解知识结果．于是，所谓数学微实验，是学习者在数学思维活动参与下，借助移动可视技术，模拟地创设可观察的数学对象或问题情境，在数学化操作中产生归纳假设，在分析、验证、猜想中形成认知体验，从而实现在做（建构）数学中学（理解）数学、用（解释）数学的一种移动式探究性学习活动．

考虑到数学微实验以“短小精悍”为特色，往往可以嵌入到传统的教学流程中应用，而完整的教学链又应当包括3个阶段：怎么来的？是什么？怎么去的？[1]因此将数学微实验细分为以下3类：一是情境创设、现象挖掘类实验，用以凸显数学知识是“怎么来的”，包括所学习知识的缘由、新旧知识间的关联和冲突等，此类实验更多的指向学生的数学理解，多以教师演示的方式呈现，重在启发学生思考为什么要学习新知识；二是原理探究、方法发现类实验，侧重于描述知识“是什么”，此类实验多以探索性形式呈现，通过观察、测量、计算等活动认识不同水平条件下的数学本质，通过归纳、类比、概括等思维方式发现数学规律，从而达到建构数学认知结构的目的；三是解释构造、拓展推广类实验，体现知识是“怎么去的”，用以启发学生思考新知识会向什么方向发展，在这个知识基础上会再生成什么新的知识，多以验证性实验的形式呈现，用以帮助学生对知识结果的理解，包括利用知识解决数学本身的问题和解决一些现实生活中的问题．

3 Hp Prime平台简介

作为一款移动手持终端，HP Prime图形计算器集“数、形、表”于一屏，3种视图模式（符号视图Symb、绘图视图Plot、数字视图Num）的设计，能够轻松实现数学概念或对象的多元联系表征；18个内置应用APP、400多种操作命令，为数学实验的开展提供演示、验证和探究3种水平的支持，可以生动地展示数学对象的动态变化过程，实现动态与静态间的适时切换，显现代数、几何、数据、算法等不同数学分支的真正融合；内嵌的符号代数系统，使形式化的符号不再成为开展数学实验的障碍，数学推导（因式分解、微积分运算等）在计算器上也可以顺畅实现；从而能够深入数学学科内部、帮助学生洞察数学本质，满足学生在更高抽象层次上进行思考与探究的需求．

如果说HP Prime的视觉化、操控化、瞬时化特点，可以有效支持数学微实验开展需求的话；那么其手持优势（支持随时随地“学”、“做”、“用”数学），则是移动实验学习的重要支撑（其模拟软件可在各类移动终端设备上免费安装使用，确保移动可视化实验的顺利开展）．需要提及的是，HP Prime配以Connkit课堂管理系统、无线模块，可以搭建课堂无线环境形成e-数学实验室，实现课堂动态管理、师生的即时顺畅互动和自定义APP的及时分享．当然，最为重要的还是HP Prime易于交到学生手中，可以成为学习和解决数学问题的强有力的工具，保证“使用技术学习和研究数学”成为可能：通过对由“静”到“动”、从“微观”到“宏观”的知识形成过程的观察和思考，不仅看到数学外在形式的“美”，还可感受到内在实质的“真”；超越传统意义上纸笔学习数学的窠臼，在真实体验指尖上的美妙数学和探究乐趣之余，实现“人人通过微实验学习数学”．

4 数学微实验的设计原则

数学微实验目标定位在于：亲身操作中获得“关键性事件”的学习体验，经验积累中促成思维深化，知识获取中提升数学索养……如何达成？需要遵循以下一些设计原则．

4.1 可操作原则

数学微实验强调短、平、快，实践性和操作性是它的外部特征[5]，学生的学习体验获得依赖于其亲身操作和观察发现，可谓“实验不动手，体验不会有；操作不顺畅，价值难保障”，于是可操作性便成为实验内容选取和实验资源创设过程中的首要原则．

可操作性首先要求对数学内容进行实验法加工，并非所有的数学内容都适合探究，教材中也并没有现成的实验资源，需要教师下力气提炼教学内容，透视知识背后的实验成分，化数学内容的学术形态为实验形态，创设利于学生“再创造”的实验情境；其次要求实验内容与操作工具的互融共通，好的教学构想离开技术上的方便快捷实现也是枉然，创设“多元联系表征”的学习情境，把教学中抽象、难以理解的知识点以形象、直观的方式展现在学生面前，可以实现信息在外部世界和学生大脑之间的“自由穿梭”，达成实验与归纳、演绎与推理的平衡与统一．

4.2 过程性原则

数学微实验重视基本活动经验的积累，数学活动经验的形成和发展主要来自于过程性知识的习得．于是，实验中需要注重学生在“做”中亲历数学概念、数学规则的形成过程，重视学生对知识产生和发展的体验，通过动作思维和逻辑思维来感悟知识发生过程、理解知识结果、明晰知识发生发展的来龙去脉并形成直接经验[5]．

正如“精彩源自细节，过程成就素养”，过程性原则强调的是寓理于行，操作与思考并行，在“做”的过程中积淀、在“思”的过程中升化，不愤不启不悱不发；过程性原则追求的是水到渠成，重要的不是结果性知识的获得，也不是应用数学来简单的解决问题，而是知识背后的发现和探索过程的不断经历和体验，是结果与过程的融通．

4.3 再创造原则

根据数学思想发展脉络，选取适当的对象创造问题情境，安排适当的活动让学生获得感性认识，亲历数学知识的建构过程，从而理解数学概念、提炼数学思想、发现数学规律，数学微实验所倡导的正是弗赖登塔尔所说的“数学再创造”．

再创造首先意味着不是简单地将概念、法则、定理“告诉”学生，而是创设适合的条件、提供更多的作为知识载体的具体情境，让学生在实践活动中自己再创造出各种数学知识，正如学游泳、骑自行车一样，实践才能出真知，它强调的不是“知其然”而是“何以知其所以然”；其次再创造的着眼点是“再”，并非要求学生发现前人所没有发现的数学结论，而是把数学的学术形态转化为学生易于接受的实验形态，其教学价值在于养成具体环境中用数学的习惯，在于数学思维水平的提升．

4.4 拓展性原则

通过实验活动促进学生思维的发展是数学实验的核心和最终归宿，在一个数学实验中，观察与分析交织，抽象思维与形象思维并存，从实验前的猜想，实验中的思考，以及实验后的总结，都是发展学生思维的优良环境，同时也为培养学生创造思维力提供空间．

一个好的数学实验不会仅停留在动手操作层面，它必然是实验与论证的统一，既具有帮助学生理解、领悟数学知识的目标追求，更具有为数学思维奠基、促进学科素养形成的价值取向．拓展性也意味着动态、包容和可持续，微实验设计更多地指向教学片断，多个微实验进行有效整合可形成一完整的数学实验系列或体系；在实验设计和实施过程中，对实验设计的动态检测和成果评价反馈的逐步完善，亦是拓展性的一种体现；况且学生也可仿照流程自主设计实验，探索相近的或相似的数学结论．

5 数学微实验的开发途径

数学实验材料本身属于内隐性课程资源，如前所述并非所有的数学内容都适合探究，教材中也并没有现成的实验资源，开发这些资源需要教师对数学知识有深刻的理解，尤其是知识的产生、知识之间的联系、知识中包含的数学思想方法；需要教师有敏锐的洞察力和创造力，能透视作为结果性知识背后的实验成分，对其进行教学法层面的再加工，形成实验设计[1]．

5.1 情境创设和现象挖掘类实验的开发设计

认知发展理论表明，真正的学习不是个体对外部知识的简单接受，而是在活动中不断同化、顺应的结果，于是可以从知识产生的过程和在知识产生过程中出现的曲折来着手开发实验．

对于情境创设实验而言，重要的是引发学生原有的数学认知结构与新学习内容之间的认知冲突，使得学习者在心理上对新知识产生学习需要．可以从教材中的章节引言中寻求素材，围绕为什么学、学什么、怎么学等开发案例，如矩阵与变换的教学中，可以构建矩阵（代数范畴）与变换（几何内容）的联系通道，拖动图1中的变量滑动条出现图形变换效果，而打开图2中相应点的属性自可揭开谜底[10]；也可基于数学史的视角进行数学内容的实验设计，如从赵爽弦图、帕普斯半圆模型出发引出均值不等式，自有事半功倍之效．现象挖掘类实验，则着眼于从若干具体事例中发现共性规律、寻求数学解释，体现“由数学看现实，由现实想数学”．开发此类实验，重要的是多个现象的同时呈现，而这正是HP Prime最容易实现的，如当学生观察到多个方程（、、、等）的图象后，当他们归纳发现所有直线都过同一点（区别仅在于直线的斜率不一致）时，点斜式方程便自然可以“呼之欲出”．

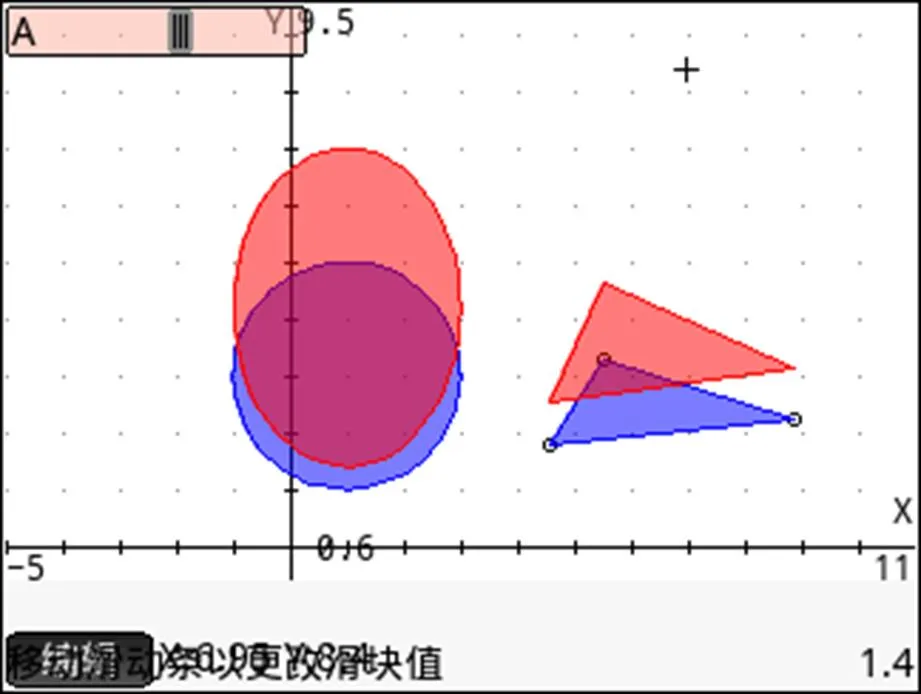
图1 图形计算器输出（一）

图2 图形计算器输出（二）

5.2 原理探究和方法发现类实验的开发设计

数学是高度抽象的形式化的思想材料，真实的内容和抽象的意义往往隐藏在符号形式的背后，这就要求能透过现象看本质，从具体现象中抽象概括出数学本质的东西．如何帮助学生在自己的头脑里建立和发展数学认知结构，这就需要开发原理探究、方法发现类实验，如果说前者立足于运用数学知识去发现、探究新的原理、规律、公式的话，那么后者则着眼于将现实生活中蕴含的与数量和图形有关的问题抽象成数学问题．

开发设计此类实验，可以从抽象内容的直观表示入手，如让图3所示的不等式“说话”，通过解析式的不断修改，引发可行域的即时变化，使得抽象的不等式组与具体直观的几何图形间形成鲜活的联系，而丰富的案例（每一次修改即是一个案例）也为规律（不等式对应的区域）的探寻提供了直接的通道．对于数学规则、定理的学习，可使用流程再造的方式设计实验，其做法就是充分利用HP Prime的CAS功能，如学习“两角和与差的余弦公式”时，可如图4输入

、，

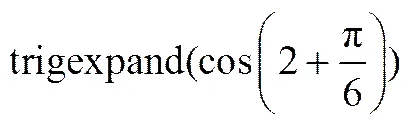
可以验证前面的猜想，事实上图形计算器本身就是数学，通过实验设计可实现“向技术学习数学”，做过去课堂中完全做不到的事情．

图3 图形计算器输出（三）

图4 图形计算器输出（四）

5.3 解释构造和拓展推广类实验的开发设计

知识的价值不在于占有而在于应用，于是数学实验的价值理应体现在由直观的“做”转型到有意识的“用”，以此发展学生的数学应用意识，回归素养为重的常识．

解释构造类实验侧重于寻求“问题空间”的另类数学解释，即在架设新内容与既有的知识间的联系通道的同时，构建更加完善的知识网络体系．如学习完函数的奇偶性后，可应用奇偶函数的概念来构造分段函数，假定（基本函数），那么、分别对应着奇、偶函数，进入绘图视图可以清晰地发现其图象的对称性，而进入CAS系统查看解析式，恰可以从解析式的构造中看出图象对称性的“端倪”，最关键的是这样的场景恰可以通过修改基本函数的表达式得到复制和再现．

拓展推广类实验则多体现在从课本内到课本外的延展学习上，如一些圆锥曲线命题的探源推广研究，在限定或放宽某些条件下，通过对其结论的变与不变性的探索和建构，从而得出更具有一般意义下的规律和法则；当然也有一些现实生活中的问题解决，从数学模型的建立到性能的预测，从算法的设计到规律的探求等，都可将HP Prime作为理想的认知工具，看以往只能“想象”的数学，“做”以往不能做的数学，为学生学习数学的形式和空间带来新的气象和新的内涵．

围绕微实验设计原则，从微实验的分类入手，或深入教材挖掘素材，或立足史实追本溯源，或命题推广寻求解释，或归纳演绎流程再造，不同类型的微实验有着不一样的开发路径，在回应当下实验资源匮乏的实践需求的同时，也为数学微实验在课堂教学中实现常态化实施提供有力保障．

6 讨论与结论

既往的数学实验的研究多从宏观层面探讨数学实验的教育价值、方法涵义、实施路径，距离课堂教学的日常较远．而从微观立足，则可回应数学实验常态化教学实施需求．数学微实验（类似于片段式实验）更多地强调实验进程的短（实验时间）、平（操作简易）、快（实验见效），以移动可视技术为工具，支持随时随地的实验和分享，往往聚焦于某个数学知识点（重点难点疑点）或教学环节，为学习者提供碎片化、移动化的探究体验的同时，可以方便地嵌入、融合到原有的教学流程中．

可以说微实验的价值即在于“微”，因为“微”而可以随时随地的实验和分享，因为“微”而可以与现有的教学环节互融共通．当然数学实验走进课堂带来的是愈加复杂的教学境脉，如何在“做”的过程中引导学生“想”，如何将微实验教学契入融通于既有的教学流程中，包括具体的实施措施和评价标准等的制定等，还存在诸多的困惑，需要更加微观深入的研究和探讨．但数学微实验就是落细、落实数学核心素养培育的不可或缺的“桨”，基于HP prime平台，开发、设计、实施数学微实验，在亲历问题的发现、方法的形成、知识体系的构建过程中，领悟数学问题的探究方法，由“学会”变成“会学”，需要有数学教育专家的引领、数学教研工作者的助推，更需要广大一线数学教师的自身实践．

微实验的设计原则和开发途径包括：借助Hp prime平台，以可操作、过程性、再创造、拓展性为原则，设计并开发情境创设、现象挖掘、原理探究、方法发现、解释构造、拓展推广等3类6种微实验．

[1] 喻平．数学实验的教育价值[J]．江苏教育（中学教学），2016，（3）：19-21．

[2] 周玮．融数学实验于高职数学教学的实践与研究[J]．数学教育学报，2010，19（6）：79-81．

[3] 朱长江，郭艾，杨立洪，等．数学技术实验教学体系的构建与实验内容的设计[J]．数学教育学报，2016，25（1）：28-30．

[4] 高洁，周玮．在高等数学课程中开展数学实验教学的探索与研究[J]．数学教育学报，2015，24（3）：86-90．

[5] 喻平，董林伟，魏玉华．数学实验教学：静态数学观与动态数学观的融通[J]．数学教育学报，2015，24（1）：26-28．

[6] 吴绍兵，于明．关于课堂教学图形计算器使用恰当性的研究[J]．数学教育学报，2009，18（2）：59-62．

[7] 刘军彪．充分利用hp39gs优势提高教学有效性[J]．数学教育学报，2009，18（2）：66-68．

[8] 董林伟，孙朝仁．初中数学实验的理论研究与实践探索[J]．数学教育学报，2014，23（1）：20-25．

[9] 董林伟，郭瑞娟．丰富感知建立表象发展想像——例谈数学实验的教学功能[J]．中学数学教学参考（中旬），2015，（4）：63-65．

[10] 张志勇．迈开步，往前走：当下开展数学实验的实施建议[J]．教育与装备研究，2017，（1）：45-48．

Design Principle and Development Approach of Mathematical Micro Experiment in Middle School——Based on HP Prime Platform

ZHANG Zhi-yong

(No. 5 Middle School of Changzhou City, Jiangsu Changzhou 213001, China)

The change from teaching in the perspective of intelligence to the conscious cultivation of core literacy was inseparable from the soil of mathematics experiment. The mathematical micro experiment (similar to episodic experiment)put more emphasis on the short (experimental time), flat (simple operation) and fast (fast feedback) process, adopting mobile visual technology as a tool, supporting experiment and sharing at all times and places and often focused on mathematical knowledge (key and difficult point) or teaching procedure. It provided learners with fragmentation and mobilized experience, and could be easily embedded to the original teaching process meanwhile. As a mathematical verification, understanding or exploratory activity characterized by actual operation, the mathematical micro experiment supports the experiment and sharing anytime and anywhere. With the help of Hp prime platform, we could design and develop three categories and six kinds of micro experiments, such as scenario creation, phenomenon excavation, principle inquiry, method discovery, explanation construction, expansion and promotion, under the principles of operability, processability, re-creation and extensibility.

mathematical micro experiment; graphics calculator; mobile laboratory; core literacy

[责任编校：周学智]

G630

A

1004–9894（2017）04–0025–05

2017–02–09

江苏省教育科学“十二五”规划2015年度重点课题——高中数学可视化教学的实践研究（B-a/2015/02/010）；全国教育信息技术研究“十二五”规划2015年度课题——基于手持技术的高中数学可视化教学的实践研究（152732803）

张志勇（1974—），男，江苏江都人，中学高级教师，教育硕士，主要从事中学数学教育教学及信息技术与数学学科的整合研究．