考虑非遍历的抢修任务多目标动态调度

陈春良, 陈伟龙, 陈康柱, 刘彦, 史宪铭

(1.装甲兵工程学院 技术保障工程系, 北京 100072； 2.装甲兵工程学院 训练部, 北京 100072；3.军械工程学院 装备指挥与管理系, 河北 石家庄 050003)

考虑非遍历的抢修任务多目标动态调度

陈春良1, 陈伟龙1, 陈康柱2, 刘彦1, 史宪铭3

(1.装甲兵工程学院 技术保障工程系, 北京 100072； 2.装甲兵工程学院 训练部, 北京 100072；3.军械工程学院 装备指挥与管理系, 河北 石家庄 050003)

针对进攻作战中战损装备众多而抢修时间与抢修力量有限的矛盾，进行了进攻作战抢修任务动态调度研究。提出考虑非遍历的抢修任务多目标动态调度的现实军事问题，建立多目标规划数学模型，分析了非遍历、修理能力差异、待修装备优先级3个重要影响因素；根据所建模型的特点，设计了基于遗传算法的模型求解算法；运用Matlab软件进行了39辆待修装备、3个抢修组的动态调度示例仿真与分析。示例结果表明：通过实施机动伴随抢修和抢修任务动态调度，进攻作战部队能够获得约185 h的二次作战总时间，进而增强部队的持续作战能力，并大大减少决策工作量和决策时间、降低人为决策风险。

兵器科学与技术； 战场抢修； 动态调度； 非遍历； 遗传算法

0 引言

所谓遍历，是指沿着某条搜索路径，依次对集合中的每个元素均做一次且仅做一次访问。所谓非遍历，是指沿着某条搜索路径，依次对集合中的部分元素做一次且仅做一次访问，且由于受到边界条件限制，被访问元素数量具有不确定性。

所谓考虑非遍历的抢修任务多目标动态调度 (MDBTSPN)，是指在进攻作战中，敌方火力打击造成我方战损装备不断增多，而所属抢修力量有限，导致抢修力量无法在进攻周期内完成对修理范围内的所有待修装备的战场抢修；为最大限度地迅速恢复作战部队的整体进攻能力，在抢修任务调度过程中，需要综合权衡待修装备所需修理工时、转场所需时间、不同抢修组修理能力差异、待修装备优先级等因素，并考虑非遍历特性带来的根本性影响，从修理范围内的待修装备中选择部分装备进行修理。解决该问题的关键在于如何合理地建立多目标动态规划模型，动态地决策不同抢修组间的任务分工和同一抢修组内的抢修序列，使得抢修效果更有利于完成本阶段进攻作战任务。MDBTSPN作为一个典型复杂优化问题，是贴合战场实际情况且急需解决的一个军事难题，核心难点在于遵循MDBTSPN的实际约束限制，有效解决非遍历型寻优难题，动态追踪问题的最优解。

在战场抢修任务调度方面，由于战场环境复杂、限制条件多、研究难度大，现有战场抢修任务调度研究成果相对匮乏。文献[1-2]以战时定点维修为研究对象，提出了两种不同约束条件下的动态维修任务调度方法。文献[3]针对维修资源短缺及资源冲突的问题，建立了战场抢修多需求点多资源优化调度模型。文献[4]将证据推理应用于战时多任务抢修重要度决策，构建了重要度决策指标体系和决策模型。文献[5]以总抢修效益最大为目标，建立了抢修资源重组决策模型，设计了混合粒子群算法进行求解。已有研究或仅限定于战时定点维修，进而将问题转化为生产调度问题求解，或不考虑修理能力差异和修理力量损失，且均没有考虑非遍历这一约束，这既与MDBTSPN实际情况明显不符，也不能满足进攻作战对伴随保障的现实需求。

在动态调度及非遍历方面，研究热点主要集中于动态车辆路径问题[6]、生产调度问题[7-8]和多无人机协同任务分配问题[9]及三者的变体问题，焦点约束条件包括动态的需求集合[10]、时间窗[11]、多种类型的任务主体[12]、时间的不确定性[13]、费用[14]、动态环境[15]等。前述研究的数学实质绝大部分属于遍历型，少有对非遍历情况的考虑，且考虑到MDBTSPN的自身约束条件、目标函数、数学模型的特殊性，已有的模型、算法等均无法求解MDBTSPN.

从已掌握的文献分析，本文提出的考虑非遍历抢修任务动态调度问题作为一个复杂系统问题，尚无学者进行深入研究。据此，本文提出考虑非遍历的抢修任务动态调度这一军事问题，构建其数学模型，设计遗传算法并编程求解，通过示例仿真与分析验证算法有效性，解决非遍历型寻优难题并追踪MDBTSPN最优解的动态变化。MDBTSPN的高效解决能够为装备保障指挥员提供辅助决策支持，缩短保障决策时间，降低主观决策风险，提高进攻作战持续时间内的装备参战率。

1 模型建立

1.1 条件假设

1)开始抢修的时刻为0 min，进攻战斗结束时刻为Te；进攻战斗中，在时刻ti(i=0,1,…,N)产生新的待修装备，编号为i，其位置坐标(xi,yi),节点重要度为ρi，计划修理工时为Tri(人·h)，计划修理时间为Tsi(min)。

2)待修装备集合为J，始发点集合为I，抢修组集合为K，且|J|≥1，|I|≥1，|K|=m≥1，m为抢修组数量；无向图G=(V,E)，其中V=I∪J，E={(i,j)|i∈V,j∈J}. 各抢修组从不同初始位置出发，负责抢修其修理范围内的损伤装备(包括大部分轻损装备及少量维修工作量小的中损装备)，最终无需回到各自始发点。后文中提到的所有待修装备均是指抢修组修理范围内的损伤装备。

(1)

式中：i∈V,j∈J,i≠j.

(2)

式中：i∈J.

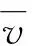
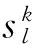
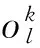
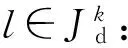
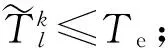
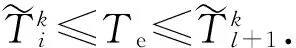
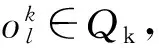
1.2 动态调度的处理方法设计

本文处理动态调度问题的总体思路是：由于在任意时刻t，MDBTSPN中的动态和静态需求信息均己知，引入滚动时域思想，基于本文设计的重调度驱动策略，将进攻周期内的动态调度问题P(t)转化为一系列离散时间点的静态调度问题P(ti)进行求解。

具体来说，就是根据在一体化进攻作战中抢修任务调度的实际情况，合理设计重调度驱动策略，并根据不断出现的抢修需求信息，确定出各个重调度时刻t(q)(q=1,2,…)；由于时刻t(q)的动态和静态抢修需求信息均为己知，进而将进攻周期内的抢修任务动态调度问题P(t)离散化，转化成为基于各个重调度时刻的静态任务分配问题P(t(q))；在滚动的每一步，针对当前离散点的局部问题P(t(q))，在分析其约束条件和确定其目标参数的基础上，建立抢修任务多目标静态调度数学模型，并依据模型特点设计解析算法或智能优化算法求解各抢修单元的任务分配决策方案，确定不同抢修单元的任务分工及同一抢修单元的抢修序列；方案执行，进入下一个重调度周期。

考虑进攻作战中抢修任务动态调度的时效性和可操作性的要求，本文采用数量分批驱动策略。

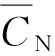
t(q)为重调度时刻，其确定公式为

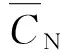
(3)

为将动态调度问题P(t)离散转化为静态任务分配问题P(t(q))，还需要判断和标定各个重调度时刻的抢修需求信息。为达成这一目的，须对抢修需要进行合理分类。

在任意时刻t，根据抢修组所在位置和任务完成情况，将所有抢修需求分为4类：1)已完成抢修的装备G1；2)抢修组正在抢修的以及正在前往抢修点路上的待修装备G2(已不可更改，称之为关键点)；3)已规划到抢修任务序列，但暂时没有抢修组前往的待修装备G3；4)新出现的待修装备G4. 其中ti时刻的关键点识别是解决动态调度问题的重要难点之一。

1.3 数学模型建立

进攻战斗战场抢修，旨在尽快恢复或部分恢复受损装备的任务功能，使其能够再次投入战斗，且修竣装备对作战装备体系的贡献率最大。

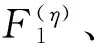
MDBTSPN的目标函数确定如下：

(4)

(5)

(6)

(7)

其中，(4)式表示：在有限的进攻作战持续时间内，各抢修组应尽可能多地修竣故障装备、优先修理节点重要度高的装备，并使其能够获得尽可能多的二次参战时间。

进一步将目标函数转化为

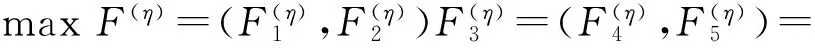
(8)

转化的原因在于：对于两种不同的抢修任务分配方案，如果在相同时间范围内，两种方案均能修竣1台营指挥车和1台战斗装备，且能赢得相同的二次作战时间总和，那么当目标函数采用(5)式时，则两种方案的目标函数值相同，即两种方案优劣程度相同；事实上，两种方案的优劣程度是不同的，因为营指挥车的节点重要度高于其他战斗装备，优先修竣营指挥车，其能更长时间地发挥指控功能，对于整个作战装备体系的贡献显然更大。基于此，本文采用(8)式所示的目标函数表达式。(8)式的实际意义可解释为：所有修竣装备的功能属性值与其发挥作用的时间长度乘积的代数和。

约束条件考虑了各抢修组修竣各个待修装备的时间约束关系、遍历与非遍历、各个待修装备是否被修竣、任一修竣的待修装备有且仅由一个抢修组完成。约束条件的具体数学关系式为

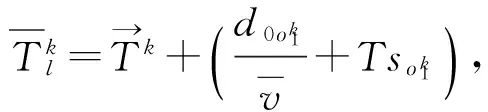
(9)

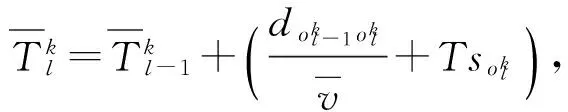
(10)

(11)

(12)

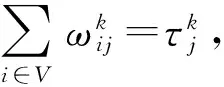
(13)

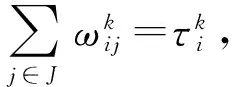
(14)

式中：(9)式表示抢修组k从各自任务起点出发到完成第1个待修装备抢修的计划修竣时刻之间的时间约束关系；(10)式表示ok中，由抢修组k完成抢修的相邻两车的计划修竣时刻之间的时间约束关系；(11)式表示任一抢修组只在进攻战斗结束前进行抢修，用以保证非遍历的实现；(12)式表示如果i点任务完成，则有且仅有某一个抢修组严格访问一次；(13)式表示任意一条弧的终点待修装备仅有一个起点待修装备与之相连；(14)式表示任意一条弧的起点待修装备仅有一个终点待修装备与之相连。

2 模型分析

2.1 非遍历分析

时间限制是导致非遍历问题出现的根本原因，非遍历型问题的实质是从num_veh中取n(n具有不确定性)、规模为n的遍历型问题。MDBTSPN内含了遍历与非遍历两种抢修任务调度问题，其模型及算法需要同时考虑这两种情况，求解难度显著增大，算法难以收敛。

2.2 修理能力差异分析

由于敌火威胁将直接导致修理力量的损失，进而造成各抢修组的修理能力产生差异。这种差异包括各抢修组之间的修理能力差异和抢修组内部的修理工修理技能差异。

对于前者，在每次任务调度开始前统计抢修力量损失，纳入模型进行计算。针对关键点待修装备，若抢修组正在前往该抢修点的路上，理应采用重调度后的修理力量进行计算；若抢修组正在抢修该装备，采用重调度前后各组修理力量的平均值进行计算。

对于后者，考虑修理工的修理水平差异，将其区分为初级修理工和高级修理工，设定前者每人每小时提供θ1，后者提供θ2，则任一待修装备计划修理时间为

(15)

2.3 待修装备优先级分析

在进攻作战过程中，进入抢修力量修理范围的待修装备主要包括指挥装备和主战装备。本文主要从待修装备的功能属性差异(指挥或主战)和任务属性差异(主攻与助攻)来分析其优先级。显然，同一级别的指挥装备与主战装备、不同级别的指挥装备、担任不同作战任务的主战装备，在进攻作战持续时间内发挥着截然不同的作用，也就具有了不同的待修装备优先级。

本文采用节点重要度作为待修装备优先级的评价参数，基于战场抢修原则“优先抢修指挥装备，尔后抢修主战装备”，通过定性分析，得到待修装备的节点重要度排序如下，从高到低分别是：高级别指挥装备，主攻方向的低级别指挥装备，助攻方向的低级别指挥装备，主攻方向的主战装备，助攻方向的主战装备。本文分别将上述5种装备的节点重要度分成5个等级：A、B、C、D、E.

3 模型求解方法设计

由于MDBTSPN是NP问题，针对其待修装备规模大、需要不断进行动态规划的特点，本文设计并编程实现遗传算法进行求解。

3.1 多目标处理方法确定

若采用经典的多目标决策方法处理MDBTSPN，如加权和方法、ε-约束法、目标规划法、极小极大法等，可通过不同方法将多目标优化问题转化为单目标优化问题进行求解。虽简单高效，但存在：1)参数的选取依赖于MDBTSPN的先验知识，不同的参数设置会产生不同的Pareto最优解；2)在大多数情况下，只能得到一个Pareto最优解，且该解的获取与参数设定存在很大关系。

带精英策略的非支配排序遗传算法(NSGA-II)[16]是非支配排序遗传算法 (NSGA)的改进算法，具有以下优点：1)提出的快速NSGA降低了计算的复杂度；2)采用拥挤距离比较算子代替了适值度共享方法，使得准Pareto域中的个体能均匀地扩展到整个Pareto域，保证了种群的多样性；3)引入了精英保留机制，有利于保存种群中的优良个体，提高种群的整体进化水平。

基于此，本文采用NSGA-II对MDBTSPN中的多目标问题进行处理，其核心是快速NSGA和拥挤距离比较算子的实现，目标是得到多个满意解或可接受的非劣解(即Pareto最优解)。在第η次调度中，首先求出MDBTSPN的Pareto最优解集，尔后装备保障指挥员根据该时刻的战场态势和决策策略，从Pareto最优解集选择出最满意解。

3.2 编码与解码设计

本文通过编码与解码来解决抢修任务动态调度中的非遍历约束，其解决思路为：1)通过设计两段式编码方式实现遍历情况下的抢修任务分配；2)通过非遍历约束及解码，计算得到截点位置信息，依靠截点位置来确保非遍历约束的实现。

在两段式编码中，前段采用顺序编码，用以确定抢修组间的任务分工；后段采用整数编码，用以表示断点位置。该编码方式简单直观，不仅满足了约束条件中的(10)式和(11)式，且染色体与解一一对应，遗传操作不会产生不可行解。

编码示例如图1所示，设定某染色体X=(3,10,2,6,8,1,7,4,5,9,3,7),|J|=10,m=3，断点为(3,7)，用竖虚线表示。

图1 编码示例Fig.1 Encoding example

解码时，根据约束条件中的(9)式～(12)式及其他约束，编程计算出截点位置和适应值，进而可求得3个抢修组的任务分工、各组抢修序列、该染色体的适应值。

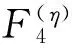
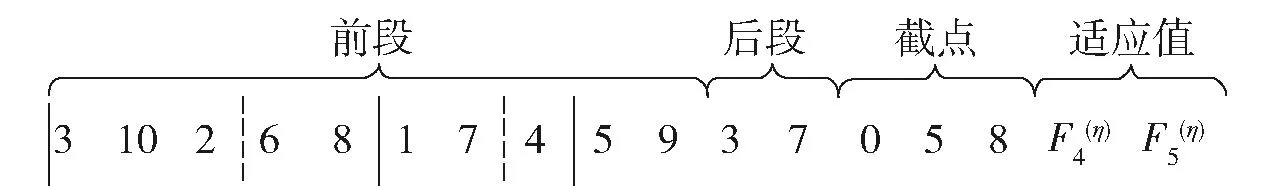
图2 解码示例Fig.2 Decoding example

3.3 遗传算子设计

染色体由2段编码组成，各段编码方式与现实意义各不相同，无法直接采用模拟二元交叉等方式进行交叉变异。为增大搜索范围、方便快速收敛，本文设计了融合式遗传操作算子，即采用二元锦标赛选择从上一代染色体中选出1/4的个体作为父代染色，对每一条父代染色体进行下列4种操作：

1)前段采用倒置操作，后段采用随机更新操作；

2)前段采用滑动平移操作，后段采用随机更新操作；

3)前段采用互换操作，后段采用随机更新操作；

4)前段不进行任何操作，后段采用随机更新操作。

将遗传操作产生的子代染色体与父代染色体按适应值大小进行整体降序排列，取前pop_size条作为新的染色体种群。

3.4 算法流程设计

基于遗传算法的抢修任务动态调度总体算法流程，如图3所示。

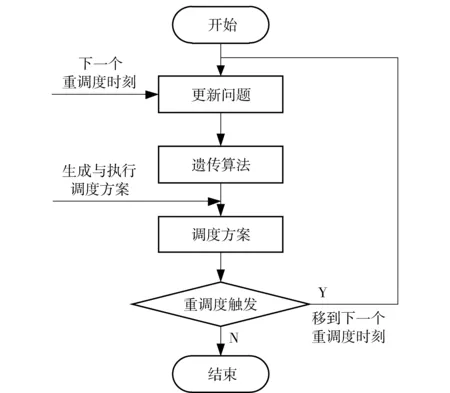
图3 总体算法流程Fig.3 Flow chart of overall algorithm

具体步骤如下：

1)初始化相关参数。

2)生成初始规划路径种群{S}。

4)采用NSGA-II进行非支配排序和个体间拥挤距离计算。

5)令iter=1.

6)采用二元锦标赛选择从pop_chm中优选出数量规模为pool_size的parent_chm.

7)进行遗传操作，产生offspring_chm.

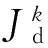
9)运用NSGA-II对集合{parent_chm,offspring_chm}进行快速非支配排序和个体间拥挤距离计算。

10)利用二元锦标赛选择和比较算子从{parent_chm,offspring_chm}中筛选出基因较优的新一代pop_chm.

11)判断iter≤num_iter？成立，转步骤12；否则，转步骤13.

12)iter=iter+1，转步骤5，进行新一轮寻优。

13)停止迭代，得到本次抢修任务调度的Pareto最优解集，依据该时刻的决策策略从Pareto最优解集中选出最满意解，转步骤14.

14)判断重调度驱动策略是否满足？是，转步骤15进行重调度；否则，转步骤25.

15)令k=1.

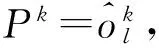
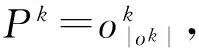
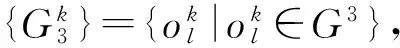
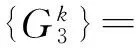
22)判断k<|K|?成立，转步骤23；否则，转步骤24.

23)k=k+1，转步骤16.

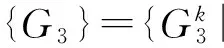
25)输出结果。

3.5 算法复杂度分析

对于抢修任务动态调度问题，设其种群规模为P，迭代次数为G，问题规模为N，目标数量为T. 本文设计的遗传算法，其算法复杂度可分析如下：

1)初始化算子的时间复杂度是O(PN2)；

2)解码算子的时间复杂度是O(N2)；

3)快速非支配排序算子的时间复杂度是O(TN2)；

4)选择算子的时间复杂度是O(P)；

5)遗传操作算子的时间复杂度是O(PN2)；

6)替换算子的时间复杂度是O(N)；

7)状态判断算子的时间复杂度是O(N2)。

根据遗传算法的框架，可计算其时间复杂度：

O=O(PN2)+O(TN2)+G(O(P)+O(PN2)+
O(TN2)+O(N))+O(N2)≈GPO(N2)。

分析决定该算法时间复杂度的核心因素，在于遗传操作算子。而本文为实现父代染色体的交叉变异而设计的4种遗传操作算子，其本身的时间复杂度为O(P)，并不会导致较高的时间复杂度。究其原因，是因为遗传操作算子内含着解码算子，且解码算子的时间复杂度是O(N2). 而导致解码算子时间复杂度较高的原因在于，本文为解决抢修任务动态调度问题的多个实际约束(包括不同抢修组的任务分工、同一抢修组的抢修序列、非遍历)，设计了两段式编码，且前段采用了实数编码。而实数编码在解码过程中需要耗费大量时间来计算染色体的截点位置信息，以及各个目标函数的适应值。

4 示例仿真与分析

4.1 示例仿真

某月某日，M国以其机步101团为核心，对我西北边境Q地区突然发动进攻，突袭失利后，转入机动防御。我数字化机步27师遵照上级命令担任主攻任务，务求15 h内歼驱该敌。27师部署100台步兵战车、30台主战坦克、30台装甲突击车；配署3个综合抢修组，采用全域伴随保障模式，负责抢修120 min内能完成的轻度损伤及极少部分中度损伤的作战装备。进攻作战持续时间内，战损装备不断出现，如何动态地确定不同抢修组间的任务分工以及同一抢修组内的修理顺序。

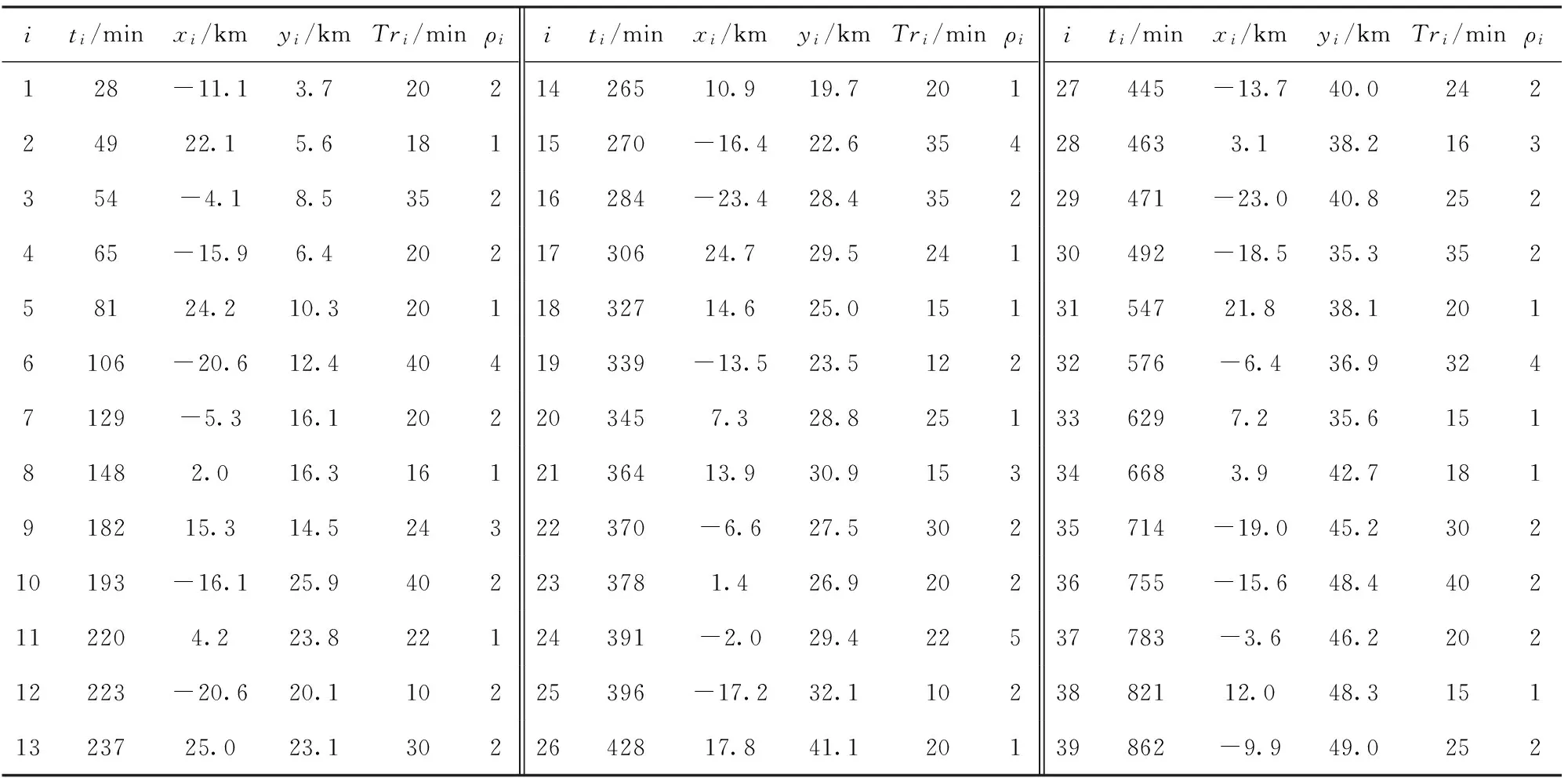
表1 待修装备信息

已知t=54 min时，战场已出现3辆损伤装备，此时抢修1组、2组、3组伴随进攻部队分别前进到(-2.8 km，-4.0 km)、(-15.7 km，-3.1 km)、(15.9 km，-5.6 km) 3点；装备保障指挥员下达指令，将其均分给3个抢修组。设定数量分批驱动策略阈值trg_num=5，尔后每次新的抢修需求达到阈值，即进行一次重调度，并运用算法求解。各抢修组的抢修力量变化信息如表2所示。

装备保障指挥员的既定决策策略为：对Pareto最优解集进行无量纲化处理，并采用加权法优选出最满意方案：

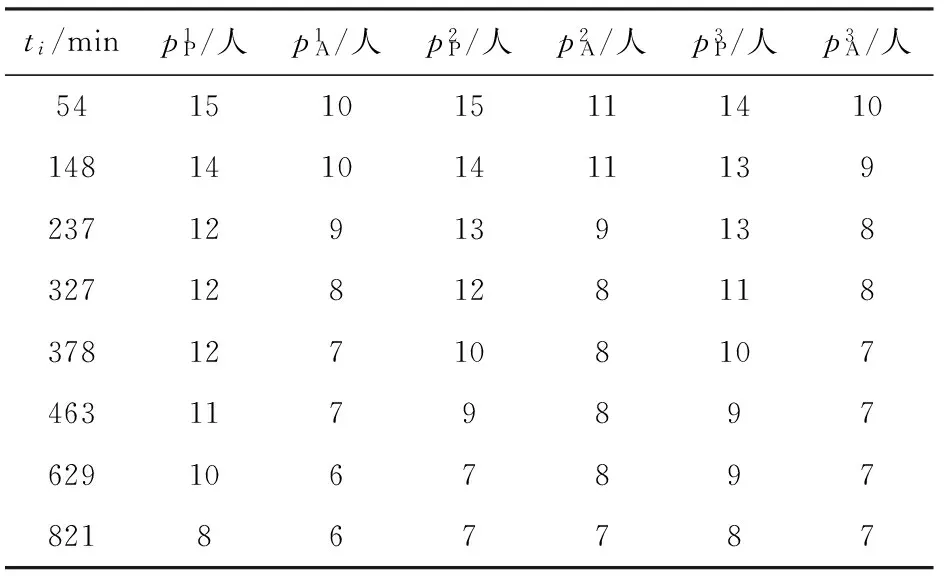
表2 抢修力量变化信息

(16)

式中：α、β为权重系数。

作战初期(当t<300 min)，需要较高的装备参战率以保证歼敌有生力量的顺利执行，α取较大值，α=0.7，β=0.3. 作战中后期(当t≥300 min)，为更有效地达成作战目的，作战装备间需要相互联合，β取较大值，α=0.4，β=0.6.

上述MDBTSPN案例，规划结果如表3所示。各抢修组的最终抢修序列如图4所示。

表3 规划结果

注：“无”表示该抢修组到重调度的开始时刻，已完成抢修序列中的所有任务，不存在关键点。

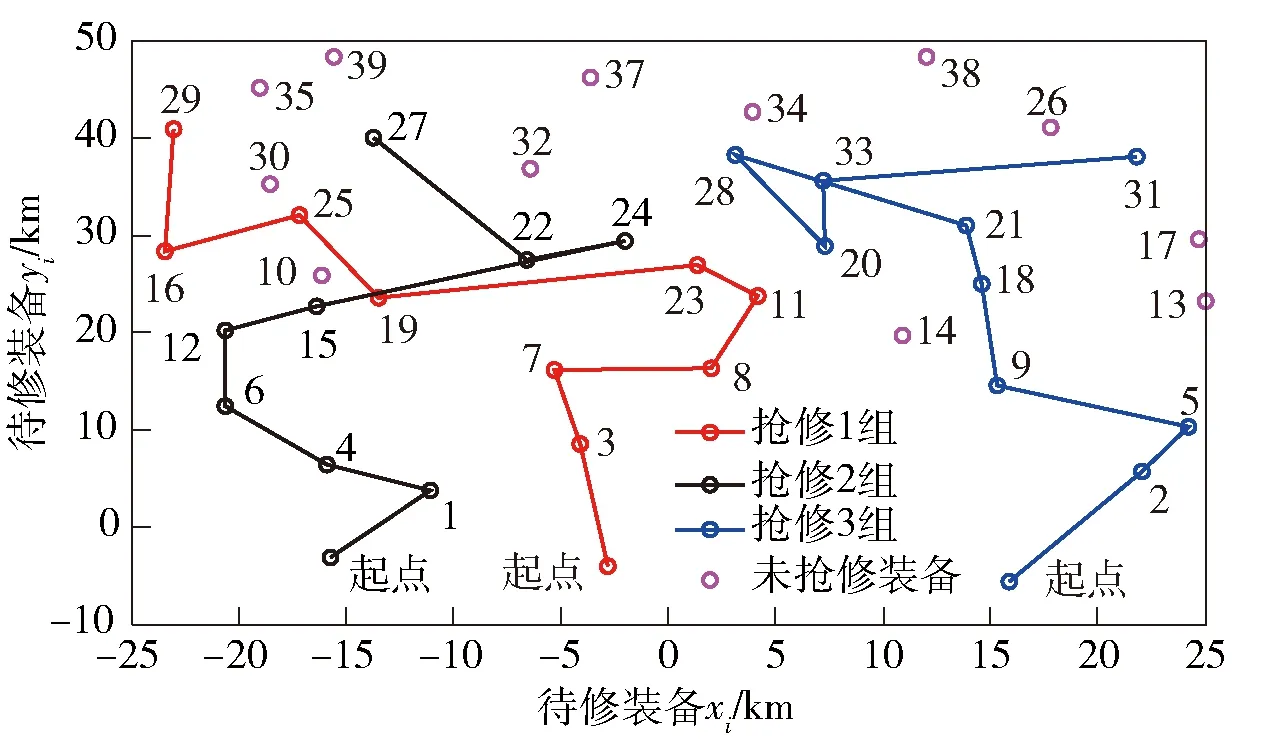
图4 最终抢修序列图Fig.4 Diagram of final rush-repair sequence

4.2 结果分析

1)由表3分析可知，到进攻战斗结束时，经抢修获得的二次作战总时间为11 103 min，约185 h；相当于为进攻部队增添了18辆可以参与10 h进攻作战的战斗装备，间接证明了实施伴随保障的重要性和建强伴随保障力量的必要性。

2)由表3分析可知，在时刻378 min，规划结果将待修装备22(故障时刻为370 min)安排在抢修1组的第7抢修顺位；但在时刻463 min进行重调度时，抢修1组还在抢修其他“关键点”装备19，待修装备22参与重调度，最后将其规划到抢修2组的第7顺位，并在时刻799 min才完成了抢修。类似的还有待修装备13、14、16、20、27. 虽然每一个抢修组的抢修序列对其自身而言不一定最优，但在各个规划时刻对整体而言是最优的。这样的动态调度为待修装备赢得了更多的修竣装备总量、节点重要度总和以及二次作战时间，直接证明了动态调度的优越性。

3)由表3分析可知，在时刻327 min和378 min，根据规划结果，待修装备17(故障时刻为193 min)分别被安排在抢修3组的第5顺位和第8顺位，但最终放弃了对其进行抢修。类似的“先被列入抢修计划，后又被放弃抢修”的待修装备还有10、14. 究其原因，在进攻作战初期，战损装备相对较少且抢修时间充裕，抢修组对所有待修装备进行遍历型抢修；随着累积的损伤装备越来越多，抢修组在规定时间内已无法完成对所有损伤装备的修理，只能进行非遍历型抢修；结果显示到进攻作战结束时刻，还有13辆损伤装备尚未进行抢修。这直接突显了非遍历型抢修与遍历型抢修的差异所在，且与战场抢修实际情况更加贴合。

4)深入分析表3和图4可知，在327 min，待修装备12和待修装备15同时参与重调度，抢修2组在完成关键点任务6后，放弃了节点重要度较高的待修装备15，优先修理了距离更近且维修工作量更小的待修装备12，体现了“优先抢修维修工作量小的战损装备”抢修原则。与此相反，在463 min，待修装备22和待修装备24同时参与重调度，抢修2组在完成关键点任务15后，放弃了距离更近的待修装备22，优先修理了装备优先级较高的待修装备24，体现了“优先抢修指挥装备，而后作战装备”的抢修原则。究其原因，为谋求整体抢修效果的最优(即获得尽可能多的修竣装备总量、节点重要度总和以及二次作战时间总和)，MDBTSPN综合权衡了多项抢修原则，通过算法在维修工作量大小、转场路程远近、待修装备优先级高低等多个相互制约的因素间进行了结果寻优。

5)由图4分析可知，在进行待修装备众多而Te有限的抢修任务动态调度时，将相继出现遍历型抢修与非遍历型抢修两种形态，最终各抢修组的任务分工呈现出相互交叉的全域保障趋势，旨在通过抢修组间的相互协作，在Te内从整体上谋得最佳的抢修效果，以维持进攻部队的持续进攻能力。

6)与此同时，由于待修装备众多，不同抢修组间的任务分工和同一抢修组内的抢修序列可能排列情况众多，以时刻463 min时的重调度为例，即有2.964 1×1012种可能的排列情况，人为找寻最优解难度大、耗时久；若战损装备数量较大，在有限时间内人为计算最优解几乎不可能。利用MDBTSPN模型及遗传算法编程求解，便于根据战场实际态势，调整模型参数及输入，动态、高效地求得问题的最优解。

5 结论

本文提出了MDBTSPN的现实军事问题，建立了其数学模型，设计并实现了基于遗传算法的模型求解，通过示例验证了模型能够有效解决非遍历型寻优难题、动态追踪问题的满意解。研究结论如下：

1)通过实施机动伴随抢修和抢修任务动态调度，能够获得约185 h的二次作战总时间，相当于增加了18辆可以参与10 h进攻作战的战斗装备，能够有力增强进攻部队的持续作战能力。

2)在进攻作战进程中，MDBTSPN模型及求解算法能够根据不断变化的抢修需求，不断调整抢修单元间的任务分工及抢修单元内的抢修序列，进而获得更高的抢修效益。

3)MDBTSPN模型及求解算法能够将“遍历”这一约束条件松弛为“非遍历”，扩大了模型的适用范围，且更加贴合作战实际。

4)MDBTSPN模型及求解算法能够大大减少保障指挥员的决策工作量和决策时间，降低人为决策风险，并提高抢修效益。

下一步主要研究方向：考虑不同重调度驱动策略对抢修任务动态调度结果的影响。

References)

[1] 王正元, 朱昱, 宋建社, 等. 动态维修任务调度的优化方法[J]. 机械工程学报, 2008, 44(1): 92-97. WANG Zheng-yuan, ZHU Yu, SONG Jian-she, et al. Optimal method on dynamic maintenance task scheduling [J]. Chinese Journal of Mechanical Engineering, 2008, 44(1): 92-97.(in Chinese)

[2] 王正元, 严小琴, 朱昱, 等. 一种考虑专业的动态维修任务调度的优化方法[J]. 兵工学报, 2009, 30(2): 252-256. WANG Zheng-yuan, YAN Xiao-qin, ZHU Yu, et al. An optimal method on dynamic maintenance task scheduling with subject taken into account[J]. Acta Armamentarii, 2009, 30(2): 252-256. (in Chinese)

[3] 曹继平, 宋建社, 朱昱, 等. 战场抢修多需求点多资源优化调度研究[J]. 兵工学报, 2008, 29(8): 995-1000. CAO Ji-ping, SONG Jian-she, ZHU Yu, et al. Research on battlefield maintenance optimization scheduling of multi-requirement-points and multi-resources[J]. Acta Armamentarii, 2008, 29(8): 995-1000. (in Chinese)

[4] 郭军, 宋建社, 杨檬, 等. 基于证据理论的多任务抢修重要度决策[J]. 系统工程与电子技术, 2011, 33(3): 581-584. GUO Jun, SONG Jian-she, YANG Meng, et al. Recovery importance decision making for multi-missions based on Dempster-Shafer theory[J]. Systems Engineering and Electronic, 2011, 33(3): 581-584. (in Chinese)

[5] 郭军, 宋建社, 曹继平, 等. 战场抢修资源重组决策方法[J]. 系统工程与电子技术, 2014, 36(2): 306-311. GUO Jun, SONG Jian-she, CAO Ji-ping, et al. Battlefield urgent maintenance resource recombination decision making[J]. Systems Engineering and Electronics, 2014, 36(2): 306-311. (in Chinese)

[6] Pillac V, Gendreau M, Guéret C, et al. A review of dynamic vehicle routing problems[J]. European Journal of Operational Research, 2013, 225(1): 1-11.

[7] Liu C H, Hsu C I. Dynamic job shop scheduling with fixed interval deliveries[J]. Production Engineering, 2015, 9(3): 377-391.

[8] Kuzmanovska A, Mak R H, Epema D. Dynamically scheduling a component-based framework in clusters[J]. Lecture Notes in Computer Science, 2015, 8828: 129-146.

[9] Moon S, Oh E, Shim D H. An integral framework of task assignment and path planning for multiple unmanned aerial vehicles in dynamic environments[J]. Journal of Intelligent and Robotic Systems, 2013, 70(1): 303-313.

[10] Sarasola B, Doerner K F, Schmid V, et al. Variable neighborhood search for the stochastic and dynamic vehicle routing problem[J]. Annals of Operations Research, 2016, 236(2): 425-461.

[11] Schneider M. The vehicle-routing problem with time windows and driver-specific times[J]. European Journal of Operational Research, 2016, 250(1): 101-119.

[12] Yepes V, Medina J. Economic heuristic optimization for heterogeneous fleet VRPHESTW[J]. Journal of Transportation Engineering, 2015, 132(4): 303-311.

[13] Lorini S, Potvin J Y, Zufferey N. Online vehicle routing and scheduling with dynamic travel times[J]. Computers & Operations Research, 2011, 38(7): 1086-1090.

[14] Letchforda A N, Nasiri S D. The Steiner travelling salesman problem with correlated costs[J]. European Journal of Operational Research, 2015, 245: 62-69.

[15] Akar E, Topcuoglu H R, Ermis M. Hyper-heuristics for online UAV path planning under imperfect information[J]. Lecture Notes in Computer Science ,2014, 8602:741-752.

[16] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.

Multi-objective and Dynamic Scheduling of Battlefield Rush-repair Tasks Based on Non-ergodicity

CHEN Chun-liang1, CHEN Wei-long1, CHEN Kang-zhu2, LIU Yan1, SHI Xian-ming3

(1.Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing 100072, China;2.Department of Training, Academy of Armored Force Engineering,Beijing 100072, China;3.Department of Equipment Command and Management, Ordinance Engineering College,Shijiazhuang 050003, Hebei, China)

In the offensive operation, equipment is constantly damaged, but the battlefield rush-repair time and power are limited. The dynamic scheduling of battlefield rush-repair tasks in the offensive operation is studied. A multi-objective and dynamic scheduling of battlefield rush-repair tasks based on non-ergodicity, which is a real military problem, is presented. A mathematical model of multi-objective programming is established. Three key factors, including non-ergodicity, repair ability difference and priority of equipment to be repaired, are analyzed. A scheduling example of 39 equipment to be repaired and 3 repair groups is simulated and analyzed by using Matlab. The simulated result shows that the proposed model is scientific and reasonable, and the algorithm is correct and efficient, which can effectively solve the difficult problem of non-ergodic optimization and dynamically track the change of the optimal solution.

ordnance science and technology; battlefield rush-repair; dynamic scheduling; non-ergodicity; genetic algorithm

2017-01-05

陈伟龙(1988—)，男，博士研究生。E-mail:amose_chen@163.com

陈春良(1963—)，男，教授，博士生导师。E-mail: chen1963@126.com

E92

A

1000-1093(2017)08-1593-10

10.3969/j.issn.1000-1093.2017.08.018