嵌入式共固化复合材料夹芯板结构的自由振动

翟彦春, 梁 森, 付小静

(1. 潍坊科技学院 机械工程学院， 山东 寿光 262700；2. 青岛理工大学 机械工程学院， 山东 青岛 266000)

嵌入式共固化复合材料夹芯板结构的自由振动

翟彦春1，2, 梁 森2, 付小静2

(1. 潍坊科技学院 机械工程学院， 山东 寿光 262700；2. 青岛理工大学 机械工程学院， 山东 青岛 266000)

基于一阶ZIG-ZAG理论和夹芯层的常复数模型，采用Navier解形式对铺层方式为(0°/90°/0°)的薄的四边简支三层夹芯板的自由振动进行分析。研究了在夹芯板总厚度不变的前提下，固有频率随着表层厚度的增加呈现先减小后增大的趋势，呈上凹抛物线状；损耗因子值随着表层厚度的增加呈现先增大后降低的趋势，分布呈下凸抛物线状，最大值出现在表层和底层厚度相等时，因此对称结构夹芯板为最优结构设计；在夹芯层厚度和位置一定的前提下，固有频率的值随着表层和底层厚度的增加而增大，损耗因子值随着表层和底层厚度的增加呈现先增加后减小的趋势，损耗因子存在最大值，为夹芯板结构的最优设计提供参考。

复合材料；夹芯板；自由振动；固有频率；损耗因子

嵌入式共固化复合材料(Embedded Co-cured Composite Damping Structure，ECCDS)不但保持了原有的材料动力学特性又提高了构件的阻尼性能，与传统材料相比具有良好的整体性能，如：热稳定性好、高比强、高比模、高阻尼及可裁剪性等等，因此在先进工业领域得到广泛应用[1-2]。在实际工程中，大量的复杂几何问题需要用板壳理论来解释，复合材料层合板和夹芯板是目前研究的热点方向。

文献[3]分析了复合材料层合板的拉伸疲劳特性，为疲劳损伤演化的分析提供了依据；Yang等[4]在一阶剪切变形理论基础上，提出一种适用于任何边界条件的傅里叶-里兹解(Fourier-Ritz Solution)，通过修正傅里叶级数与瑞利里兹法相结合，得到了较为精确的固有频率和损耗因子解。文献[5]基于一阶ZIG-ZAG理论和Kelvin黏弹性芯材本构特征模型，采用Navier解形式分析了四边简支的三层夹芯板的自由振动，探讨了阻尼层参数变化对结构固有自由振动特性的影响。文献[6]基于三阶等效单层板理论，采用有限元模型对层合板和夹芯板的弯曲和振动进行了研究。文献[7]基于Reddy分层理论分别对约束阻尼层合板的层间应力和自由振动进行了研究；文献[8]基于分层理论建立有限元模型，对层合板的自由振动和阻尼优化进行分析。文献[9]提出面向任意边界条件和任意非均匀载荷下的角铺设层合板的弯曲和应力分析的等效单层板理论。文献[10]对三层复合材料夹芯板的振动和阻尼进行分析，用虚位移原理得到了自由振动的关于截面力和力矩的本构方程，以及相关的边界条件，使用广义微分积分法求解上述特征方程，得到频率和损耗因子值。

目前四边简支三层夹芯板的自由振动研究中，重点在夹芯板平衡方程的理论模型推导、求解平衡方程和材料物理参数对自由振动的影响等等，鲜有相关文献探究薄的四边简支夹芯板的最优结构布置形式。由于目前复合材料夹芯板在实际工程中的大量应用，因而有必要探究薄夹芯板的最优结构设计。

为了探究薄夹芯板的最优结构设计，本文基于一阶ZIG-ZAG理论和夹芯层常复数模型，采用Navier解形式对铺层方式为(0°/90°/0°)的薄四边简支三层夹芯板的自由振动进行分析，得到的结论可为三层薄夹芯板的最优结构设计提供参考。研究了在夹层板总厚度不变的前提下，芯层不同位置对固有频率和损耗因子的影响，以及在夹芯层厚度和位置一定的前提下，研究了表层和底层不同厚度对固有频率和损耗因子的影响。

1 夹芯板控制方程的推导及求解

1.1 基本假设

为了推导铺层为(0°/90°/0°)的薄的四边简支三层夹芯板的控制方程及各运动关系，我们做出如下假设：层间界面无滑移；表层和底层板均为正交对称各向异性层合板，位移符合基尔霍夫假设；垂直于板面方向的变形忽略不计，即εz=0；黏弹层板为正交铺设层合板，只考虑剪切变形且剪切模量为常复数形式，泊松比为常数。

为了建立夹芯板的位移坐标系，规定各层板的Z向坐标以各层板的中面为基准。复合材料夹芯板的几何结构及尺寸，如图1所示；位移坐标及面内位移关系图，如图2所示。

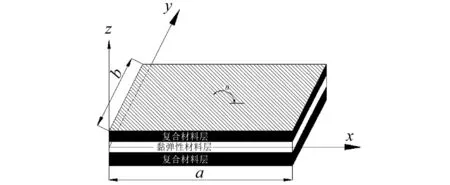
图1 夹芯板的几何结构及尺寸Fig.1 Geometry and configuration of the sandwich plate

图2 夹芯板的面内位移Fig.2 In-plane displacement of sandwich plate

1.2 位移-应变关系

根据所做出的假设和坐标系规定，表层和底层板的位移表达式为

(1)

根据层间界面无滑移的假设条件，夹芯层中面位移表达式为

(2)

式中：u2，v2分别为夹芯层中面位移；α2，β2分别为夹芯层法线相对于x、y轴的转角。

进而可以推导出夹芯层的位移表达式为

(3)

第i层的位移-应变关系表达式为

(4)

式中，i=1,2,3。

1.3 截面法向力、剪力、弯矩的表达式

阻尼层的剪力表达式为

(5)

则表层和底层板上的法向力和弯矩的表达式为

(6)

(7)

1.4 复合材料夹芯板控制方程的推导

(8)

1.5 复合材料夹芯板控制方程的求解

四边简支复合材料夹芯板的自由振动边界条件为

x=0,a:

项目施工实际安全保障水平是项目安全状态在考核期内的量化体现。安全保障水平越高，项目越安全，发生安全事故的可能性就越小。以施工安全保障水平指标评价体系为基础，对各项指标进行定量和定性分析，获得项目施工实际安全保障水平。

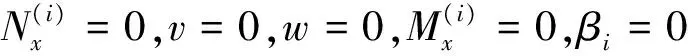
y=0,b:

i=1,3。

采用Navier型解法，满足四边简支边界条件的位移函数表达式为

u1(x,y,t)=U1cos(nπx/a)sin(mπy/b)eiω*t

v1(x,y,t)=V1sin(nπx/a)cos(mπy/b)eiω*t

w(x,y,t)=Wsin(nπx/a)sin(mπy/b)eiω*t

u3(x,y,t)=U3cos(nπx/a)sin(mπy/b)eiω*t

v3(x，y,t)=V3sin(nπx/a)cos(mπy/b)eiω*t

(9)

M[-(ω*)2]X=(K+jC)X

(10)

式中：M为质量矩阵;(K+jC)为刚度矩阵;X=(U1,U3,V1,V3,W)T。

板的圆频率和损耗因子按式(11)计算[11]

(11)

2 实例分析

2.1 数值计算

为了检验所推导的公式的正确性,分别计算文献[11]中的(0/90/0)铺设的四边简支夹芯板的振动频率和损耗因子，材料参数分别见表1和表2，并与文献值对照。

表1 材料参数

表2 材料参数

表3和表4列出了本文计算的频率和损耗因子与文献[11]中的数据的对比，可以看出固有频率的误差在7%以内，1～3阶损耗因子的误差在5%以内，4阶损耗因子误差9.8%。表4中的误差较大是因为式(8)基于经典层合板理论，忽略了剪切变形的影响，而表4中的数据是基于高阶剪切变形理论，考虑了剪切变形对频率和损耗因子的影响，从整体看计算结果说明所推导的公式是正确和可靠的。

表3 固有频率和损耗因子计算结果

表4 固有频率和损耗因子计算结果

2.2 表层和底层厚度和一定条件下，改变夹芯层中面位置

从图3中可以看出，不同模态下的损耗因子值随着夹芯层位置下移(表层厚度的增加)呈现先增大后减小的趋势，呈上凸抛物线状，最大值出现在表层和底层厚度相等时，即h1=h3，夹芯板为对称结构，之后逐渐降低，这是因为在对称结构下，夹芯层会产生最大的剪应力来消耗振动，因此在夹芯板的设计中对称结构为最佳设计，损耗因子值为最大值。从图4中可以看出，固有频率随着夹芯层位置下移(表层厚度的增加)呈现先减小后增大的趋势，呈上凹抛物线状，最小值出现在表层和底层厚度相等时，即h1=h3。综合说明对称结构夹芯板在几和尺寸不变的前提下具有最大损耗因子和最小固有频率，为最佳设计。

图3 损耗因子随夹芯层中面位置变化(h1+h3为定值)Fig.3 Variation of the loss factor with mid-plane of h2(constant h1+h3)

图4 固有频率随夹芯层中面位置变化(h1+h3为定值)Fig.4 Variation of the frequency with mid-plane of h2(constant h1+h3)

2.3 夹芯层厚度和位置一定的前提下，同时改变表层和底层厚度

从图5和图6中可以看出，在夹芯层厚度和位置一定的前提下，固有频率的值随着表层和底层厚度的增加而增大，1阶损耗因子的值随着表层和底层厚度的增加而增加，达到最大值后基本保持不变，但是2～4阶损耗因子的值随着表层和底层厚度的增加呈现非常明显的先增加后减小的趋势，1～4阶损耗因子都存在最大值。

图5 损耗因子随表层厚度h1的变化(h1=h3)Fig.5 Variation of the loss factor with h1(h1=h3)

图6 固有频率随表层厚度h1的变化(h1=h3)Fig.6 Variation of the frequency with h1(h1=h3)

3 结 论

本文基于一阶ZIG-ZAG理论和夹芯层的常复数模型，采用Navier解形式对铺层方式为(0°/90°/0°)的薄的四边简支三层夹芯板的自由振动进行分析。结果表明：

(1)在夹芯板厚度不变的前提下，固有频率随着表层厚度的增加呈现先减小后增大的趋势，呈上凹抛物线状，最小值出现在表层和底层厚度相等时；不同频率下的损耗因子的变化情况具有很高的一致性，损耗因子值随着表层厚度的增加呈现先增大后降低的趋势，分布呈抛物线状，最大值出现在表层和底层厚度相等时，因此对称结构夹芯板的损耗因子最大。

(2)在夹芯层厚度和位置都不变的前提下，固有频率的值随着表层和底层厚度的增加而增大，一阶损耗因子的值随着表层和底层厚度的增加而增加，达到最大值后基本保持不变，但是2～4阶损耗因子值随着表层和底层厚度的增加呈现非常明显的先增加后减小的趋势，1～4阶损耗因子都存在最大值。

[ 1 ] 梁森，梁磊，米鹏. 嵌入式共固化复合材料阻尼结构的新进展[J].应用力学学报, 2010, 27(4):767-771.

LIANG Sen, LIANG Lei,MI Peng. New development of the embedded and co-cured composite damping structres[J]. Chinese Journal of Applied Mechanics, 2010, 27(4):767-771.

[ 2 ] 许广举,陈庆樟,李学智,等.复合阻尼材料降低柴油机噪声的试验研究[J]. 机械设计与制造, 2015(5):160-163.

XU Guangju,CHEN Qingzhang,LI Xuezhi, et al. Experimental study on reducing noise of diesel engine by composite damping material[J].Mechinery Design & Manufacture, 2015(5):160-163.

[ 3 ] 李祚军, 张娟, 王佩艳,等. T700/3234碳纤维层合板的拉伸疲劳特性分析[J]. 机械设计与制造, 2013(10):4-6.

LI Zuojun，ZHANG Juan，WANG Peiyan, et al.Tensile and fatigue properities of T700/3234 carbon fiber reinforced composite laminates[J]. Mechinery Design & Manufacture, 2013(10):4-6.

[ 4 ] YANG C, JIN G, YE X, et al. A modified Fourier-Ritz solution for vibration and damping analysis of sandwich plates with viscoelastic and functionally graded materials[J]. International Journal of Mechanical Sciences, 2016, 106:1-18.

[ 5 ] 杨坤, 梅志远,李华东.黏弹性芯材复合材料夹芯板的自由振动分析[J].海军工程大学学报, 2012, 24(5):6-11.

YANG Kun,MEI Zhiyuan, LI Huadong. Analysis of free vibration of composite sandwich with viscoelastic core layer[J]. Journal of Naval University of Engineering, 2012, 24(5): 6-11.

[ 6 ] TU T M, LE N T, QUOC T H. Finite element modeling for bending and vibration analysis of laminated and sandwich composite plates based on higher-order theory[J]. Computational Materials Science, 2010, 49(4):390-394.

[ 7 ] 胡明勇, 王安稳. 纤维增强黏弹性复合材料层合板的自由振动和应力分析[J]. 工程力学, 2010, 27(8):10-14.

HU Mingyong,WANG Anwen.Free vibration and stresses analysis of fiber-reinforced viscoelastic composite laminated plates[J]. Engineering Mechanics, 2010, 27(8):10-14.

[ 9 ] ALIPOUR M M. An analytical approach for bending and stress analysis of cross/angle-ply laminated composite plates under arbitrary non-uniform loads and elastic foundations[J]. Archives of Civil & Mechanical Engineering, 2016, 16(2):193-210.

[10] ARIKOGLU A, OZKOL I. Vibration analysis of composite sandwich plates by the generalized differential quadrature method[J]. Aiaa Journal, 2012, 50(3):620-630.

[11] CUPIAL P, NIZIOL J. Vibration and damping analysis of a three-layered composite plate with a viscoelastic mid-layer[J]. Journal of Sound & Vibration, 1995, 183(1):99-114.

Free vibration of a embedded co-cured composite sandwich plate

ZHAI Yanchun1,2, LIANG Sen2, FU Xiaojing2

(1. College of Mechanical Engineering, Weifang University of Science and Technology, Shouguang 262700,China;2. College of Mechanical Engineering, Qingdao Technological University, Qingdao 266000, China)

Analysis of free vibration of a thin composite sandwich plate with four simply supported edges and (0°/90°/0°) laying-up was conducted using the Navier solution based on the first-order ZIG-ZAG theory and a constant complex model. On the condition that the thickness of the total plate remained unchanged, nature frequency that tended to go from descent to ascent with the increase of the thickness of surface layer presented a concave parabolic distribution; loss factor that tended to go from increase to decrease with the ascent of the thickness of surface layer presented a concave parabolic distribution. So the symmetrical structure sandwich plate is the optimal structure design. On the condition that thickness and location of viscoelastic layer remains as constants, the natural frequencies can be improved with the increase of thickness of the surface layer; loss factor tended to go from increase to decrease with the ascent of the thickness of the surface layer and presented a parabolic distribution. All of this can provide the reference for the optimal design of sandwich plate structure.

embedded co-cured composite; sandwich plate; free vibration; natural frequency; loss factor

国家自然科学基金(51375248)

2016-05-13 修改稿收到日期： 2016-09-21

翟彦春 男，博士生，1984年11月生

梁森 男，博士，教授，1962年6月生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.16.036