环境温变对纤维增强夹芯板临界热屈曲温度的影响

杨 洁，薛 宇，李金强，2，武晓刚，高海峰，2，冯 伟

(1.太原理工大学 机械与运载工程学院，太原 030024；2.超达阀门集团股份有限公司，浙江 温州 325000； 3.中车齐齐哈尔车辆有限公司，黑龙江 齐齐哈尔 161000)

纤维增强复合材料比普通材料具有许多突出的优点，如强度高、耐高温、重量轻等。近年来，正在逐步取代钢板用于民用和航空领域，尤其是由高性能纤维和高性能基体组成的复合材料，其力学性能十分突出[1]。国内外已有大量学者对纤维增强复合材料结构的热屈曲进行了研究。

徐新生等[2]利用辛方法研究了由于温度引起的弹性圆板的热屈曲问题，该方法可以给出一个完备的本征解空间，或圆板热屈曲问题的模态空间。袁武等[3]对均匀温度场下金属点阵夹芯板的临界热屈曲温度进行了求解和参数影响分析，研究表明，四边固支条件下夹层板的临界屈曲温度要远高于四边简支条件下的临界屈曲温度。田新鹏等[4]研究了水平方向非均匀温度场下层合板的热屈曲行为，指出在非均匀温度场下层合板的临界屈曲温度受温度分布、振动模式、边界条件的影响。卿光辉等[5]基于三维状态空间理论体系，导出的层合板三维状态方程可为分析其他边界条件问题提供参考。KANT et al[6]使用有限元方法对热载荷作用下倾斜纤维增强复合材料层合板和夹芯板屈曲进行了研究。结果表明，临界热屈曲温度随着倾斜角度的增大而增大，薄板中增加的幅度大于厚板。HAN et al[7]研究了泡沫填充复合波纹夹芯板在热载荷作用下的自由振动和屈曲行为。该研究为泡沫填充复合材料夹层板在机械和热载荷作用下的振动和稳定性分析提供了一种有效的方法，可推广到其他类型的夹层板或多层夹层板。LI et al[8]用四变量理论给出了梯度材料夹层板的机械和热屈曲的解析解。JIN et al[9]使用ABAQUS软件分别研究了复合材料圆板和钛合金圆板在不同边界条件下的热屈曲问题。结果表明，DIC技术能够得到复杂结构的全局变形和热屈曲。

目前针对夹芯板热屈曲性能方面的研究工作中，已有学者对夹芯板在均匀温度分布和水平方向非均匀温度分布下的热屈曲性能进行了研究；但对于在厚度方向非均匀温度分布下夹芯板热屈曲性能方面的工作还鲜有报道。因此，本文基于三角剪切变形理论，利用哈密顿原理推导出了夹芯板的控制方程。该理论是基于位移的等效单层理论，利用平面内位移厚度坐标的三角函数计算平面外剪切应变。运用假设模态法求解了夹芯板在不同温度分布下的临界热屈曲温度，并讨论了边界条件、长厚比、长宽比、hf/h和铺层纤维角度对夹芯板临界热屈曲温度的影响。

1 基本理论

对称复合材料夹芯板的长、宽、厚分别为a，b，h，面板厚度为hp，芯层厚度为hc.如图1所示。取夹芯板中面为x-y坐标平面，z轴垂直于x-y坐标平面。坐标原点位于夹芯板中面中心。

在板上任意点(x，y，z)的位移可写为[14]：

(1)

式中：u0，v0分别是在x和y方向上中面的位移。wb和ws分别为弯曲和剪切分量的挠度。

将方程(1)代入应变-位移关系中可得板中应变分量为：

(2)

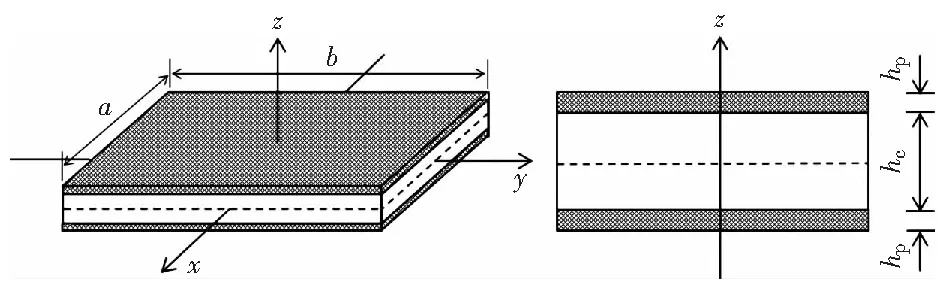
图1 复合材料夹芯板的几何结构Fig.1 Geometry of composite sandwich plate

第k层应力-应变关系为：

(3)

第k层热膨胀系数为：

(4)

层合板的总应变能U和总动能T可表示为：

(5)

(6)

其展开式见附录A.

为了满足夹芯板任意边界条件，引入位移向量u0，v0，w0.其详细表达式可见第二部分计算方法。在装配了位移分量形式之后，系统的运动方程可以用哈密顿原理推导出来，其表达式如下：

(7)

式中：M，KL，KT分别时整个系统的广义质量矩阵、刚度矩阵和温度刚度矩阵。其表达式见附录B.

热屈曲是当载荷达到某一临界值时，结构构形突跳到另一个随遇的平衡状态的现象。为了计算夹芯板的临界热屈曲温度，略去哈密顿原理中的与时间导数有关的项(动能项)[15]，可以得到矩阵形式的夹芯板热屈曲问题的控制方程为：

(KL-λKT)X=0 .

(8)

对于给定的温度分布函数FΔT，可以通过求解式(8)来获得临界热屈曲温度ΔTcr.

2 计算方法

本文采用假设模态法求解了夹芯板的临界热屈曲温度。假设模态法是连续系统的一种离散化方法，它是利用有限个已知的模态函数线性组合近似确定系统的响应。应用假设模态法，将位移表示成模态函数乘以广义坐标的形式[10-11]：

(9)

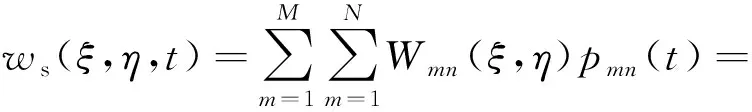
(10)

(11)

(12)

式中：p(t)=[p11(t),…,pMN(t)]T，r(t)=[r11(t),…,rIJ(t)]T，s(t)=[s11(t),…,sKL(t)]T为系统的广义坐标；W(ξ,η)=[W11(ξ,η),…,WMN(ξ,η)]T，U(ξ,η)=[U11(ξ,η),…,UIJ(ξ,η)]T，V(ξ,η)=[V11(ξ,η),…,VKL(ξ,η)]T为满足系统几何边界条件的模态函数。

将上述模态函数代入式(7)和式(8)中的广义质量矩阵M、刚度矩阵KL和温度刚度矩阵KT.利用MATLAB进行编程求解，得到夹芯板的临界热屈曲温度。

3 结果和讨论

本文通过MATLAB软件对夹芯板进行数值模拟。为了验证本文公式和模型的有效性，用本文方法计算了夹芯板的临界热屈曲温度，并与已有计算结果进行了对比。

表1 夹芯板的材料属性Table 1 Material properties of sandwich plates

图2比较了本文计算方法得到的复合材料夹芯板的临界热屈曲温度与已有文献的数值结果。从图中可以看出本方法计算的结果与其他研究人员的数值结果有良好的一致性。存在误差的原因有以下几点：1) 文献[12]中的理论只有3个未知变量，而本文采用的理论有4个未知变量而且该理论利用平面内位移厚度坐标的三角函数计算平面外剪切应变；2) 文献[7]与本文理论中采用的形状函数不同。

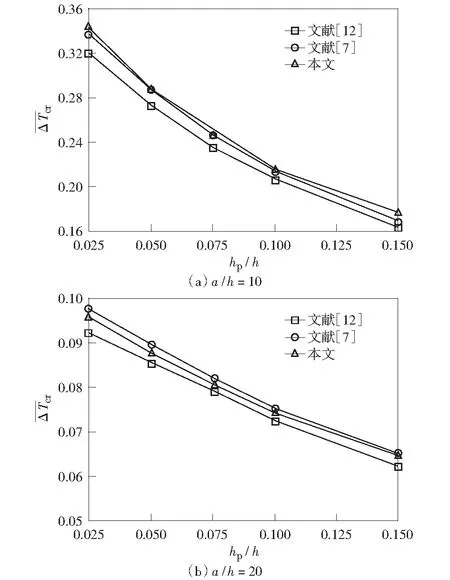
图2 本文分析方法的计算结果与文献[7]与[12]分析结果的比较Fig.2 Comparison of the results deduced from present analysis with the prediction of [7] and [12]

假设温度仅沿夹层板厚度方向变化。温度分布函数为[13]：

式中：β是温度敏感指数。

夹芯板的铺设方式为图3所示，长厚比为a/h=20，面板厚度与总厚度的比值hp/h=0.10.

图3 复合材料夹芯板的铺层方式[0°/90°]5[Core][90°/0°]5Fig.3 Stacking sequence [0°/90°]5[Core][90°/0°]5 of composite sandwich plates

图4给出了不同边界条件下临界热屈曲温度随指数的变化情况。由图中可知随着温度函数指数γ的增大夹芯板临界热屈曲温度逐渐增大。四边固支边界(CCCC)夹芯板的临界屈曲温度最大是由于固支边界的约束最强。随着夹芯板的宽度减小，对边简支对边固支边界(SCSC)夹芯板的临界热屈曲温度与四边固支边界夹芯板的临界热屈曲温度的差距逐渐减小，与四边简支边界(SSSS)夹芯板的临界热屈曲温度的差距逐渐增大。该结果的产生是由于夹芯板的宽度对应对边简支对边固支边界的简支边界，随着宽度的减小，固支边界的影响大于简支边界的影响。对边固支对边自由边界(CFCF)夹芯板的临界热屈曲温度的变化情况与对边简支对边固支边界夹芯板的临界热屈曲温度类似。随着夹芯板宽度的减小刚度逐渐增大，夹芯板的临界热屈曲温度逐渐增大。

图4 不同边界条件下临界热屈曲温度随指数的变化情况Fig.4 Critical thermal buckling temperature difference vs. index β under different edge conditions

现研究长厚比对临界热屈曲温度的影响。

图5给出了不同长厚比下，复合材料夹芯板临界热屈曲温度随长厚比的变化情况。从图5中可以看出，不同温度分布下相同边界条件复合材料夹芯板临界热屈曲温度变化趋势相同，而且临界热屈曲温度随着长厚比的增大而减小。随着厚度的减小，夹芯板的刚度在逐渐减小，临界热屈曲温度减小。相同边界条件下，由于均匀温度分布夹芯板的温度刚度矩阵最大，非线性温度分布夹芯板的温度刚度矩阵最小，所以均匀温度分布夹芯板的临界热屈曲温度最小，非线性温度分布夹芯板的临界热屈曲温度最大。四边固支边界夹芯板的临界屈曲温度最大。这是由于固支边界的约束要强于简支边界和自由边界。

图5 临界热屈曲温度随长厚比的变化情况Fig.5 Critical thermal buckling temperature difference vs. side-to-thickness ratio a/h

现研究hp/h对临界热屈曲温度的影响。复合材料夹芯板的长厚比为a/h=20，铺设方式如图3所示，边界条件为四边简支，长方形夹芯板长宽比为a=2b.

从图6中可以看出，随着hp/h的增大夹芯板临界热屈曲温度逐渐减小。均匀温度夹芯板临界热屈曲温度最小，非线性夹芯板临界热屈曲温度最大。由于长方形夹芯板的宽小于正方形夹芯板的宽，导致夹芯板刚度增大。因此，在四边简支边界条件下长方形夹芯板的的临界热屈曲温度大于正方形夹芯板的临界热屈曲温度。与长方形夹芯板相比，非线性温度分布下正方形夹芯板的临界热屈曲温度随hp/h的变化较小。

图6 临界热屈曲温度随hp/h的变化情况Fig.6 Critical thermal buckling temperature difference vs. face-to-thickness ratio hp/h

现研究纤维角度对临界热屈曲温度的影响。边界条件为四边简支，长方形夹芯板长宽比为a=2b.

图7给出了长厚比a/h=20，铺设方式为[θ/Core/θ](0°<θ<180°)，hp/h=0.100，临界热屈曲温度随纤维角度的变化情况。从图7(a)中可以看出，正方形夹芯板临界热屈曲温度的最大值出现在纤维角度θ为45°和135°附近。从图7(b)中可以看出，对于长方形夹芯板，临界热屈曲温度的最大值出现在纤维角度θ为60°和120°附近。说明，夹芯板的长宽比对夹芯板临界屈曲温度最大值所对应的纤维角度有很大的影响。同样，均匀温度分布夹芯板的临界热屈曲温度最小，非线性温度分布夹芯板的临界热屈曲温度最大。

图8给出了铺设方式为[θ/θ1/Core/θ1/θ]，长厚比a/h=20，hp/h=0.100，均匀温度分布下夹芯板的临界热屈曲温度随纤维角度的变化情况。从图中可以看出整体临界热屈曲温度呈现对称变化。从图8(a)中可以看出，当正方形夹芯板的纤维角度θ在0°到45°之间，[θ/0°/Core/0°/θ]铺层方式夹芯板的临界热屈曲温度最小，[θ/45°/Core/45°/θ]铺层方式夹芯板的临界热屈曲温度最大；当纤维角度θ在45°到90°之间，[θ/90°/Core/90°/θ]铺层方式夹芯板的临界热屈曲温度最小，[θ/45°/Core/45°/θ]铺层方式夹芯板的临界热屈曲温度最大。从图8(b)中可以看出，对于长方形夹芯板，[θ/0°/Core/0°/θ]铺层方式夹芯板的临界热屈曲温度先增大后减小而且当纤维角度θ为90°时达到最大值；当纤维角度θ为75°或105°时，[θ/45°/Core/45°/θ]铺层方式夹芯板的临界热屈曲温度达到最大，纤维角度θ为0°或180°时最小；当纤维角度θ为45°或135°时，[θ/90°/Core/90°/θ]铺层方式夹芯板的临界热屈曲温度达到最大，纤维角度θ为90°时最小。因此，夹芯板的铺设方式对夹芯板临界屈曲温度的最大值所对应的纤维角度有很大的影响。

图7 临界热屈曲温度随纤维角度的变化情况Fig.7 Critical thermal buckling temperature difference vs. fiber angle θ

图8 不同铺设方式下临界热屈曲温度随纤维角度的变化情况Fig.8 Critical thermal buckling temperature difference vs. fiber angle θ under different layer way

4 结论

本文基于三角剪切变形理论，求解了夹芯板的临界热屈曲温度。讨论了温度函数指数、边界条件、长厚比、长宽比、hp/h和铺层纤维角度对夹芯板临界热屈曲温度的影响。随着温度函数指数β的增大夹芯板的临界热屈曲温度逐渐增大。夹芯板的临界热屈曲温度随着长厚比、hp/h的增大而减小。由于固支边界的约束比简支边界的约束强，因此，四边固支边界夹芯板的临界热屈曲温度大于四边简支边界夹芯板的临界热屈曲温度。混合边界夹芯板临界热屈曲温度的变化情况与边界所对应的边长有关。不同长宽比夹芯板热临界屈曲温度的最大值对应的纤维角度不同。不同铺设方式夹芯板临界热屈曲温度的最大值对应的纤维角度不同。

附录A式(5)和式(6)的展开式

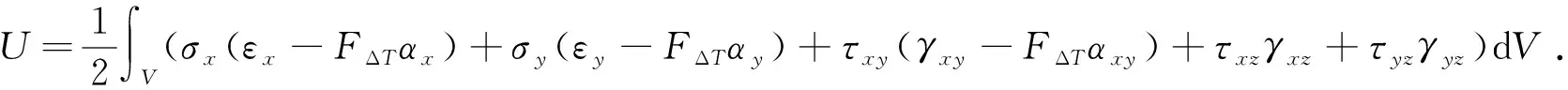
附录B式(7)的表达式

式中：

式中：

式中：