计及齿轮时变啮合刚度的机车驱动系统振动稳定性

王 燕，刘建新，李 淼

(1.西南交通大学 机械工程学院，成都 610031；2.西南交通大学 牵引动力国家重点实验室，成都 610031；3.中车株洲电力机车研究所有限公司，湖南 株洲 412001)

计及齿轮时变啮合刚度的机车驱动系统振动稳定性

王 燕1，刘建新2，李 淼3

(1.西南交通大学 机械工程学院，成都 610031；2.西南交通大学 牵引动力国家重点实验室，成都 610031；3.中车株洲电力机车研究所有限公司，湖南 株洲 412001)

针对齿轮时变啮合刚度激励的机车驱动系统振动问题，基于势能原理获得了齿轮时变啮合刚度，并用傅里叶级数展开，采用“黏着系数-蠕滑速度”经验公式描述具有负斜率特性的轮轨黏着力，建立了驱动系统扭转振动和轮对纵向振动的耦合模型。在系统振动微分方程的平衡位置处对其进行线性化处理，进而利用多尺度法获得了系统振动稳定的边界条件，并进行了数值仿真验证和参数影响分析。分析结果表明：增大被动齿轮与主动齿轮的等效惯量比、轮对与构架的质量比有助于增强机车驱动系统的稳定性；当机车速度接近119/j(km·h-1)(j=1，2，3，…) 时，由于齿轮时变啮合刚度的作用，驱动系统会产生参数共振；且当速度接近119 km·h-1时，系统产生参数共振的区域较广，且啮合阻尼在[0，1×104]N·s·m-1范围内变化时，对系统参数共振区域的范围影响很小，机车应尽量避免以该速度行驶。

机车；驱动系统；时变啮合刚度；多尺度法；稳定性

机车驱动系统主要由牵引电机、传动装置和轮对构成。传动装置一般为齿轮传动，其主要功能是将牵引电机的驱动力有效地传递至轮对，进而通过轮轨接触界面的黏着形成牵引力以实现机车的纵向运动。齿轮啮合时，由于同时参与啮合的轮齿数和啮合位置的变化，导致齿轮啮合刚度具有周期时变特性，该特性已得到Wan等[1-4]的高度关注。在齿轮时变啮合刚度激励下，机车驱动系统的振动响应有时可能较弱，但在一定条件下也可能出现剧烈的共振现象。系统是否发生共振现象，取决于系统在对应条件下的稳定性。王建军等[5-6]针对考虑时变啮合刚度的齿轮系统的稳定性进行了大量的研究。然而，考虑机车齿轮时变啮合刚度激励的影响，针对机车驱动系统振动稳定性的研究工作仍较为少见。同时，运用中发现，机车在运行中驱动系统存在异常振动。因此，开展齿轮时变啮合刚度激励下机车驱动系统的振动研究，明确系统振动稳定产生的条件，对机车的安全运行具有重要的意义。

基于此，本文基于势能原理获得了齿轮时变啮合刚度，并用傅里叶级数展开，采用“黏着系数-蠕滑速度”经验公式描述具有负斜率特性的轮轨黏着力，建立了驱动系统扭转振动和轮对纵向振动的耦合模型。利用多尺度法推导了系统振动稳定产生的条件，数值模拟了系统的振动响应，并获得了系统参数对振动稳定性的影响规律。

1 机车驱动系统的动力学分析模型

图1(a)和图1(b)分别为轴悬式机车驱动系统和架悬式机车驱动系统模型[7]，考虑主动、被动齿轮啮合时的时变刚度，建立如图2所示的机车驱动系统的动力学分析模型。符号Ii、Ri、θi、Ti分别为主动(i=1)、被动(i=2)齿轮上的等效转动惯量、基圆半径、转动角位移和施加的转矩；km(t)、cm分别为齿轮啮合刚度与阻尼；mi、xi、Fi分别为轮对(i=1)、构架(i=2)上的等效质量、纵向位移和所施加的力；kx、cx分别为纵向刚度与阻尼；r为车轮半径。牵引电机的驱动力矩T1施加在主动齿轮上驱动其转动，被动齿轮则固接在轮轴上并在轮齿啮合力的作用下转动，轮对的转动使轮轨接触界面产生黏着力F1，进而实现轮对的纵向运动。

(a) 轴悬式驱动系统

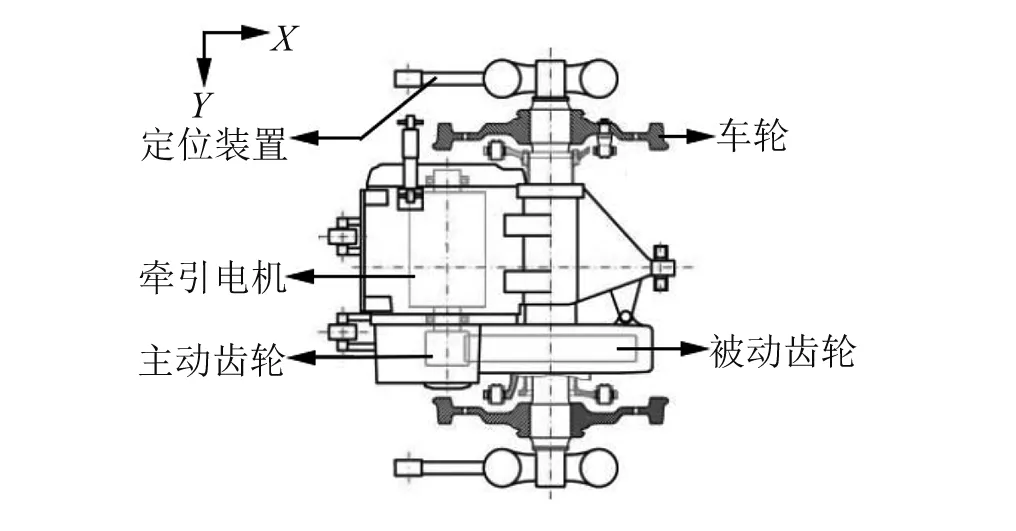
(b) 架悬式驱动系统图1 机车驱动系统模型Fig.1 Locomotive driving system model

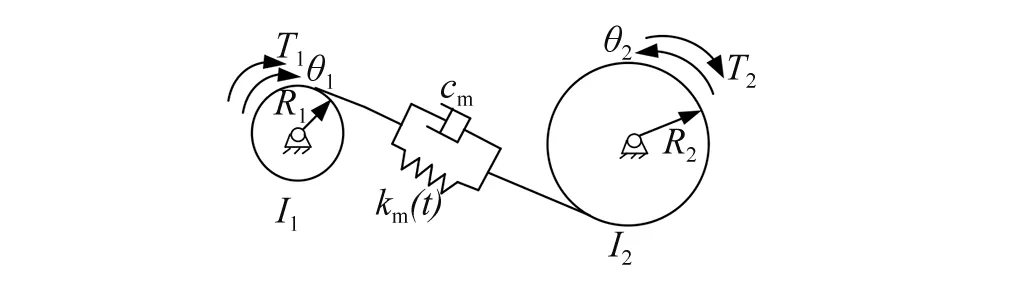
(a) 驱动系统扭转振动

(b) 轮对纵向振动图2 机车驱动系统的动力学分析模型Fig.2 Dynamic analysis model of locomotive driving system

1.1 动力学方程

根据图2所示的动力学分析模型，建立相应的动力学方程

(1)

式中，T2=rF1。令Δx=R1θ1-R2θ2，Δy=x1-x2，且令去除系统平衡位置后对应的值分别为x、y，则式(1)经过变换后可得

(2)

1.2 齿轮时变啮合刚度

齿轮啮合时参与啮合的轮齿对数随时间呈现周期性往复交替变化，导致齿轮啮合刚度亦呈现时变周期性。将齿轮时变啮合刚度表示为关于主动齿轮转动角位移θ1(单位°)的傅里叶级数的形式

(3)

式中：k0为啮合刚度的平均值；kj为Fourier级数的系数；φj为相位角；wn=2π/T，T=360/Z1，Z1为主动齿轮齿数。

进而通过变换得到齿轮时变啮合刚度关于时间的傅里叶级数形式为

(4)

式中，we=2πZ1n1/60， n1为主动齿轮转数，r·min-1。

1.3 轮轨黏着力

轮轨黏着系数的大小与轮轨蠕滑率或蠕滑速度紧密相关。本文采用日本新干线的“黏着系数-蠕滑速度”经验公式[8]

u(vs)=a·exp(-3.6bvs)-c·exp(-3.6dvs)

(5)

式中：u(vs)为轮轨黏着系数；vs为轮轨蠕滑速度，m·s-1；a、b、c、d为反映轮轨接触状态的参数。

当a=0.53、b=0.12、c=0.53、d=2.40[9]时，得到黏着系数及其关系曲线斜率ku关于蠕滑速度的变化曲线如图3所示。

图3 黏着系数及其斜率关于蠕滑速度的关系曲线Fig.3 Relation curve of adhesion coefficient and its slope on creep speed

轮轨黏着力F1=u(vs)Q。其中Q为机车轴重，N。

1.4 方程的无量纲化

轮轨蠕滑速度vs用图2中的符号表示为

(6)

令平衡位置处的蠕滑速度为vs0，可得

(7)

令x=bxe，y=bye，(b为特征尺寸)，整理式(2)可得

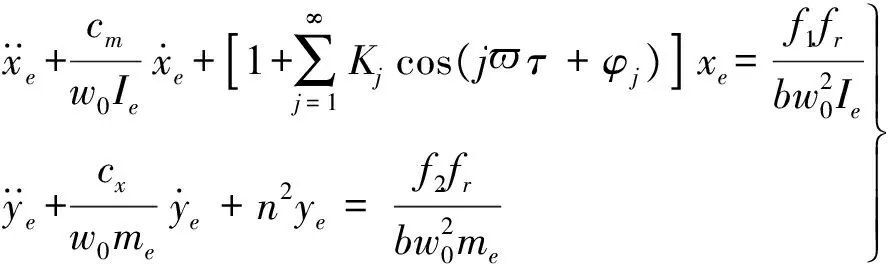
(8)

2 机车驱动系统振动稳定性分析

为给出驱动系统振动稳定性的条件，将式(8)中的fr在vs0附近进行线性化处理，表示为

(9)

将式(9)代入式(8)，整理可得

(10)

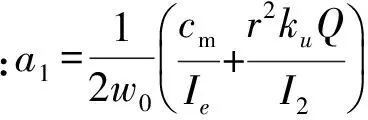
引入小参数ε(0<ε<1)， 令ai=εμi， (i=1，2，3，4)，Kj=εkej，整理式(10)可得

(11)

利用多尺度法[10-11]进行计算，设式(11)的近似解为

(12)

式中：T0=τ；T1=ετ。

将式(12)代入式(11)，展开后令ε的同次幂的系数为0，得到零次和一次近似方程分别为

(13a)

(13b)

将式(13a)的解写为

(14)

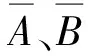
将式(14)代入式(13b)，整理可得

(15)

式中，cc为前面各项的共轭复数。

不考虑n趋近于1时的情况，对以下两种情况进行分析

(16)

令A=A1(T1)+iA2(T1)，B=B1(T1)+iB2(T1)，分离实部与虚部后得到对应的特征方程为

16n2(λ+μ1)(λ+μ3)=0

(17)

所以，此时系统振动稳定的条件为：a1>0且a3>0。

(18)

设A=[A1(T1)+iA2(T1)]e(ijσT1+iφj)/2，B=B1(T1)+iB2(T1)。分离实部与虚部后得到对应的特征多项式为

(19)

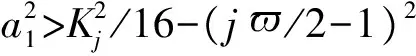
3 数值仿真分析

以某型机车为实例，其齿轮副的主要参数为：主动齿轮齿数Z1=32，被动齿轮齿数Z2=75，模数m=12，压力角a=22.5°。基于势能原理[12-13]，综合考虑轮齿弯曲变形、剪切变形、轴向压缩变形、赫兹接触变形、以及轮体变形对应的啮合线上的等效刚度。其中，前4种变形对应的等效刚度的计算参见文献[14]，轮体变形对应的等效刚度的计算参见文献[15-16]。进而获得齿轮综合时变啮合刚度，并将其展开为傅里叶级数形式，结果如图4所示。其中kj(j=0，1，…，8)的值见表1所示。

表1 啮合刚度各阶谐波幅值

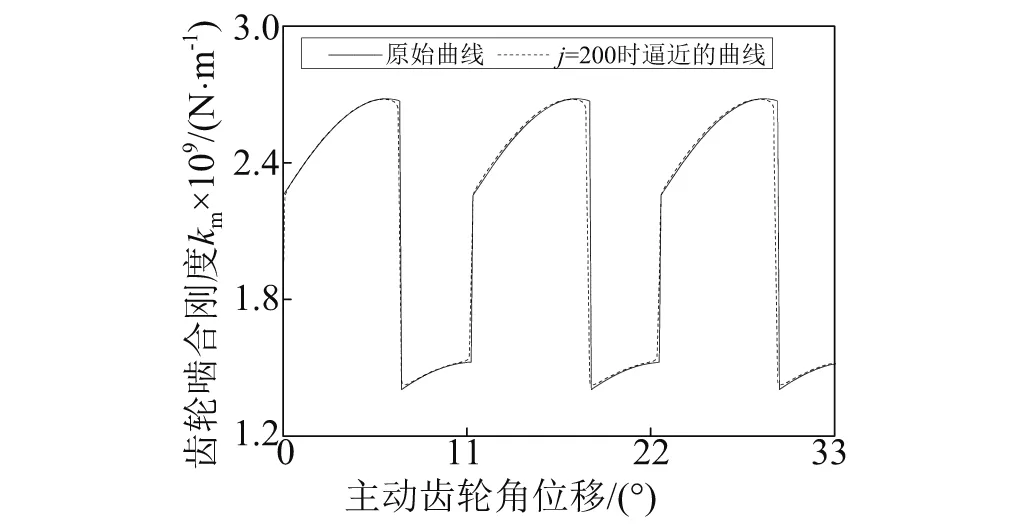
图4 齿轮啮合时变刚度Fig.4 Time-varying mesh stiffness of gears

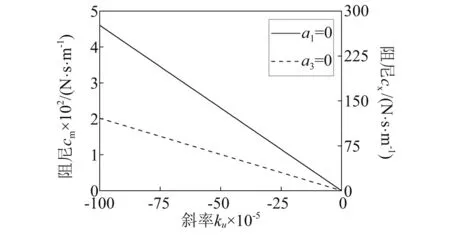
图5 a1=0、a3=0时的临界稳定曲线Fig.5 Critical stability curve when a1=0、a3=0

3.1 驱动系统振动稳定性的数值仿真验证

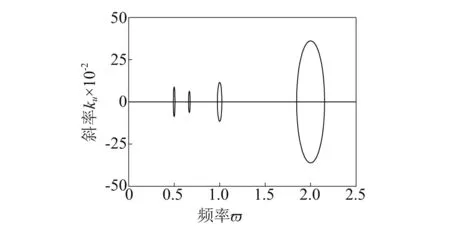
(a) j=1～4

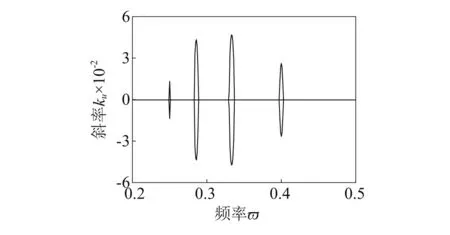
(b) j=5～8图6 参数共振时的临界稳定曲线Fig.6 Critical stability curve when parametric resonance occurs

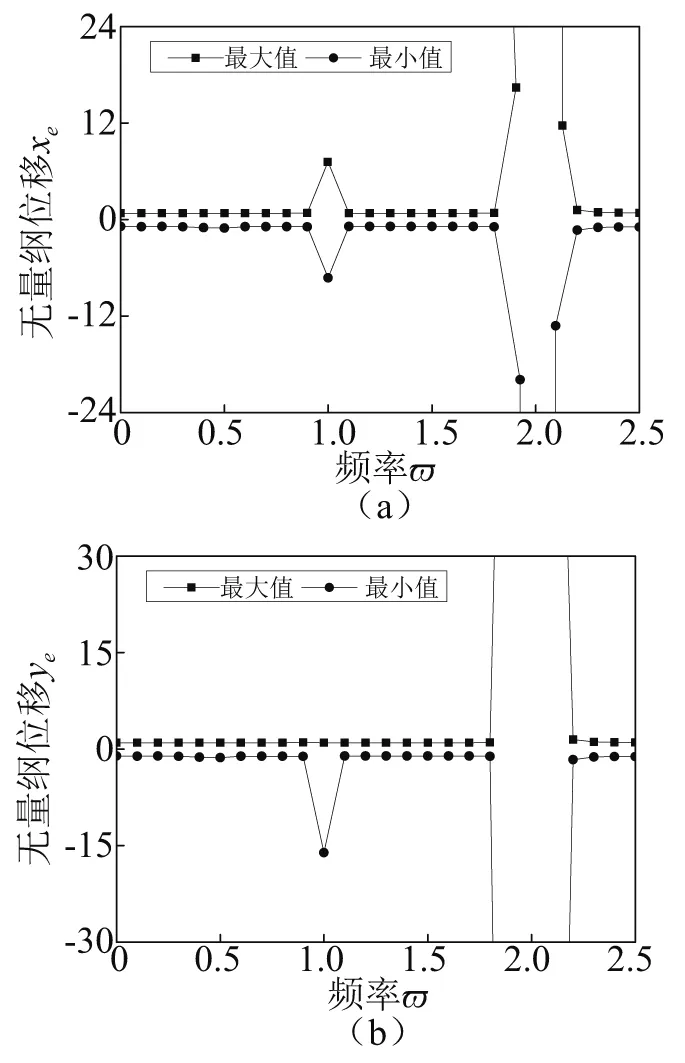
图7 不同下系统振动位移的最大值与最小值Fig.7 Maximum and minimum values of vibration displacement under different

图8 vs0=0.3 m·s-1，=1.55Fig.8 Vibration response when vs0=0.3 m·s-1，=1.55

图9 vs0=0.5 m·s-1，=1.55Fig.9 Vibration response when vs0=0.5 m·s-1，=1.55

3.2 驱动系统振动稳定性的参数影响分析

令等效惯量比N1=I2/I1、等效质量比N2=m1/m2，利用推导出的稳定条件式，仿真得到不同参数下机车驱动振动的临界稳定曲线如图10～图12所示。

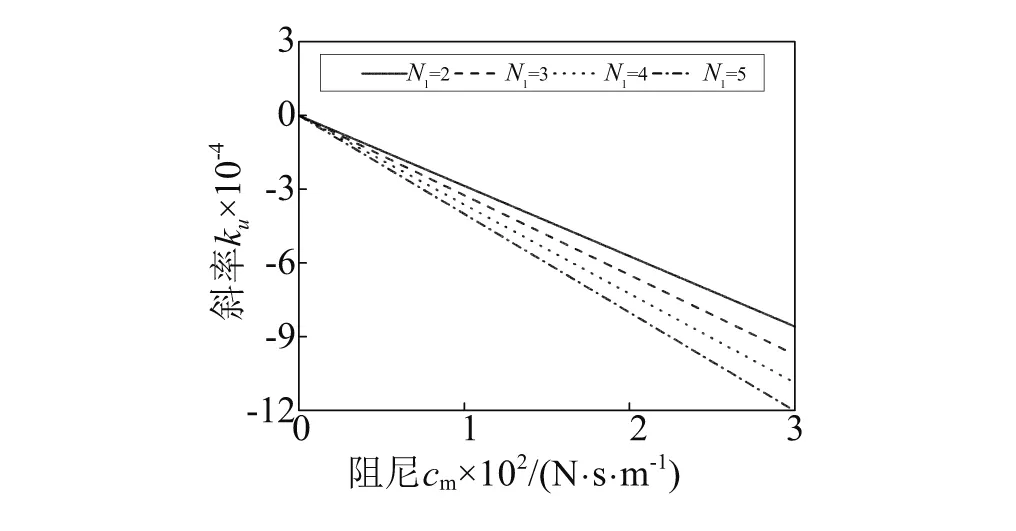
图10 a1=0时的临界稳定曲线Fig.10 Critical stability curve when a1=0

图11 a3=0时的临界稳定曲线Fig.11 Critical stability curve when a3=0

图12 参数共振(j=1)时的临界稳定曲线Fig.12 Critical stability curve when parametric resonance occurs (j=1)

当阻尼cx=100 N·s·m-1时，得到a1=0时ku-cm平面上的临界稳定曲线如图10所示。由图10可知，等效惯量比N1越大，系统稳定区域越广。当阻尼cm=100 N·s·m-1时，得到a3=0时ku-cx平面上的临界稳定曲线如图11所示。由图11可知，等效质量比N2越大，系统稳定区域越广。所以，增大等效惯量比N1、质量比N2有利于增强系统的稳定性。

4 结 论

本文考虑了齿轮啮合刚度的时变特性，建立了机车驱动系统扭转振动和轮对纵向振动的耦合模型，利用多尺度法推导了系统振动稳定的条件，并进行了数值仿真验证和参数影响分析。结果表明多尺度法推导出的系统振动稳定的条件与数值仿真模拟系统的振动响应具有良好的一致性。通过分析获得结论如下：

(1) 增大被动齿轮与主动齿轮的等效惯量比、轮对与构架的质量比有利于增强机车驱动系统的稳定性。

(2) 由于齿轮时变啮合刚度的作用，当机车速度约119/j(km·h-1)(j=1，2，3，…) 时，机车驱动系统会产生参数共振。

(3) 当速度约119 km·h-1时，啮合阻尼在[0，1×104]N·s·m-1范围内变化时，对系统参数共振区域的范围影响很小，且此时黏着系数曲线斜率在[-0.35，0.35]范围内变化时，系统均会产生参数共振，机车运营中应给予避免。

[ 1 ] WAN Zhiguo， CAO Hongrui， ZI Yanyang，et al.An improved time-varying mesh stiffness algorithm and dynamic modeling of gear-rotor system with tooth root crack[J].Engineering Failure Analysis，2014，42(5)：157-177.

[ 2 ] CHEN Zaigang ， SHAO Yimin. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J]. Mechanism and Machine Theory， 2013，62(4)：63-74.

[ 3 ] PANDYA Y， PAREY A.Simulation of crack propagation in spur gear tooth for different gear parameter and its influence on mesh stiffness[J].Engineering Failure Analysis，2013，30：124-137.

[ 4 ] DEL RINCON A F， VIADERO F， IGLESIAS M，et al.A model for the study of meshing stiffness in spur gear transmissions[J]. Mechanism and Machine Theory，2013，61：30-58.

[ 5 ] 王建军，李其汉，李润方.齿轮系统非线性振动研究进展[J].力学进展， 2005，35(1)： 37-51. WANG Jianjun， LI Qihan， LI Runfang.Research advances for nonlinear vibration of gear transmission systems[J]. Advance in Mechnics， 2005， 35(1)： 37-51.

[ 6 ] 张微，丁千.直齿圆柱齿轮啮合耦合振动系统参数振动研究[J].工程力学，2015，32(5)： 213-220. ZHANG Wei，DING Qian.Research on properties for parametric vibration of a spur gear meshing and coupling system[J]. Engineering Mechanics， 2015，32(5)：213-220.

[ 7 ] YAO Yuan， ZHAO Shiyin， XIAO Feixiong，et al.The effects of wheelset driving system suspension parameters on the re-adhesion performance of locomotives[J].Vehicle System Dynamics，2015，53(12)：1935-1951.

[ 8 ] TAKAOKA Y， KAWAMURA A. Disturbance observer based adhesion control for shinkansen[C]//IEEE 6th International Workshop on Advanced Motion Control. New York：IEEE，2000：169-174.

[ 9 ] LIU Jianxin， ZHAO Huaiyun， ZHAI Wanming.Mechanism of self-excited torsional vibration of locomotive driving system[J]. Frontiers of Mechanical Engineering in China，2010，5(4)：465-469.

[10] THEODOSSIADES S， NATSIAVAS S. Non-linear dynamics of gear-pair systems with periodic stiffness and backlash[J]. Journal of Sound and Vibration，2000，229(2)：287-310.

[11] 刘延柱，陈立群.非线性振动[M].北京：高等教育出版社，2001.

[12] LIANG Xihui， ZUO M J， PANDEY M.Analytically evaluating the influence of crack on the mesh stiffness of a planetary gear set[J].Mechanism and Machine Theory，2014，76(6)： 20-38.

[13] MA Hui， SONG Rongze， PANG Xu， et al. Time-varying mesh stiffness calculation of cracked spur gears[J].Engineering Failure Analysis，2014，44(5)：179-194.

[14] TIAN Xinhao， ZUO M J， FYFE K R. Analysis of the vibration response of a gearbox with gear tooth faults[C]//ASME 2004 International Mechanical Engineering Congress and Exposition.Anaheim：American Society of Mechanical Engineers，2004：785-793.

[15] SAINSOT P， VELEX P， DUVERGER O.Contribution of gear body to tooth deflections—a new bidimensional analytical formula[J]. Journal of Mechanical Design，2004，126(4)：748-752.

[16] CHEN Zaigang， SHAO Yimin. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth[J]. Engineering Failure Analysis，2011，18(8)：2149-2164.

Vibration stability for a locomotive driving system with time-varying mesh stiffness of gears

WANG Yan1，LIU Jianxin2， LI Miao3

(1. Faculty of Mechanical Engineering， Southwest Jiaotong University， Chengdu 610031，China；2. State Key Laboratory of Traction Power ，Southwest Jiaotong University， Chengdu 610031， China；3. CRRC Zhuzhou Institute Co.， Ltd.， Zhuzhou 412001， China)

Aiming at the vibration problem of a locomotive driving system with time-varying mesh stiffness of gears， torsional vibration of the driving system and longitudinal vibration of wheelsets were established. In the model， mesh stiffness was obtained based on the potential energy principle and expressed using the technique of Fourier series. Wheel/rail adhesion force with the characteristic of negative slope was described by a formula of adhesion coefficient and creep speed. Based on this model， the vibration differential equation was linearized at the balance point. The boundary condition of the stable system was gained by using the method of multiple scales. In order to verify the calculated result， the numerical simulation was carried out. At the same time， the influence of parameters on the stability of the driving system was analyzed. The results reveal that increasing the equivalent inertia ratio of driving gear and driven gear， mass ratio of wheelsets and frame is helpful to enhance the stability of the driving system. Parametric resonance occurs as locomotive speed is close to 119/j(km·h-1)(j=1，2，3，…) because of the time-varying mesh stiffness. When speed approaching 119 km·h-1， the parametric resonant region is wide. At this speed， mesh damping changes within [0，1×104]N·s·m-1is little helpful to the change the resonant region of the system. The locomotive should try to avoid traveling at this speed.

locomotive； driving system； time-varying mesh stiffness； method of multiple scales； stability

国家自然科学基金(51375403)；中央高校基本科研业务专项科技创新(2682015ZD12)

2016-05-03 修改稿收到日期： 2016-06-16

王燕 女，博士生，1989年出生

刘建新 男，博士，教授，博士生导师，1965年出生

U260

A

10.13465/j.cnki.jvs.2017.16.016