压电柔性机械臂的实验辨识及最优极点配置抑振控制

2017-08-31娄军强廖江江李国平杨依领魏燕定

振动与冲击 2017年16期

娄军强, 廖江江, 李国平, 杨依领, 魏燕定

(1.宁波大学机械工程与力学学院浙江省零件轧制成形技术研究重点实验室, 浙江宁波 315211；2.浙江大学机械工程学院浙江省先进制造技术重点实验室, 杭州 310027)

娄军强1, 廖江江1, 李国平1, 杨依领2, 魏燕定2

研究了压电柔性臂系统的实验辨识和基于极点配置法的振动主动控制问题。针对粘贴应变传感器和压电致动器的压电柔性臂系统，提出了零点重新分布的理论传递函数模型。通过扫频实验采用频域辨识方法确立了从压电致动器控制电压输入到应变桥路电压输出的实验传递函数模型，辨识模型与实际结构响应吻合程度达94.8%。并通过多频激励实验证实了辨识模型与实际结构具有较高的一致性。利用辨识得到的传递函数模型建立了系统状态方程表达式，提出了一种移动距离最短、满足系统闭环阻尼要求的闭环极点位置确立方法。不同闭环极点下的数值仿真和实验结果均证明了采用的最优极点配置方法的有效性。实验结果表明，柔性臂在特定激励和外界干扰激励下产生的弹性振动均得到了有效抑制。所提出的模型辨识方法和极点配置策略是可行的。

压电柔性臂；系统辨识；最优极点配置；振动主动控制

由于具有质量轻、发射成本低、能耗低且操作灵活方便等优点，以大跨度轻质太空臂杆、大型柔性天线以及太阳能帆板等为代表的柔性构件在空间机械臂、太空机器人以及航天器的设计和制造领域得到了广泛应用[1-2]。但是结构柔性及振动对柔性结构的定位精度和操作效率具有较大影响，在某些极端情况下甚至导致整个系统失稳[3]。因此柔性结构的振动抑制是一项具有挑战性的课题，并引起了国内外研究学者的广泛关注[4]。

以压电陶瓷材料为代表的智能材料具有易与被控结构集成为一体的优势，基于压电材料开展柔性结构的振动主动控制研究是目前的研究热点[5-6]。经典的反馈控制方法不需要额外的参考信号，并可以通过降低系统灵敏度的方法削弱系统参数变化带来的影响，具有一定的鲁棒性，故在柔性结构的振动主动控制技术中仍发挥着巨大作用[7]。直观简单、物理意义明确的极点配置(Poles Assignment, PA)控制技术就是其中一种。设计者可以灵活方便地将系统极点配置在期望位置从而达到预期控制效果[8]。Sethi等[9]成功地将极点配置法用于3.5 m长的工形梁建筑结构的振动主动控制中。针对压电柔性梁结构，Sethi等[10]进一步通过灵敏度分析重新配置系统闭环极点，有效抑制了柔性梁的多阶模态振动。Rahman等[11]将极点配置法用于压电柔性板结构的振动主动控制技术中，取得了不错的控制效果。Kuo等[12]结合映射理论、Kharitonov定理和Routh-Hurwitz判据提出将柔性臂系统的极点配置在特定的三角区域，提高了控制系统的鲁棒性和稳定性。但是现有的极点配置法在极点配置位置的选取上具有一定的随意性，没有形成较规范的配置准则。如果能够结合实际寻找一种简单、有效的极点配置方法，将控制系统闭环极点放置在合适位置，势必可以取得更好的控制效果。

另一方面，控制器的设计与系统动力学模型的精度密切相关。在关于柔性结构理论模型的研究中，以常微分方程表示的系统动力学模型是常见形式[13]。但是由于压电致动器/传感器的加入，很多时候智能柔性结构系统的微分方程是很难建立的。基于有限元分析法得到的数值近似模型更加实际可行[14]。但是在数值近似模型的建立过程中也存在着很多假设：如假定压电致动器与柔性结构完美粘贴，不考虑黏结层的厚度等[15]，而且实际结构的性能参数也不可能与标称值完全一致。考虑到这些不利因素，采用实验辨识的方法建立智能柔性结构的动力学模型显然是一种精度更高、效果更好的建模方法。

本文针对压电柔性结构的振动主动控制问题，首先介绍了所涉及的压电柔性臂实验系统。提出了零点重新分布的系统传递函数模型，并通过扫频实验建立了从压电致动器控制电压输入到柔性臂根部应变桥路输出的传递函数模型，验证并确立了压电柔性臂系统的实验辨识模型。利用得到的辨识模型建立了系统状态方程表达式，基于极点配置(PA)法设计了移动距离最短、满足系统闭环阻尼要求的闭环极点位置。最后通过仿真和实际实验验证了相关的建模方法和控制策略的有效性。

1 系统描述

本文所涉及的压电柔性臂系统如图1所示。柔性臂为悬臂形式，一端固定在夹持端、一端自由。在柔性臂的上下表面对称地贴有两组应变片传感器组成全桥电路用于检测柔性臂结构的振动；在柔性臂的两侧表面对称地粘贴压电陶瓷片作为致动器用于激励或抑制柔性臂的弹性振动。为了获得较好的应变检测和振动抑制效果，传感器和致动器都布局在柔性臂的根部位置。同时在柔性臂的末端安装有激光位移传感器用于实时检测柔性臂末端的振动位移。

图1 压电柔性臂系统结构图Fig.1 Block diagram of the flexible manipulator system

系统测试中，利用应变传感器(阻值350 Ω，灵敏度系数2.08，桥压 4 V)组成的全桥电路检测柔性臂的振动，桥路输出电压信号经动态应变仪(型号：AFT-095，放大增益5 000)调理为-10～+10 V的电压信号，并利用巴特沃斯低通滤波器(截止频率100 Hz)滤波，最后经多通道数据采集卡(型号：NI PCI-6221(37pin))的A/D模块输送到计算机中。压电致动器的控制电压信号通过数据采集卡的D/A模块输出(-5～+5 V)，经压电陶瓷驱动电源(型号：HPV-1C0150A0300D，增益15)放大为-75～+75 V的电压信号，作用在压电致动器上，激励压电致动器按照设定的控制律实现柔性臂的振动控制。激光位移传感器(型号：米铱 ILD 1402-50(027))输出柔性臂末端的振动位移经调理电路转换为1～5 V的电压信号，经数据采集卡A/D模块输送到计算机中。整个测控系统基于NI-LABVIEW平台完成，系统实物装置如图2所示。

图2 压电柔性臂测控系统实物图Fig.2 Experimental setup of the flexible manipulator system

2 系统模型辨识

2.1 理论模型

柔性臂和压电致动器的基本参数如表1所示。建立系统的数学模型是进行实验辨识的前提，如果将柔性臂视为简单的欧拉-伯努利梁模型，则粘贴有压电致动器的柔性臂结构传递函数表达式为

(1)

式中：ki为开环增益；ξi为第i阶振动模态阻尼；ωi为第i阶振动模态的角频率。

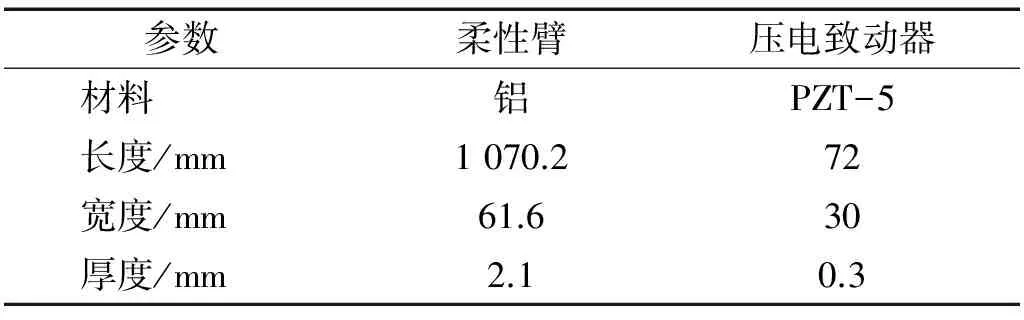
表1 柔性臂和压电致动器的基本参数

事实上，想要精确得到柔性臂的无穷阶振动模态是不可能的。而在实际中，我们往往只需要关注柔性臂在某一特定频带内的振动特性，故可引入模态截断技术，只保留一定频率范围内的振动模态。为了抵消忽略高阶模态带来的模态截断效应，Qrszulik等[16]提出了添加馈通环节的降阶传递函数模型

(2)

式中：n为保留的模态阶数；D为馈通环节系数。

虽然式(2)得到的降阶模型中系统极点仍位于正确的位置，即保证固有频率不变，但此做法仍然导致系统能量分布的改变，从而使得到的降阶模型闭环特性与实际结构存在一定差异，严重时甚至导致系统在闭环控制时出现不稳定的现象。为了避免此类现象，可重新构造每阶模态的零点分布，得到降阶模型为

(3)

式中，ai,bi为重新分布的第i阶模态零点。

2.2 实验辨识

在实验辨识过程中，利用测量得到的系统开环频率响应函数(Frequency Response Function, FRF)辨识得到压电柔性臂系统的传递函数模型。由于柔性臂的一阶振动模态在其振动中起主导作用，故此处仅截取其一阶模态进行辨识研究。实验辨识中采用一个幅值为5 V，频率范围为0～32 rad/s的正弦扫频信号作用到压电致动器上，激励起柔性臂的一阶弹性振动，并使用应变全桥电路检测柔性臂的振动，整个扫频过程持续15 s，采样频率为100 Hz，实验中激励信号和应变电桥输出信号如图3所示。

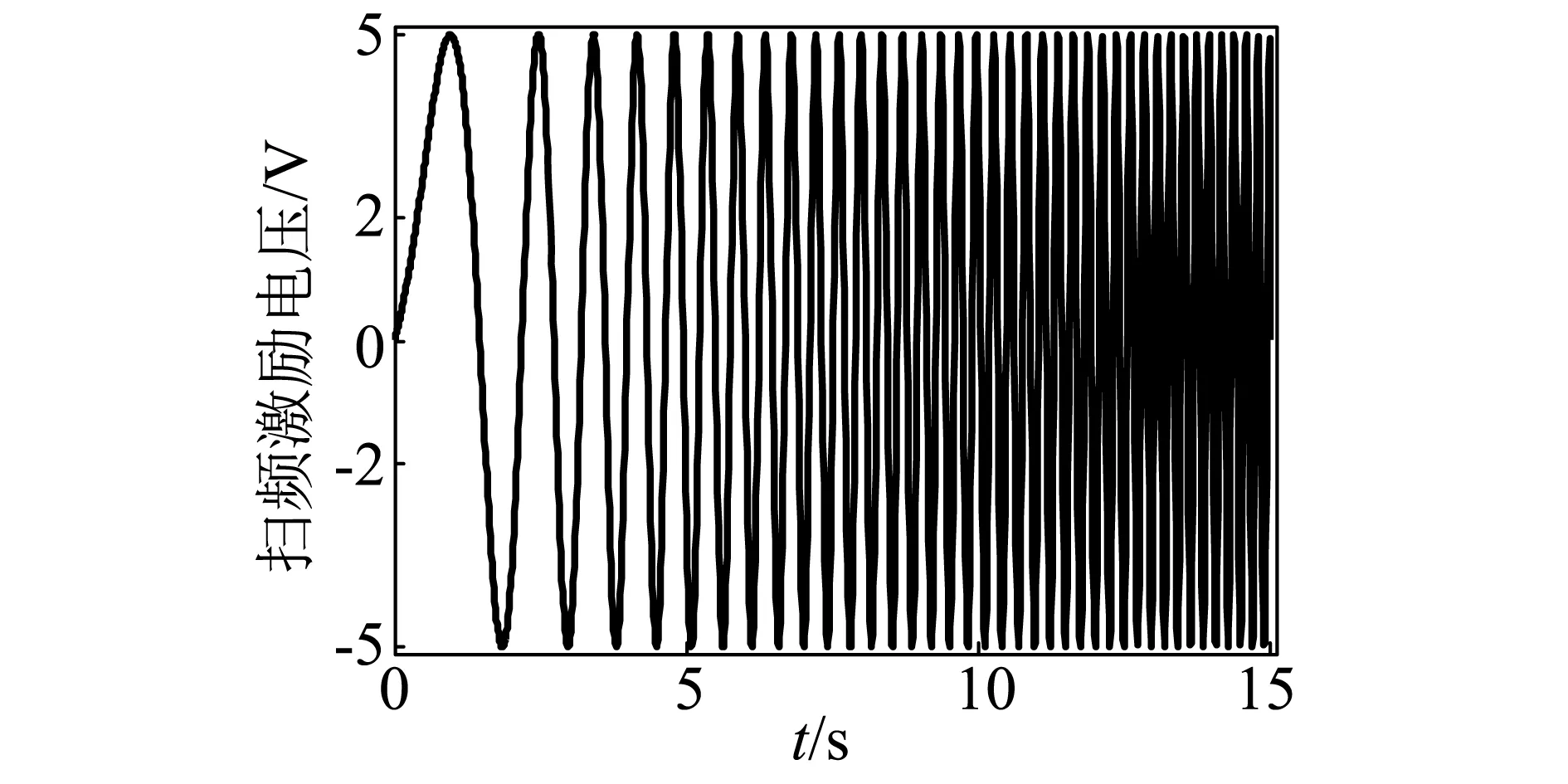
(a) 扫频激励电压信号

(b)应变输出电压信号图3 扫频实验结果Fig.3 Experimental results by the chirp excitation

对输入激励电压信号u(t), 应变输出电压信号y(t)分别进行Fourier变换并进行运算，即可得到压电柔性臂系统的实测开环频率响应函数

(4)

式中：Suy(jω)为输入信号u(t)与输出信号y(t)的互功率谱密度函数；Suu(jω)为输入信号u(t)的自功率谱密度函数。

扫频信号激励下压电柔性臂系统的实测开环频率响应函数曲线如图4所示。从图可以看出扫频实验激起了柔性臂的一阶振动模态，其一阶固有频率在9.2rad/s(1.46Hz)附近。

在保留柔性臂一阶振动模态的基础上，加入馈通环节，基于式(2)所示模型进行实验辨识，利用Matlab的系统辨识工具箱，可以得到压电柔性臂系统的传递函数模型为

图4 实测开环频率响应函数曲线Fig.4 Measured open-loop frequency response curve

(5)

为了比对实验辨识结果，利用式(3)所示传递函数模型对压电柔性臂结构进行辨识，同样利用Matlab的系统辨识工具箱，可以得到零点重新分布模型见式(6)

(6)

由于辨识模型Gd(s)和G(s)分母对应项的系数完全相同，故两个模型具有相同的固有频率和阻尼比。在图3(a)所示的扫频信号激励下，图5(a)给出了不同辨识模型的开环频响函数曲线，图5(b)则进一步给出了各模型对应的时域输出信号，并与实测的实验数据进行对比。无论从系统频响函数曲线还是时域输出曲线的对比结果都可以清晰看出：零点重新分布的辨识模型G(s)与实际系统响应具有较高的吻合度，其时域输出和频响曲线与实际结构响应基本一致。而加上馈通环节的传递函数模型Gd(s)虽然在固有频率处与实际结构的频率响应基本重合，但是对实际结构低频响应特性的刻画却存在着一定程度的失真，从图5(b)中可以看出在扫频信号激励的最初阶段，辨识模型Gd(s)与实际结构的时域输出存在着明显偏差。显然忽略的高阶模态响应导致了此现象的发生，而G(s)模型通过零点重新分布调整了系统的能量分布，故更加精确地估计了系统的动力学响应，得到了更好的辨识结果。

(a) 频率响应函数曲线

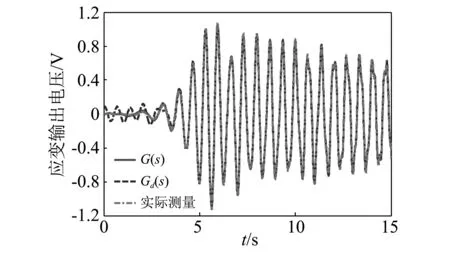
(b) 应变输出电压信号

两个辨识模型Gd(s)和G(s)的零极点分布情况如图6所示。可以看出两个辨识模型的极点完全重合，而二者的零点却完全不同，显然由于高阶模态的截断效应导致降阶模型的零点重新分布，而基于零点重新分布的辨识模型更好地补偿了模态截断效应。

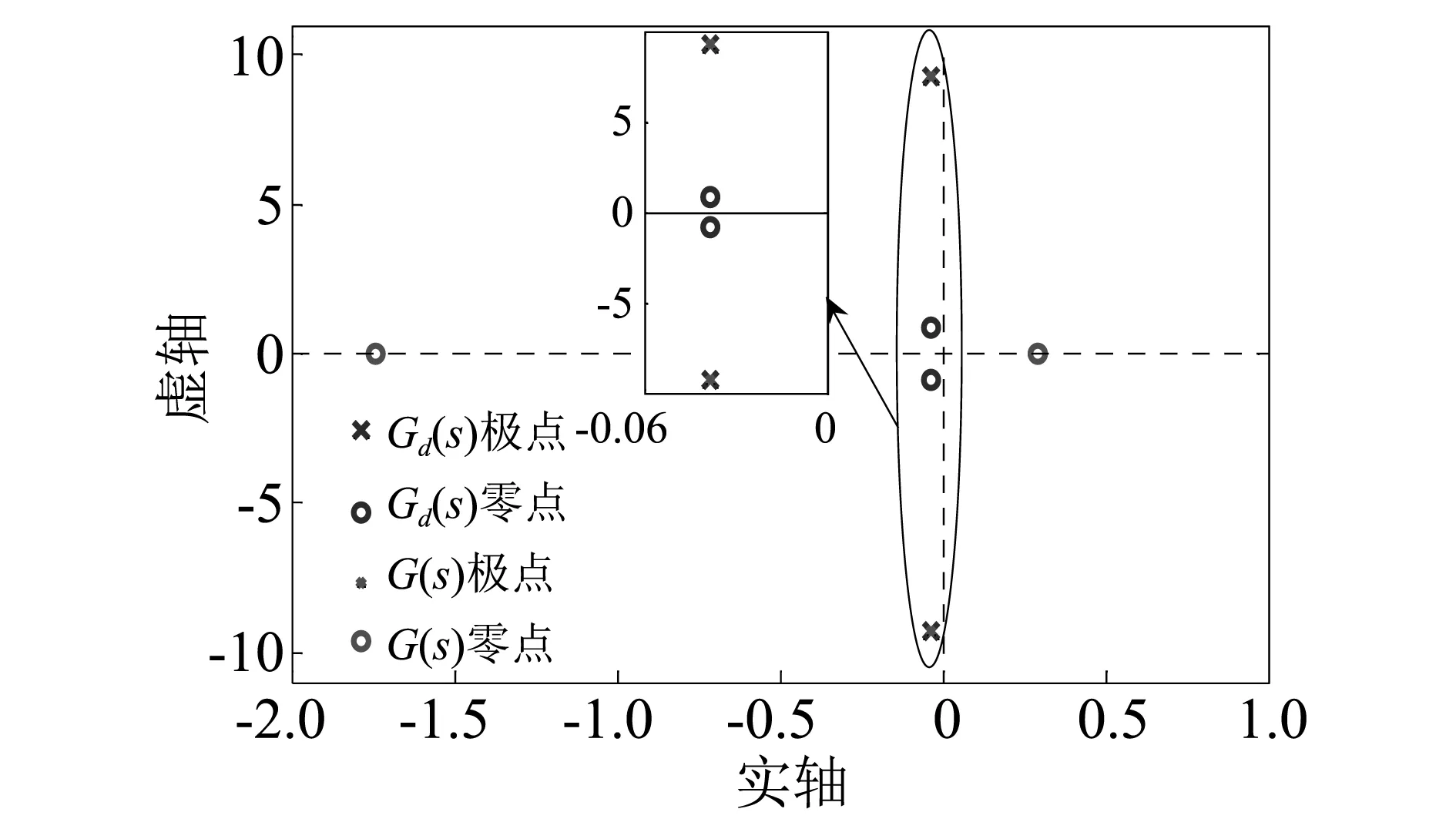
图6 辨识模型的零极点分布图Fig.6 Locations of poles and zeros for the identified models

为了进一步检验辨识得到的传递函数模型与实际结构的吻合程度，图7给出了辨识得到的模型与实际结构在另一个输入信号激励下的输出比对结果。在模型验证实验中，给压电柔性臂系统施加一多个频率信号组成的多频激励信号，其具体表达式为

uva(t)=2[sin(3.14t)+sin(9.17t)+sin(12.57t)]

(7)

多频验证信号激励下的辨识模型与实际结构输出结果对比如图7(b)所示。为了定量比对辨识模型与实际结构的近似程度，定义模型吻合度指标

(8)

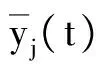
显然模型吻合度指标越接近100%，代表辨识模型与实际结构越接近，吻合度越高。表2给出了在扫频和验证两种实验情况下模型吻合度指标的计算值。图5、图7以及表3结果均表明：采用零点重新分布的传递函数模型G(s)的计算结果与实际结构响应基本一致，具有很高的吻合度。故可以用此模型代表实际结构进行后续的控制算法设计。

(a) 验证输入电压信号

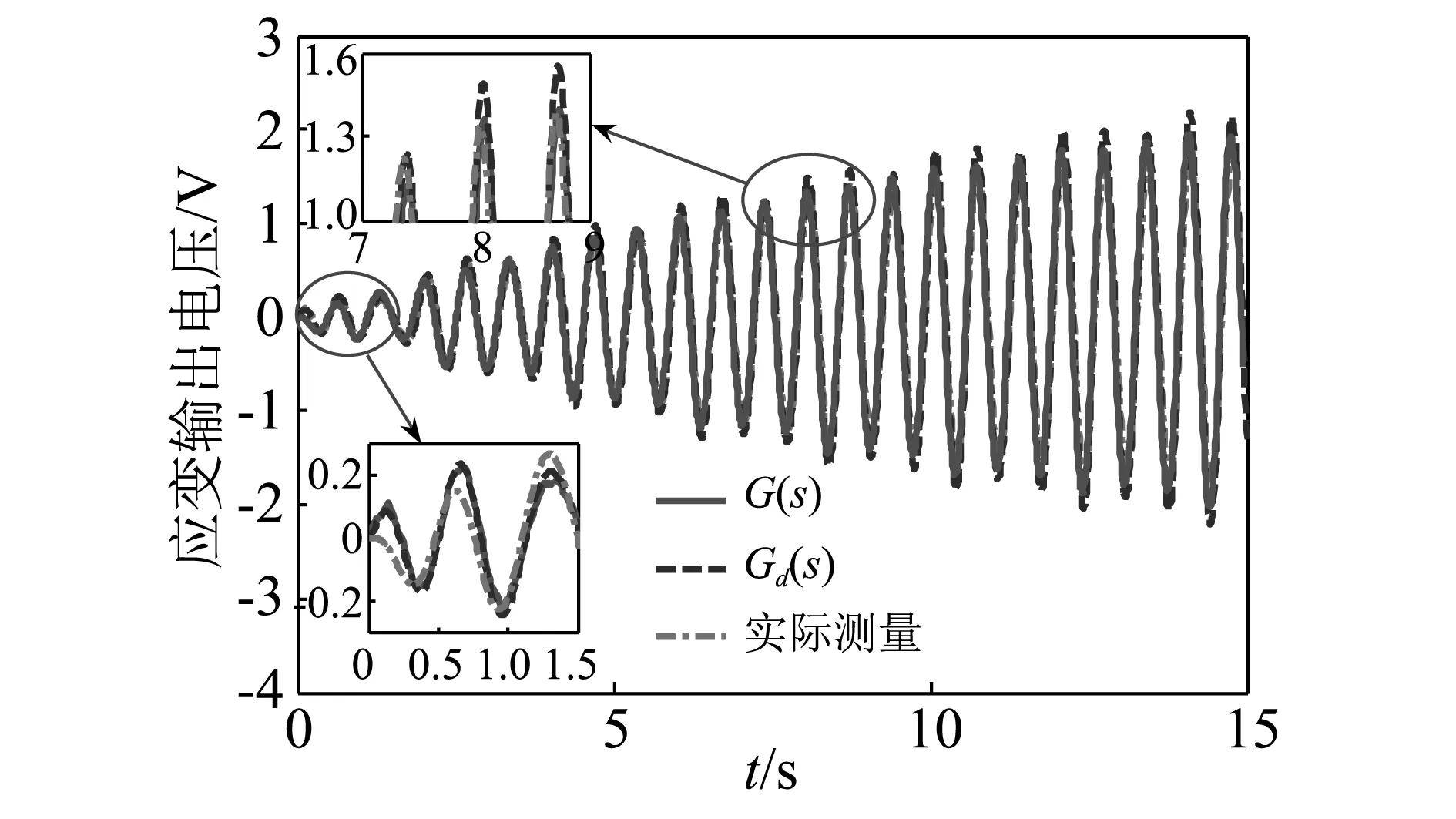
(b) 应变输出电压信号图7 验证信号下辨识模型与实验结果比较图Fig.7 Comparison of experimental results by the validation signal

辨识模型扫频实验验证实验G(s)94．85%88．95%Gd(s)89．45%81．68%

3 控制算法设计

柔性结构振动主动控制的本质是通过引入闭环控制增大结构的阻尼以减少结构在激励作用下的响应。极点配置法就是通过反馈增益矩阵改变原有受控结构系统的极点分布，从而使闭环系统的动态性能指标达到预期要求[17]。

为了利用极点配置法进行反馈增益设计，需先将系统模型转换为状态方程形式。定义加载在压电驱动器上的控制电压为系统输入u(t)，应变桥路的检测电压为系统输出y(t)，从能观的角度来构造系统状态方程为

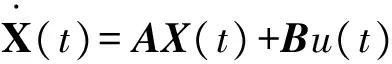
y(t)=CX(t)+Du(t)

(9)

式中：A,B,C及D分别为状态矩阵(向量)、输入矩阵(向量)、输出矩阵(向量)及转移矩阵(标量)；X(t)为状态变量(向量)。

如果反馈控制输入u(t)采用如下控制律

u(t)=-GX(t)

(10)

式中，G为反馈控制增益矩阵(向量)，其值由希望达到的闭环控制性能而定。

将式(10)中的控制输入u(t)带入状态方程式(9)得到

y(t)=CX(t)+Du(t)

(11)

该方程的解为

X(t)=e(A-BG)tX(0)

(12)

式中，X(0)为系统的初始状态。而系统的稳定性和响应特性都取决于矩阵A-BG的特征值。如果反馈控制增益矩阵G取值合理，那么矩阵A-BG就是渐近稳定的，因而矩阵A-BG的特征值也称为调节器零点，也就是系统的闭环极点。所谓的极点配置，就是要寻找适当的反馈控制增益矩阵G，使式(11)所示的闭环系统特征值，也就是闭环极点安排在指定位置上。

对于典型的二阶系统，系统的两个共轭极点一般可表示为

(13)

式中：ωn为二阶系统的固有频率，rad/s；ξ为结构阻尼比。

图8 复平面内的极点配置方法示意图Fig.8 Basic idea of the PA method in s-plane

从图6所示辨识模型的极点分布情况可以看到系统的共轭极点位于虚轴左侧，故系统是稳定的，但是由于二者距虚轴非常近，使得系统的开环阻尼效应非常弱，导致柔性臂的弹性振动要持续很长时间。为了缩短柔性臂振动的衰减时间，势必要将其极点左移，以增大系统闭环阻尼。考虑到压电致动器的驱动能力是有限的，存在着饱和电压，并适当抑制高频信号的干扰，设计系统的闭环阻尼比为0.5，采用图8所示的极点配置方法，根据式(13)确定的系统闭环极点见表3。为了对比不同闭环阻尼比下的控制效果，表中还给出了阻尼比分别为0.3和0.7时的闭环极点分布情况。

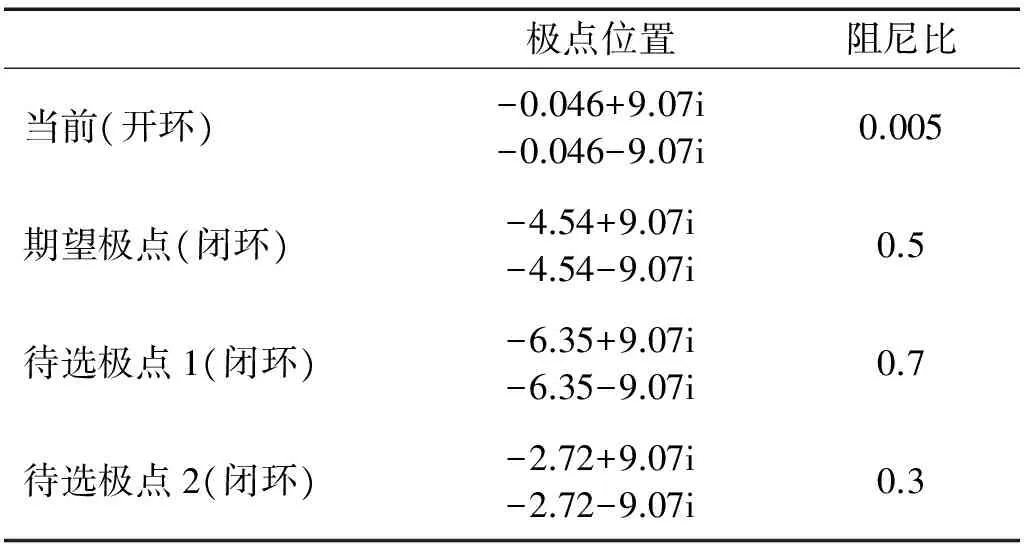
表3 系统极点配置表

在确定系统期望闭环极点的位置后，由于系统的闭环特征根就是系统的闭环极点，得到

(14)

根据式(14)即可求得系统反馈控制增益矩阵中的反馈控制系数。

4 控制效果验证

4.1 仿真验证

为验证提出的控制算法的有效性，基于得到的辨识模型G(s)开展仿真实验。仿真过程中首先对压电致动器施加激励信号激起柔性臂的振动，该激励信号由频率分别为1 Hz及1.5 Hz、幅值均为1 V的正弦信号叠加而成，激励时间为10 s。为了限制控制电压输出，仿真过程中还加入了一个限幅为±5 V的饱和模块。

图9给出了利用设计的控制器(闭环阻尼比0.5)对柔性臂的弹性振动进行抑制的仿真过程。从应变桥接电路输出电压的仿真变化过程可以看出：施加控制3 s后，柔性臂振动的振幅下降到0.1 V。与未施加控制的情况相比，PA控制器有效抑制了柔性臂的弹性振动，使柔性臂残余振动的衰减时间大大缩短。

基于表3中不同阻尼比下的闭环极点，图10给出了采用不同闭环极点下的仿真控制结果。与阻尼比取0.3时的极点位置相比，阻尼比0.5对应着距虚轴更远的闭环极点，故得到了更好的控制效果如图10(a)所示。但是当阻尼比取0.7时，由于闭环极点距离虚轴太远，受限于控制输入，闭环控制电压出现了饱和现象，见图10(b)中的黑色点画线。与阻尼比取0.5的情况相比，阻尼比取0.7时闭环控制效果并没有明显改善。所以阻尼比取0.5时的闭环极点位置是有限控制输入与闭环阻尼效应折中权衡下的最合适位置。

图9 施加控制时应变输出的仿真曲线Fig.9 Simulated responses of the sensor output with PA control

(a) 应变桥路输出电压

(b) 施加在致动器上的控制电压图10 不同配置极点下的仿真控制结果比较Fig.10 Comparison of simulated results with different locations of closed-loop poles

4.2 实验结果

同样采用仿真过程中的激励信号，图11给出了在10 s激励停止后，利用设计的控制器(闭环阻尼比0.5)对柔性臂的弹性振动进行抑制的实验过程。从应变桥接电路输出电压的实测曲线可以看出：施加控制5 s后，柔性臂振动的振幅下降到0.1 V；而如果不施加控制，其弹性振动经过20 s的自由衰减后振幅仍有0.4 V。不过对比仿真过程图9与实验结果图11可以看出：二者变化趋势基本相同，但是由于测试过程中噪声的干扰，削弱了压电致动器的抑振效果，实验中柔性臂的振动衰减时间稍微长于仿真结果。

图11 施加控制时应变输出电压的实验结果Fig.11 Experimental results of sensor output with PA control

从激光位移传感器采集到的柔性臂末端振动位移图12中可以看出：柔性臂结构自由衰减20 s后，其末端振动位移仍超过2 mm；而基于设计的控制器，柔性臂末端的振动位移在施加控制9 s后已衰减到0.1 mm，可认为其振动已经停止。显然柔性臂的振动得到了有效抑制，振动持续时间显著缩短。

图12 施加控制时柔性臂末端的振动位移Fig.12 Tip displacement of the manipulator with PA control

图13进一步给出了采用不同闭环极点下的实际控制效果。可以看出不同闭环极点位置下的实验控制效果与仿真结果基本一致。当阻尼比取值较小时(ξ=0.3)，控制器的控制效果较弱，柔性臂振动的衰减时间较长。而当阻尼比取值过大时(ξ=0.7)，由于致动器控制电压有限，导致控制器的计算输出超过了致动器的控制电压限制，出现了控制饱和现象。其控制效果并没有明显改善。实验结果进一步验证了阻尼比取0.5是最合适的。

为了进一步验证所提出的极点配置控制方法的有效性，利用电磁激振器的激励作为外扰激起柔性臂的弹性振动，柔性臂在控制器作用下的振动响应如图14所示。显然外界干扰激起了柔性臂强烈的弹性振动，其末端初始振幅达5 mm左右，如果仅靠柔性臂结构自身的阻尼衰减，其末端振动在自由衰减50 s才能停止。而在加入压电致动器的主动控制作用后，柔性臂振动的衰减速度明显加快，振动衰减时间缩短为16 s。故所提出的基于极点配置法的抑振控制策略是有效的，提高了柔性臂末端的定位精度和操作效率。

(a) 应变桥路输出电压

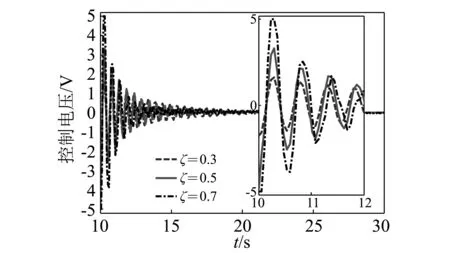
(b) 压电致动器的控制电压曲线图13 不同配置极点下的实际控制效果比较Fig.13 Comparison of experimental results with different locations of closed-loop poles

(a) 应变桥路输出电压

(b) 柔性臂的末端振动位移图14 外界干扰下柔性臂振动的实验结果Fig.14 Experimental results of vibration response of the manipulator with external disturbance

5 结论

研究了压电柔性臂系统的实验辨识问题，提出了零点重新分布的降阶传递函数模型。实验结果表明辨识得到的系统模型更好地补偿了模态截断效应，与实际系统输出具有较高的吻合度，提高了压电柔性臂系统的建模精度。为了抑制压电柔性臂的弹性振动，提出了一种移动距离最短、满足系统闭环阻尼要求的最优极点配置方法。仿真和实验结果证明了所提出的控制方法的有效性，缩短了柔性臂的振动衰减时间。本文提出的方法可为智能柔性结构模型建立和振动主动控制策略设计提供参考。

[ 1 ] 娄军强,魏燕定,杨依领, 等. 智能柔性构件振动改进多模态正位置反馈控制[J]. 振动与冲击, 2015, 34(10): 115-120. LOU Junqiang, WEI Yanding, YANG Yiling, et al. Modified multi-mode positive position feedback controller for active vibration control of a smart flexible structure[J]. Journal of Vibration and Shock, 2015, 34(10): 115-120.

[ 2 ] 李生权, 季宏丽, 裘进浩, 等. 基于加速度反馈和自抗扰的加筋壁板结构复合振动控制[J]. 振动工程学报, 2012, 25(5): 532-539. LI Shengquan, JI Hongli, QIU Jinhao, et al. Composite vibration control for a stiffened panel structure using acceleration feedback and active disturbance rejection[J]. Journal of Vibration Engineering, 2012, 25(5): 532-539.

[ 3 ] 邱志成,许燕飞. 基于自适应RBF模糊神经网络的旋转柔性铰接梁的振动控制[J]. 振动与冲击, 2016, 35(7): 89-95. QIU Zhicheng, XU Yanfei. Vibration control of a rotating two-connected flexible beam using RBF-based self-adaptivefuzzy neural network[J]. Journal of Vibration and Shock, 2016, 35(7): 89-95.

[ 4 ] RAHIMI H N, NAZEMIZADEH M. Dynamic analysis and intelligent control techniques for flexible manipulators: a review[J]. Advanced Robotics, 2014, 28(2): 63-76.

[ 5 ] 王斌, 邱志成, 张宪民, 等. 气动驱动柔性臂自适应模糊振动控制[J]. 机械工程学报, 2013, 49(11): 50-60. WANG Bin, QIU Zhicheng, ZHANG Xianmin, et al. Adaptive fuzzy vibration control for flexible manipulator based on pneumatic driving[J]. Chinese Journal of Mechanical Engineering, 2013, 49(11): 50-60.

[ 6 ] KIANG C T, SPOWAGE A, YOONG C K. Review of control and sensor system of flexible manipulator[J]. Journal of Intelligent and Robotic Systems, 2014, 77(1): 187-213.

[ 7 ] SETHI V, FRANCHEK M A, SONG G. Active multimodal vibration suppression of a flexible structure with piezoceramic sensor and actuator by using loop shaping[J]. Journal of Vibration and Control, 2011, 17(13): 1994-2006.

[ 8 ] DRIELS M. 线性控制系统工程[M]. 金爱娟，李少龙，李航天，译. 北京：清华大学出版社, 2005.

[ 9 ] SETHI V, SONG G. Pole-placement vibration control of a flexible composite I-beam using piezoceramic sensors and actuators[J]. Journal of Thermoplastic Composite Materials, 2006, 19(3): 293-307.

[10] SETHI V, SONG G. Multimodal vibration control of a flexible structure using piezoceramic sensor and actuator[J]. Journal of Intelligent Material Systems and Structures, 2008, 19(5): 573-582.

[11] RAHMAN T, DARUS I Z M. Active vibration control using pole placement method of a flexible plate structure optimised by genetic algorithm[C]∥ IEEE Conference on Control, Systems and Industrial Informatics.[S.l.]: IEEE, 2012: 92-97.

[12] KUO T C, HUANG Y J, CHEN C Y, et al. Robust pole placement in a specified trapezoid region for flexible manipulators[J]. Journal of Optimization Theory and Applications, 2013, 159(2): 507-517.

[13] PREUMONT A. Vibration control of active structures: an introduction [M]. 3rd ed. Berlin: Springer, 2011.

[14] NOBAHARI H, KORDKHEILI S A H, AFSHARI S S. Hardware-in-the-loop optimization of an active vibration controller in a flexible beam structure using evolutionary algorithms[J]. Journal of Intelligent Material Systems and Structures, 2014, 25(10): 1211-1223.

[15] BU Xiongzhu, YE Lin, SU Zhongqing, et al. Active control of a flexible smart beam using a system identification technique based on ARMAX[J]. Smart Materials and Structures, 2003, 12(5): 845-850.

[16] ORSZULIK R R, SHAN J. Experimental study on active vibration control using genetic algorithm-based system identification and optimized positive position feedback[J]. Smart Materials and Structures, 2012, 21(12): 125014.

[17] 庞中华, 崔红. 系统辨识与自适应控制MATLAB仿真[M]. 北京: 北京航空航天大学出版社, 2012.

Experimental identification and vibration suppression of a piezoelectricflexible manipulator using an optimal poles-assignment method

LOU Junqiang1, LIAO Jiangjiang1, LI Guoping1, YANG Yiling2, WEI Yanding2

(1. Zhejiang Provincial Key Lab of Part Rolling Technology, College of Mechanical Engineering and Mechanics, Ningbo University, Ningbo 315211, China; 2. China Key Laboratory of Advanced Manufacturing Technology of Zhejiang Province, School of Mechanical Engineering,Zhejiang University, Hangzhou 310027, China)

Experimental identification and active vibration suppression of a piezoelectric flexible manipulator system using poles-assignment control were presented in this paper. A transfer function model with relocated zeros was developed for the flexible manipulator bonded with strain sensors and a piezoelectric actuator. A mathematical model between the input voltage of the piezoelectric actuator and the output voltage of the strain sensors was established through sweep excitation. The fitness could achieve up to 94.8%. Furthermore, the close coincidence between the identified model and the experimental system was verified through a multi-frequency signal excitation. Then, the state equations of the flexible manipulator system were derived. A poles-assignment method with the characteristics of the shortest displacement distance and desired close-loop damping ratio was proposed. The effectiveness of the proposed control method was validated by simulation and experiments with different locations of closed-loop poles. Experimental results show that elastic vibrations of the link caused by the sweep and external disturbance excitation are effectively suppressed using the poles-assignment controller. Consequently, the proposed method of experimental identification and poles assignment control is feasible and effective.

piezoelectric flexible manipulator; system identification; optimal poles assignment; active vibration control

国家自然科学基金(51505238&51375433); 浙江省自然科学基金(LQ15E050002);宁波市自然科学基金(2015A610145); 浙江省公益项目(2013C31017)

2016-04-26 修改稿收到日期： 2016-06-22

娄军强男，博士，讲师，1986年7月生

魏燕定男，博士，教授，1970年7月生

TH212；TH213.3

10.13465/j.cnki.jvs.2017.16.003