芯子间距对激光选区熔化成形AlSi10Mg点阵夹芯板弯曲性能的影响

2022-08-04王国伟杨家林吴鸿飞沈显峰田大庆

航空材料学报 2022年4期

张博,王国伟,杨家林,吴鸿飞,沈显峰*,田大庆*

（1.四川大学机械工程学院,成都 610065；2.中国工程物理研究院机械制造工艺研究所,四川绵阳 621900）

金属点阵材料兼具结构和功能双重特性，包括优良的吸声能力[1]、高导热性[2]、力学性能[3]、抗爆炸[4-5]、抗冲击[6]、隔热[7]性能等，且具有极高的可设计性，因此备受业界青睐。激光选区熔化（selective laser melting,SLM）技术是一种采用激光作为能量源，对金属粉末进行逐层扫描，将堆积的粉末床熔融来完成增材制造的技术。SLM 成形零件尺寸精度高、表面质量好、具有近乎100%的致密度且能够自由设计[8]，适合用于制造点阵夹芯结构。

已有很多研究者对点阵夹芯结构的弯曲性能开展了研究。Gibson等[9]以简单梁为基础，提出了点阵夹芯板在三点弯曲和四点弯曲时的挠度和载荷关系公式，表明在弯曲条件下面板主要承受弯曲载荷，点阵结构主要承受剪切载荷。Su等[10]通过在夹芯板面板上打孔以降低面板的弯曲强度，研究发现，当芯子的剪切强度和面板的弯曲强度相等时，夹芯板整体的弯曲强度最高。Li等[11]发现点阵夹芯板的失效模式会相互影响，比如面板皱曲会加剧芯子的剪切破坏。Liu等[12]研究发现相对于体心立方点阵结构，点阵夹芯板可以提供更优异的弯曲刚度、强度和能量吸收性能。可以看出，近年来的研究重点偏向于点阵夹芯板的强度和失效模式，而随着应用的不断扩展，某些工业领域开始关注轻质高刚度夹芯板，并对其性能调控提出了需求，但是关于结构参数对夹芯板的柱面弯曲刚度和载荷-挠度曲线的影响方面研究较少。

本工作主要研究结构参数对激光选区熔化成形的AlSi10Mg 高刚度点阵夹芯板弯曲性能的影响。为此设计两种类型的正方形点阵夹芯板，并采用有限元分析、理论推导来研究芯子间距和芯子排列方向对点阵夹芯板的柱面弯曲刚度、应力集中区域以及屈服和稳定塑性变形阶段初始载荷的影响规律，根据激光选区熔化技术成形的点阵夹芯板三点弯曲实验结果，对仿真结果进行验证。

1 实验材料与方法

1.1 点阵夹芯板结构

实验所用两种点阵夹芯板均为正方形点阵夹芯板，图1（a）为0°正方形点阵夹芯板模型，即芯子沿着x和y 方向等间距均匀分布，且芯子排列方向与x 轴方向夹角为0°，图1（b）所示为45°正方形点阵夹芯板模型，即芯子排列方向与x 轴方向夹角为45°。

图1 正方形点阵夹芯板结构示意图（a）0°正方形点阵；（b）45°正方形点阵Fig.1 Structural diagram of square lattice sandwich panel （a）square lattice of 0°；（b）square lattice of 45°

其中，芯子长径比n 可表示为：

式中：Hc为芯子高度；d 为芯子直径。

式中：ρ为表观密度；V 为外轮廓体积；ρs为基体材料密度；Vs为实体体积。可得到点阵夹芯板的质量m和相对密度的关联公式：

本实验两种点阵夹芯板的芯子均为圆柱状，直径d=1.8 mm，高度Hc=4.4 mm，长径比n=2.44，上下面板厚度tf=1.8 mm，两侧面板厚度tcf=1.8 mm，夹芯板总长度L=200 mm，总宽度B=50 mm，总厚度H=8 mm。

1.2 点阵夹芯板的制备和测试

所用材料为中航迈特公司生产的AlSi10Mg 气雾化粉末，主要成分为：Al 89.34%（质量分数，下同）、Si 10.11%、Mg 0.35%、Mn 0.2%。粉末粒径为20～60 μm。用于成形样品的SLM 设备为EOS M290 3D 打印机，成形工艺参数为：激光功率370 W、扫描速度1300 mm/s、扫描间距0.19 mm、层厚30 μm。样品于铝基板上成形，打印完成后，用电火花线切割将样品和基板分离，然后通过超声振动方法去除样品内部及表面附着的粉末。

按照ASTM C393/C393M—2020 实验标准，三点弯曲实验的支撑跨距l=140 mm，活动压头与固定支辊的端部均为圆柱形，直径D=20 mm，压头的加载速率设定为2 mm/min。设定挠度加载到8 mm 时停止加载。

1.3 有限元模拟方法

仿真实验主要探索芯子间距对点阵夹芯板弯曲性能的影响规律以及对比两种芯子排列方向之间的差异，因此对两种点阵夹芯板各自设计了5 组不同芯子间距的点阵夹芯板有限元模型，芯子间距及相应的点阵结构相对密度见表1。

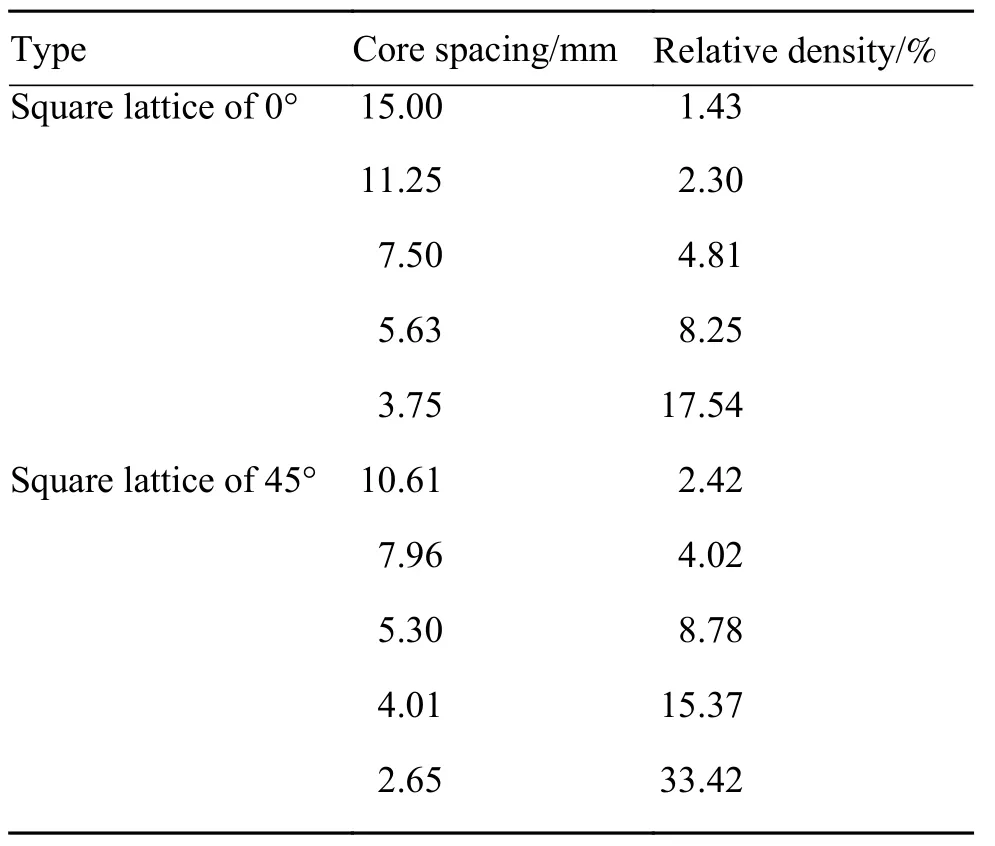
表1 点阵夹芯板有限元模型的芯子间距及相对密度Table 1 Core spacing and relative density of FEA lattice sandwich panel model

材料属性：在与夹芯板样品相同的工艺条件下，制备标准AlSi10Mg 拉伸试件进行拉伸实验，根据该拉伸曲线进行仿真材料参数的设置，其中弹性模量设为E=60 GPa、屈服强度 σy=201 MPa、抗拉强度Rm=313 MPa、泊松比为0.33。

边界条件：圆柱压头只能进行z 向运动，两支辊全约束。分别用CONTA174 单元和TARGE170单元来定义接触面和目标面，选择夹芯板上下表面为目标面，压头及两支辊圆弧面为接触面。接触刚度设为0.04～0.08，罚函数刚度0.5。仿真模型如图2所示。

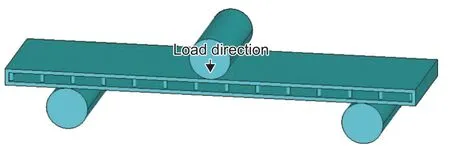
图2 有限元仿真模型Fig.2 FEA model

网格划分：采用SOLID95 单元对模型进行网格划分，有限元模型的网格划分节点数和单元数如表2所示。

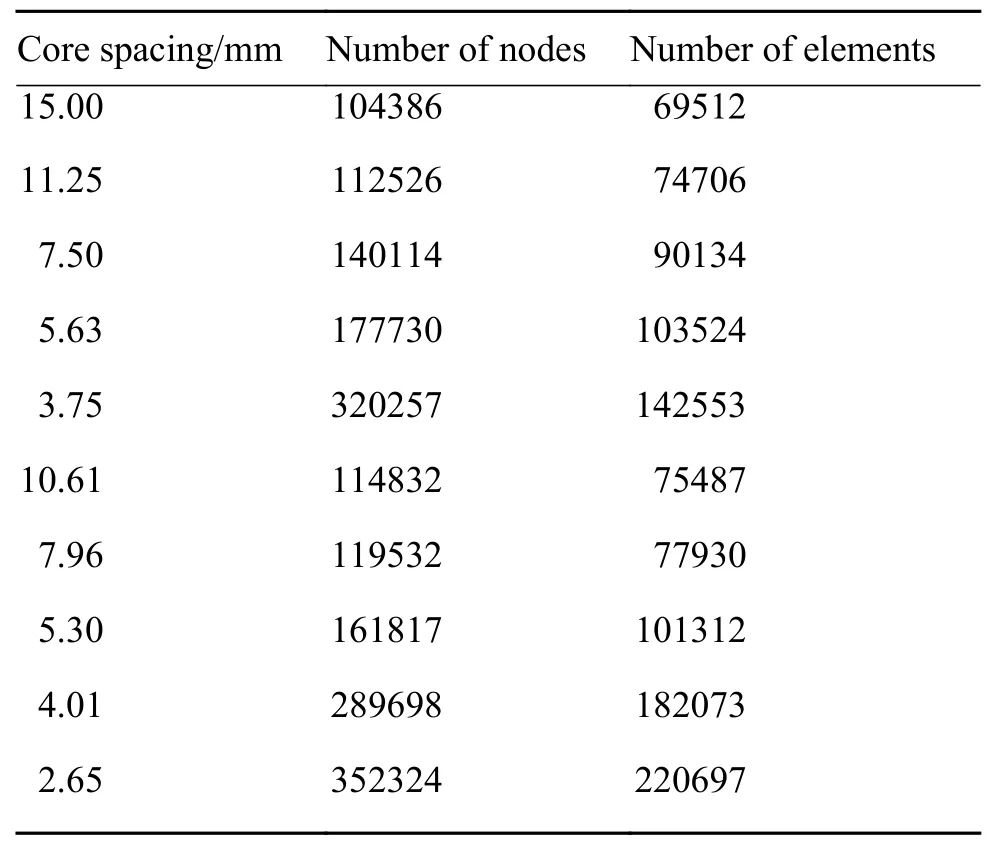
表2 有限元模型网格划分的节点数和单元数Table 2 Number of nodes and elements in mesh division of FEA model

2 结果及讨论

2.1 实验分析

图3（a）为样品的三点弯曲载荷-挠度曲线，弯曲最大挠度均为8 mm，其中芯子间距为3.75 mm、7.5 mm和15 mm的三组是0°点阵夹芯板样品，可以看出三组样品的弹性变形段斜率为1.46 kN/mm、1.01 kN/mm、0.46 kN/mm，7.5 mm和15 mm的失效载荷为2.69 kN、1.08 kN，3.75 mm 在最大挠度8 mm 时的载荷为5.37 kN，未发生失效。芯子间距为5.3 mm和10.61 mm的两组样品为45°点阵夹芯板，其弹性变形段斜率分别为1.24 kN/mm、0.63 kN/mm，失效载荷为4.32 kN、1.59 kN。

图3（b）、（c）为失效点阵夹芯板的局部变形图。由图3 可以看出，样品的失效模式为点阵结构中的芯子剪切破坏。从图3（a）中可以看出，除了芯子间距为3.75 mm的夹芯板外，其余夹芯板在达到失效载荷后，随着挠度增加，载荷发生下降，而当挠度继续增加，载荷由于夹芯板的剩余承载性能[12]不再锐减。点阵夹芯板的失效载荷主要取决于面板和点阵结构的承载性能，当芯子断裂后剩余承载性能主要取决于面板的承载性能，随着芯子间距的降低，点阵结构的承载性能增强，夹芯板失效载荷和剩余承载性能差距也随之增大，造成了点阵结构失效后载荷的下降幅度越来越大，以至于如曲线45°-5.3 mm的大幅骤降。

图3 点阵夹芯板三点弯曲实验（a）载荷-挠度曲线；（b）芯子间距15 mm的0°点阵夹芯板局部变形图；（c）芯子间距5.3 mm的45°点阵夹芯板局部变形图Fig.3 Lattice sandwich panel after three-point bending （a）load-deflection curves；（b）local deformation diagram of 15 mm lattice sandwich panel of 0°；（c）local deformation diagram of 5.3 mm lattice sandwich panel of 45°

综上可知，对于0°和45°两种类型的点阵夹芯板，随着芯子间距的减小，点阵夹芯板的弹性变形段斜率和失效载荷均明显提高，夹芯板发生失效的挠度值增大，说明减小芯子间距可以明显提高夹芯板的弯曲性能。

2.2 有限元分析

分析5 组芯子间距分别为15 mm、11.25 mm、7.5 mm、5.63 mm和3.75 mm的0°点阵夹芯板，以及芯子间距为10.61 mm、7.96 mm、5.3 mm、4.01 mm和2.65 mm的45°点阵夹芯板，仿真得到的载荷-挠度曲线弹性变形段斜率，见表3。

表3 不同芯子间距点阵夹芯板载荷-挠度曲弹性变形段斜率Table 3 Linear slope of load-deflection curve of sandwich panels with different core spacings

2.2.1 点阵夹芯板的柱面弯曲刚度

根据Gibson[9]夹芯板理论，三点弯曲载荷-挠度曲线弹性变形段的斜率公式为：

式中：P 为载荷；δ 为挠度；Deq和 (AG)eq分别为夹芯板的面板等效弯曲刚度和点阵结构等效剪切刚度。可以认为载荷-挠度曲线弹性变形段斜率为夹芯板的柱面弯曲刚度[13]。

图4（a）、（b）为仿真结果的柱面弯曲刚度与芯子间距的拟合曲线。图4（c）为仿真柱面弯曲刚度与相对密度的拟合曲线。

从图4（a）、（b）可以看出，0°和45°点阵夹芯板的柱面弯曲刚度随着芯子间距的增加而减小，拟合结果表明，在芯子间距为2.65～15 mm的范围内，柱面弯曲刚度和芯子间距之间有明显的线性关系（0°和45°点阵夹芯板拟合的决定系数 R2分别为0.97213和0.98276）。同时通过对比拟合公式，发现45°点阵夹芯板拟合曲线的斜率绝对值大于0°点阵夹芯板，认为芯子间距对45°点阵夹芯板柱面弯曲刚度的影响更加显著。从图4（c）中可以看出，对于0°和45°点阵夹芯板，相对密度与柱面弯曲刚度拟合的决定系数分别为0.9929和0.9845，而两条曲线基本重合，这说明两种点阵夹芯板在相同相对密度下的柱面弯曲刚度基本一致，结合式（3）可以看出在相同质量下柱面弯曲刚度也基本一致。同时可以看出，当相对密度小于5%时，相对密度对柱面弯曲刚度有显著影响，而当相对密度大于5%后影响逐渐降低。

图4 点阵夹芯板的柱面弯曲刚度（a）0°点阵夹芯板芯子间距与柱面弯曲刚度的拟合曲线；（b）45°点阵夹芯板芯子间距与柱面弯曲刚度拟合曲线；（c）相对密度与柱面弯曲刚度拟合曲线Fig.4 Cylindrical bending stiffness of lattice sandwich panels （a）fitting curve of core spacing and cylindrical bending stiffness of 0°；（b）fitting curve of core spacing and cylindrical bending stiffness of 45°；（c）fitting curve of relative density and cylindrical bending stiffness

2.2.2 变形失效分析

图5 为芯子间距分别为2.65 mm、4.01 mm、5.3 mm、7.96 mm和10.61 mm的45°点阵夹芯板在失效载荷（或最大载荷）下的Von-Mises 应力云图。由图5 可以看出，芯子间距为2.65 mm和4.01 mm的点阵夹芯板，与压头接触的面板位置处有明显的应力集中，芯子间距为7.96 mm和10.61 mm的夹芯板，应力集中区域主要在芯子与面板的连接处，而芯子间距为5.3 mm的夹芯板，其应力分布较为均匀。

图5 45°点阵夹芯板Von-Mises 应力云图Fig.5 Von-Mises stress on lattice sandwich panels of 45°

可以认为，点阵夹芯板在三点弯曲后的应力集中区域会随着芯子间距的改变而改变。当芯子间距较小时，应力集中位置在与压头接触的面板处，可以认为该处首先发生塑性变形和破坏，而随着芯子间距增大，应力集中位置向芯子两端转移。分析该现象的原因主要是，当芯子间距较小时，点阵结构相对密度较大，点阵结构整体强度和抗剪刚度高[14]，其抗弯承载性能高于面板，因此在面板处有较大变形，存在应力集中现象。随着芯子间距的增大，点阵结构的强度和抗剪刚度减小，其抗弯承载性能减小，从而发生较大变形[15]，根据圣维南原理，在芯子的两端产生较大应力集中。

对于点阵夹芯板柱面弯曲，顶部面板会在塑性变形中扩大与压头的接触面积，从而促进弯曲载荷从中心处的芯子向周围芯子传递，本研究所用面板相对较厚，使得这种“应力传递”[12]现象更为明显，所以应力和载荷在芯子间分布较为均匀。

2.3 理论预测

根据图3（a）点阵夹芯板载荷-挠度曲线可以得到，夹芯板在三点弯曲变形过程中主要有四个阶段：弹性变形阶段、屈服阶段、稳定塑性变形阶段和失效阶段。根据图5 可知，当芯子间距较小时，夹芯板中与压头接触的面板区域首先发生塑性变形。点阵夹芯板在三点弯曲下的受力情况如图6所示。

夹芯板承载达到屈服阶段初始载荷时的中心横截面应力分布如图6（c）所示，根据应力云图，通过近似处理得到σs=210.5 MPa，从而可得此时夹芯板中心横截面处的弯矩My：

图6 夹芯板三点弯曲时实验（a）x 轴方向弯矩图；（b）x 轴方向剪力图；（c）承载达到屈服阶段初始载荷时中心横截面应力示意图；（d）承载达到稳定塑性变形阶段初始载荷时中心横截面应力示意图Fig.6 Sandwich panel under three-point bending （a）cylindrical bending moment diagram in the x-axis direction；（b）shear load diagram in the x-axis direction；（c）schematic diagram of stress at central cross section under initial load at yield stage；（d）schematic diagram of stress at central cross section under initial load at plastic stage

式中：c 为横截面处芯子个数；d 为芯子直径；Hc为芯子高度；B 为夹芯板总宽度；H 为夹芯板总厚度；tf为面板厚度。

中心横截面处的弯矩Mmax也可表示为：

式中：P 为载荷；l 为支撑跨距。

由式（5）、（6）可得屈服阶段初始载荷 Py的预测公式为：

随着挠度的进一步增加，夹芯板进入稳定塑性变形阶段，根据应力云图，通过近似处理得到此时σs=235 MPa，夹芯板承载达到稳定塑性变形阶段初始载荷时的中心横截面应力分布如图6（d）所示，夹芯板中心横截面处的弯矩可表示为：

结合式（6）可得稳定塑性变形阶段初始载荷Pp的预测公式为：

根据式（7）、（9）可得不同芯子间距点阵夹芯板的 Py和 Pp的理论值，该理论值与仿真值对比见表4。可以看出，最大相对误差小于7.6%。

表4 Py和Pp的理论值和仿真值对比Table 4 Comparison of theoretical and FEA values of Py and Pp

根据图5 可知，当芯子间距较大时，芯子首先发生塑性变形，夹芯板在屈服阶段初始载荷下，压头和支辊间芯子上的应力大小和分布状态几乎一致，在稳定塑性变形阶段初始载荷下也有同样现象，由于芯子主要承受剪切载荷，可以认为剪切载荷均匀地分布在这些芯子上,因此左右支辊到压头范围内的每根芯子所受的剪切载荷 Plc和 Prc可表示为：

式中：a 为左右支辊之间的芯子数；P 为载荷。a 与点阵结构相对密度之间有如下关系：

可得到载荷P 预测公式为

式中：B 为夹芯板总宽度；l 为支撑跨距；d 为芯子直径。根据芯子间距为15 mm的0°点阵夹芯板的实验数据，分别可得屈服阶段和稳定塑性变形阶段初始时分别有Plc=0.012 kN，Plc=0.016 kN，由此可得屈服和稳定塑性变形阶段初始载荷 Py和 Pp的预测公式为

根据式（14）、（15）可得不同芯子间距点阵夹芯板 Py和 Pp的理论值，该理论值与仿真值对比见表5。可以看出，最大相对误差小于13.6%。

表5 Py和Pp的理论值与仿真值对比Table 5 Comparison of theoretical and FEA values of Py and Pp

2.4 仿真与实验结果对比分析

图7所示为点阵夹芯板实验和仿真结果对比。由图7 可以看出，在弹性变形阶段两者结果基本一致，柱面弯曲刚度对比见表6，两者相对误差小于6.5%；但在屈服阶段和稳定塑性变形阶段，仿真结果较实验结果的载荷较小。仿真和实验的误差来自样品的成形质量[16]，可能是由于本研究的激光功率较大导致熔池宽度较大，从而使得芯子的杆径较模型更大。但整体而言，仿真与实验吻合度较高。

表6 正方形点阵夹芯板柱面弯曲刚度的实验值与仿真值对比Table 6 Comparison of experimental and FEA cylindrical bending stiffness values of square lattice sandwich panel

图7 实验和仿真载荷-挠度曲线对比（a）0°点阵夹芯板；（b）45°点阵夹芯板Fig.7 Comparison of experimental and FEA load-deflection curves （a）square lattice of 0°；（b）square lattice of 45°

图8 为实验变形和仿真应力云图对比。从图8（a）可以看出，芯子间距为3.75 mm的0°点阵夹芯板的面板在压头附近的局部变形明显，认为该处首先发生塑性变形和破坏，与图8（b）实验变形一致，同时可以看出支辊附近的面板没有局部变形。从图8（c）可以看出，芯子间距为7.5 mm的0°点阵夹芯板的面板在支辊附近的局部变形明显，同时在该处应力云图中有较大的局部应力，可以认为该处首先发生塑性变形，与图8（d）中的变形吻合。考虑产生上述现象的原因是，当芯子间距较小时，在支辊附近的局部刚度较大，局部变形较小，随着芯子间距的增大，其局部刚度降低，所以局部变形逐渐增大。

图8 实验与仿真结果对比（a）3.75 mm 芯子间距点阵夹芯板应力云图；（b）3.75 mm 芯子间距点阵夹芯板变形；（c）7.5 mm芯子间距点阵夹芯板应力云图；（d）7.5 mm 芯子间距点阵夹芯板变形Fig.8 Comparison of experimental and FEA results （a）Von-Mises stress of lattice sandwich panel of 3.75 mm；（b）deformation of lattice sandwich panel of 3.75 mm；（c）Von-Mises stress of lattice sandwich panel of 7.5 mm；（d）deformation of lattice sandwich panel of 7.5 mm

芯子间距为3.75 mm的0°点阵夹芯板只有压头下发生一处局部变形，上下面板的变形差别不大，因此芯子仍然保持相对面板垂直的状态，如图8（a）、（b）所示。芯子间距为7.5 mm的0°点阵夹芯板的面板在压头和支辊附近发生三处局部变形，上下面板沿长度方向的变形差别较大，造成芯子相对于面板倾斜，如图8（c）、（d）所示。结果表明，通过仿真可以有效地预测夹芯板的变形和失效模式，仿真结果准确可靠。