厘清概念与性质 准确把握解题方向

广东 林国红

根据《普通高中数学课程标准(2017年版)》的内容可知：数学教育应帮助学生掌握现代生活和进一步学习所必需的数学基础知识、基本技能、基本思想、基本活动经验.通过学习，经历数学知识的发生、发展，体验研究数学的方法，感悟数学的科学价值、应用价值、文化价值和审美价值，促进学生思维能力、实践能力和创新意识的发展，培养一定的解题技能.其中，基础知识不外是定义、定理、公式、性质等，往往一个概念产生之后，随之便有若干性质.在解题过程中，如何理解概念，巧用性质，是一个值得思考的问题.很多学生不能很好地理解概念和性质，从而造成解题失误.

下面以奇函数为例，谈谈厘清概念与性质在解题中的重要性，供大家参考.

一、奇函数的定义及其性质

一般地，如果对于函数f(x)的定义域内任意一个x，都有f(-x)=-f(x)，那么函数f(x)就叫做奇函数.

基于奇函数的定义，可以得到以下性质：

1.奇函数的定义域关于原点(0,0)对称.

2.对于定义域内的一个x0，总有f(-x0)=-f(x0)成立，特别地，当f(0)有意义时，有f(0)=0，即函数f(x)过原点.

3.奇函数的图象关于原点(0,0)成中心对称，反之，函数图象关于原点(0,0)成中心对称的函数一定是奇函数.

二、奇函数中常见错误问题梳理

1.错用性质f(0)=0

错因分析如果函数的定义域是包含0的奇函数，则能得到f(0)=0，但满足f(0)=0的函数不一定是奇函数，而且根据函数f(x)的解析式，并不能肯定当x=0时，函数f(x)有意义.因此，本题利用f(0)=0来解答是不正确的.

所以1-a2=0，解得a=±1.

错解由f(x)为奇函数，得f(0)=0，即lga=0，所以a=1，

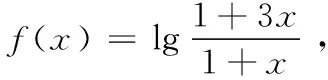
所以不存在实数a使函数f(x)是奇函数.

错因分析根据函数f(x)的解析式，我们无法确定函数f(x)在0处是否有定义，所以不能应用f(0)=0解题.

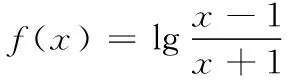
所以当a=-1时，函数f(x)是奇函数.

【例3】若函数f(x)=ax3+(a-1)x2+a(a-1)是奇函数，求实数a的值.

错解因为f(x)是奇函数，所以f(0)=a(a-1)=0，解得a=0或a=1.

错因分析当f(x)在0处有定义，且f(x)为奇函数时，则有f(0)=0，但f(0)=0并不能说明f(x)为奇函数，即当f(x)在0处有定义时，f(0)=0只是f(x)为奇函数的必要非充分条件，所以用f(0)=0求出a的值后必须进行检验，这种检验是解题过程中不可缺少的步骤.

正解因为f(x)是奇函数，所以f(0)=a(a-1)=0，解得a=0或a=1，

当a=0时，f(x)=-x2，f(x)不是奇函数，所以a≠0；

当a=1时，f(x)=x3，f(x)是奇函数，所以a=1.

评注当能确定函数在0处有定义时，f(0)=0只是f(x)为奇函数的必要非充分条件，用其求出参数的值后，还要验证这个值是否是函数为奇函数的充分条件；当不能确定函数在0处是否有定义时，f(0)=0是f(x)为奇函数的既不充分也不必要条件，这时只能用奇函数的定义或其他方法去求参数的值.

2.求函数解析式漏掉f(0)=0

【例4】已知定义在R上的奇函数f(x)，当x>0时，f(x)=-x2+2x.求函数f(x)的解析式.

错解当x<0时，-x>0，因此f(-x)=-(-x)2+2(-x)=-x2-2x，而f(x)为奇函数，故f(x)=-f(-x)=x2+2x，

错因分析这种错误是学生做题时最为常见的错误，容易忽略在奇函数中，f(x)在0处有定义时，则有f(0)=0.

正解当x<0时，-x>0，因此f(-x)=-(-x)2+2(-x)=-x2-2x，而f(x)为奇函数，故f(x)=-f(-x)=x2+2x.

又因为f(x)是R上的奇函数，从而f(0)=0.

3.忽视函数的定义域

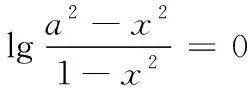
三、合理应用奇函数的定义与性质，精准快速解题

解由题意可知f(x)的定义域为{x|x≠0}，且f(x)是奇函数，故f(-1)+f(1)=0，又f(1)=0，从而f(-1)=0，所以a=1.

所以不等式f(x)<0的解集为{x|-11}.

四、结语

数学概念是构建数学理论大厦的基石，是推导数学定理、公式及性质的逻辑基础，而性质是概念的延伸，两者密不可分.在数学解题过程中，很多出错的原因是对概念与性质的理解不够透彻，又或者是思考不全面等，从而对概念与性质的转化应用不灵活.所以在平时的学习中，不能只强调解题的方法与技巧，而忽略基本概念与性质，要深刻理解概念与性质，以及两者的联系，才能找准解题的思路与方向，提高解题能力.

五、练习巩固

最后提供三道试题作为练习，以加深体会奇函数的定义与性质在解题中的应用.

1.若函数f(x) = ex+ae-x(x∈R)是奇函数，求实数a的值.