奏响探究音符 提高解题效益
2017-08-23天津市静海区沿庄镇中学刘家良邮编301605
天津市静海区沿庄镇中学 刘家良 (邮编:301605)
奏响探究音符 提高解题效益
天津市静海区沿庄镇中学 刘家良 (邮编:301605)
教者抛出问题时,不要急于将答案呈现给学生,而是要给足学生时间让学生去想,大胆去说、去议、去争,激励多样化探究,尊重差异性思维,辩证评析每类想法,为学生营造一种积极向上的进取氛围.
多种化;探究;尊重差异;辩证评析
教师布置完一道题后,要给学生足够的时间,以让学生静下心来去想,有了想法时再让学生尽情地去说,说的学生多了后再让他们“七嘴八舌”去议、去争、去评,而此时的教师应尽可能地为每名学生提供“演说”的机会,唤醒、激励学生多样化的探究,要尊重学生的差异性思维,在此基础上辩证析评他们中的每种解法,为学生营造一种积极向上的进取氛围.这样,既减少了教师唱“独角戏”的尴尬场面,又能使我们的习题教学能“乱中取胜”.
1 引例呈现
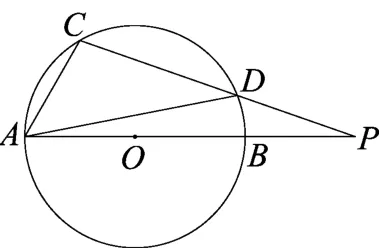
图1
例 如图1,AB是☉O的直径,AB和弦CD的延长线相交于点P.若∠CAP=60°,∠P=20°.求∠DAP的度数.
意图 2013年人教版教材中关于圆内接四边形性质相应的题中只有一个(88页第5题),因训练少,唯恐“水过地皮湿”,特安排此题让学生巩固圆内接四边形的对角互补性(这只是笔者的预设).
课堂展示:
师:上节课中我们学过圆周角及其性质、推论,并由圆周角的性质推导出圆内接四边形的性质.本节课检验同学们对上述知识的掌握情况.请大家思考.
生1:“见直径,想直角”.如图2,连接BC,则∠ACB=90°.因∠CAP=60°,所以∠ABC=30°.因为∠ADC与∠ABC均为弧AC所对的圆周角,所以∠ADC=∠ABC=30°.又∠ADC是△ADP的外角,所以∠DAP=∠ADC-∠P=30°-20°=10°.

图2
师:生1利用直径所对的圆周角为直角和同弧所对的圆周角相等的性质,并结合三角形的外角性质得到了所求角的度数,思路流畅、表述准确.
生2:(话音未落,迫不及待)连接BC,∠ABC=30°.∠ABC是△CBP的外角,得∠BCP=10°.又∠DAP与∠BCP同为弧BD所对的圆周角,故∠DAP=∠BCP=10°.
生3:生2和生1都利用了直径所对的圆周角为直角、同弧所对的圆周角相等及其三角形的外角性质,再者都是将所求角置身于三角形中,虽然视角不同,但转换上可为“异曲同工”.
师:生3将两名学生的解法进行比较,提炼共性,概括到位,值得同学们学习.
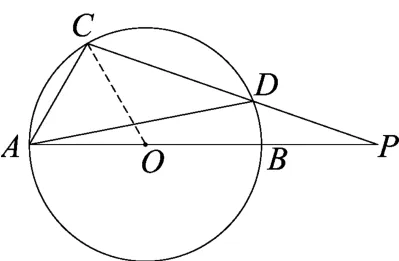
图3
生4:如图3,连接OC.因∠CAP=60°,OA=OC,所以△AOC为等边三角形,∠AOC=60°.又圆周角∠ADC和圆心角∠AOC所对的弧为弧AC,所以
之后就和生1的解法一样了.
师:生4由∠CAP=60°联想到等边三角形,并发现∠ADC和∠AOC之间的关系,得∠ADC的度数.生3和生1虽都求∠ADC的度数,但路径有别.同学们的思维越发活跃了!
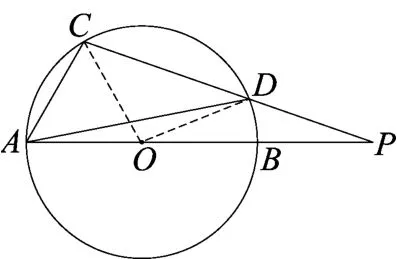
图4
生5:如图4,连接OC、OD,得∠OCD=40°.由OC=OD,得∠ODC=∠OCD=40°.因∠ODC是△ODP的外角,所以∠BOD=∠ODC-∠P= 20°.又圆周角∠DAP和圆心角∠BOD所对的弧均为弧BD,所以
生6:生5比生4的解法多了一条辅助线,环节多,这种方法拙了些!
生7:我不同意生6的看法,环节虽多了些,但从这种方法中发现了DP的长就是圆的半径,从这点上看,我应给生5点个赞!
师:追求解法的简捷毋容置疑,但只要是自己所想,无论解法是简是拙,都值得同学们去点赞.生6善于比对,比对是学习过程中不可或缺的习惯,值得学习,而生7懂得欣赏别人的长处,大家应追求这种“一分为二”看问题的思维品质.(拔高调)还有无其他解法?
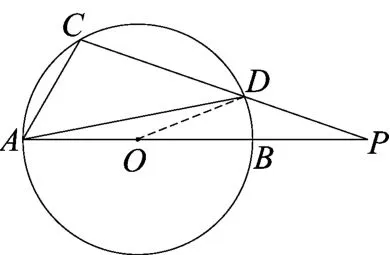
图5
生8:(急忙站起)如图5,连接OD.由于圆周角∠C(∠C=100°)和优角∠AOD所对的弧均为优弧ABD,故优角∠AOD=200°,从而∠BOD=20°.接下来和生5一样了.
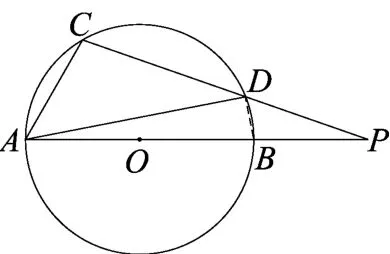
图6
师:同学们从三角形的外角、同一条弧所对的圆周角和圆心角的关系作切入,可为“八仙过海,各显神通”.还有不同的解法吗?生9:如图6,点A、B、D、C四点在☉O上,连接BD,可得圆内接四边形ABDC.根据圆内接四边形对角互补行,得∠BDC=180°-∠CAP=120°.因AB为☉O直径,所以∠ADB=90°,∠ADC= 30°.接下来和生1的解法一样了.
师:生9求∠ADC的度数,另辟蹊径,这种求新求异的精神值得大家学习.前后共有3个同学(生1,生4,生9)从不同角度求得∠ADC的度数.你们的答案是老师始料未及,让老师由衷佩服!
2 奏响探究多样之音,提高解题教学效益
本来设置此题是来巩固圆内接四边形的性质,但课堂生成“偏离”了预设的轨道,学生的多种解法令教师惊叹,不得不刮目相看了.解题教学作为课堂重要一环,而此案例恰好为提高解题教学的效益提供了一个思路启示.
2.1 学生探究,教师要舍得“等”
探个究竟是人生之俱来的本性,而解题离不开学生的自我探寻.问题是思维的方向和动力,当教者提出问题之后,不要急于让学生马上回答,需要耐心“等一等”,给学生足够的思考空间和时间,等出学生“愤”、“悱”后瞬间闪烁的智慧火花,等到“众里寻他千百度,蓦然回首,那人却在灯火阑珊处”的惊喜与冲动![1]不断地鼓励、启发,营造人人想说、要说、善说的课堂氛围,张扬学生个性,久之,个性化思维就得以绽放,多样化思维得以齐放.有些老师忙于赶进度,出现了“讲”替代“探”的现象,压得学生喘不过气来,知识被做成了“夹生饭”,学生吃不消,时间一长,兴趣也就索性全无了.所以衡量解题教学效益要以绝大部分学生的能力是否能跟得上,思维是否活跃、探究是否多样为试金石.
案例1 已知☉O的半径为r,圆心O到直线l的距离为d,且r、d是关于x的一元二次方程x2+2mx+1=0的两个根,若直线l和☉O相切,则m的值为____.
生1:当直线l和☉O相切时,有d=r,此时关于x的一元二次方程x2+2mx+1=0有两个相等的实数根,所以△=0,即4m2-4=0,得m=±1.
师:有不同的结果吗?
生2:m=-1.因为方程的两个根“身份”特殊,都为正数,由根与系数的关系,得r+d=-2m>0,故m<0,所以m=1应舍去.m=-1.
众生:鼓掌!
生3:设y=x2+2mx+1.由题意,知其图象应为抛物线的一部分,顶点落在x轴上,对称轴位于y轴右侧,即由此解得的结果与生2相同.
感情上的事,谁能说得清楚?风影开始看着红琴笑,他什么也不说,只是瞅着她笑,有点儿像佛拈花微笑。这种笑意味深长,是怜悯她?是鄙夷她?是睥睨她?是讥讽她?抑或是善意地劝导她,开悟她?
众生:再次鼓掌!
师:这名学生站在二次函数图象的层面去思考,数形结合思想用活了.
一个填空题,仅等了5分钟,学生就“补全”了答案,且后者的思维让同学们瞠目结舌.
2.2 鼓励和尊重并行
有多样就存在差异,鼓励学生多样化思维和尊重学生差异性思维两者之间是相辅相成的.所以教师设置问题时,应尽可能多视角性,如开放性试题、一题多解等.同时对一个问题,教师要根据学情从多方面做出预设,遇到这个问题时学生怎么想,存在哪些想法,这样,教师析评就会有的放矢、富有针对性,而对学生没有考虑到的解法,应予以引导或点拨.对学生的解答,要引导学生一分为二,辩证析评,不仅要有称赞,还要从“拙”的解法中寻找出其蕴藏的亮点.只要学生动脑想,哪怕“节外生枝”,都要给其中积极的因素和正确的东西以尊重,别伤害学生自尊.
案例2 如何寻找一个圆形纸片的圆心?
分析 随着“圆”知识的增厚,途径越发广泛.如将三角板的直角顶点放在圆周上,得到直径,再取其中点;在圆周上任取三点构造圆内接三角形,作两边的垂直平分线,交点即是圆心;在圆周上任取两点分别作圆的切线,过两切点分别作两条切线的垂线,交点即是圆心;将圆对折两次,折叠的交点即是圆心.
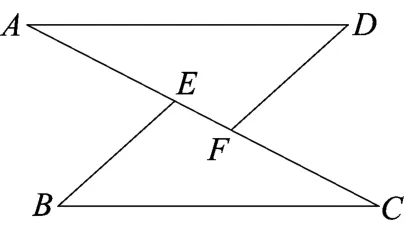
图7
案例3 如图7,在△BEC和△DFA中,点A、E、F、C在同一直线上,现有下面四个论断:
(1)AD=CB;(2)∠B=∠D;(3)AE=CF; (4)AD∥BC.
请你用其中的三个作为条件,余下的一个作为结论,编写一道数学问题,并写出解答过程.
分析 此题考查全等三角形的判定与性质,因判定法有四种,故此学生切入点就会有别.
生:若此题的四个论断能分别作为结论,则出现四种可能,分别是(1),(2),(3)→(4);(1), (2),(4)→(3);(1),(3),(4)→(2);(2),(3),(4)→(1).
师:这四种情况都成立吗?根据是什么?
在不断地追问声中,学生在分类中取舍合理,养成了严谨的思维.如有部分学生注意到“(1),(2),(3)→(4)”此种情况不成立.但应鼓励想到有这种可能情形的学生.
3 主线贯穿,适时留白
学生思维放开了,但教师作为课堂的组织者和引导者,要“放”中有“收”,要从多种方法中引导学生提炼、概括和归纳解这类题的通法、通则,并从不同的解法中寻找出共同之处.也就是问题解答中的主线,有时还要在某个地方适时“留白”,进一步激起学生的好奇心和求知欲.
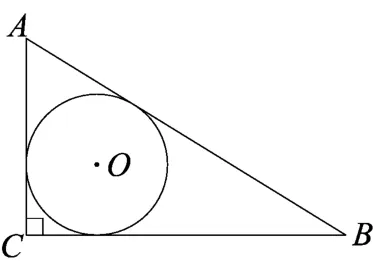
图8
案例4[2]如图8, Rt△ABC中,∠C=90°, AB、BC、CA的长分别为c、a、b,求△ABC的内切圆半径r.(2013年人教版九上103页习题24.2第15题)
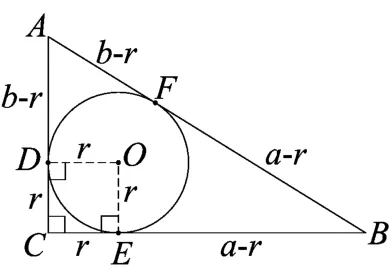
图9
分析 有学生直接用2013年人教版九上98页练习第2题的结论,得,由此得
有的学生依据“见切线,连半径”的思路构造正方形,如图9,根据切线长定理,不断“转移”边,建立关于r的方程a-r+b-r=c,解得r=
注 解答的途径不同,自然体现的思想方法就有别.前者的依据面积的分割法,而后者注意到相关边之间的联系与转化,融入了方程的思想.这两种都是基本的方法.新的问题来了:同一个内切圆的半径用两个不同的式子表示,有的同学就想追问个究竟.那如何证明此时,教师“留白”,供同学们课下继续探究.
当一道题的解法不唯一时,教师要珍重这个素材,点燃学生的思维之花,鼓励学生别出心裁.同时让学生懂得“三人行,必有我师”的道理,形成相互学习,取长补短,在集体中成长的品行,以此实现数学教育的育人目标.
1 刘家良.等一等等在何处[J].中学数学教学,2016 (4):11-13
2 刘家良.适时链接分类整合——首轮中考复习的实践与思考[J].中国数学教育(初中版),2014(6):63
2017-05-28)
