变式视角 例谈“任意”
2017-08-23福建省古田县第一中学兰诗全邮编352200
福建省古田县第一中学 兰诗全 (邮编:352200)
变式视角 例谈“任意”
福建省古田县第一中学 兰诗全 (邮编:352200)
高中数学中的“任意”一词在函数解析式、单调性、奇偶性、周期性、对称性等问题中常见常用,变式多样,丰富多彩,内含深刻.由于许多同学在数学解题中对“任意”一词理解不深,掌握不透,应用不活,从而严重影响解题思路与正确率.本文结合例子,从变式出发,多视角例谈数学中“任意”一词广泛而灵活的应用.
1 因为“任意”所以可以取“特殊”
例1 已知数列{an}中,对任意m、n∈都有,若,求a.4
解 由已知在am·an=am+n中,因为对任意m、n∈N+都成立,所以可取特殊值m=1,n=1.
例2 证明:函数f(x)=sinx2不是周期函数.
证明 假设函数f(x)=sinx2是周期函数, T是它的一个正周期.
即对任意x∈R,都有
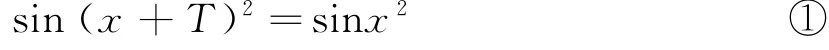
所以当x=0时,sinT2=0,得T2=kπ,T=kπ(k∈N+),代入①式,得

因此f(x)=sinx2不是周期函数.
反思 “任意”一词含有所有、一切的意思,具有一般性.在一般情况下都成立,那么在特殊(含在一般中)情况下也一定成立.这就极大方便于解题,只要有利于解题的特殊值都可以取,以上二例说明取什么特殊值这往往还很灵活,要有解题思维的全面性、前瞻性、逻辑性、严密性,方能取到有利于解题的特殊值.
2 因为“任意”所以图象有“对称”
例3 已知函数f(x)对任意实数x都有f(3+x)=f(3-x),如果方程f(x)=0恰有6个不同的实数根,求这些实数根之和.
解 因为函数f(x)对任意实数x都有f(3+x)=f(3-x),所以函数f(x)的图象是关于直线x=3对称的,因而每两个关于直线x=3对称的根的和为6,于是这6个根的和为3×6=18.
例4 证明:若函数y=f(x)在R上的图象关于点A(a,y0)和直线x=b(b>a)皆对称,则函数f(x)是R上的周期函数.
证明 已知函数y=f(x)在R上的图象关于点A(a,y0)和直线x=b(b>a)皆对称,所以对任意x∈R,有
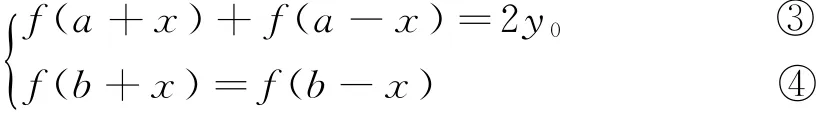
因为对任意x∈R,③,④都成立,所以可用R上的任何值替代x,反复利用③,④可得f[x+4(b-a)]=f[b+(x+3b-4a)]
=f[b-(x+3b-4a)]
=f[a+(3a-2b-x)]
=2y0-f[a-(3a-2b-x)]
=2y0-f[b+(b-2a+x)]
=2y0-f[b-(b-2a+x)]
=2y0-f[a+(a-x)]
=2y0-2y0+f[a-(a-x)]
=f(x).
即f[x+4(b-a)]=f(x),对任意x∈R恒成立.
所以4(b-a)是函数f(x)在R上的一个周期,即f(x)是周期函数.
反思:(1)若对∀x∈R,都有f(x+a)= f(b-x),则函数f(x)图象关于直线对称,反之也成立.
(2)若对∀x∈R,都有f(x+a)+f(bx)=2c,则函数f(x)图象关于点对称,反之也成立.
以上二点在解题中要灵活应用.其实,函数的单调性、奇偶性、对称性、周期性有其内在的联系,往往与“任意”一词密切相关.可以说,函数学习深不深透不透,很关键一点取决于对“任意”一词的理解与应用程度如何.
3 因为“任意”所以恒成立
x,试求出f(x)值域以外的唯一实数.
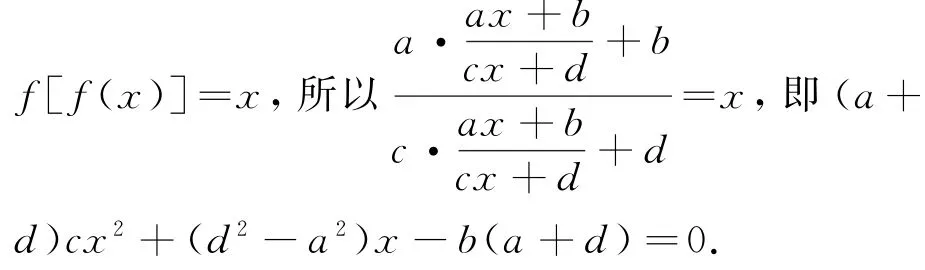
又f(19)=19,f(97)=97,即19,97是方程的两个根,
所以19,97是方程cx2+(d-a)x-b=0的两个根,故由韦达定理得,且1843.又由上d=-a,得a=58c,b=-1843c,d=-58c.
于是f(x)取不到58这个数,即58是f(x)值域外的唯一数.
(1)求实数a的值所组成的集合A,
解 (1)过程略,结果A={a-1≤a≤1};
x1+x2=a,x1x2=-2,所以x1-x2=
因为a∈[-1,1],所以x1-x2=
由于不等式m2+tm+1≥x1-x2对任意a∈A及t∈[-1,1]恒成立.
所以m2+tm+1≥x1-x2max,即m2+tm+1≥3恒成立.
记g(t)=mt+m2-2,则有g(t)≥0对任意t∈[-1,1]恒成立.
所以m≥2或m≤-2.
所以存在实数m,使得不等式m2+tm+1≥x1-x2,对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m m≥2或m≤-2}.
反思 (1)例5中,对于任意实数x,均有f[f(x)]=x,即(a+d)cx2+(d2-a2)x-b(a+d)=0对任意恒成立,
(2)“任意”常与“恒”“都”“一切”“所有”等联系在一起,解题中要善于等价转化,如例6,请读者深刻领会,灵活解题.
4 因为“任意”所以可代换
解 因为函数f(x)对定义域内的一切实数x都有


例8 证明:任何定义域关于原点对称的函数都可以表示为一个奇函数和一个偶函数的和.
证明 设定义域关于原点对称的函数为f(x),则f(x)与f(-x)(x∈D)同时有意义.
设存在一个奇函数g(x)和一个偶函数h(x),使
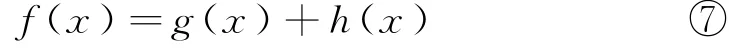
则f(-x)=g(-x)+h(-x),即

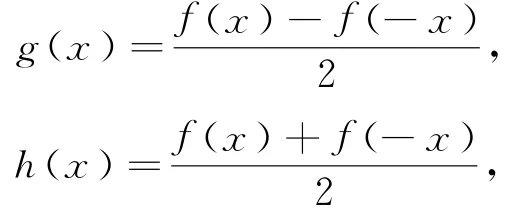
例9 已知f(x)是定义在R上的函数, f(1)=1,且对任意x∈R,都有f(x+5)≥ f(x)+5,f(x+1)≤f(x)+1.若g(x)=f(x)+1-x,求g(2002)的值.
解 由已知
g(x+5)=f(x+5)+1-(5+x)=f(x+5)-4-x≥f(x)+5-4-x=f(x)+1-x=g(x),
g(x+1)=f(x+1)+1-(x+1)≤f(x)+1-x=g(x),
所以g(x)≤g(x+5)≤g(x+4)≤g(x+3)≤g(x+2)≤g(x+1),
即g(x+1)=g(x)对任意x∈R都成立.
所以g(x)是周期为1的周期函数.
即g(2002)=g(1)=1.
反思 在实际教学中发现很多同学无法理解以上数例,追根溯源在于没有正确理解并应用好“任意”二字.既然函数f(x)对定义域内的任意实数x都有

下面再给出如下二个经典练习:
1.定义在R上的函数f(x),对任意x、y∈R,满足f(x+y)=f(x)+f(y),且当x>0时,f(x)<0.
(1)证明:f(0)=0,
(2)证明:f(x)为奇函数,
(3)证明:f(x)为(-∞,+∞)上的单调减函数.
2017-06-16)
