对初中数学应用题教学的一点思考

缪辉平

【摘要】在实际生活中，方案设计问题也是多种多样，如裁料方案、测高方案、调运方案.有的方案设计要涉及可行性的讨论和最佳性的选择，日新月异的社会变化、丰富多彩的实际生活，要求应用题设计要与时俱进，只要我们了解了这个新的趋势，在数学教学中适当加强训练，就可以以不变应万变，把握好成功的机会.

【关键词】初中数学；应用题；教学思考

科学地认识事物就要抓住事物的本质，那么列方程解应用题的本质是什么呢？很显然，列方程（组）是关键.所谓列方程（组）解应用题是一个“实际”问题，以文字表达形式出现，然后，运用数学方法将应用题的内涵符号化成为一个方程（组），再解所列方程（组）从而应用题得解，因此，在应用题的教学时，应把难点放到分析題意列出方程（组），并让学生熟练掌握应用题符号化这一步骤，这样方程（组）就列出了，当然学生刚刚接触应用题时可能有些难度，但按照教材的编排，在学习列方程（组）解应用题之前就学习了用代数式表示各种各样背景下的实际问题，也学习了解方程和解方程组，学习了行程、速度、时间之间的关系，学习了工作总量、工作效率、工作时间之间的关系，学习了销售中的本金、利润、利率之间的关系，等等.

初中数学中的应用题是建立在小学的基础上的，而且是从“行程问题”入手，因此，在一开始进行“行程问题”的教学时就必须强调要求画“s，v，t”表格：

来帮助分析，且要掌握好公式：路程（s）=速度（v）×时间（t），而且初中阶段的大多数应用题都可以借助“s，v，t”表格来帮助分析，如“工程问题”.

例1A，B两地相距360 km，甲、乙两辆车分别从A，B两地同时出发相向而行，甲车的速度是70 km/h，乙车的速度是50 km/h，求甲、乙两车出发后经过几小时相遇？

解设甲、乙两车出发后经过x小时相遇.

分析：（一）找等量关系：① 甲车的行驶时间（t甲）=乙车的行驶时间（t乙）；

② 甲车的行驶路程（s甲）+乙车的行驶路程（s甲）=360.

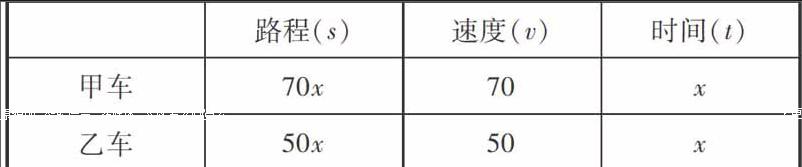
（二）画“s，v，t”表格：

（三）列方程：

因为等量关系① 甲车的行驶时间（t甲）=乙车的行驶时间（t乙）在画“s，v，t”表格时已经用过.因此，只能根据等量关系②甲车的行驶路程（s甲）+乙车的行驶路程（s乙）=360.列方程得

70x+50x=360.

解这个方程得x=3.

答：甲、乙两车出发后经过3小时相遇.

强调：① 认真理解题意，弄清题目中事件发生过程及其各个量之间内在的等量关系，每个等量关系只允许用一次；

② 画“s，v，t”表格，并填写“s，v，t”表格，这样可大大地减少犯低级错误；

③ 根据未用过的等量关系来列方程.

并且在以后所有应用题教学引导中都要这样“强调”，让学生形成思维习惯.

例2A，B两地相距35 km，甲从A地向B地出发5 km，乙在A地发现甲忘记带某文件立即追送，交给甲后立即返回A地，当乙返回A地时，甲恰好到达B地，乙每小时比甲多行5 km，求两人的速度.

解设甲的速度是x km/h.

分析：（一）画行程图，找出等量关系.在这必须认真理解题意，弄清楚整个事件发生过程，才能画出行程图.

从行程图中看到：甲从C点到D追及点的时间（t甲CD）与乙从A点到D追及点的时间（t乙AD）是相等的，乙从D追及点返回A点的时间（t乙DA）与甲从D追及点到B点的时间（t甲DB）也是相等的.即t乙AD=t乙DA=t甲CD=t甲DB.

因此，CD=DB=15，AD=AC+CD=20.

找到等量关系：① 乙的速度（v乙）=甲的速度（v甲）+5；

② 甲行进15 km的时间（t甲15）=乙行进20 km的时间（t乙20）.

（二）画“s，v，t”表格：

解这个方程得x=15.

经检验得x=15是所列方程的解.因此，x+5=20.

答：甲的速度是15 km/h，乙的速度是20 km/h.

此题中列方程要用到的等量关系②甲行进15 km的时间（t甲15）=乙行进20 km的时间（t乙20）没有明确表示出来，是隐藏于题目内的，需要认真地理解题意，并要借助行程图才好找.

列方程解应用题的一般基本步骤为：

（一）审题（主要完成如下三方面的工作）：

1.分析条件（对条件要进行归纳分类），认真理解题意，弄清题目中事件发生过程及各个量之间内在联系，可借画“s、v、t”表格帮助理解.

2.明确已知量和未知量.

3.找出等量关系，每个等量关系只允许用一次.

（二）解题的实施：

1.设未知数（或称设元）.

2.根据等量关系列出方程（组）.

3.解方程（组），并检验.

4.答.

学生列方程（组）解应用题的困难主要来自如下三方面：

第一，审题没有养成习惯，对文字图形理解能力低下，缺乏生活实践知识，根本弄不清题意，有的虽然审题，但审题缺乏逻辑性和系统性.其突出表现在于对审题的基本要求是什么不明确，对题目中的条件不习惯于归纳分类.因而，造成考虑问题不是全局化、透彻化，而是孤立的、表面地理解条件，甚至遗漏条件.

第二，用代数式表示各种实际问题中的量、解方程（组）等与基础知识脱节，比如，弄不清楚销售中的销售额、标价、售价、本金、利润、利率之间的关系.

第三，不明确（或没注意）列方程的基本标准，列出与实际意义不相符（错误）的方程.我们常常发现学生列出来的方程两边的意义不同，也发现一个代数式所表示的意义混乱，如，把速度与时间相加（或相除）的代数式.

鉴于上述三点，在教学上应采取什么措施以便降低错误率呢？我认为，应注重如下几方面.

1.应坚持系统性原则，可以这么认为，列代数式的训练是列方程解应用题的前奏，故应该全力争取使学生在列代数式阶段能具备较完善的由语言信息转化到数学式子（代数式）的能力，事实上，现行教材已经有足够的内容使之达到这个要求的.就是列方程解应用题本身看，也是分阶段的（如，一元一次方程，二元一次方程，一元二次方程，二元二次方程等）.在诸多阶段中，应该算一元一次方程的应用题最为关键，若这一关过不好，很难保证今后学习会顺利.因此，教师在整个初中数学教学上应全面考量.

2.要严格审题程序，弄清题目中事件发生过程及其各个量之间内在的联系，这方面教师在平时教学中应落实提高学生的文字理解能力，准确地将文字语言转化成数学语言.

3.明确列方程解应用题的基本要求.主要明确三点：（1）在同一方程里，两边的意义要相同，如不要一边是距离，另一边又是时间；（2）同一方程里的各项的单位要统一，如不要一些是小时，一些又是分钟；（3）方程两边的数量要相等，符合实际意义等.

4.注意总结方程应用题的类型的基本关系式.如，路程=速度×时间；工作量=效率×时间；工作总量=各部分工作量之和等；利润=本金×利率=营业额-本金.

通过数学建模，既考查从数学的角度观察、思考和分析实际问题的能力，又考查对相关知识（包括数学的、生活的、社会的、自然的，乃至文化的多方面的知识）和技能的理解和掌握程度.从而能比较好地反映学生对信息的接收、加工和输出能力，达到有效考查综合素质的目的.所以，平时要加强运用数学意识的培养，学会数学地思维.