钢丝绳芯橡胶输送带本构模型参数辨识与变化规律分析

陈洪月， 张 坤， 李恩东

(1.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000；2. 辽宁工程技术大学 国家地方联合矿山液压技术与装备工程研究中心，辽宁 阜新 123000；3. 煤炭工业协会 高端综采成套装备动力学测试与大数据分析中心，辽宁 阜新 123000)

钢丝绳芯橡胶输送带本构模型参数辨识与变化规律分析

陈洪月1,2,3， 张 坤1， 李恩东1

(1.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000；2. 辽宁工程技术大学 国家地方联合矿山液压技术与装备工程研究中心，辽宁 阜新 123000；3. 煤炭工业协会 高端综采成套装备动力学测试与大数据分析中心，辽宁 阜新 123000)

橡胶输送带模型参数辨识是研究大型带式输送机动态特性的关键问题。首先采用黏弹性动力学理论和傅里叶级数拟合方法推导并建立了橡胶输送带标准固体模型的参数辨识方程，并通过实验对辨识方程进行了验证；然后对不同加载条件下实验数据的辨识结果进行了二次多项式拟合，分别获得了加载位移幅值、频率对输送带本构模型参数的影响规律。结果表明：随着加载幅值的增大，黏性系数具有先减小后增大的变化规律，弹性模量E1小幅度增大、E2大幅度增大趋势，随着加载频率的增大，黏性系数、弹性模量E1、E2均逐渐减小；最后，通过实验对拟合公式的准确度进行了验证。

橡胶输送带; 标准固体模型; 阻尼特性; 参数辨识

橡胶输送带的力学特性分析是研发大距离、大运量及节能输送机的关键[1-2]，现有的输送带本构关系多采用Vogit-Kelvin 模型和三元件标准固体模型描述，特别是三元件标准固体模型既能够表达输送带的瞬态响应，又能表达蠕变和松弛特性，且模型的描述精度较高[3-4]，所以常被用于描述输送带及其类似黏弹性材料的动态行为。如：文献[5]采用标准固体模型建立了输送带压陷阻力及能耗方程，对不同条件下的输送带能耗进行了计算。文献[6]提出一种等效的固体模型，并通过实例分析验证了模型的准确性。文献[7]采用标准固体模型研究了桩的动力学响应。文献[8]通过实验测试数据计算了输送带动态弹性模量、黏滞系数、弹性伸长率等参数。文献[9]采用标准固体模型对带式输送机启动过程的动态特性进行了分析。文献[10-11]分别采用傅里叶级数和高斯函数对橡胶输送带的动力学参数进行了辨识和预测。文献[12]采用标准固体模型研究了刚性托辊与输送带间的接触力学问题。文献[13]采用标准固体模型研究了各向同性板的瞬态动力学特性；文献[14]提出一种改进的标准固体模型，并采用蠕变实验对模型进行了验证。

标准固体模型非常适合描述输送的黏弹性动力特征，但它的蠕变和松弛均具有指数规律，并且模型参数测定较为困难，因而限制了该模型在带式输送机动态特性分析中的应用，本文为了对橡胶输送带本构模型参数进行辨识，首先在时域上分析交变应变作用下本构模型的应力响应，采用黏弹性材料动态恢复力的傅里叶级数辨识理论，推导应力响应方程中的系数和本构模型参数的求解方程，最后采用实验方法对标准固体模型参数辨识精度进行验证。

1 标准固体模型参数辨识

输送带属于典型的黏弹性材料，根据文献[15]知，黏弹性材料的标准固体模型，如图1所示。其本构模型可由式(1)表示。

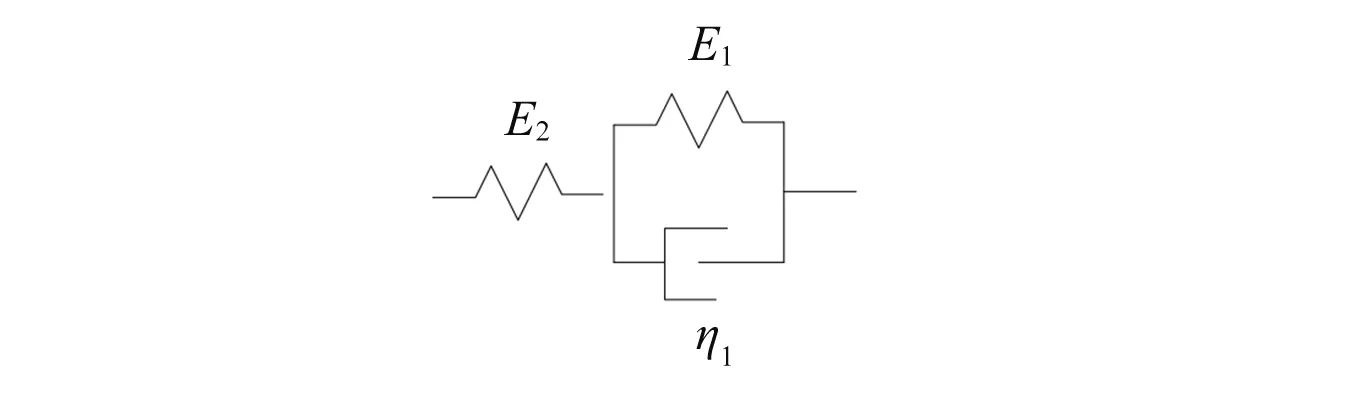
图1 标准固体模型Fig.1 Standard solid model

(1)

式中：

(2)

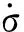
当输送带的外载为动应变作用时，

ε=Asinωt+ε0

(3)

式中：A为应变幅值，ω为加载角速度，ε0为初始应变。

将式(3)代入式(1)有：

(4)

对式(4)求解，得：

(5)

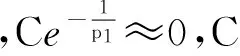
则动态应变下的应力为

(6)

设输送带负载为位移激励，

x=Msinωt+x0

(7)

式中：x0为加载的初始位移；M为加载位移幅值；ω为加载频率。根据几何方程

(8)

式中：L为输送带长度。

可得应变幅值和初始应变

于是式(6)变为

(9)

令：

则式(9)变为

(10)

输送带在位移激励下的动态力可表示为

F=σ(t)S

(11)

式中，S为输送带的横截面积。

将式(10)代入式(11)得：

(12)

简化后得：

F=a0+a1*cosωt+b1*sinωt

(13)

式中：

(14)

(15)

(16)

因式(13)可等同为1阶傅里叶级数形式，所以可采用傅里叶级数对输送带的外部载荷F进行拟合，求得傅里叶级数的系数a0、a1、b1，再求解标准固体模型的三个参数，过程如下：

由式(14)，可得：

(17)

联系式(15)、式(16)整理后得：

(18)

解:

(19)

(20)

将式(17)、式(19)、式(20)代入式(2)后，整理可得标准固体模型参数的辨识模型为：

(21)

(22)

(23)

2 标准固体模型参数辨识及验证

GB/T 15902—2009规定，对于钢丝绳芯输送带的动态加载实验中，动态载荷范围通常为输送带破断载荷的10%左右，加载应变范围约0.002～0.004 5，这相当于输送带实际工作过程中的最小张力和最大张力值[16]。

实验材料选用ST1600型钢丝绳输送带，其钢丝绳芯直径为5 mm，上下覆盖层橡胶厚度分别均为6 mm，实验用输送带的带宽75 mm，厚17 mm，输送带横截面积S为1 275 mm2，实验台夹具间带长L为1 000 mm，在确定的实际工况下，本实验中所用输送带的应变范围为2～4.5 mm，采用电子万能拉伸实验台对输送带进行加载实验。

实验过程中对输送带进行正弦位移加载，频率f=0.1 Hz、幅值M=1.4 mm、初始位移x0=1.9 mm，加载函数为：

x=1.4sin(0.2π*t)+1.9

mm

根据式(13)采用MATLAB中的傅里叶级数拟合法对实验曲线进行拟合，可得：a0=3 763.3、a1=4 600.5、b1=3 422.3，将其与M、x0、L、S及ω同时代入式(21)～式(23)后，求得标准固体模型参数η1=4 907.34 MPa·s、E1=1 684.43 MPa、E2=20 259.84 MPa。

实验曲线与拟合曲线的对比，如图2所示。两条曲线的确定性系数达到了0.999 7，说明两条曲线的吻合较好。

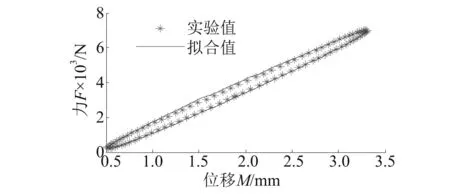
图2 实验与拟合曲线Fig.2 Experiment and fitting curve

图3为实验值与拟合值的差值，由图3可知：输送带在加载的误差为正值，最大误差为221 N，在卸载段的误差为负值，最大误差为-245 N，拟合误差相对较小，能够满足工程计算要求。

图3 实验值与拟合值误差Fig.3 The experimental values and the fitting value error

3 本构模型参数变化规律

由于橡胶输送带具有黏弹性的特点，所以输送带的外负载变化时，其固体模型参数η1、E1、E2的大小也是不同的，因此研究不同加载条件下橡胶输送带的本构模型参数对研究带式输送机的动态特性具有实际意义，为此，根据“2”节中确定的输送带实际工况下的应变范围，对不同加载条件下的输送带的动态特性进行测试，再通过“2”节中的辨识方法对模型参数进行辨识，最后通过辨识结果研究模型参数的变化规律。

3.1 加载幅值对模型参数的影响规律

不同加载幅值条件下的输送带模型参数的辨识结果，如表1所示。

在表1中，输送带的加载频率均为0.1 Hz，加载最小位移为0.5 mm，最大位移分别为2 mm、2.5 mm、2.7 mm、3 mm、3.5 mm、4 mm、4.5 mm，由辨识结果可知：当加载频率不变，随着加载位移的逐渐增大，黏性系数先减小后增大；弹性模量E1具有逐渐减小的趋势，但变化量较小；弹性模量E2具有逐渐增大的趋势，而且变化量较大，说明随着加载位移的增大，输送带的刚性越强。

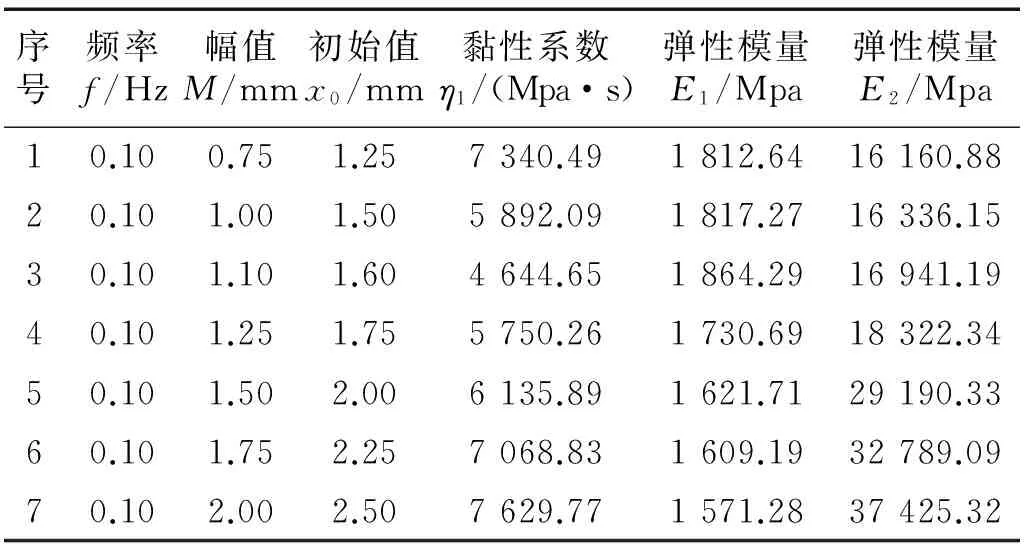
表1 不同加载幅值条件下输送带固体模型参数

为了揭示加载幅值M对模型参数影响规律，并实现对不同加载幅值M条件下输送带模型参数进行预测，以加载幅值M为变量，采用多项式对表1中的模型参数进行函数拟合，结果如下：

η1(M)=(4.78M2-12.67M+13.92)×103

(24)

E1(M)=(-0.04M2-0.14M+1.98)×103

(25)

E2(M)=(9.32M2-6.22M+14.01)×103

(26)

以上三个拟合曲线与原始数据间的确定性系数分别为0.82、0.85、0.94，由确定性系数可知：弹性模量E2的曲线拟合效果相对好、阻尼系数η1的拟合效果相对较低。

3.2 加载频率对模型参数的影响规律

为了研究加载频率对输送模型参数的影响，分别设置加载频率为0.02 Hz、0.05 Hz、0.08 Hz、0.10 Hz、0.12 Hz、0.15 Hz对输送带进行加载实验，辨识结果，如表2所示。

表2 不同加载频率条件下输送带固体模型参数

由表2可知：随着加载频率的增大，输送带的黏性系数、弹性模量E1和E2均逐渐减小，特别是弹性模量E2变化的更为明显。

为了揭示加载频率f对模型参数的影响规律，以加载频率f为变量，采用多项式进行函数拟合，结果如下：

η1(f)=(-8.66f2-7.34f+6.47)×103

(27)

E1(f)=(-1.9f2-0.25f+1.68)×103

(28)

E2(f)=(1 183f2-477.4f+56.54)×103

(29)

以上三个拟合曲线与原始数据间的确定性系数分别为0.98、0.99、0.96，说明两者间存在着良好的近似度。

4 拟合函数预测精度验证

为了对所得到的拟合式(24)～式(26)进行验证，以频率f=0.1 Hz、幅值M=1.45 mm、初始位移x0=1.95 mm为加载参数对输送带进行动态加载实验，根据“2”节中的方法，可辨识出模型参数具体值；将幅值M=1.45 mm代入式(24)～式(26)，可得到模型参数的预测值，将辨识结果与预测结果进行对比，如表3所示。

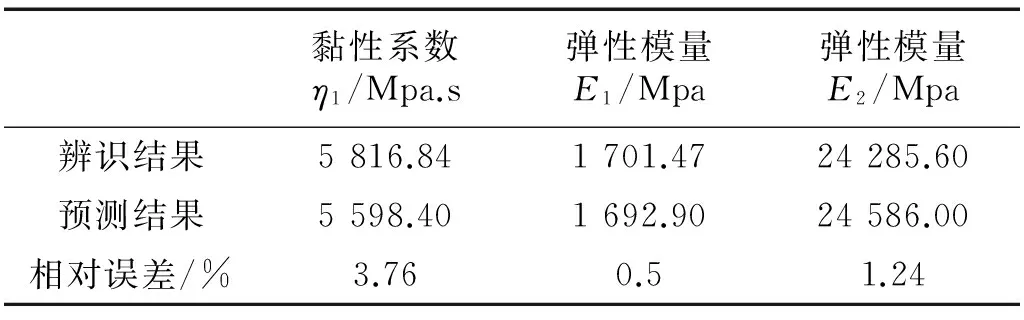
表3 模型参数对比

由表3可知：黏性系数η1的辨识值与预测值间的误差最大，但其相对误差为3.76%，说明拟合公式具有较好的预测精度。

为了对所得到的拟合式(27)～式(29)进行验证，设定实验加载参数f=0.11 Hz、M=1.25 mm、x0=1.75 mm，进行输送带的加载实验和模型参数辨识，并采用式(27)～式(29)对f为0.11 Hz时，输送带模型参数进行预测，辨识结果与预测结果对比，如表4所示。

表4 模型参数对比

表4中的弹性模量E1的预测误差最大，约为5.4%，说明拟合公式具有较高的预测精度。

5 结 论

(1) 建立了含初始位移的动态应变作用下橡胶输送带标准固体模型的应力响应方程，通过黏弹性材料的傅里叶辨识模型，建立了标准固体模型参数的辨识方程；采用数值分析和实验相结合的方法对标准固体模型参数的辨识方程的准确性进行了验证。

(2) 通过对输送带进行不同加载条件下的模型参数辨识结果分析，得出：当加载频率不变时，随着加载幅值的增大，黏性系数具有先减小后增大的变化规律，弹性模量E1具有小幅度增大、E2具有大幅度迅速增大的规律；当加载幅值不变时，随着加载频率的增大，粘性系数、弹性模量E1、E2均逐渐减小，但E2变化的更为明显。

(3) 分别以加载幅值、加载频率为变量，采用多项式拟合方法对输送带的模型参数进行拟合和预测，并通过实验数据的辨识结果对比，验证了拟合公式具有较好的预测精度。

[1] 宋伟刚.通用带式输送机设计[M].北京:机械工业出版社,2005.

[2] 侯红伟.输送带黏弹性模型分析[J]. 煤矿机电,2014(6):1-3. HOU Hongwei. Analysis of viscoelastic model of conveyor belt[J]. Coal Mine Electromechanical, 2014(6):1-3.

[3] 毛君,解本铭,孙国敏.带式输送机动态设计理论与应用[M].辽宁科学技术出版社，1996.

[4] 王繁生. 带式输送机柔性多体动力学分析方法研究[D]. 徐州：中国矿业大学, 2010.

[5] 杨彩红,毛君,李春林. 输送带压陷阻力的研究[J].煤炭学报,2010,35(1):149-454. YANG Caihong, MAO Jun, LI Chunlin. Study of indentation resistance of conveyor belt[J]. Journal of China Coal Society 2010, 35(1):149-454.

[6] 徐赵东,周洲,赵鸿铁,等. 黏弹性阻尼器的计算模型[J].工程力学,2001,18(6):90-95. XU Zhaodong,ZHOU Zhou,ZHAO Hongtie,et al. The computational model of viscoelastic dampers[J]. Engineering Mechanics,2001,18(6):90-95.

[7] 孙昱,王奎华,谢康和. 标准线性固体土模型条件下桩的动力响应分析与应用[J]. 计算力学学报,2004,21(3):330-337. SUN Yu, WANG Kuihua, XIE Kanghe. Vibration of pile with normal linear solid shape and its application[J]. Chinese Journal of Computational Mechanics, 2004,21(3):330-337.

[8] 刘月琴,孙连生,黄松元. 输送带力学性能参数测试方法的研究[J]. 橡胶工业,1994,41(3):174-177.

LIU Yueqin, SUN Liansheng, HUANG Songyuan. Study on the conveyor belt mechanical properties test method[J]. Rubber Industry, 1994,41(3):174-177.

[9] 魏振华,侯红伟,宋兴元. 带式输送机三元件固体模型启动过程动态分析[J]. 煤矿机电,2015(1):53-57. WEI Zhenhua,HOU Hongwei,SONG Xingyuan. Dynamic analysis with three element solid model of belt conveyor in starting process[J]. Colliery Mechanical & Electrical Technology, 2015(1):53-57.

[10] 陈洪月,王鑫,钟声,等.橡胶输送带迟滞特性分析与恢复力模型参数预测[J].煤炭学报, 2015,40(12):2995-2999. CHEN Hongyue,WANG Xin,ZHONG Sheng, et al. Hysteresis characteristic analysis of rubber conveyor belt and parameter prediction of restoring force model[J]. Journal of China Coal Society, 2015,40(12):2995-2999.

[11] 陈洪月,白杨溪,张瑜,等. 橡胶输送带恢复力模型辨识与参数预测[J].中国机械工程,2016,27(6):810-815. CHEN Hongyue, BAI Yangxi, ZHANG Yu, et al. Model identification and parameter forecasting of rubber conveyor belt restoring force[J].China Mechanical Engineering, 2016,27(6):810-815.

[12] 王繁生. 基于黏弹性材料标准固体模型的接触问题数值方法研究[J]. 机械科学与技术,2015,34(1):65-69. WANG Fansheng. Study on the numerical method of the contact problem based on the standard solid model of viscoelastic material[J]. Mechanical Science and Technology for Aerospace Engineering,2015,34(1):65-69.

[13] ROSSIKHIN, Y A， SHITIKOVA M V. The analysis of the impact response of a thin plate via fractional derivative standard linear solid model[J]. Journal of Sound and Vibration,2011,33(9): 1985-2003.

[14] CHUNG C W, BUIST M L. A novel nonlinear viscoelastic solid model[J]. Nonlinear Analysis Real World Applications,2012,13(3): 1480-1488.

[15] 张义同.热弹性性理论[M].天津:天津大学出版社,2002.

[16] 输送带弹性伸长率和永久伸长率的测定及弹性模量的计算：GB/T 15902—2009[S]. 北京：中国标准出版社, 2009.

Parameter identification and analysis on the constitutive model of wire rope rubber conveyor belts

CHEN Hongyue1, 2,3, ZHANG Kun1, LI Endong1

(1.College of Mechanical Engineering, Liaoning Technical University, Fuxin 123000,china;2.National and local combined mining technology and equipment Engineering Research Center Liaoning Technical University, Fuxin 123000,china;3. Dynamic Research for high-end complete Integrated Coal Mining Equipment and Big Data Analysis Center, China National Coal Association , Fuxin 123000,China )

The parameter identification of a rubber conveyor belt model is the key problem in researching the dynamic characteristics of large belt conveyors. The parameter identification equation of the standard solid model for the rubber conveyor belt was derived by employing the viscoelastic dynamics theory and the Fourier series fitting method, and was validated by experiments. The quadratic polynomial fitting was performed on the identification results of experimental data under different load conditions. The influences of the load displacement amplitude and frequency on the constructive model parameters of the conveyor belt were analysed. The results show that with the increase of load amplitude, the viscosity coefficient first decreases and then increases, the elastic modulusE1increases by a small amplitude, and the elastic modulcesE2increases by a large amplitude quickly. With the increase of load frequency, the viscosity coefficient, theE1andE2decrease gradually. The accuracy of the fitting equations was validated by experiments.

rubber conveyor belt; standard solid model; damping characteristics; parameter identification

国家自然基金(51404132)

2016-07-06 修改稿收到日期：2016-10-21

陈洪月 男，博士，副教授，1982年生

张坤 男，博士生，1990年生

TB33

A

10.13465/j.cnki.jvs.2017.14.037