多失效模式下多状态伺服转塔刀架系统频率可靠性分析
2017-07-19刘晨曦
刘晨曦, 陈 南
(1.江苏大学 机械工程学院,江苏 镇江 212013;2.东南大学 机械工程学院,南京 211189)
多失效模式下多状态伺服转塔刀架系统频率可靠性分析
刘晨曦1, 陈 南2
(1.江苏大学 机械工程学院,江苏 镇江 212013;2.东南大学 机械工程学院,南京 211189)
根据频率响应函数特性曲线的连续性,传统频率可靠性分析中仅将共振区与非共振区二分化值得商榷。提出了多失效模式下多状态频率可靠性分析方法,综合考虑影响系统固有频率各结构参数的随机性、激励频率的随机性,应用Monte Carlo仿真估计出系统频率可用度,并根据相关性分析识别各结构随机参数对系统频率可靠性的影响。将该方法用于基于多体系统传递矩阵法所建立的伺服转塔刀架系统动力学模型中,研究了其频率可用度以及与系统状态最为相关的结构参数,所得分析结果为系统优化设计提供了依据。
伺服转塔刀架;多失效模式;多状态;频率可靠性;相关性
伺服转塔刀架(以下简称为刀架)是一种利用伺服电机驱动工位快速转换,依靠液压锁紧的中高档数控转塔刀架。刀架配备在数控车床上,作为切削加工的动作执行部件参与制造生产,直接承受着动态切削载荷,其本身的动态性能是车床整体动态性能的重要部分。当刀架系统所承受的动载频率接近其固有频率时将会发生共振,从而严重影响车床的加工精度甚至对系统稳定造成破坏性的危害,因此需要对刀架系统进行频率可靠性分析,评估系统不发生共振失效的概率。系统结构参数中,零件的材料密度、制造尺寸以及装配部件的配合尺寸、位置尺寸等均存在一定的不确定性,相应地将带来整个刀架系统固有频率的不确定性,而不同随机参数所产生的影响程度不同,如何定量评价影响的高低将对系统优化提供指向。
以往对系统频率可靠性研究中,通常根据激励频率与固有频率的差值[1-3]或者比值[4]是否在特定区间范围内来建立共振失效准则;对于不同的结构系统,所定义的区间范围往往不同[5-8],但状态函数的建立均基于“共振准则”,即根据激励频率所处位置二分为共振区或安全区,相应地以评定系统失效或正常。事实上,频率响应特征函数是一条平滑的连续曲线,对某一阶固有频率而言,激励频率与之越邻近系统响应放大因子越大,越远离则不存在放大效应,而在理想共振与理想安全之间存在着中间过渡状态。因此,本文综合考虑结构参数以及激励频率的随机性,提出了多失效模式下多状态频率可靠性分析方法。
多状态特性的引入带来了分析问题维度和复杂性的增加。Monte Carlo仿真作为基于随机试验的数值模拟方法,具有通用性好、收敛速度与基本随机参数维数、功能函数复杂程度无关的优点,因此特别适于多状态系统可靠性分析[9]。本文选取可用度作为系统频率可靠性的评价特征量,采用Monte Carlo仿真方法进行估计,并根据相关性分析识别各结构随机参数对系统频率可靠性的影响。
1 多失效模式下多状态频率可靠性分析方法
1.1 定义及必要性说明
根据频响函数特性曲线,激励频率和系统固有频率的比值与振幅放大系数所对应的关系反映了系统动态特性。因此,将固有频率左、右邻域划分为不同的子区间,用于描述系统响应的优劣状态。
定义一 (多状态)对系统第i阶固有频率ωi,将频率范围(0,ωi]∪[ωi,+∞)划分为ni个子区间,子区间j对应频率范围
(1)
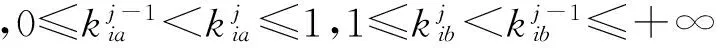

以下将通过一个典型单自由度弹簧-质量系统来阐述频率可靠性分析中引入多状态特性的必要性。为方便说明,这里假定质量、刚度参数均为定值,仅考虑两类服从不同分布规律的随机激励频率,其中Y1服从正态分布Y1~N(μ,σ2),Y2服从均匀分布Y2~U(0,σ/0.135 5)。系统固有频率为ω,根据传统共振准则界定失效域为(ka·ω,kb·ω),恰好处在区间(μ+σ,μ+2σ),如图1所示。显然在两类激励作用下,系统处于失效状态的概率分别为区域A1、B1的面积,均为13.55%。因此,依据正常、失效状态二分化,将认为该系统在两类随机激励频率下具有相同的频率可靠性。
根据本文提出多状态定义,由振幅放大因子将系统划分为完全正常、临界、完全失效3个离散状态,对应激励频率所处子区间分别为(0,μ]∪[μ+3σ,+∞)、(μ,μ+σ]∪[μ+2σ,μ+3σ)、(μ+σ,μ+2σ),如图2所示。同理,概率密度函数曲线在各子区间下的面积即为系统处于不同状态的概率。则在Y1、Y2两类激励下,系统处于临界状态的概率对应区域A2、B2面积,分别为36.3%、27. 1%。显然传统准则下将系统频率可靠性视为等同有失妥当。
从以上说明可以看出,多状态特性的引入将使得系统频率可靠性模型更为精细化。
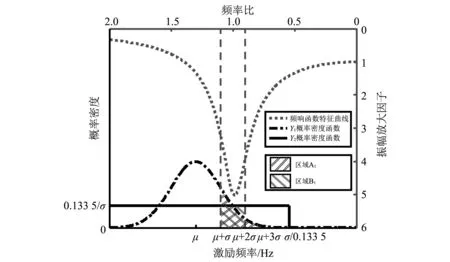
图1 单自由度系统传统两状态划分Fig.1 Traditional two-state divide of a single-degree-of-freedom system
多自由度系统存在多阶固有频率,在传统频率可靠性分析中,激励频率处于任意一阶固有频率的共振区时,即认为系统将产生共振失效。换言之,系统失效与否的判定基于各阶固有频率下失效判定的串联结构。同理,在引入“多状态”特性后,以下将定义“多失效模式”的概念以确定系统状态值。
定义二 (多失效模式)多自由度系统存在多阶固有频率ω1,ω2,…,根据定义一,对任意随机激励频率相应地可以得到系统在各阶固有频率下的状态判定值分别为g1,g2,…,且满足各数值之间相互独立。因此,系统状态g可视为各阶固有频率下状态判定值的或门运算[10],满足关系式
g=max(g1,g2,…)
(2)
式中:第i阶固有频率下的状态判定值满足gi∈(1,2,…,ni);假定各阶固有频率下判定值的离散状态个数相等,即具有n1=n2=…n,则系统状态满足g∈(1,2,…,n)。

图3 多状态“或”门Fig.3 Multi-state OR Gate
1.2 可靠性分析
考虑系统因材料、加工制造、装配等因素所导致固有频率特性的不确定性,定义结构随机参数向量X=
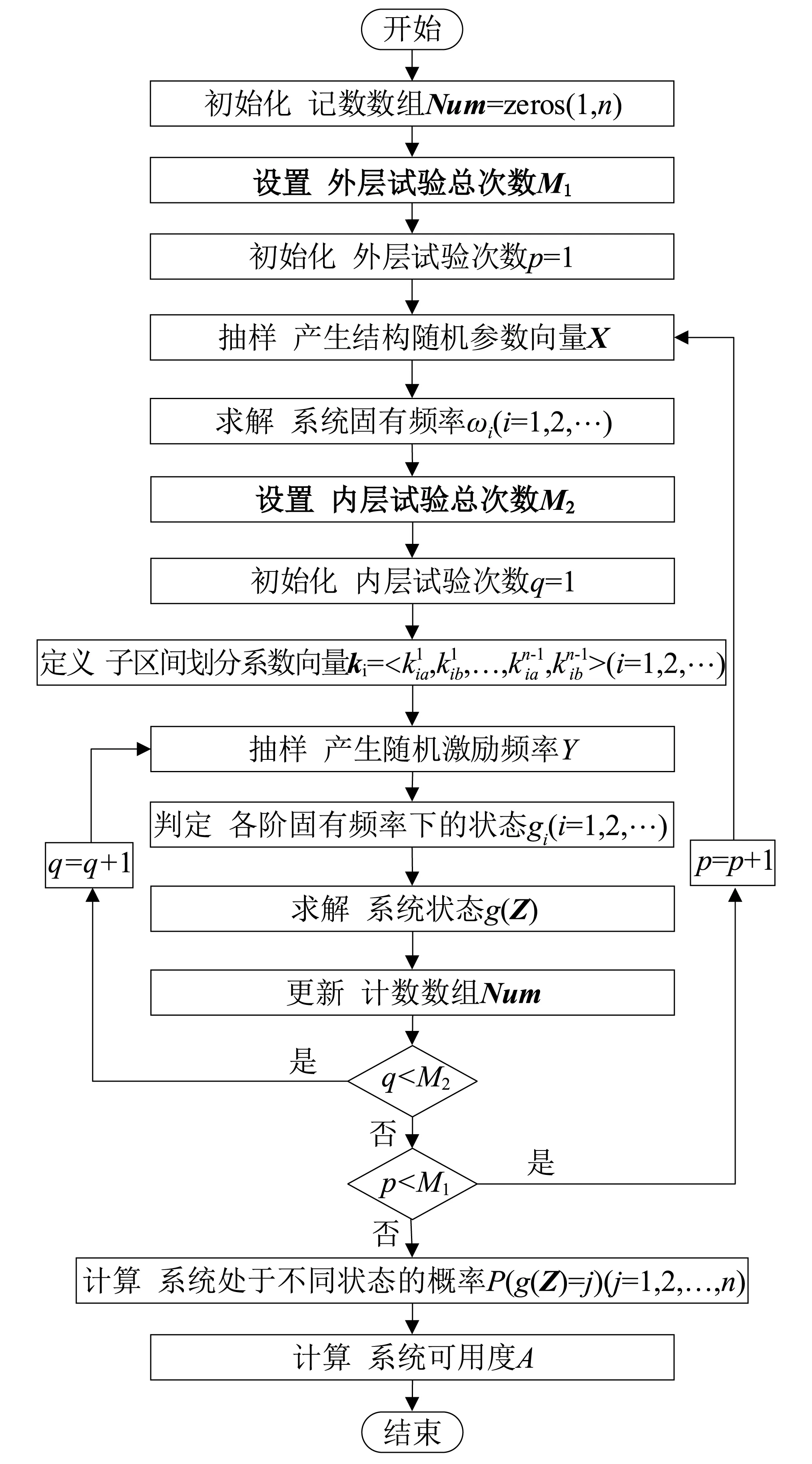
图4 基于Monte Carlo仿真频率可靠性分析流程图Fig.4 Frequency reliability analysis flow chart based on Monte Carlo simulation
整个试验流程可以描述为:
(1)定义计数数组Num1×n,并将所有元素均初始化为零,维数n为系统具有的离散状态个数,第j个元素对应系统处于状态j的次数;
(2)设置外层试验总次数M1,并初始化外层试验次数p=1;
(3)在一次外层试验中,根据随机参数所具有的已知分布规律抽样产生结构随机参数向量X,以健全系统动力学模型并求解系统固有频率ωi(i=1,2,…);

(5)在一次内层试验中,根据已知的分布规律抽样产生随机激励频率参数Y,再由式(2)求解本次试验的系统状态g(Z);
(6)更新计数数组Num:若本次试验判定系统处于状态j,则将Num中第j个元素数值增1,其他元素数值不变;
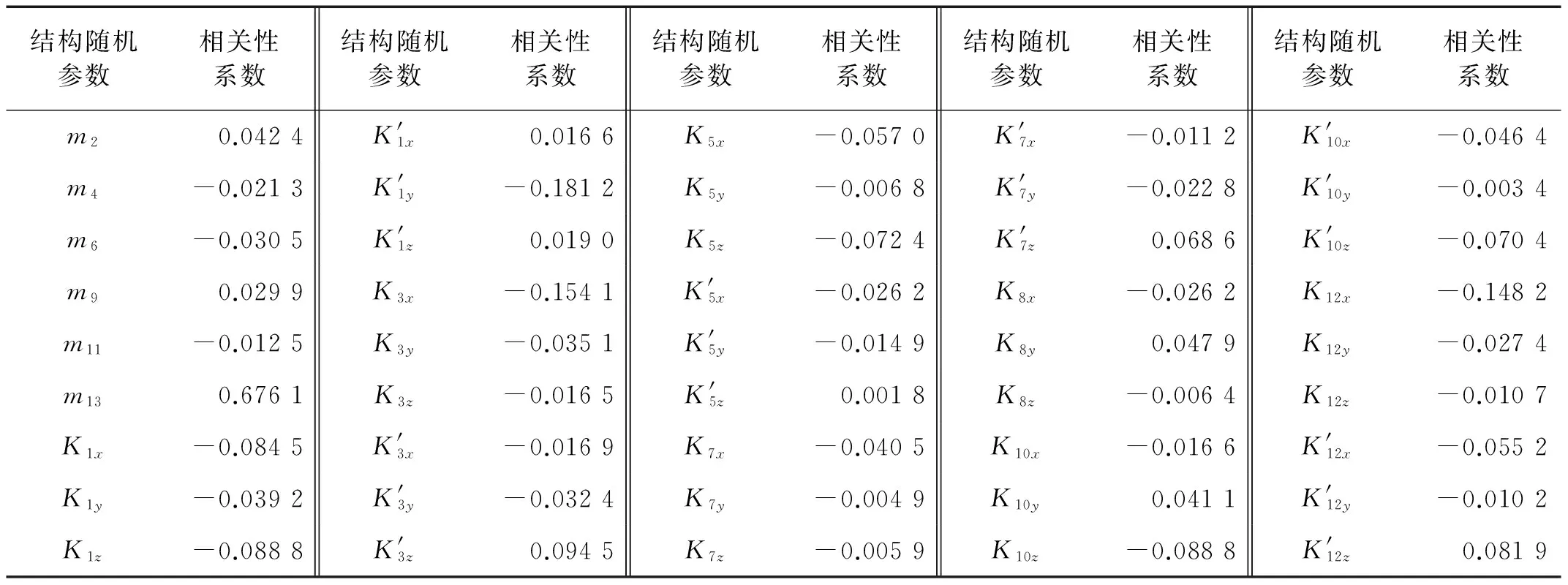
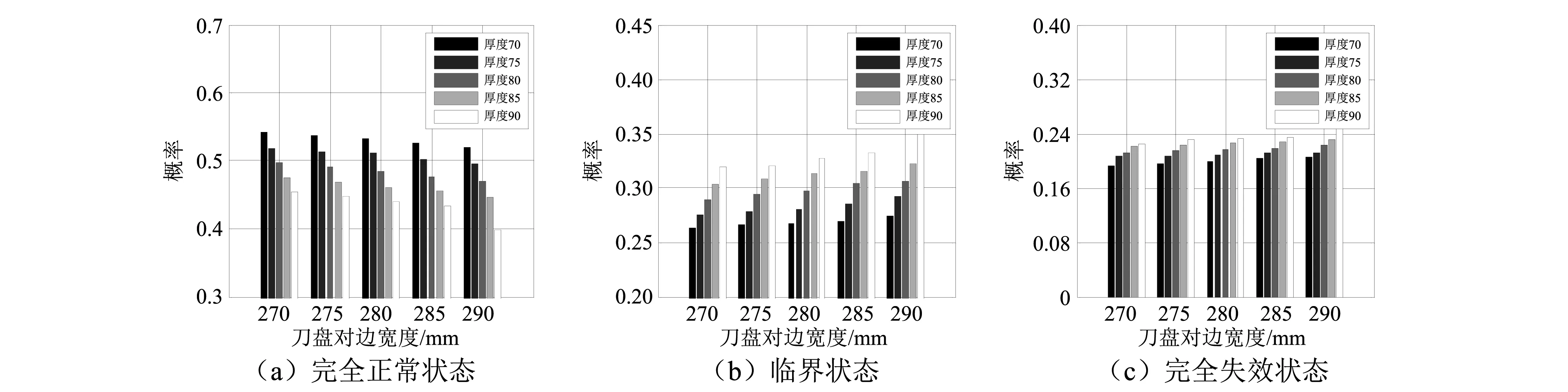
(7)判断内层试验次数q是否达到设定值M2,若q (8)直到共计M=M1×M2次随机试验全部完成,则计算得到多失效模式下系统处于状态j的概率估计值为 (3) 式中,Num(j)为计数数组的第j个元素数值。 (4) 结合概率估计值式(3),则采用Monte Carlo仿真试验方法得到系统频率可用度估计值为 (5) 1.3 相关性分析 系统频率可用度是结构随机参数向量X的函数,如何定量识别不同随机参数的变化对系统固有频率特性改变,以至频率可靠性变化的影响程度和影响方向,是对系统进行优化设计的基础。相关性分析可以用于定量两个随机变量之间的相互依赖与影响程度[12],若相关系数的绝对值相对较大,则二者相关程度较高,反之二者依赖程度较低;因此依据随机参数与系统状态的相关性系数可以评判出影响程度最大的随机参数,用于指导系统结构优化。在图4所示借助Monte Carlo仿真分析系统频率可靠性的基础上,可以同时得到随机参数设计变量Xi与系统状态g(Z)之间的相关性系数估计值为 (6) 2.1 工作原理及结构模型简化 如图5所示为刀架结构三维模型:伺服电机提供的转位动力通过三级齿轮传动系传递到主轴上,经由内端齿盘过渡,通过螺栓连接再传递到刀盘上,完成目标工位的初步定位;另一方面,右端齿盘在箱体腔内的油缸中沿轴向滑动,通过内、外、右三片式端齿盘锁紧结构,实现工位的精确定位。根据功能流模型的模块划分方法,可以将整机划分为4大块结构部件,如图5所示。 图5 刀架结构三维模型Fig.5 Three-dimensional model of turret structure 刀架固定安装在数控车床托板上,在工作工位夹持刀具参与切削加工时,端齿盘结构在油压作用下保持锁紧,以保证刀盘结构部件直接承受的切削动载荷能平稳传至箱体并导入车床床身。在承载过程中,刀架各个零部件之间均无相对运动,因此在建立刀架系统动力学模型时需要针对研究重点,将其简化为合理的分析模型。根据刀架承受切削载荷时的力传递路径,安装在箱体中的转位结构部件(即三级减速齿轮系)不承受任何方向的外载荷,因此将前两级轴系的质量(含伺服电机)作为配重加在箱体上视为箱体座整体,将第三级轴系视为主轴整体,忽略零件间连接刚度的影响;刀具安装在刀盘工作工位,将其质量累计在刀盘上,并忽略刀具与刀盘连接刚度的影响。 2.2 动力学模型搭建 系统动力学模型的搭建是分析其固有频率特性的基础。多体系统传递矩阵法(MS-TMM)是一种快捷有效的分析方法[13],其总体思路为:首先将复杂多体系统“化整为零”,分割成若干个具有通用特性的元件,如“刚体”、“弹性铰”、“梁”等;每一元件的力学特性分别用矩阵表示,并将各项综合联立成系统总传递矩阵。这种方法的主要优点在于:无需建立系统总体动力学方程,程式化程度高能灵活拼装不同结构型式的多体系统,系统矩阵阶次低且涉及的矩阵总是实矩阵。 根据刀架各个部件的自然属性,基于MS-TMM将系统划分为多个元件,分别视为空间刚体和弹性铰,建立如图6所示的多体动力学模型。根据“体”和“铰”统一编号原则,基座(机床托板)编号为0,从箱体到刀盘,各元件依次编号为1、2、…、13。其中箱体座2、外端齿盘4、右端齿盘6、主轴9、内端齿盘11、刀盘13均视为相互独立的空间振动刚体;而各振动刚体之间的结合部则采用空间弹性铰元件来表征,通过三向弹簧和三向扭簧同时描述各个方向的刚度特性:其中箱体座与基座、外端齿盘与箱体座、内端齿盘与主轴、刀盘与内端齿盘之间的螺栓联接依次编号为1、3、10、12;右端齿盘与外端齿盘、内端齿盘与右端齿盘之间的油压锁紧接触分别编号为5、7;主轴与箱体之间的轴承支承则视为空间弹性铰8。因此刀架的多体动力学模型即为:在基座支撑下,由7个空间弹性铰联接的6个刚体所组成的多刚体系统。 2.3 系统传递矩阵建立 根据MS-TMM所建立的多体系统传递矩阵库以及符号约定,定义刀架动力学模型中不同振动刚体间各个联接点的状态矢量。状态矢量是一维列阵,用于描述系统不同振动刚体之间各联接点状态的位移、转角、内力矩和内力,共计15个节点的状态矢量分别为Z0,1、Z2,1、Z2,3、Z2,8、Z4,3、Z4,5、Z6,5、Z6,7、Z11,7、Z9,8、Z9,10、Z11,10、Z11,12、Z13,12、Z13,14,形式均可表示为 Z= (7) 式中,X、Y、Z分别为惯性坐标系下位移的模态坐标,Θx、Θy、Θz分别为惯性坐标系下角位移的模态坐标,Mx、My、Mz分别为惯性坐标系下内力矩分量的模态坐标,Qx、Qy、Qz分别为惯性坐标系下内力分量的模态坐标。 根据图6所示动力学模型,由各元件传递矩阵联立得到系统矩阵形式为 Uall·Zall=O36×1 (8) 图6 刀架系统动力学模型Fig.6 Dynamic model of turret system 式中系统总传递矩阵、总状态矢量分别为 (9) (10) 刀架固定在基座0上,即Z0,1中惯性坐标系下位移、角位移的模态坐标元素均为零;刀架不参与切削加工时,刀盘不承受外载荷作用处于自由状态,即Z13,14中惯性坐标系下内力、内力矩的模态坐标元素均为零。因此,系统边界条件为 Z0,1=<0,0,0,0,0,0,Mx,My,Mz,Qx,Qy,Qz>0,1 (11) Z13,14= (12) (13) 通过求解式(13)即可计算出系统各阶固有频率ωi(i=1,2,3,…)。 3.1 结构随机参数确定 在所建立的刀架动力学模型中,零部件自身及相互之间的质量、刚度特性体现在不同类型元件的传递矩阵当中,矩阵元素中所包含的随机参数使得系统固有频率特性也具有随机性。定义刀架结构随机参数向量 X= (14) 3.1.1 空间弹性铰 空间弹性铰元件用以描述机械结构中零部件之间“结合部”的刚度特性,其理论依据来自于普遍采用的通过若干弹簧构成的动力学模型来等效结合部的动态特征。 箱体与基座、外端齿盘与箱体、内端齿盘与主轴,以及刀盘与内端齿盘均采用螺纹连接以实现不同零件之间的固连。吉村允孝研究指出当平均接触压力相同时,单位面积结合面的动态性能数据相同[14]。根据吉村允孝积分法,空间弹性铰元件1、3、10、12各个方向上的等效线性/扭转刚度随机参数均值通过分别对结合面积求积分来确定,如表1所示。 右端齿盘与外端齿盘、内端齿盘与右端齿盘之间通过油压锁紧实现零件之间齿牙彼此相嵌的啮合接触。李浦等[15]提出运用有限元方法和应变能理论,通过对等截面圆环柱体的拉伸刚度EA和抗扭刚度GIP进行修正,得到端齿连接段的轴向刚度和扭转刚度,其中圆环柱体的内外直径分别等同于端齿的内外径。采用该方法即得到空间弹性铰元件5、7各个方向等效线性/扭转刚度随机参数均值,如表1所示。 主轴与箱体之间采用深沟球轴承16009支承,轴承主要参数为钢球直径DW=12 mm,钢球中心节圆直径dm=60 mm,钢球个数Z=10,内、外圈沟道曲率半径系数分别为fi=0.515、fe=0.520,实际工作接触角α=15°。滚动轴承不承受扭矩,当径向位移δr=0.001 mm,轴向位移δa=0.005 mm,根据经验公式[16]即可计算得到空间弹簧元件8各个方向的等效线性刚度随机参数均值,如表1所示。 表1 空间弹性铰元件随机参数均值 3.1.2 空间振动刚体 空间振动刚体元件直接对应着刀架零部件,统计得到各个刚体元件的质量随机参数均值,如表2所示。 表2 空间振动刚体随机参数均值 3.2 激励随机参数确定 刀架系统在工作过程中,切削载荷为随机激励作用在刀盘上,作用位置为刀盘体输出点O。假设激励频率Y~N(μ,σ2;Yl,Yr)为服从截断正态分布的随机参数,则Y的概率密度函数[17]为 f(Y;μ,σ2,Yl,Yr)= (15) 式中,φ()、Φ()分别为标准正态分布随机变量的概率密度函数、累积分布函数,并记激励频率服从Y~N(650,416.672;0,2 500)。 因此,系统基本随机参数均值向量、协方差矩阵分别表示为 E(Z)=<μK1,…,μK12,μm2,…,μm13,μY> (16) (17) 式中,对任意空间弹性铰i有(i=1,3,5,7,8,10,12)有 (18) (19) (20) 为了更为直观说明系统状态的划分区间,以某一次随机试验为例,表3列出了0~3 000 Hz范围内的系统固有频率,以及相应的状态区间划分。 表3 系统状态对应激励频率所处子区间 表4 结构随机参数与系统状态相关性系数估计值(原系统) 基于以上分析结论,拟定采用刀盘轻量化的优化方案:刀盘是刀架企业的配件产品,具有一定的互换性要求,因此其结构尺寸的设计既要兼顾刀架配套数控车床的加工行程要求,又要与行业内基本规范相匹配。鉴于此,为了使得优化后系统频率可用度最高,以刀盘对边宽度Ch、刀盘总厚度l作为可变参数建立优化模型。刀盘体与其他零部件的连接尺寸均保持不变,可变参数Ch、l具有离散取值的约束条件。假定在任意可变参数组合下求得的刀盘体质量均服从正态分布,变异系数CV=σ/μ=0.01,因此建立单目标离散变量优化函数为 (21) 式中Function表示基于Monte Carlo仿真的系统频率可用度求解过程。 图7显示了离散寻优的分析结果,可以清晰地看出随着刀盘体质量增大,系统处于完全正常状态的概率逐渐减小,而处于临界、完全失效状态的概率呈递增趋势。在尺寸约束条件下得到的最优刀盘体对边宽度Ch=270 mm、总厚度l=70 mm,刀盘体质量均值为25.04 kg,轻量化达到30%,此时系统频率可用度估计值为 (22) 比较式(20)、(22)可知,对刀盘进行轻量化后,在多失效模式下多状态刀架系统固有频率可靠性有了明显的提升。 图7 系统状态概率随刀盘体尺寸变化Fig.7 Changes of system status probability along with the cutter body dimensions (1)本文针对传统频率可靠性分析中共振准则二分化的不足,提出了多失效模式下多状态系统频率可靠性分析方法,综合考虑结构参数以及激励频率的随机性,应用Monte Carlo仿真估计出系统频率可用度,并根据相关性分析识别各结构随机参数对系统频率可靠性的影响。 (2)基于多体系统传递矩阵法建立了刀架动力学模型,将各阶固有频率左、右邻域划分为3个子区间以定义系统3个离散状态,将本文所提出方法应用于系统不同状态的概率估计,并根据所识别出的影响最大的刀盘体质量随机参数提出优化方案,结果显示轻量化后系统频率可用度明显提升。 [1] LÜ C, ZHANG Y, WANG X, et al. Frequency reliability-based robust design of the suspension device of a jarring machine with arbitrary distribution parameters[J]. Mechanics Based Design of Structures and Machines, 2015, 43(4): 487-500. [2] 吕春梅, 张义民, 冯文周, 等. 多跨转子系统频率可靠性灵敏度与稳健设计[J]. 机械工程学报, 2012, 48(10): 178-183. LÜ Chunmei, ZHANG Yimin, FENG Wenzhou, et al. Frequency reliability sensitivity and robust design of the multispan rotor system [J]. Journal of Mechanical Engineering, 2012, 48(10): 178-183. [3] XU B, JIANG J, TONG W, et al. Topology group concept for truss topology optimization with frequency constraints[J]. Journal of Sound and Vibration, 2003, 261(5): 911-925. [4] 翟红波, 吴子燕, 刘永寿, 等. 两端简支输流管道共振可靠度分析[J]. 振动与冲击, 2012, 31(12): 160-164. ZHAI Hongbo, WU Ziyan. LIU Yongshou, et al. Analysis of resonance reliability for a simply supported pipe conveying fluid[J]. Journal of Vibration and Shock, 2012, 31(12): 160-164. [5] 黄益民, 刘伟, 刘永寿, 等. 充液管道模态的参数灵敏度及其共振可靠性分析[J].振动与冲击, 2010, 29(1): 193-195. HANG Yimin, LIU Wei, LIU Yongshou, et al. Parameter sensitivity and resonance reliability of a fluid-filled pipeline[J]. Journal of Vibration and Shock, 2010, 29(1): 193-195. [6] MENG L, LI S, LI H, et al. Frequency reliability sensitivity analysis for rotor system with random parameters[J]. Applied Mechanics and Materials, 2014, 670: 1029-1032. [7] 冯文周, 曹树谦, 赵峰, 等. 电梯系统共振失效的灵敏度研究[J].振动与冲击, 2015, 34(1): 165-170. FENG Wenzhou, CAO Shuqian, ZHAO Feng, et al. Resonance failure sensitivity for elevator system[J]. Journal of Vibration and Shock, 2015, 34(1): 165-170. [8] 辛晓辉, 曹树谦, 陈予恕. 30m2双层非线性共振筛模态计算与动态性能评价[J]. 煤炭学报, 2005, 30(2): 247-240. XIN Xiaohui, CAO Shuqian, CHEN Yushu. Modal analysis and evaluation of dynamic characteristic for the 30m2 nonlinear resonance screen with two decks[J]. Journal of China Coal Society, 2005, 30(2): 247-240. [9] ZIO E, MARELLA M, PODOFILLINI L. A Monte Carlo simulation approach to the availability assessment of multi-state systems with operational dependencies[J]. Reliability Engineering & System Safety, 2007, 92(7): 871-882. [10] LIU C, CHEN N, YANG J. New method for multi-state system reliability analysis based on linear algebraic representation[J]. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, 2015, 229(5):469-482. [11] LISNIANSKI A, LEVITIN G. Multi-state system reliability: assessment, optimization and applications[M]. Singapore: World Scientific, 2003. [12] 何斌, 芮筱亭, 贠来峰, 等. 自行火炮固有频率相关性分析的 Monte Carlo 传递矩阵法[J]. 振动与冲击, 2008, 27(11): 83-86. HE Bin, RUI Xiaoting, YUN Laifeng, et al. Monte Carlo transfer matrix method for analysis of natural frequency correlation for self-propelled artilary[J]. Journal of Vibration and Shock, 2008, 27(11): 83-86. [13] RUI X, WANG G, LU Y, et al. Transfer matrix method for linear multibody system[J]. Multibody System Dynamics, 2008, 19(3): 179-207. [14] YOSHIMURA M. Computer-aided design improvement of machine tool structure incorporating joint dynamics data[J]. Annals of the CIRP, 1979, 28(1): 241-246. [15] 李浦, 袁奇, 高进. 应变能理论在端面齿连接段刚度的应用方法研究[J]. 热力透平, 2012, 41(1): 44-48. LI Pu, YUAN Qi, GAO Jin. Study on the stiffness calculation of hirth facial serration couplings using strain energy theory[J]. Thermal Turbine, 2012, 41(1): 44-48. [16] 罗继伟, 罗天宇. 滚动轴承分析计算与应用[M]. 北京: 机械工业出版社, 2009: 90-91. [17] 池巧君, 吕震宙, 宋述芳. 截断正态分布情况下失效概率计算的截断重要抽样法[J]. 计算力学学报, 2010, 27(6): 1079-1084. CHI Qiaojun, LÜ Zhenzhou, SONG Shufang. Truncated importance sampling method for failure probability estimation with truncated normal distribution[J]. Chinese Journal of Computational Mechanics, 2010, 27(6): 1079-1084. Frequency reliability analysis on multi-state servo turret systems with multiple failure modes LIU Chenxi1, CHEN Nan2 (1. School of Mechanical Engineering, Jiangsu University, Zhenjiang 212013, China;2. School of Mechanical Engineering, Southeast University, Nanjing 211189, China) According to the continuity of frequency response function curves, the method of simply dichomizing into resonant and non-resonant zones in conventional frequency reliability analysis is debatable. A new method for multi-state frequency reliability analysis with multiple failure modes was proposed, in which, the randomness of structural parameters and excitation frequency were taken into account. The Monte Carlo simulation was applied to estimate the system frequency availability, simultaneously, in accordance with the correlation analysis, the influences of each structural random parameter were identified. The new method was applied in a servo turret system, whose dynamic model was established by the transfer matrix method for multibody systems. Then, its frequency availability and the most related structural parameter were obtained, which provides a basis for further optimization. servo turret; multiple failure modes; multi-state; frequency reliability; correlation 国家“高档数控机床与基础制造装备”科技重大专项(2012ZX04002-032;2013ZX04012-032) 2016-02-17 修改稿收到日期: 2016-06-03 刘晨曦 女,博士,1988年生 陈南 男,教授,博士生导师,1953年生 TG659;TH113.1 A 10.13465/j.cnki.jvs.2017.14.012


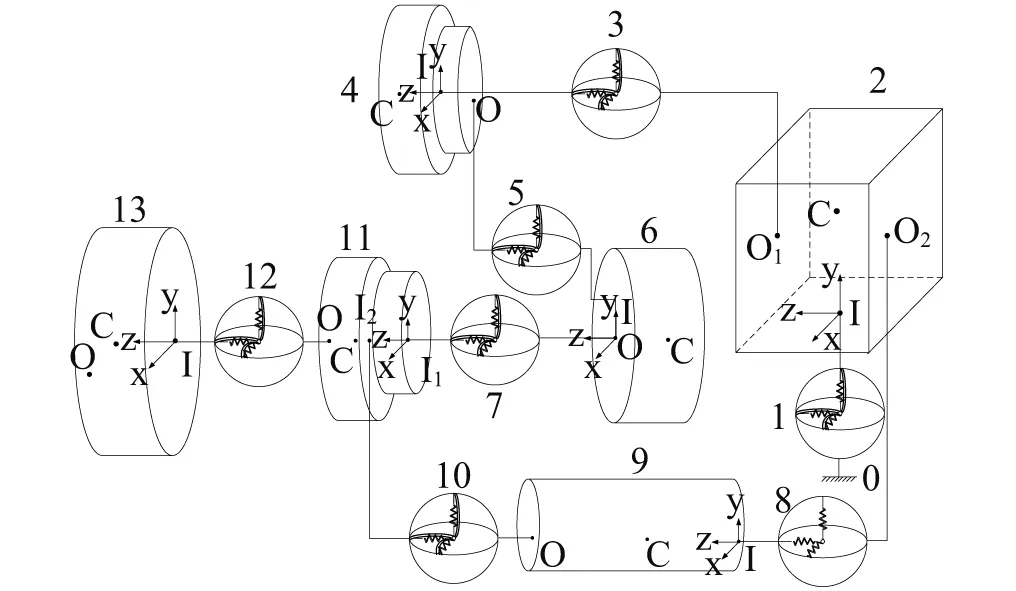
2 刀架系统动力学模型

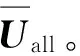
3 基本随机参数向量
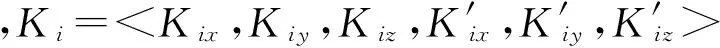


4 系统频率可靠性分析

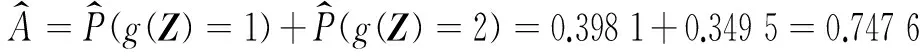




5 结 论
