基于正交试验的 TBM 双板刀盘结构参数优化设计
2022-10-20张照煌杨远圣程克凤
张照煌,杨远圣,程克凤
华北电力大学能源动力与机械工程学院 北京 102206
全 断面岩石掘进机 (Full Face Rock Tunnel Boring Machine,TBM) 是岩石质隧道 (洞) 全断面施工的大型机械设备,广泛用于城市地铁、铁路公路隧道、水利水电隧洞等工程施工[1]。第一台全断面岩石掘进机于 20 世纪 50 年代由美国罗宾斯公司研制,刀盘为单板结构,后续研究人员为了提高 TBM 掘进效率与地质适应性,将单板刀盘改进为双板刀盘和三板刀盘。基于减少换刀人员的工作量和提高安全性,安装在刀盘上的盘形滚刀也从凸置安装演变为凹置安装[2]。刀盘是 TBM 的核心部件,位于 TBM 最前端,具有直接向盘形滚刀施加破岩力、稳定掘进面等功能,其刚度直接影响 TBM 掘进系统功能的发挥。地质条件的复杂性和作业环境对 TBM 刀盘结构刚度提出了严苛要求。刀盘结构设计对提高 TBM 盘形滚刀破岩能力和掘进效率,降低掘进成本具有显著作用,是影响 TBM 掘进性能的决定因素[3]。因此,刀盘结构设计一直是 TBM 领域研究的重要关键问题之一。
就刀盘纵向 (垂直于刀盘面的方向) 形变而言,刀盘结构设计的基本载荷是破岩盘形滚刀作用在刀盘上的力及与之相平衡的刀盘大轴承的推进力。根据盘形滚刀的压痕试验和线性滚压破碎岩石的试验,国内外学者提出并建立了多套盘形滚刀受力预测模型,典型模型如美国科罗拉多矿业学院 CSM 模型[4]、罗克斯巴勒预测公式[5]、伊万斯预测公式[6]等。笔者项目团队根据压痕试验建立了盘形滚刀破岩垂直力计算公式[7],并根据对刀盘形变的理论研究,先后提出并建立了全断面岩石掘进机刀盘支撑刚度理论[8]、刀盘形变理论[9]、刀盘面板弯曲理论[10]以及刀盘弯曲模型理论[11]等。李坚等对刀盘外部载荷的确定[12]进行了研究。刀盘所受载荷随机性强,因此,刀盘的振动多表现为受迫弹性体的扭转振动和横向振动[13]。刀盘振动对盘形滚刀、刀盘、刀盘大轴承等的寿命及 TBM 掘进性能都有重大影响。因此,合理的刀盘结构参数确定理论及相应设计是实现 TBM 刀盘性能的关键。基于此,笔者以 TBM 双板刀盘为研究对象,以刀盘前板厚度、后板厚度、前后板间距、刀盘支撑半径与刀盘半径之比 (撑盘径比) 等双板刀盘结构参数为自变量,通过正交试验和有限元仿真分析,研究双板刀盘结构参数与刀盘形变间的关系。
1 双板刀盘结构与正交试验设计
1.1 双板刀盘结构
初期的 TBM 刀盘基本为单板结构,即刀盘体可以认为是一块均匀的钢板。随着科学技术和 TBM 施工实践的发展,为提高 TBM 对施工地质岩石的适应性,TBM 刀盘逐渐从单板发展为双板箱型结构[2],如图 1 所示。
起初的双板箱型结构刀盘基本保留着单板刀盘的外形,最典型的结构就是凸置的盘形滚刀座。在 TBM掘进过程中,凸置式盘形滚刀座不仅容易磨损,还容易被剥落的岩石砸坏,同时不方便技术人员通过人孔进入刀盘前面换刀。因此,凸置式刀座逐渐被淘汰,产生了凹置式 (背装式) 盘形滚刀座,如图 2 所示,实现了 TBM 盘形滚刀的刀盘后检修与更换。
1.2 正交试验设计
根据 TBM 刀盘双板结构特点,设置前板厚度δ1、后板厚度δ2、板间距t、撑盘径比R0/R(R0为刀盘大轴承半径,R为刀盘半径) 4个参数 (因素)为自变量,进行刀盘形变的研究。若要得到形变最优的双板结构刀盘,就需要δ1、δ2、t、R0/R的最佳组合。若每个因素赋予 5个水平 (取值),为了包含所有水平就需要进行 54=625 次试验。显然如此多的试验次数会耗费相当大的人力和物力,即便采用数字模拟,也会耗费相当长的时间。
正交试验设计是研究多因素多水平的一种高效、快速、经济的设计方法[14]。按正交试验设计,只需进行 5×5=25 次试验就可实现预期目标,大大减少了工作量。根据双板箱型结构刀盘的相关资料,选取一定范围内的刀盘结构参数,给出相应的刀盘因素水平,如表 1 所列。
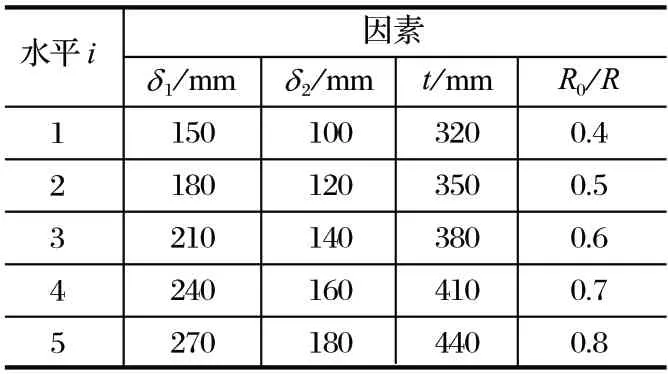
表1 刀盘因素水平Tab.1 Cutterhead factor level table
通过正交试验设计,25 组双板刀盘仿真试验方案如表 2 所列。
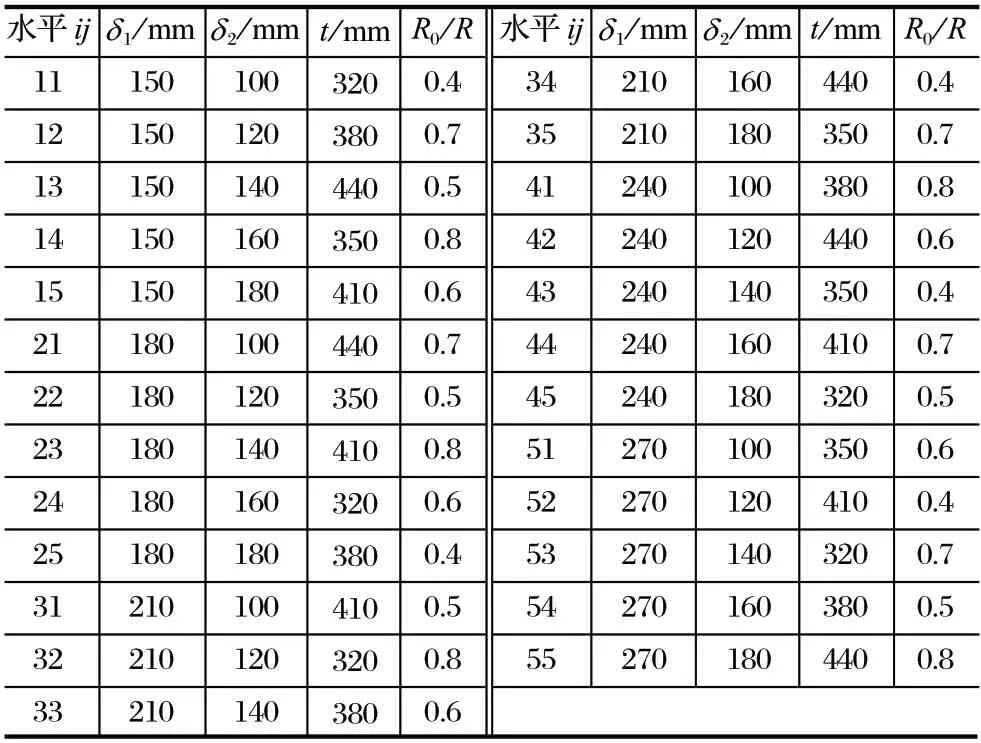
表2 双板刀盘仿真试验方案Tab.2 Scheme of simulation test for double-plate cutterhead
2 刀盘仿真与数据分析
2.1 建模与初始条件设定
以某隧洞工程施工用 TBM 刀盘为研究对象。该TBM 刀盘直径为 8 m,共布置 51 把盘形滚刀,其中有 8 把中心刀、39 把正刀、4 把边滚刀及 4个人孔。为方便有限元分析,删除刀盘多余结构,如铲斗、喷水孔等。刀盘前后板通过滚刀座连接。建立该刀盘的SolidWorks 模型并导入 ANSYS,如图 3 所示。
双板刀盘网格划分为四面体网格,材料参数如表3 所列。

表3 双板刀盘材料Tab.3 Material of double-plate cutterhead
TBM 掘进作业时,刀盘推力和转矩通过盘形滚刀传递给岩石。因此,在盘形滚刀实际破岩过程中,盘形滚刀将受到垂直力 (法向力)、滚动力 (切向力)、侧向力以及惯性力等岩石反作用力,如图 4 所示。相对于盘形滚刀的法向力,其他力的数值相对较小,如盘形滚刀的切向力和侧向力一般约为其法向力的 0.10~ 0.15 倍,因此,刀盘弹性变形只考虑盘形滚刀法向力的作用[15],即对刀盘形变影响较大的、起主要作用的载荷是作用在其上的盘形滚刀的垂直力。因此,TBM 掘进作业过程中,刀盘的形变主要是指垂直于未变形 (没受载荷) 刀盘面的形变,即刀盘的纵向形变(挠度)。
该工程采用的是 19 英寸盘形滚刀,其额定载荷为 260 kN。TBM 掘进作业过程中,盘形滚刀所受到的破岩力通过盘形滚刀座传递给刀盘,所以在仿真过程中,对每把盘形滚刀安装座施加盘形滚刀破岩额定法向力[16],其值为 260 kN。
2.2 仿真数据分析
根据 TBM 刀盘初始条件和给定的正交试验设计方案,采用 ANSYS 软件进行仿真计算,分别提取 25组方案的刀盘半径上不同考察点的变形平均值wijr,计算出变形均方差σij(刀盘形变均匀性评价指标),如表 4 所列。
为形象对比各方案刀盘的挠度变化,将刀盘半径上的形变平均值用坐标图表示 (每 5个刀盘方案绘制在同一图上),如图 5 所示。
从表 4 均方差和图 5 各刀盘方案变形曲线的平缓程度可以看出,双板刀盘正交试验方案 45 (对应刀盘前板厚 240 mm、后板厚180 mm、两板间距 320mm、撑径比 0.5) 和 54 (对应刀盘前板厚 270 mm、后板厚 160 mm、两板间距 380 mm、撑径比 0.5) 的刀盘形变相对较均匀 (变形量均方差在最小量级上),即刀盘整体具有较好刚度。从图 5 中还可以看出,双板刀盘在集中载荷作用下,不管刀盘结构参数如何变化,刀盘变形最大位置一直位于刀盘中心或边缘。

表4 刀盘各方案的挠度Tab.4 Deflection of each cutterhead scheme m
3 指标参数及其极差分析
通过 ANSYS 仿真计算,得出了正交试验的 25组刀盘方案的形变均方差值,并得到了刀盘形变较均匀方案。为分析前板厚度、后板厚度、两板间距、撑径比等参数对刀盘形变的影响程度,根据正交试验,定义指标参数ki,其中,刀盘前板厚度、后板厚度、两板间距、撑径比等的指标参数分别记为和且
定义指标参数极差 ΔK,其中,刀盘前板厚度、后板厚度、两板间距、撑径比等的指标参数极差分别记为 ΔKδ1、ΔKδ2、ΔKt、ΔKR0/R,且
将表 4 中的σij分别代入式 (1)~ (4) 进行计算,将计算结果代入式 (5),再将相应数据列表,如表 5所列 (为方便表达,将指标参数和指标参数极差右上标移入表 5 第 1 行)。
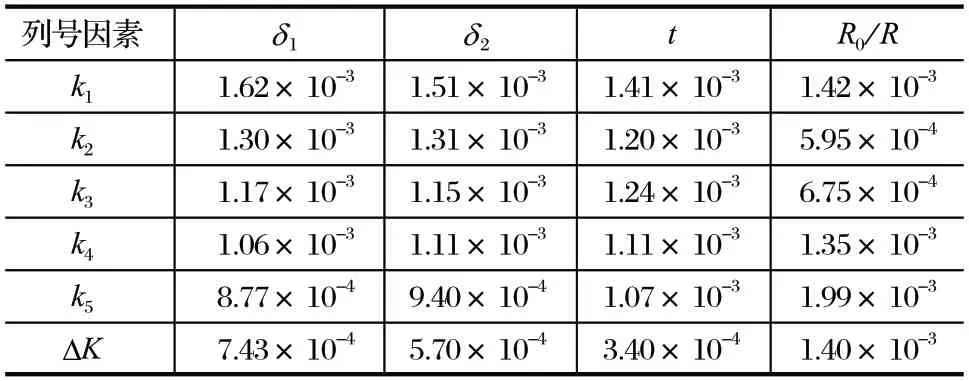
表5 刀盘形变极差分析Tab.5 Range analysis of cutterhead deformation m
由式 (1)~ (4) 可以看出,ki为刀盘某参数单一水平不变,其他参数水平变化的刀盘各点平均变形量的均方差之和,也称指标和。极差 ΔK反映了某因素对刀盘形变均匀性的影响程度。
由表 5 可以看出
其所对应的刀盘结构参数分别为前板厚度为 270 mm,后板厚度为 180 mm,板间距为 440 mm,刀盘大轴承半径与刀盘半径比为 0.5。对此方案的刀盘进行有限元分析,其变形量均方差为 6.63× 10-5,小于 45、54参数组合方案刀盘变形量均方差,因此,实际最优双板刀盘结构参数应为前板厚度取 270 mm,后板厚度取 180 mm,板间距取 440 mm,刀盘大轴承半径与刀盘半径比取 0.5。
由表 5 还可以看出,ΔKR0/R>ΔKδ1>ΔKδ2>ΔKt。因此,刀盘大轴承半径与刀盘半径比和刀盘前板厚度是影响刀盘形变的主要因素,刀盘后板厚度和板间距是影响刀盘形变的次要因素;所研究因素对刀盘变形影响的水平顺序是第 4 水平为板间距,第 3 水平为后板厚度,第 2 水平为前板厚度,第 1 水平为刀盘大轴承半径与刀盘半径比。
4 结论
(1) 双板刀盘在集中载荷作用下,不管其结构参数如何组合变化,刀盘变形最大位置一直位于刀盘中心或边缘。
(2) 在本研究的参数范围内,双板刀盘结构,刀盘形变较均匀的结构参数组合为前板厚度取 270 mm,后板厚度取 180 mm,板间距取 440 mm,刀盘大轴承半径与刀盘半径比取 0.5。
(3) 影响双板刀盘形变均匀性的因素水平依次是第 4 水平为板间距,第 3 水平为后板厚度,第 2 水平为前板厚度,第 1 水平为刀盘大轴承半径与刀盘半径之比。
