带锥斗筒仓中稻谷的密度与应力分布模型

杜小翠 严晓婕 程绪铎 高梦瑶 冯家畅

(南京财经大学食品科学与工程学院；江苏省现代粮食流通与安全协同创新中心，南京 210046)

带锥斗筒仓中稻谷的密度与应力分布模型

杜小翠 严晓婕 程绪铎 高梦瑶 冯家畅

(南京财经大学食品科学与工程学院；江苏省现代粮食流通与安全协同创新中心，南京 210046)

采用LHT-1粮食回弹模量仪测定稻谷堆的压缩密度，建立带锥斗筒仓中稻谷堆的密度、应力与粮层深度关系的微分方程组，用数值方法计算带锥斗筒仓中稻谷密度、应力与粮层深度关系，由积分法计算出筒仓中稻谷的储藏总质量。试验结果表明，淮稻5号(含水率为10.38%～18.30% w.b.)的密度随竖直应力(0.495～245.892 kPa)增大而增大(582.772～696.593 kg/m3)。模型计算结果表明，在带锥斗筒仓的筒体部分，稻谷堆密度随着粮层深度的增加而增大；到锥斗部分，稻谷堆密度随着粮层深度的增加而逐渐减小。在带锥斗筒仓的筒体部分，稻谷堆的竖直应力随着粮层深度的增加而增大；在锥斗部分，稻谷堆的竖直应力则随着粮层深度的增加而减小。在带锥斗筒仓中的筒体部分，稻谷堆的侧向应力随着粮层深度的增大而增大；在筒体与锥斗结合处，稻谷堆的侧向应力突然增加；到了锥斗部分，稻谷堆的侧向应力随着粮层深度的增大先稍增大再逐渐减小。

带锥斗筒仓 稻谷 密度 竖直应力 侧向应力

稻谷是我国单产最高、总产最多的粮食作物，在国民经济和国家粮食安全中具有重要的地位和作用[1]。筒仓是储粮仓型中机械化程度最高的一种仓型，被广泛应用于稻谷的储藏[2-3]。稻谷储藏在筒仓中，会受到自重、内摩擦力以及仓壁的支持力，稻谷堆的内部由于这些力的作用产生应力，从而产生弹性和塑性形变，稻谷堆的体积缩小，密度则增大，随着粮层深度的增加，稻谷的密度增大[4-5]。准确地计算出筒仓中密度的分布就能准确的计算筒仓中稻谷的总质量。目前我国粮食储藏质量检查方法是体积密度法[6]。体积密度法是将稻谷堆的体积与平均密度相乘来计算稻谷质量，稻谷堆的平均密度为常规测定的密度乘以修正系数，修正系数是凭经验给出的，这个方法计算的粮仓中稻谷质量误差大。储藏在筒仓中的稻谷压应力随着粮层深度的增加而增大。筒仓中稻谷堆的压应力随粮层深度的分布值是粮仓结构设计所需要的重要参数。

Mahmoud[7]使用一个非线性双曲线型本构方程，建立了有限元模型，估算了由弹性波纹板构成的圆筒仓仓壁静态压力。Zhang等[8]利用Lade模型计算了粮仓的静态仓壁压力，并研究了温度对仓壁侧压力的影响。Ruckenbrod等[9]和Ragneau等[10]使用不同的物料本构方程通过有限元方法估算了圆筒仓中物料的静态压力和卸料动压力。Goode等[11]通过有限元方法估算了薄壁矩形截面筒仓的内小麦的静压力。上述对筒仓中物料压应力的研究都是将物料密度视为常量，没有考虑密度的变化对应力分布的影响。Loewer等[12]观测了小麦的堆密度随压力和水分的变化值。Thompson 等[13]试验测定了小麦的堆密度随压力和水分的变化值并给出了预测密度的经验方程。Moya等[14]使用固结仪测定几种谷物的孔隙率与密度与竖直压力的关系。这些研究只是在小容器中测定密度与压力的关系。陈德民等[15]利用压力传感器网络进行粮食储藏质量在线监测，给出了压力传感器外围电路的硬件设计，并根据我国粮仓特点对传感器进行了布置，利用VC++6.0开发了系统管理软件。在筒壁和底部安装力传感器，由仓底与仓壁的压力分布推出粮仓储粮总质量，这个方法本质上是由仓壁与仓底压力分布估算平均密度，再算出总质量。这个方法测算的误差大、成本大，难以推广。到目前为止，筒仓中粮堆的密度分布和装粮质量的理论研究成果鲜见报导，也鲜有有效的测量方法。

本试验采用LHT-1粮食回弹模量仪来测定稻谷堆在不同压应力下的压缩密度，用试验数据拟合压缩密度与压应力的关系模型，建立筒仓中稻谷堆的密度、压应力与粮层深度关系的微分方程组，用数值方法计算得到筒仓中稻谷密度随粮层深度变化关系，从而由积分法计算出筒仓中稻谷的储藏总质量。同时，用数值方法计算得到筒仓中随粮层深度变化的稻谷堆的竖直应力、侧向应力的分布值。

1 稻谷堆密度与最大主应力关系的试验测定

稻谷储藏在筒仓的圆筒中，处于主动应力状态，最大主应力是竖直方向；稻谷储藏在筒仓的锥斗中，处于被动应力状态，最大主应力垂直锥斗壁。密度与最大主应力的关系(ρ=F(pmix))通过试验来确定。

1.1 材料与方法

1.1.1 试验材料

淮稻5号稻谷，原始水分为15.23%(湿基)，2014年产于江苏淮安。2014年11至12月进行压缩试验。

试验时，将其水分调节为10.38%、12.38%、13.77%、15.23%、16.99%、18.30% w.b.。稻谷籽粒的最大直径、中直径、最小直径的平均值分别为7.5、3.6、2.4 mm，对应的标准差分别为0.2、0.1、0.1 mm。(随机取样100粒稻谷粒，用游标卡尺测得其3个粒径，精确到0.1 mm，最后求其平均值)

1.1.2 试验仪器

LHT-1型粮食回弹模量测定仪：南京土壤仪器厂有限公司；HG202-2(2A/2AD)电热干燥箱：南京盈鑫实验仪器有限公司；AL204型分析天平、JSFD-粉碎机：上海嘉定粮油仪器有限公司。

1.1.3 试验原理

将稻谷装入LHT-1粮食回弹模量仪的圆筒中，顶部加载荷，圆筒中的稻谷处于主动应力状态，稻谷在圆筒中产生限侧变形压缩[16]，这种应力状态与变形状态与筒仓中的稻谷应力状态与变形状态相似。因此，可通过对回弹模量仪的圆筒中的粮堆施加不同的顶部压力来模拟筒仓中不同深度的稻谷的应力状态与应变状态。筒壁对稻谷产生向上的摩擦力，装样筒内各粮层所受到的竖直应力与侧向应力是不同的，粮层深度增加，竖直应力与侧向应力减小。所以，本节用圆筒中稻谷的平均竖直应力与侧向应力表示筒仓中某一粮层的竖直应力与侧向应力。

采用微元法对装样筒内粮堆样品进行受力分析，假设装样筒内半径为Rc，样品高度为Hc，取距离粮面深度为y，高度为dy的微元体进行受力分析[5]，微元体在竖直方向的受力分析见图1：

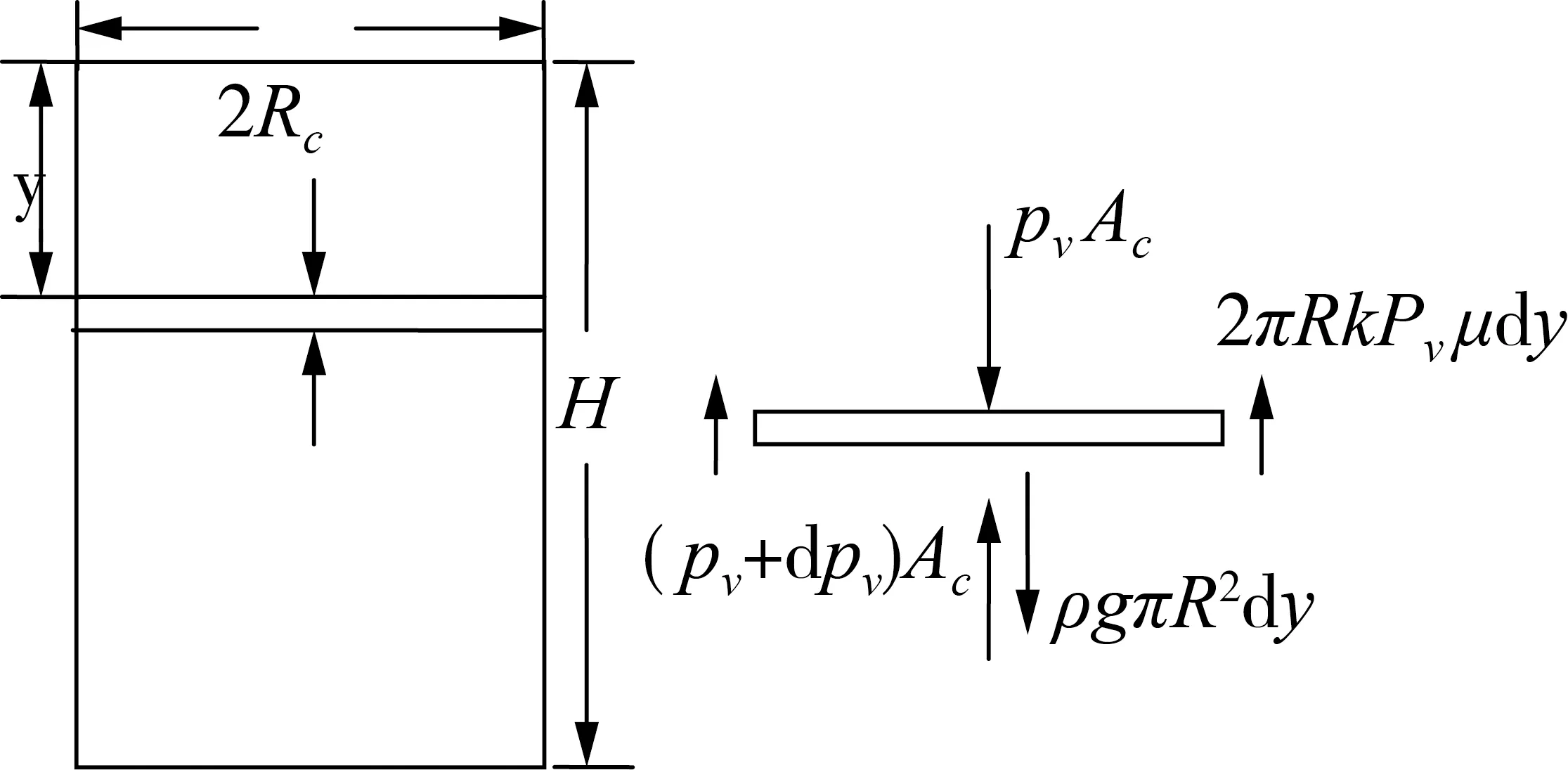
图1 回弹模量仪装样筒中粮堆微元层受力图

稻谷在装样筒内受压时处于主动应力状态，根据Rankine理论[17]和Janssen理论[18]，侧向应力与竖直应力的比为：

(1)

式中：ph1为圆筒中粮堆所受侧向应力/kPa；pv1为圆筒中粮堆所受竖直应力/kPa；φ为稻谷内摩擦角/°。

粮堆微元体在竖直方向上受力平衡，可得平衡方程为：

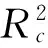
(2)

式中：ρ为稻谷密度/kg/m3；μc为稻谷与装样筒筒壁的摩擦系数；Ac为装样筒的横截面积/m2。

由式(2)，结合式(1)推导出下面的微分方程：

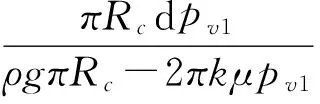
(3)

对式(3)进行积分，得：

(4)

(5)

式中：p0为粮堆顶部压应力/kPa；Hc为压缩后圆筒中粮堆高度/m。

在装入稻谷的圆筒顶部逐级加载，测定每次加载后稻谷样品的高度，计算出对应的稻谷密度，并根据式(5)计算出对应的竖直应力，即可得到稻谷样品密度与其所受竖直应力(最大主应力)的关系：

ρ=F(pmax)

(6)

1.1.4 试验方法

将回弹模量仪放在实验室中，室内温度设置为20 ℃。将样品匀速倒入装样筒中，并将其表面铺平，放上传压板，保证传压板上表面与装样筒上端齐平。保持横梁杠杆垂直，转动平衡锤调整杠杆至水平以上，用M16螺母固定平衡锤。旋转传压螺钉与传压板接触，调整0～30 mm位移传感器的触头位置，调零百分表。根据试验要求，对试样进行加载。随着试样的下沉，杠杆向下倾斜，为防止杠杆倾斜影响加载精度，调节调平手轮，使杠杆处于水平位置。试验进行3 d后记录样品高度，计算样品压缩后的体积，结束试验，倒出装样筒内的稻谷样品，称重并记录稻谷质量。稻谷堆的密度即为稻谷的质量除以压缩后的体积[5]。

1.2 结果与分析

1.2.1 平均竖直应力

淮稻5号稻谷的内摩擦角和摩擦系数随含水率的变化不显著，不同压应力条件下内摩擦角和摩擦系数不同。由直剪仪测得的试验结果见表1。

使用回弹模量仪通过逐级加载的方式对稻谷堆进行压缩试验，加载的顶部竖直应力分别为50、100、150、200、250、300 kPa。根据表1 中的参数与试验测定的样品压缩的顶部压力与样品高度，根据式(5)计算得到稻谷堆所受的平均竖直应力，结果见表2。

表1 不同压应力下稻谷的内摩擦角和摩擦系数

1.2.2 稻谷堆的压缩密度

不同含水率、不同顶部压应力下的稻谷堆压缩后测定的密度见表3。

1.2.3 稻谷堆压缩密度与平均竖直应力的关系

根据表2和表3作图，可以得到稻谷堆压缩密度与平均竖直应力的关系曲线，如图2所示。

图2 不同含水率下的稻谷堆密度与平均竖直应力的关系曲线

由图2可以得到，在同一含水率下，随着平均竖直应力的增大，稻谷堆的压缩密度增大。根据图2可拟合出稻谷堆密度与平均竖直应力的关系方程为ρ=-apv2+bpv+c(ρ=F(pmax))，其中方程系数a、b、c随含水率的变化而变化，结果见表4。

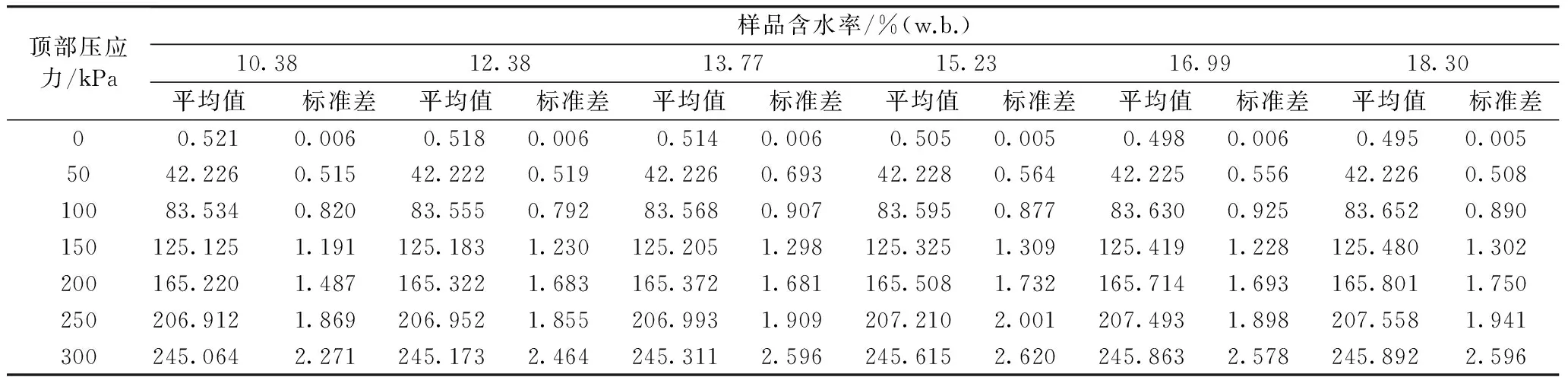
表2 不同含水率、不同顶部压力下的稻谷堆所受的平均竖直应力/kPa

表3 不同含水率、不同顶部压力下的稻谷堆的压缩密度/kg/m3

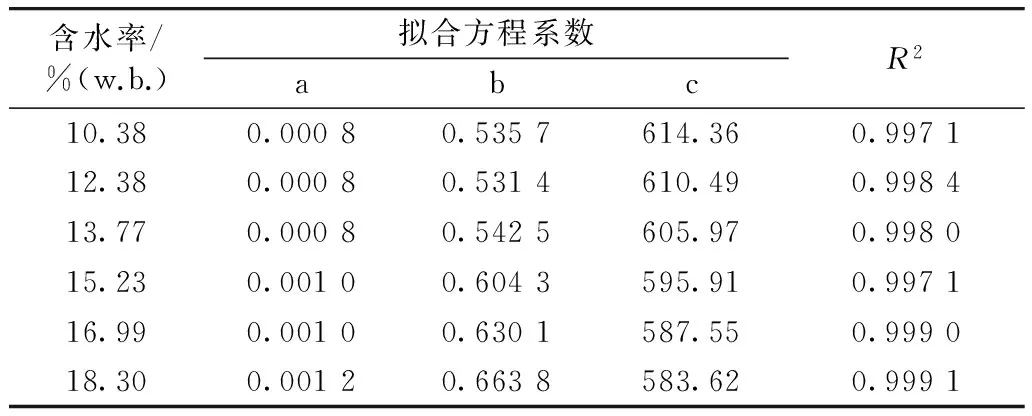
表4 平均竖直应力与稻谷堆密度的拟合方程系数

2 带锥斗筒仓内稻谷密度、压应力与粮层深度关系的微分方程组

设带锥斗筒仓的直径为D，圆筒高为H，锥斗高为h，锥斗壁与水平面夹角为α，稻谷的内摩擦角为φ，稻谷储藏在仓中，仓墙与稻谷间的摩擦系数为μ，设水平压应力与竖直应力大小不随半径的大小和方向而变化。带锥斗的筒仓和稻谷表面下深度y处稻谷的微元层受力示意图如图3所示。

对于筒仓的筒体部分，其微元层的受力如图3b所示。由于微元层在竖直方向上合力为零，则得到：

(pv+dpv)A+μphCdy-pvA-ρgAdy=0

(7)

式中：pv为稻谷竖直应力/kPa；ph为侧应压力/kPa；ρ为稻谷的密度/kg/m3；g为重力加速度/m/s-2；A为圆筒的横截面面积/m2；C为圆筒的周长/m；且

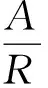
(8)

式中：R为水力半径/m；R=D/4。

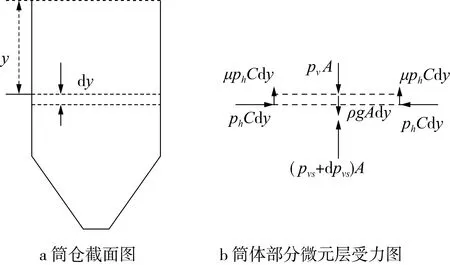
图3 筒仓的筒体中微元体受力图

稻谷静态储藏在筒仓中，稻谷处于主动应力状态，根据Janssen理论[18]，稻谷最小主应力(即筒壁侧压力ph)和最大主应力(即竖直应力pv)之比k为：

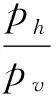
(9)

结合式(6)～式(8)得到筒体部分最大主应力pv的微分方程：

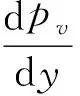
(10)

而筒体部分最小主应力ph为：

ph=kpv

(11)

对于筒仓的锥斗部分，其截面图和微元层受力如图4所示。在同一水平面上的锥斗部分微元层，其粮堆的最大主应力的大小与方向都是变化的。在锥斗壁处稻谷处于被动应力状态，此处最大主应力方向垂直于锥斗壁。筒体底层中心的最大主应力与锥斗顶面中心最大主应力是相等的。锥斗内的任一水平微元层，中心竖直应力(pvc)是该处的最大主应力，边缘竖直应力并不是该处的最大主应力，也不是该处的最小主应力，在锥斗壁处(微元层边缘处)取一微元体如图4b、图4c 所示，微元体受到的最大和最小压应力分别为phmax和phmin，phmax为锥斗壁侧压力，且微元体的最小压应力和最大压应力之比为k。

图4 筒仓锥斗部分微元体受力图

根据Rankine压力理论[22]得到水平稻谷薄层边缘处竖直应力pve：

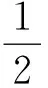
(12)

令

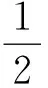
(13)

同一水平微元层的竖直应力取平均值phv：

phv=(pve+pvc)/2=(λ+1)phmax/2

(14)

作用于微元层上竖直方向的合力等于0：

phvAa+ρgV-(phv+dphv)Ab-phmaxScosα=0

(15)

式中：Aa为上底面的面积/m-2；Ab为下底面的面积/m-2；S为侧表面积/m-2；V为微元体的体积/m-2。

设水平面上稻谷薄层的半径为r，则：

Aa=πr2

(16)

Ab=π(r-dycotα)2=π(r2-2rcotαdy)

(17)

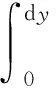
(18)

(19)

结合式(13)～式(18)式并化简得到锥斗部分最大主应力(锥斗壁侧压应力)方程：

(20)

结合式(10)、式(11)、式(6)得到筒体部分压应力、密度与粮层深度关系的方程组：

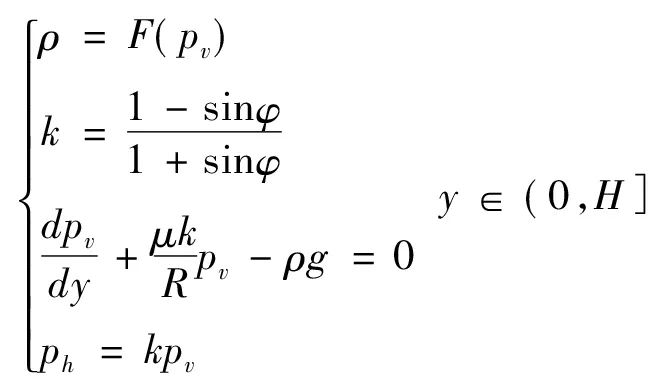
(21)

结合式(13)、式(14)、式(20)、式(6)得到锥斗部分压应力、密度与粮层深度关系的方程组：

y∈(H,H+h]

(22)

式中：phv为锥斗中粮堆竖直应力/kPa；phmax为锥斗壁侧压应力/kPa。

方程组(21)、方程组(22)的连续条件为：

pv(H)=phmax(H)

(23)

方程组(21)、方程组(22)的边界条件为：

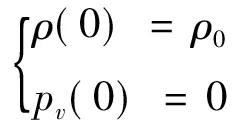
(24)

3 带锥斗筒仓中稻谷堆密度、压应力与粮层深度的关系

3.1 淮稻5号稻谷在带锥斗筒仓中的密度与粮层深度的关系

设筒仓的参数条件如表5所示。储藏稻谷的含水率为12.0% w.b.，其内摩擦角为40°，与仓壁的摩擦系数为0.35，稻谷的表面密度为600 kg/m3。稻谷堆顶部粮面是水平，并选择粮堆的每一薄层为0.1 m。数值法求解微分方程组(21)和方程组(22)，从而计算得到不同粮层深度下稻谷堆的密度，如图5所示。

表5 筒仓的参数

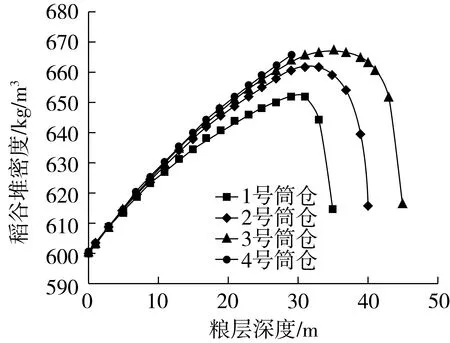
图5 稻谷堆密度与粮层深度的关系

从图5可以看出：1)1号、2号、3号筒仓中，在筒体部分，随着粮层深度的增加，稻谷堆密度先快速增大，然后再慢缓增大；到锥斗部分时，随着粮层深度的增加，稻谷堆密度开始逐渐减小。4号浅圆仓由于仓底没有带锥斗，其稻谷堆密度一直随粮层深度的增加而增大。2)在同样的粮层深度下，仓内稻谷堆的密度随着筒仓半径的增大而增大。

3.2 带锥斗筒仓中粮堆竖直应力、侧向应力与粮层深度的关系

筒仓的仓型、大小见表5，稻谷堆的其他参数同3.1。数值计算可得到不同粮层深度下稻谷堆的竖直应力与侧向应力。

3.2.1 竖直应力与粮层深度的关系

计算方程组(21)和方程组(22)给出筒仓中粮堆的竖直应力与粮层深度的关系如图6 所示。

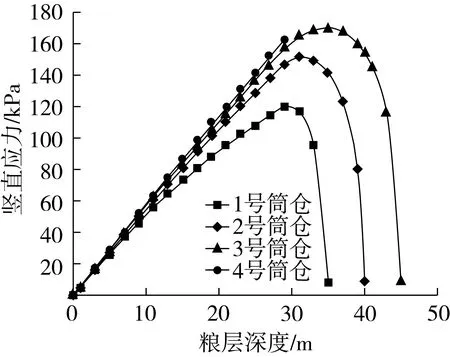
图6 稻谷堆所受竖直应力与粮层深度的关系

从图6可以看出：1)在筒体部分(1、2、3号筒仓)，稻谷堆的竖直应力都随粮层深度的增加而增大，到锥斗部分(1、2、3号筒仓)时，稻谷堆竖直应力随粮层深度的增加而减小；4号浅圆仓底部没有锥斗，稻谷堆的竖直应力一直随着粮层深度的增加而增大。2)在同样的粮层深度下，仓内稻谷堆的竖直应力随着筒仓半径的增大而增大。

3.2.2 侧向应力与粮层深度的关系

计算方程组(21)和方程组(22)给出的筒仓中粮堆的侧向应力与粮层深度的关系如图7 所示。

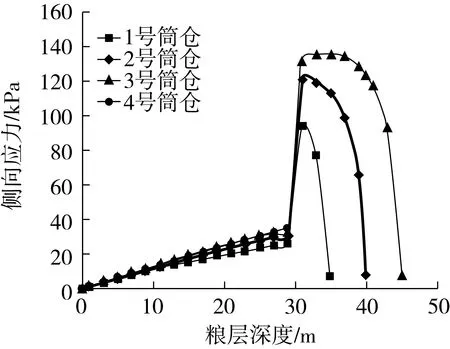
图7 稻谷堆所受侧向应力与粮层深度的关系

从图7可以看出：1)在筒体部分(1、2、3号带锥斗筒仓中)的稻谷堆的侧向应力随着粮层深度的增加而增大；在筒体与锥斗结合处，稻谷堆的侧向应力突然增加；到了锥斗部分，随着粮层深度的增加，稻谷堆所受侧向应力先稍增大再逐渐减小。4号浅圆仓底部没有锥斗，所以稻谷堆的侧向应力一直随着粮层深度的增加而增大。2)在同样的粮层深度下，稻谷堆的侧向应力随着筒仓半径的增大而增大。

4 基于密度变化机理的筒仓中稻谷储藏总质量

4.1 稻谷储藏总质量积分模型

给定筒仓及稻谷堆的各参数值，采用本模型计算出带锥斗筒仓中各粮层的密度，稻谷总质量的积分计算为式(25)。

(25)

式中，ρ1为筒体部分粮层深度y处稻谷密度/kg/m3；S1为筒体部分粮层深度y处横截面积/m2；ρ2为锥斗部分粮层深度y处稻谷密度/kg/m3；S2为锥斗部分粮层深度y处横截面积/m2。

4.2 模型预测结果

国家粮食局科学研究院小汤山试验基地1、3、5、7号筒仓内径为3 m，高度为10 m，仓内储藏粮种为稻谷。筒仓与稻谷的参数及实际账面稻谷总质量见表6。运用式(25)计算得到各个筒仓中储藏的稻谷总质量，计算结果见表6。

表6 圆仓与稻谷的参数值及模型预测的筒仓中稻谷总质量

从表6可看出，模型预测的筒仓中稻谷总质量与实际账面值几乎一致，最大误差只有0.55%。

5 模型预测与体积密度法计算结果比较

选定表6的参数，本模型计算得到的4个筒仓中稻谷总质量与常用的体积密度法计算得到的4个筒仓中稻谷总质量见表7。

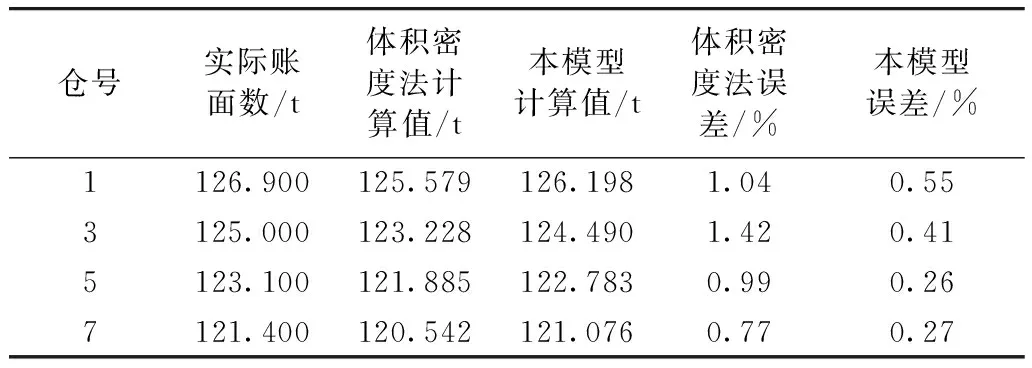
表7 本模型、常用的体积密度法得到的稻谷储藏总质量与实际账面数的比较

注：体积密度法的密度修正系数为1.015。

由表7可以看出，1、3、5、7号仓中，本模型计算得到的储藏总质量比常用的体积密度法误差小，且更接近实际账面数，体现出了本模型的可靠性。

6 结论

6.1 本试验模型预测给出：在筒仓的筒体部分，稻谷堆密度随着粮层深度的增加而增大，在锥斗部分，随着粮层深度的增加而减小。由本模型预测的密度而计算得到的国家粮食局科学研究院小汤山试验基地1、3、5、7号筒仓稻谷储藏总质量与实际账面数的误差为0.38，常用的体积密度法计算值与实际账面数的误差为1.06，这体现出了本模型的可靠性。

6.2 本试验模型预测给出：在筒仓的筒体部分，稻谷堆竖直应力随粮层深度的增加而减小；在锥斗部分，稻谷堆竖直应力随着粮层深度的增加而减小。

6.3 本试验模型预测给出：在筒仓的筒体部分，稻谷堆侧向应力随着粮层深度的增加而增大；在筒体与锥斗结合处，稻谷堆侧向应力突然增加；到了锥斗部分，随着粮层深度的增加，稻谷堆侧向应力先稍增大再逐渐减小。

[1]王瑞元，朱永义，谢健，等.我国稻谷加工业现状与展望[J].粮食与饲料工业，2011(3)：1-5 Wang R Y，Zhu Y Y，Xie J，et al.Present situation and prospect of rice processing industry in China[J].Cereal and Feed Industry，2011(3)：1-5

[2]张承光.现代化储粮仓型的选择[J].粮油仓储科技通讯，2002(2)：42-44 Zhang C G.The choice of modern storage silos[J].Grain and Oil Storage Science and Technology Communication，2002(2)：42-44

[3]曾丁，黄文彬，华云龙.筒仓壁压的有限元分析[J].农业工程学报，1998，14(2)：44-48 Zeng D，Huang W B，Hua Y L.Finite element analysis of silo wall pressure[J].Transactions of the CSAE，1998，14(2)：44-48

[4]石翠霞.筒仓内小麦、玉米堆的压缩特性、仓壁压应力及储粮总重量的研究[D].南京：南京财经大学，2011 Shi C X.The study on compression characteristics of wheat piles and maize piles，the stress on the wall and the total weight of the grain storage in silos[D].Nanjing：Nanjing University of Finance and Economics，2011

[5]严晓婕.稻谷堆与籽粒的压缩特性及其在筒仓中密度与应力分布的研究[D].南京：南京财经大学，2014 Yan X J.The compression properties of paddy heap and paddy grain and study on density and stress distribution of paddy in silos[D].Nanjing：Nanjing University of Finance and Economics，2014

[6]任正晓.粮食库存检查实务[M].北京：中国商业出版社，2007：15-17 Ren Z X.Grain inventory examination practice[M].Beijing：China Commercial Publishing House，2007：15-17

[7]Mahmoud A A.Loading on shallow cylindrical flexible grain bins[J].Journal of Powder Bulk Solids Technology，1981(5)：12-19

[8]Zhang Q.Static and thermal loads in full size grain bins predicted by vectorized FEM on supercomputer[J].Transactionsof the ASAE，1989，32(2)：685-691

[9]Ruckenbrod C，Eibl J.Numerical results to discharge processes in silos[J]. Reliable flow of particulate Solids. 1993，503-516

[10]Ragneau E，Ooi J Y，Rotter J M. Finite element models for specific applications[J]. Brown C J，Nielsen J，editors. Fundamentals of theory behavior and design.1998,595-608

[11]Goodey R J，Brownb C.J，RotterJM.Predicted patterns of filling pressures in thin-walled square silos[J].Engineering Structures，2006，28：109-119

[12]Loewer J O，Ross I J，Kratzer D D，et al.and Walker，J.N.Properties of ground shelled corn as related to forces in bulk storage structures[J].Transactions of the ASAE，1977，20(1)：155-156

[13]Thompson S A，Ross I J.Compressibility and frictional coefficients of wheat[J].Transactions of ASAE，1983，26(4)：1171-1176

[14]Moya M，Aguado P J，Ayuga F.Mechanical properties of some granular agricultural materials used in silo design[J].International Agrophysics，2013，27：181-193

[15]陈德民，张元.基于压力传感器网络的粮仓储粮数量监测系统[J].微计算机信息，2009，25(13)：142-144 Chen D M，Zhang Y.The system of monitoring the number of grain storage based on the pressure sensor network[J].Microcomputer Information，2009，25(13)：142-144

[16]杨平.土力学[M].北京：机械工业出版社，2005：98-107 Yang P.Soil mechanics[M].Beijing：Machinery Industry Press，2005：98-107

[17]Rankine W J M.On the stability of loose earth.[J].Philosophical Transactions of the Royal Society Londen，1857，147：1-9

[18]Janssen H A.Versuche über getreidedruck in silozellen[J].Zeitschriff des Vereines Deutscher Ingenieure，1895，39：1045-1049.

The Model of Density and Pressure Distribution of Paddy in the Hopper-Bottom Silo

Du Xiaocui Yan Xiaojie Cheng Xuduo Gao Mengyao Feng Jiachang

(College of Food Science and Engineering;Nanjing University of Finance and Economics;Collaborative Innovation Center for Modern Grain Circulation and Safety Jiangsu Province，Nanjing 210046)

The LHT-1 rebound modulus tester was used to determine the compression density of paddy.The differential equations of density，stress and grain layer depth in hopper-bottom silo were built.Numerical method was used to obtain the relationship of density，pressure and depth and then the total weight of paddy was calculated by integration.Experimental results show that as the average vertical stress of paddy(00.495～245.892 kPa)，the compression density of Huaidao No.5 paddy increased from 582.772～696.593 kg/m3in the moisture range of 10.38%～18.30% w.b.Model calculation results showed that in a silo with a cone hopper，density of paddy in cylinder of silo increased with the paddy depth，the density of paddy in cone hopper decreased with the increase of depth.The vertical stress acting on the paddy in cylinder part of silo increased with depth of paddy，and then decreased with the increase of depth in cone hopper.The lateral stress acting on the paddy in cylinder of silo increased with depth，then increased sharply in the junction of cylinder and cone hopper，the lateral stress of paddy in the cone hopper first increased slightly，and then decreased with the increase of depth of paddy heap.

hopper-bottom silo，paddy，density，vertical stress，lateral pressure

国家自然科学基金(31371856)，公益性行业(粮食)科研专项(201313001)

杜小翠，女，1991年出生，硕士，粮食储藏工程

程绪铎，男，1957年出生，教授，粮食储藏工程

TS210.4

A

1003-0174(2017)05-0102-08