基于S变换模矩阵的电能质量暂态检测①

杨丹丹, 关维国

(辽宁工业大学 电子与信息工程学院, 锦州 121001)

基于S变换模矩阵的电能质量暂态检测①

杨丹丹, 关维国

(辽宁工业大学 电子与信息工程学院, 锦州 121001)

针对配电网暂态电能质量扰动分类方法复杂度高和扰动定位不精确的问题, 提出了一种基于S变换模矩阵与分类规则树的扰动自识别及定位方法. 该方法通过对信号进行S变换进而从变换结果中提取四个特征量判据, 然后基于分类规则树形成自识别方法; 再采用S变换模矩阵的幅值包络方法和幅值平方和均值方法, 检测扰动信号的幅度变化以及定位起止时间. 通过仿真验证该方法能够以较低的复杂度完成对扰动信号的快速、准确分类与定位.

电能质量; 暂态扰动; S变换模矩阵; 特征量; 分类与定位

1 引言

由于电力系统中投入使用大量的的非线性设备、冲击性负载等, 导致电力系统中电能质量问题以及不良影响大幅度增加, 如谐波污染、电压暂降等[1,2]. 随着对高品质生活追求的深入化, 人们开始对电能质量的优质度及供电可靠性提出了更高的要求, 因此对电能质量进行准确分类和定位分析已然成为必要.

针对暂态扰动信号的分析方法主要包括: 快速傅里叶变换[3,4], 小波变换[5,6], S变换方法[7,8]等. 快速傅里叶变换更多的应用于分析平稳信号, 对于暂态扰动信号的分析, 信号的高频和低频的特性不能同时体现, 易造成分析精度不良. 小波变换是一种可针对扰动信号的时间和频率进行局部化分析的方法, 且具有良好的正交性等优点, 但对信号的低频和高频部分分析模糊,易受噪声的干扰. 针对扰动信号分类的主要包括: 支持向量机[9]、人工神经网络[10]等, 但这些方法对扰动信号进行分类时需要较长的训练时间, 且分类步骤繁琐.S变换针对暂态电能扰动信号的分析具备良好的分析识别优势. 文献[11]和文献[12]提出采用S变换的等值线和基波曲线的方法针对扰动信号的检测及分类, 但是都存在曲线突变边沿变化不够明显的弊端, 容易导致对扰动信号不能进行准确检测和定位的后果.

本文基于S变换模矩阵的方法实现对配电网暂态电能质量的识别和定位, 首先, 对扰动信号进行S变换从而获取其四个特征量判据, 然后, 通过分类规则树原理完成对扰动信号分类的目的, 最后, 定位扰动时间和检测幅度变化. 本文提出的方法只需提取四个特征量判据, 方法简单有效, 具备良好的抗噪声能力.

2 S变换模矩阵原理

S变换是一种可逆的时频局部分析方法[13], 给定信号x(t)的一维S变换表达式为:

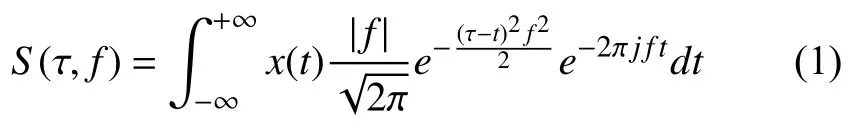
通过快速傅里叶变换可推到出信号x(t)的离散S变换, 与傅里叶反变换X(f)函数关系如下:

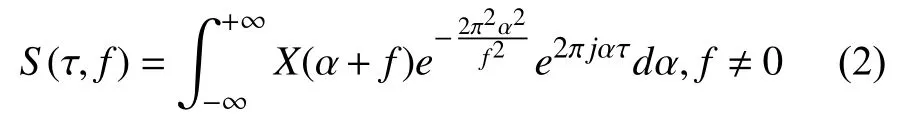
式(2)中, X(α+f)为信号x(t)频率平移α后的傅里叶反变换形式. 信号的离散S变换获取方法如下, 对于给定的电能信号x(t)进行离散采样, 得到时间序列x[kT]. 对式(2)离散化处理, 令τ=iT, f=n/NT, T是采样间隔, N是采样点数. 则一维离散S变换表示:

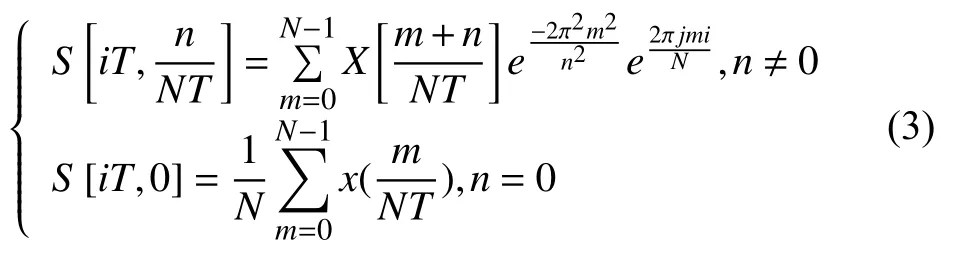
其中, i, m, n=0, 1, 2,..N-1. 对离散时间序列x[kT]进行离散S变换处理, 获得一个矩阵为S矩阵, S矩阵可表示为:

将S矩阵中的各个元素求取模值之后, 所得到的矩阵称作S模矩阵, 记为S’.

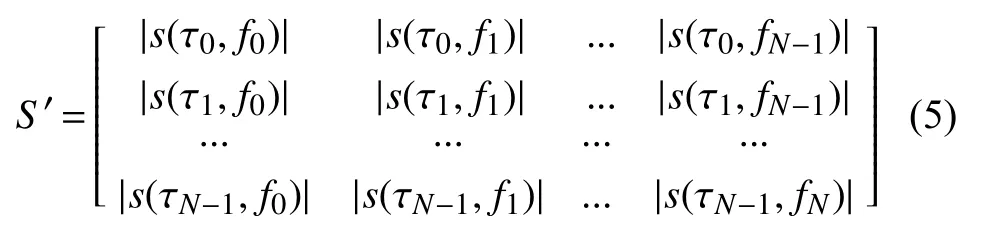
S模矩阵中, 行元素表示在某一时刻的信号幅值随频率的改变而变化; 列元素表示在某频率处的信号幅值随时间的改变而变化. 针对扰动信号的检测, STFT、小波变换因窗函数大小固定导致定位可能不精准; 以及对于发生在零点时的扰动信号定位困难等. 图1是暂升信号S模矩阵的三维立体图, S变换模矩阵突破窗函数固定不变的弊端, 同时包含扰动信号的全面信息, 不会因为在零点发生扰动而缺失信息, S模矩阵包含的丰富信息可准确检测信号突变点、幅值变化以及适合提取特征量判据.

图1 电压暂升S模矩阵三维立体图

3 暂态扰动信号的分类与定位方法

本文基于S变换模矩阵原理, 针对暂态电能质量扰动建立分类与定位的自识别方法. 首先, 根据对扰动信号的时频分析, 通过等值线所包含的数据描述扰动信号随时间变化的频率分布. 然后, 在S模矩阵中提取四个特征量, 作为分类规则树的四个判据, 并根据分类规则树方法对信号进行识别分类, 最后, 针对扰动信号时间的定位, 确定幅值平方和均值曲线上的尖峰点, 从而可确定扰动发生的起止时刻; 确定时间幅值包络的最大(小)点, 检测其幅值变化.

3.1 暂态扰动信号分类与定位原理

扰动信号在某时刻或频率处的幅值大小可通过矩阵中相应元素的值反映出来. 通过确定S矩阵中每行或列的最大模值, 建立扰动信号的频率幅值包络线或时间幅值包络. S矩阵中元素的幅值表示为:

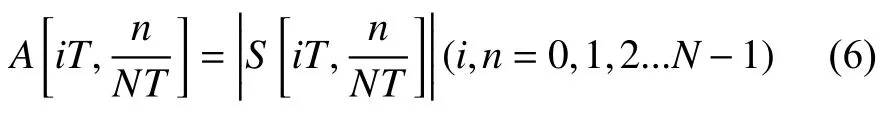
式(6)中, i, n=0, 1, 2,..N-1. 扰动信号所含的频率成分可以通过其频率幅值曲线直接反映处理; 时间幅值包络可检测幅度变化的大小.

信号发生突变可直接通过S模矩阵中相应的某一列或几列幅值平方和均值的波动进行描述.

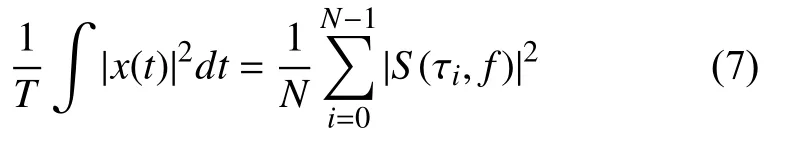
根据Parsel定理, 信号的总能量是各时刻能量总和,等式右边表示在扰动频率f时各时间点的对应的能量总和.

3.2 暂态扰动信号分类算法

S模矩阵中的元素, 包含了扰动信号其幅值或频率发生突变的状况, 故通过对S模矩阵提取信号4个特征量判据, 并结合分类规则树对多种暂态扰动分类.

1) 频率成分判据A: 根据式(8)获得扰动信号的频率幅值包络.

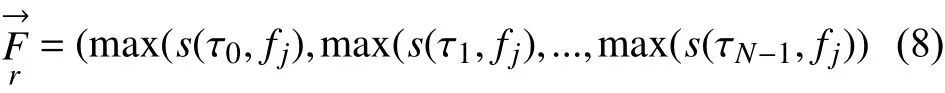
式(8)中, j=0, 1, 2,..N-1.

通过式(9)幅值包络曲线斜率的变化, 确定频率幅值包络的极大值点, 从而确定主要频率个数. 当A=2, 信号为暂态振荡; A＞2, 表示的谐波及含有谐波信号;A=1, 表示只含有基波的信号.

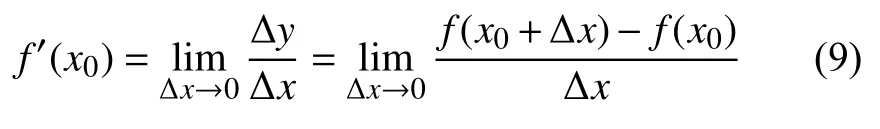
2) 扰动时间判据B: 扰动信号的时间定位数, 根据式(10)建立扰动信号的时间幅值平方和均值曲线, 同理确定扰动尖峰点数. B=0, 谐波信号; B=1, 信号为暂态脉冲; B=2, 为暂升或暂降等信号.

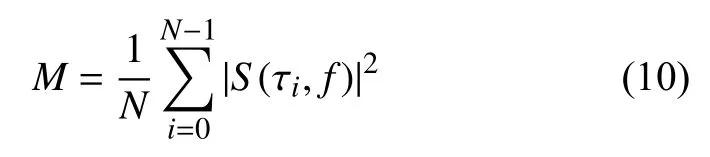
3) 幅值升降判据C: 时间幅值包络曲线的变化; 在S模矩阵中逐列求最大模值, 确定S变换幅值包络向量,标记求“修正一阶中心距[14]”, 通过一阶距的正负, 反映信号的隆起和凹陷, 即C＞0, 扰动信号为暂升或包含谐波, 反之, 扰动信号为暂降或包含谐波.

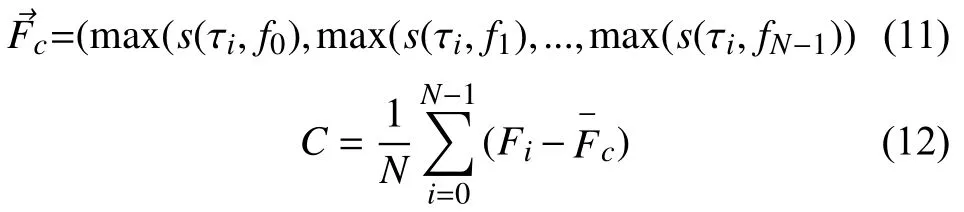
式(11)中, i=0, 1, 2,..N-1, 式(12)中的长度是N,表示信号的时间幅值包络向量的平均值,该信号长度为N且不含扰动成分.

4) 电压跌落判据D: 根据式(13)计算幅值下降程度.其中: D为电压下降度, A是时间幅值包络数据构成的矩阵, j是矩阵A中最小值对应的点, i是在最小值点处前后各取的点数.

此处i取10. 当10%≤D≤90%时, 扰动信号为暂降; 当90%≤D≤100%时, 扰动信号为中断.

针对常见的几种配电网暂态电能质量扰动信号,根据以上提取的四种特征量判据可对扰动信号进行分类, 分类步骤如图2所示.

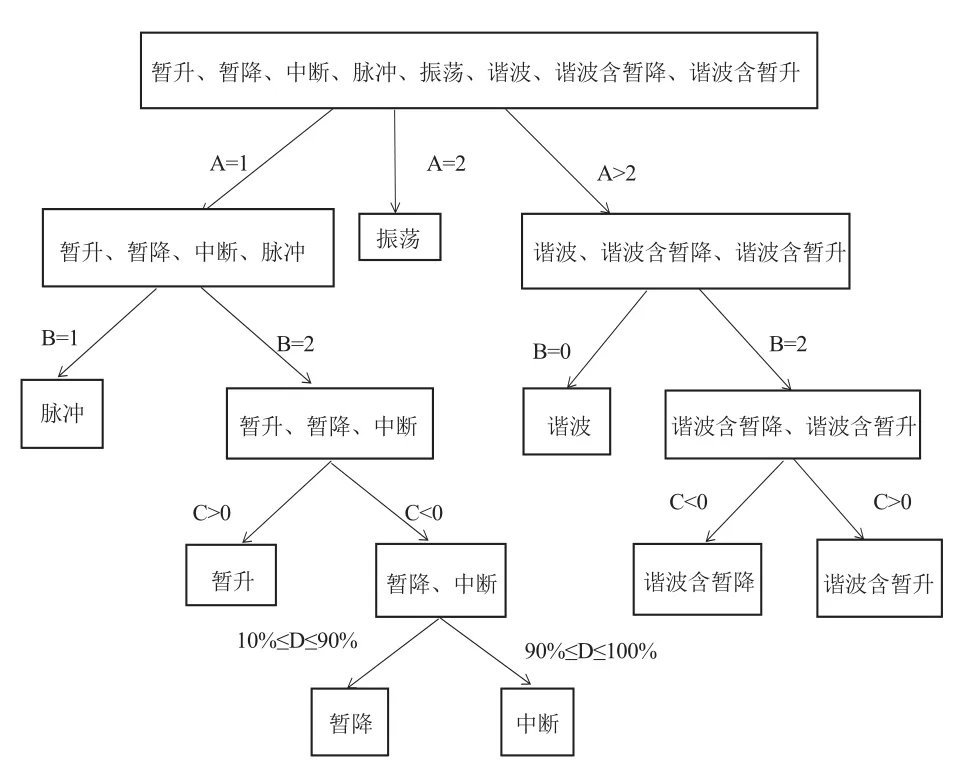
图2 扰动分类规则树

3.3 暂态扰动信号的定位分析

信号发生突变可直接通过S模矩阵中相应时间点或频率处的幅值变化显示出来, 故针对扰动信号起止时刻的定位, 可通过式(13)确定时间幅值均方和曲线的峰值点实现.

针对配电网中暂态扰动信号的幅度检测, 研究类型包括电压暂降、暂升和中断. 本文针对暂降和中断信号的幅度变化检测可根据式(13)计算. 针对电压暂升扰动的幅度变化检测可根据式(14)计算.

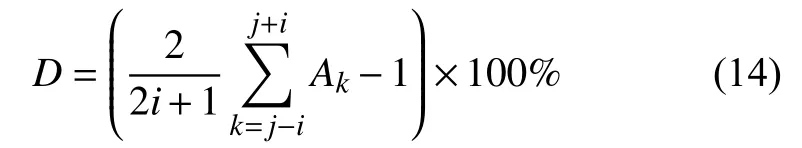
式(14)中, D为幅值上升度, 首先确定扰动信号的幅值包络曲线上最大值对应点j, i表示在最大值点前后各取的点数, 此处i取10, 暂升扰动幅度范围为10%≤D≤80%.

4 S变换的暂态扰动信号仿真验证

通过软件对配电网中常见的暂态扰动信号进行仿真, 波形如图3～图6所示. 各图中子图(b)是信号的等值线, 通过等值线图反映了扰动信号的时频分布状况. 子图(c)为扰动信号的频率幅值包络, 通过曲线峰值反映其含有的频率成分, 图3(c)和图6(c)中, 频率幅值包络均在工频处出现尖峰, 表示信号只含基波成分; 图4(c)中,信号分别在50 Hz, 150 Hz, 250 Hz处出现尖峰, 表示信号含有基波频率, 三次谐波和五次谐波成分; 图5(c)中分别在50 Hz和900 Hz处出现尖峰, 表示信号除基波成分外还包含高频成分, 通过仿真表明检测到的频率成分与实际情况一致. 子图d是时间幅值平方和均值曲线,在图3～图6中均出现两个明显的峰值点, 这两点分别对应扰动信号发生突变的起止时刻. 子图e是扰动信号的时间幅值包络曲线, 通过图3、图4、图6的时间幅值包络实现对扰动信号幅度变化的检测, 其检测值与设定值相差无几.

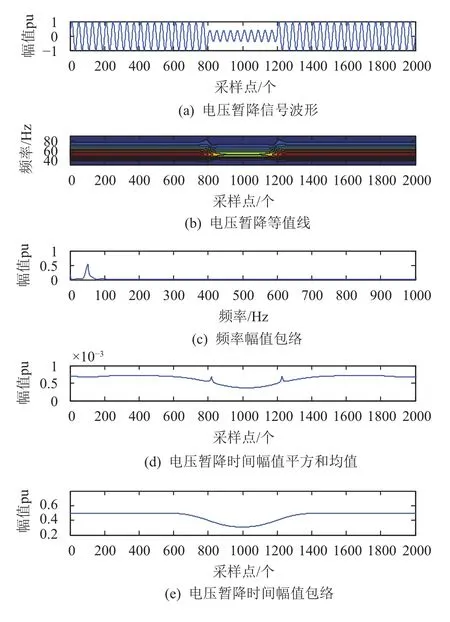
图3 电压暂降

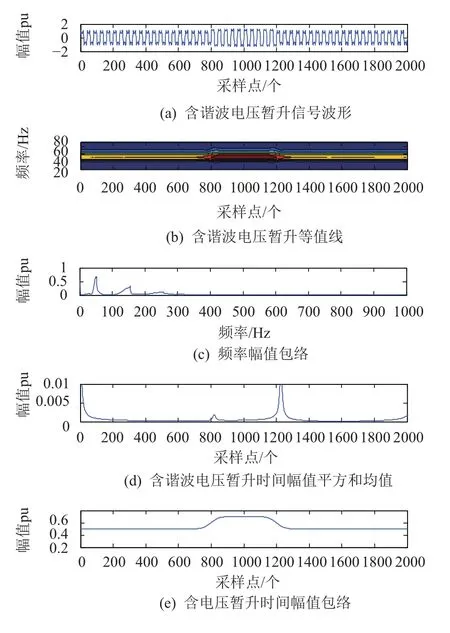
图4 暂升含谐波

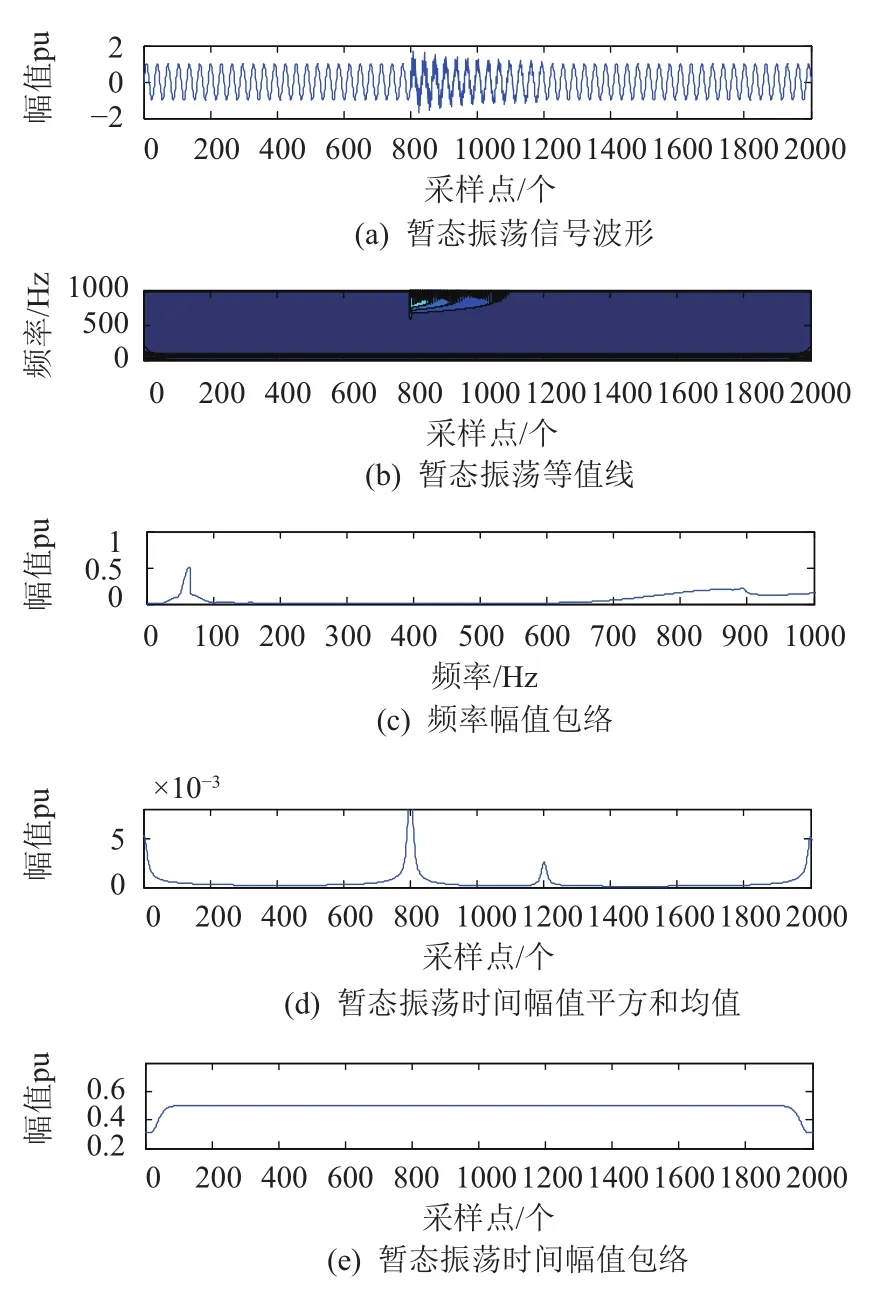
图5 暂态振荡

图6 电压中断

4.1 扰动信号的分类仿真分析

按照图2的扰动类型随机产生200个测试样本, 在信噪比为20 dB、30 dB的噪声环境下进行仿真, 并同SVM分类结果对比, 其测试结果如表1所示.

通过表1测试表明, 在不同噪声程度的环境中, 本文提出的方法均达到良好的分类效果. 在含有较大噪声的情况下, 分类准确率仍可保证在95%以上, 可见此分类方法具有较高的准确性.

4.2 扰动信号的定位仿真分析

根据S变换模矩阵对扰动信号的定位方法, 表2列出针对四种扰动信号的定位结果, 包括扰动信号的起止时刻、幅度变化以及相对误差. 由表2可见, 对于配电网电能质量信号的检测结果, 扰动持续时间的准确度控制在1%内, 幅度变化的误差均在2%内, 检测值与实际值相差甚小, 验证了该方法具有检测精度高的优点.

5 结论

本文针对配电网暂态扰动信号的分析提出了一种基于S变换模矩阵与分类规则树相结合的方法, 该方法提取的特征量判据少, 快速准确的实现对扰动信号的分类, 并且有良好的抗噪优势. 该方法通过信号的幅值平方和均值和幅值包络, 准确对信号定位以及幅度变化的检测. 仿真验证此方法可快速、准确的对扰动信号进行识别和定位. 本文提出的基于S变换模矩阵的分类与定位方法可实现对配电网中电压暂升、中断等扰动信号的参数确定, 检测精度高, 满足实际工程需求.

表1 扰动分类测试结果

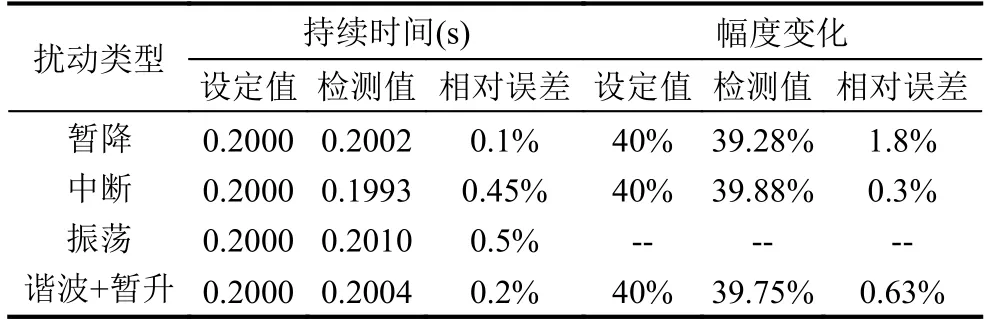
表2 扰动信号检测结果

1林琳, 伊德富. 电力系统电能质量问题探析. 机电信息, 2012,(21): 25, 27.

2杨璐. 电能质量及检测方法研究. 通信电源技术, 2015, 32(6):28–30, 32.

3徐永海, 赵燕. 基于短时傅里叶变换的电能质量扰动识别与采用奇异值分解的扰动时间定位. 电网技术, 2011, 35(8):174–180.

4张斌, 孙静. 基于Mallat算法和快速傅里叶变换的电能质量分析方法. 电网技术, 2007, 31(19): 35–40.

5潘从茂, 李凤婷. 基于小波变换的暂态电能质量的检测与识别. 电测与仪表, 2013, 50(11): 69–72. [doi: 10.3969/j.issn.1001-1390.2013.11.016]

6魏荣进, 江亚群, 黄纯, 等. 基于小波变换的电压暂降实时检测方法. 计算机工程与应用, 2013, 49(11): 252–256. [doi:10.3778/j.issn.1002-8331.1110-0330]

7Reddy MJB, Raghupathy RK, Venkatesh KP, et al. Power quality analysis using discrete orthogonal S-transform(DOST). Digital Signal Processing, 2013, 23(2): 616–626.[doi: 10.1016/j.dsp.2012.09.013]

8刘奇, 周雒维, 卢伟国. 基于广义S变换的暂态电能质量扰动定位与识别. 电力系统保护与控制, 2012, 40(7): 60–65.[doi: 10.7667/j.issn.1674-3415.2012.07.011]

9杜林, 李欣, 司马文霞, 等. S变换模矩阵和最小二乘SVM在雷电及操作过电压识别中的应用 .电力自动化设备 ,2012,32(8): 35–40.

10尹柏强, 何怡刚, 朱彦卿. 一种广义S变换及模糊SOM网络的电能质量多扰动检测和识别方法. 中国电机工程学报,2015, 35(4): 866–872.

11谷金宏, 刘琪, 程超会. 电能质量的S变换仿真. 电测与仪表, 2009, 46(6): 51–55, 62.

12吕干云, 程浩忠, 郑金菊, 等. 基于S变换和多级SVM的电能质量扰动检测识别. 电工技术学报, 2006, 21(1): 121–126.

13Kazemi K, Amirian M, Dehghani MJ. The S-transform using a new window to improve frequency and time resolutions.Signal, Image and Video Processing, 2014, 8(3): 533–541.[doi: 10.1007/s11760-013-0551-1]

14杨洪耕, 刘守亮, 肖先勇. 利用S变换时频等值线图与幅值包络向量实现电压凹陷的分类. 电工技术学报, 2006, 21(8):75–79, 126.

Detection of Transient Power Quality Disturbances Based on S-Transform Module Matrixes

YANG Dan-Dan, GUAN Wei-Guo
(College of Electronic and Information Engineering, Liaoning University of Technology, Jinzhou 121001, China)

In view of the complex identification and inaccurate disturbance location of distribution network transient power quality, a disturbance self recognition and localization method based on S-transform matrixes and classification rule tree is proposed. The method analyzes signals by the S-transform and extracted four characteristic quantities from them, then the classification of disturbance signals is performed by use of a rule-based decision tree; and then the disturbances’ amplitude change and start-stop time are detected using the amplitude envelope algorithm and amplitude square sum algorithm of S-transform matrixes. The simulation results show that the method is fast and accurate to identify and locate the disturbance signal with low complexity.

power quality; transient disturbance; S-transform module matrixes; characteristic quantity; identification and localization

杨丹丹,关维国.基于S变换模矩阵的电能质量暂态检测.计算机系统应用,2017,26(7):183–188. http://www.c-s-a.org.cn/1003-3254/5844.html

辽宁省自然科学基金计划面上项目(201700531)

2016-10-18; 收到修改稿时间: 2016-11-28