面向人脸识别的判别低秩字典学习算法①

利润霖

(中国石油大学(华东) 计算机与通信工程学院, 青岛 266580)

面向人脸识别的判别低秩字典学习算法①

利润霖

(中国石油大学(华东) 计算机与通信工程学院, 青岛 266580)

人脸识别是计算机视觉和模式识别领域的一个研究热点, 有着十分广泛的应用前景. 人脸识别任务在训练样本和测试样本同时包含噪声的情况下存在识别精度不高的问题, 为此本文提出一个新的判别低秩字典学习和低秩稀疏表示算法(Discriminative Low-Rank Dictionary Learning for Low-Rank Sparse Representation, DLRD_LRSR).本文方法在模型中约束每个子字典和稀疏表示低秩避免噪声干扰, 并引入了判别重构误差项增强系数的判别性. 为验证算法的有效性, 本文在3个公开人脸数据集上进行了实验评估, 结果表明与现有字典学习算法相比, 本文算法能够更好的解决训练样本和测试样本同时存在噪声的人脸识别问题.

字典学习; 低秩矩阵恢复; 人脸识别; 增广拉格朗日乘子算法

经过几十年的发展, 稀疏编码已经变成一项热门课题, 被神经系统学科、信息理论、信号处理等相关领域的专家所研究[1-5]. 字典学习通常用于对信号进行稀疏编码, 通过一个完备字典中的少部分元素线性组合实现对样本的重构. 在计算机视觉领域中, Olshausen和Field[1]于1996年提出了一个关于对人类视觉系统细胞感受野建模的方法, 首次提出稀疏和过完备图像表示的概念. 在此基础上研究者提出许多字典学习算法并成功地应用于人脸识别[4,6], 图像分类[7,8], 子空间聚类[9], 图像恢复[10], 运动分割[11]等领域.

Wright et al.[4]提出了一种基于稀疏编码的分类算法(SRC), 该算法将训练样本组成的矩阵作为字典, 通过优化重构误差求取样本的稀疏表示并用于分类. 为了提高SRC算法的性能, 许多研究者对其做出了改进[12-14],虽然这些算法都具备了很强的鲁棒性, 但是在训练样本过多的情况下会得到维数过高的字典, 从而导致空间和时间代价的增加. 为了避免字典维数过大的问题,一些低维字典学习的方法先后被提出. KSVD[15]在字典学习过程中依据误差最小原则, 对误差项进行SVD分解, 选择使误差最小的分解项作为更新的字典原子和对应的原子系数. 利用KSVD算法得到的字典对样本重构可以得到理想的效果, 但是该方法只关注于稀疏表示和字典原子对原始样本线性重构的误差大小, 并没有将字典的判别性考虑在内. 在KSVD的基础上, Mairal et al.[8]通过在目标函数中加入判别重构约束增加稀疏表示的判别力. Zhang和Li et al.[16]提出了用于人脸识别的判别KSVD算法(D-KSVD), 该方法将线性分类器融入了目标函数, 最终的目标函数可通过KSVD的求解方法对字典和分类器进行共同学习. 在此基础上, Jiang et al.[17]提出LC-KSVD算法, 通过在目标函数中加入标签一致约束项, 增强字典的判别性. Lee et al.[18]和Wang et al.[19]提出了一种特殊的判别准则去学习过完备的字典,有效地降低了计算的复杂度. Yang et al.[20]根据费舍尔准则构建了一种判别重构误差约束, 并将字典定义为多个子字典的组合, 在迭代更新过程中减少类内的重构误差和类间重构增强字典判别力. 上述算法可以学习得到具有判别力的字典, 但是这些方法适用前提是图像不存在噪声(如KSVD、LC-KSVD)或者是图像训练图像不存在噪声(如SRC), 在训练样本和测试样本同时存在噪声的情况下, 训练数据存在噪声使得字典训练难度的增加, 极大影响分类的结果, 本文对比实验中也证实了这一点, 针对这一问题, 研究者提出了基于低秩表示的字典学习方法.

低秩矩阵恢复的方法在这几年里得到了迅速的发展[21-23], Wright et al.[24]提出的RPCA算法通过低秩矩阵恢复和填充算法框架寻找数据潜在的低秩结构, 得到强鲁棒性的低维表示. 由于其鲁棒特性, RPCA成功地被运用于背景去除[25], 目标检测[26], 目标跟踪[27]等领域. 在图像分类中, Chen et al.[28]利用低秩矩阵恢复去除训练样本中的噪声, 在人脸识别任务中获得了强鲁棒性的结果. Liu et al.[29]提出了低秩表示算法(LRR),LRR算法通过优化得到能够与字典对样本进行重构的低秩矩阵. 利用低秩矩阵LRR在子空间分割中有着非常理想的性能. 基于LRR算法, 一系列面向图像分类的字典学习方法先后被提出. Ma et al.[30]提出了判别低秩字典学习算法(DLRD_SR), 通过在目标函数中加入对子字典的低秩约束, 有效抑制了训练样本存在噪声的干扰, 学习得到干净的低秩字典, 并在训练样本与测试样本同时存在噪声的人脸识别实验中得到了显著的效果. 为了增强DLRD_SR算法的字典判别性, Li et al.[31]将费舍尔判别准则融入目标函数, 提出了面向图像识别的判别低秩字典学习算法(D2L2R2). Zhang et al.[32]提出结构化低秩表示算法, 通过在LRR的目标函数中加入稀疏表示的结构化正则项得到具有判别力的低秩表示, 该方法并没有在字典更新阶段加入有效约束, 针对这个缺陷, DLR_DL算法[33]在字典更新阶段加入低秩约束, 增强了字典对样本的表达能力. 然而文献[32,33]在稀疏编码过程中忽视了类内聚合以及类间区分能力.

现有的基于低秩表示的方法虽然能够有效处理训练样本和测试样本同时存在噪声的问题, 但是忽略了稀疏编码和字典更新过程中判别性约束的统一性,DLRD_SR和DLR_DL在稀疏编码过程中都没有采取有效措施深入挖掘样本类内聚合以及类间区分能力, 而LSLRR是在字典更新过程中忽视了字典的判别性约束. 对此, 本文提出一个新的判别低秩字典学习方法,在编码阶段约束稀疏表示低秩并加入新的判别约束确保稀疏表示更具判别力; 在字典更新阶段, 通过约束子字典低秩让学习到的字典更加干净和紧致; 本文算法通过逐类更新子字典和以及低秩稀疏表示的方式, 有效提高了训练类内的聚合力以及类间的区别力. 不同于DLRD_SR算法, 本文算法编码过程中加入判别约束并约束稀疏表示低秩, 从而让学习到的低秩稀疏表示具有更高的判别力. 与DLR_DL相比, 本文方法在编码和字典更新过程中使用了统一判别重构误差约束, 能够更好的保留原始数据中结构信息. 实验结果证明, 与现有字典学习算法相比, 本文提出的DLRD_LRSR算法在存在噪声的人脸识别任务中具有更好的性能表现.

1 相关工作

1.1 低秩矩阵恢复

假设矩阵X可以被分解为两个矩阵, i.e., X=A+E,A为低秩矩阵, E为稀疏噪声矩阵. 低秩矩阵恢复旨在找到一个低秩的A近似表示X. 低秩矩阵恢复可以视为以下优化问题:

λ为噪声矩阵E权重参数. 因为求解(1)是一个NP-hard的问题. 为了能够求解问题(1), 文献[24]证明了在矩阵A为低秩且E为稀疏矩阵情况下, 问题(1)可以等价于:

1.2 低秩表示

在图像分类问题中, 可以认为相同类别的样本特征来自同一子空间, 而不同类别的样本特征分别来自不同子空间. 文献[29]证实了存在一个低秩的矩阵可以揭示样本之间的成员关系, 并提出了低秩表示算法(LRR),可以公式化为:

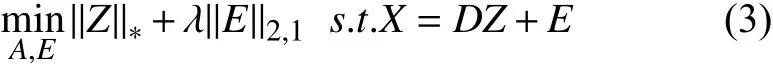
1.3 低秩字典学习

文献[30]提出了低秩字典的算法(DLRD_SR),DLRD_SR通过约束子字典低秩, 在训练字典的过程中减少训练样本存在噪声的影响进而学习到干净的低秩字典. 给出一组数据, Xi为i类的样本, c为样本类别的数量, d为特征的维数, N为训练样本的总数. X中可能会包含噪声, 如遮挡, 像素缺失以及光照阴影等. 低秩矩阵恢复可以将受噪声干扰的矩阵X分解为一个低秩组合矩阵DZ和一个稀疏的噪声矩阵E, i.e., X=DZ+E. 假设字典包含c个子字典, 其中K为字典的维数大小, Di为类i子字典.为低秩稀疏表示, Z可以表示为DLRD_SR算法模型可以公式化为:

Zi为Xi相对于字典D的稀疏表示, Zi,j为Xi相对于字典Dj的稀疏表示,. 文献中实验结果证明DLRD_SR能够很好处理人脸识别任务中存在噪声的问题.

受到相关工作启发, 本文提出一种新的用于人脸识别的低秩字典学习算法, 减少存在训练样本中的噪声干扰, 学习干净字典以及具有判别力的低秩稀疏表示. 通过约束每个子字典和稀疏表示低秩, 有效减少噪声干扰, 并在编码过程中加入新的判别重构误差项, 增强低秩稀疏表示的判别力. 实验表明本文算法有以下优点:

1)本文方法通过约束每个子字典低秩, 有效减少噪声的干扰, 获得干净紧致的低秩字典. 低秩字典能够有效提高稀疏表示的判别力.

2)引入判别重构误差项, 逐类更新子字典和以及低秩稀疏表示, 增强了字典和低秩稀疏表示的判别力,提高了分类精度.

2 DLRD_LRSR模型

为了解决人脸识别任务中存在噪声的问题, 本文提出一个新的判别低秩字典学习算法. 本文的模型可以表示为:

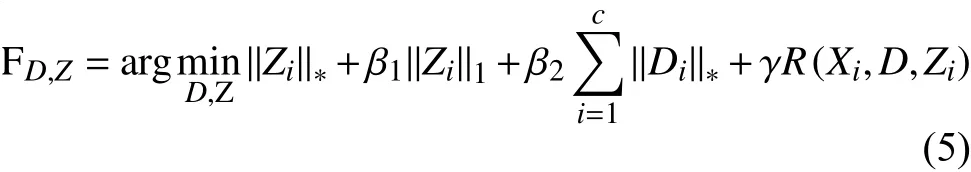
Zi可以进一步表示为, 其中Zji为子字典Dj相对于Xi的低秩稀疏表示. 假设Xi为未受噪声干扰的样本, 则样本能够被字典和稀疏表示重构,所以有, 因此我们约束和最小化(为Frobenius范数), 而矩阵的元素值也应接近于零, 从而使的值最小化. 由此, 定义判别重构误差项为:

加入重构误差项, 本文的模型可以表示为:

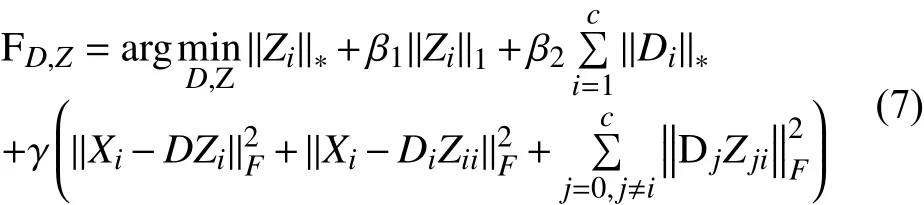
本文的模型可以通过迭代优化字典D和低秩稀疏表示Z求解, 具体步骤在第3节中提出.

3 优化

为了求解公式(7)的优化问题, 可以将模型优化分解为两个子问题: 首先, 固定字典D以及对逐个进行更新, 合并所有Zi可以获得低秩稀疏表示矩阵Z; 然后固定逐个更新子字典Di. 通过迭代这两步最终可以得到最优化的低秩字典D.

3.1 更新X

假设字典D固定, 原始的目标函数(7)可以视为稀疏编码问题, 固定逐个进行更新, 可以通过求解以下问题来实现:

为在不受噪声的影响的情况下得到低秩稀疏表示.本文在判别重构误差项中加入噪声项Ei.为了求解公式(10)引入两个辅助变量H和W, 可以化为以下等价形式:

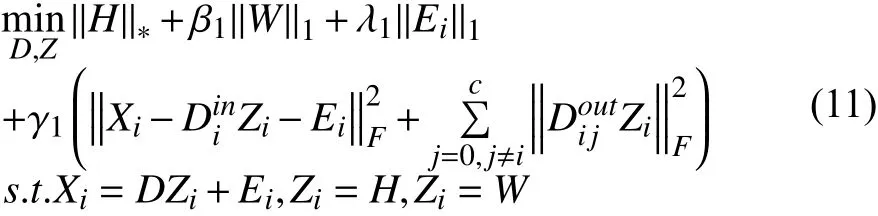
这个优化问题可以通过增广拉格朗日乘子方法[38]求解, 将公式(11)转化为以下增广拉格朗日函数:

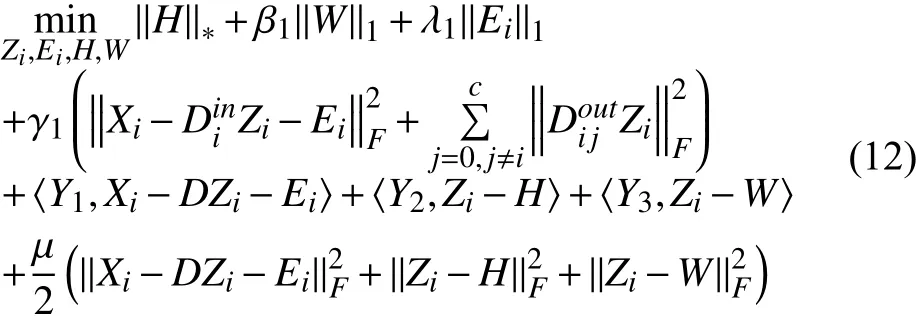
式中, 〈A,B〉=trace (ATB); Y1、Y2、Y3为拉格朗日乘子; μ为正数惩罚因子. 通过逐个更新H, Zi, W, Ei来求解问题(11), 算法1归纳了求解的过程.

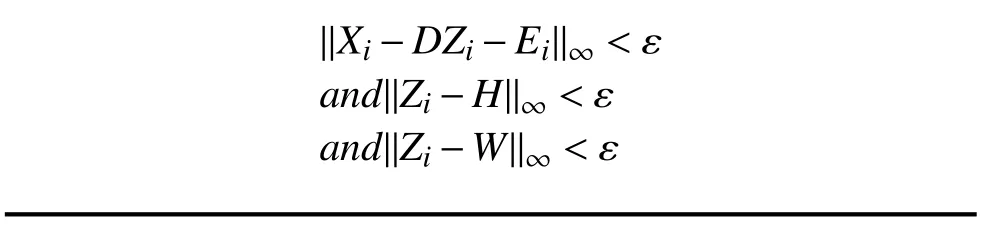
3.2 更新D

得到优化系数Z后, 固定然后对Di逐个进行更新. 当Di更新后, Xi相对于Di的稀疏表示Zii也应得到更新. 可以得到以下目标函数:

公式(20)可以通过依次更新L, Zii, J, Di, Ei来求解,算法2归纳了求解问题(19)的过程. 由于在更新字典时需要对字典的列向量单位化, 不能保证算法2能够收敛,因此需要设置最大迭代次数, 但是在实验中, 算法2总能在到达最大迭代次数之前就能得到收敛的结果. 在实验中, 我们使用KSVD对训练样本进行训练, 得到的字典作为本文算法的初始字典. DLRD_LRSR算法的整体流程在总结在算法3中.

3.3 分类器

通过算法3, 我们可以得到优化的判别低秩字典和训练数据X对应的低秩稀疏表示Z. 测试数据Xtest对应的表示Ztest可以通过求解以下优化问题得到:

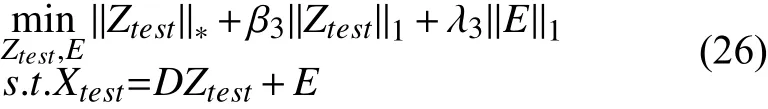
我们可以通过设置公式(11)中的参数γ1为零使用算法1求解公式(26)得到测试样本的低秩稀疏表示.

本文使用多元线性岭回归模型[27]训练分类器:

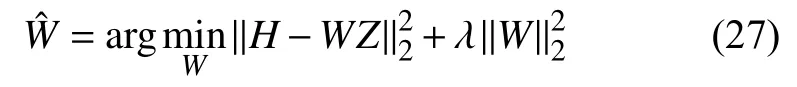
4 实验

本文在Extended Yale B[39], UMIST[40], AR[41]三个人脸数据集上对DLRD_LRSR进行了评估. 为了测试算法的性能, 本文方法与当前流行的字典学习算法进行比较, 并分别在光照变化、像素缺失、均匀分布噪声、和块遮挡的情况下测试算法的鲁棒性.

在实验中我们发现参数γ1, γ2, β1, β2, β3取值的大小对结果影响很小, 因此将它们的值都设置为1. 其他参数分别通过5-fold交叉验证得到: 对于Extended Yale B数据集λ1=5, λ2=0.09, λ3=2; 对于AR数据集 λ1=10,λ2=0.2, λ3=5; 对于UMIST数据集 λ1=10, λ2=0.2, λ3=4.

4.1 Extended Yale B数据集

Extended Yale B数据集包含38人的共2414张正脸图像, 分别在不同光照条件下拍摄, 每张图像分辨率为192×168像素, 每个人分别有59-64张图像. 本文首先将原始图像按照1/8的比例下采样得到504维的特征向量,为了测试算法在像素缺失情况下的鲁棒性, 从每张图像(包括训练和测试样本)随机选取一定比例的像素点并用255取代其像素值, 图1展示了处理后的图像样本示例. 每次实验随机从每个人的脸部图像中随机挑选32个样本作为训练集, 剩下的部分作为测试集. 本文方法分别与SRC[4]、KSVD[15]、LC-KSVD[17]、DLRD_SR[30]和LSLRR[32]算法进行对比. DLRD_LRSR和对比方法中的KSVD、LC-KSVD、DLRD_SR学习得到的字典每类包含20个原子, 共760个原子. SRC选取所有的训练样本作为字典, 包含1216个原子. 分别重复实验10次取平均值作为实验结果.

图1 Extended Yale B数据集5%像素缺失示例

表1对不同算法识别结果进行了比较, 可以看到SRC、KSVD和LC-KSVD的准确率随着噪声比例的增加而急剧下降, 而SRC得到比KSVD、LC-KSVD更高的识别结果. 证实了它们都不能很好处理噪声问题, 而SRC因为可适用于测试图片存在噪声的场景, 因此得到更高的识别结果. 而本文算法DLRD_LRSR与LSLRR、DLRD_SR在噪声存在的情况下拥有比其他方法更好的鲁棒性, 这说明了低秩约束拥有良好的抑制噪声影响的能力. 本文算法在不同比例的像素缺失实验中的准确率均大于DLRD_SR和LSLRR的识别结果, 0%～20%之间, 缺失率越高, 差距越明显, 甚至在20%像素缺失的情况下的识别结果高于LSLRR 9.46个百分点, 展示了DLRD_LRSR处理训练样本存在噪声问题的显著性能, 说明了DLRD_LRSR约束子字典和稀疏系数低秩有效降低了噪声干扰, 重构误差项能够保留噪声样本之间的判别性, 显著提高存在噪声情况下的识别精度.

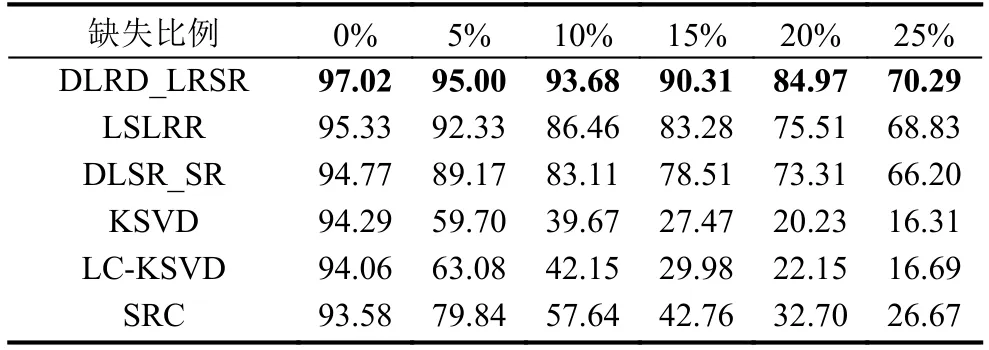
表1 Extended Yale B数据集像素缺失实验识别率(%)

4.2 UMIST人脸数据集

UMIST人脸数据集包含26人共564张人脸图像. 数据集中所有图像分辨率为112×192像素. 在本次实验中,测试本文算法在随机噪声以及块遮挡情况下的鲁棒性.选择每个人的前20张图片用于实验, 并从中随机挑选一半图像作为训练集, 剩下则作为测试集. 每张图像下采样为24×21像素. 随机噪声实验中, 图像被添加10%～50%的均匀噪声. 遮挡实验中, 用10%～50%的随机图像块遮挡图像的随机位置. 图2展示了两种噪声的示例. 本文算法分别与SRC、KSVD、LC-KSVD、DLRD_SR、LSLRR进行对比, 所有算法训练得到的字典维度大小均为训练样本个数.

图2 UMIST数据集图像示例: 第一行为添加随机噪声的图像, 第二行为添加块遮挡的图像

表2列出了不同比例块遮挡下的识别率, 表3则为不同比例均匀噪声下的识别率. 可以发现在表2和表3中SRC、KSVD和LC-KSVD的准确率随着噪声比例的增加而急剧下降, 而SRC得到比KSVD、LC-KSVD更高的识别结果, 表现出了与实验一相同的性质. 在多数情况下, DLRD_LRSR拥有比其他方法更高的准确率,特别在50%均匀噪声和50%块状遮挡比例下, 本文算法分别比LSLRR提高了1.11和0.78个百分点, 充分说明了通过约束子字典和稀疏表示低秩, DLRD_LRSR在训练过程中能够有效降低了噪声干扰, 因此在存在高遮挡和高随机噪声的场景下拥有比其他算法更高的性能.实验结果证明了本文算法中的低秩稀疏表示在存在随机噪声和块遮挡的人脸识别任务中具有显著的效果.

表2 UMIST数据集块遮挡实验识别率(%)

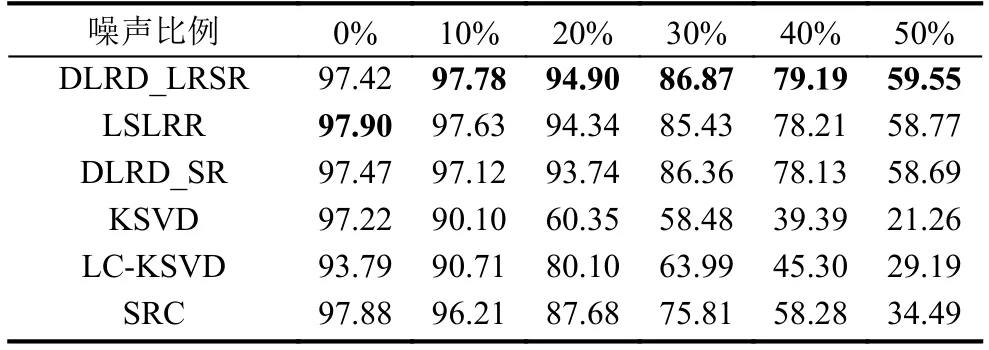
表3 UMIST数据集均匀噪声实验识别率(%)

4.3 AR数据集

AR数据集包含126人超过4000张的正脸图像. 每个人26幅图像, 分为2组, 每组每人13张, 其中未受遮挡的图像7张, 受太阳眼镜和围巾遮挡的图像各有3张, 这些图像的拍摄时间间隔为2周. 每组图像分别反映了人脸的表情、光照以及遮挡(墨镜或围巾)的变化. 在实验中, 选用了包含50个男性目标和50个女性目标的子集,并将原始图像下采样到25×20像素, 图3展示了AR图像示例, 本文算法在Sunglasses、Scarf以及Mixed三个实验中与其他方法进行比较, 三个实验设置与文献[33]一致. 本文算法分别与SRC、KSVD、LC-KSVD、DLRD_SR、LSLRR和DLR_DL[33]进行对比, 所有算法训练得到的字典维度大小均为训练样本个数. 每个实验分别重复实验10次最后求平均值作为本文方法的最后结果.

图3 AR数据集图像示例

表4列出了DLRD_LRSR与其他方法在AR数据集上的实验结果. 可以看出, SRC、KSVD和LC-KSVD算法并不能很好地解决遮挡问题, 而SRC仍比KSVD和LC-KSVD有着更高的识别结果. 与DLRD_SR、LSLRR和DLR_DL算法相比, 本文算法有了很明显的提升, 在Sunglass、Scarf和Mixed场景中分别比DLR_DL提高了3.72、4.76和5.92个百分点, 证明了本文算法能够有效的处理AR数据集中存在的光照、表情以及遮挡的问题, 并且在越复杂的场景(太阳镜遮挡比例大约20%,围巾遮挡比例大约40%, Mixed两者皆有)下DLRD_LRSR越能有显著的表现.

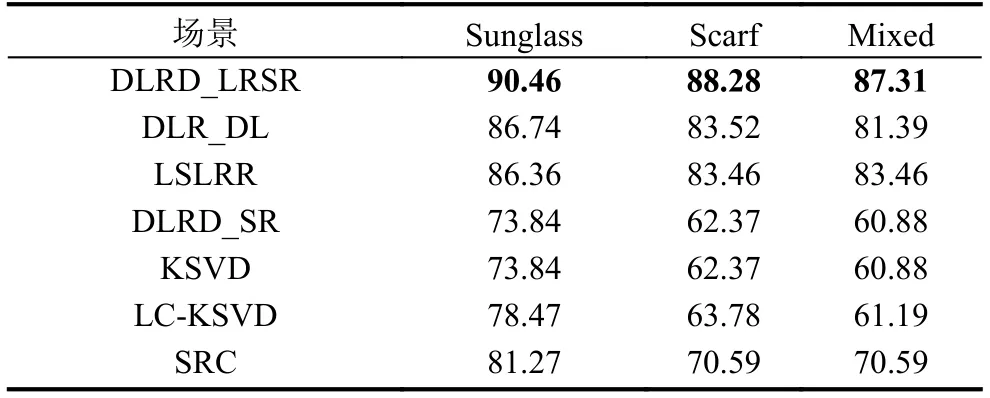
表4 AR数据集实验识别率(%)

4 结语

本文提出了一种用于人脸识别的新的判别低秩字典学习和低秩稀疏表示算法. 首先, 为了增强字典的判别力, 本文引入了判别重构误差项, 通过最小化类内重构误差以及类间重构生成低秩稀疏表示; 其次, 分别约束每个子字典和稀疏表示低秩减少了训练样本中存在噪声的干扰, 最终得到干净的字典. 本文在3个公开人脸数据集上的实验证明了本文提出的DLRD_LRSR算法在光照变化、随机噪声、像素缺失以及遮挡的情况下具有较强的鲁棒性. 由于在求解的时候采用了增广拉格朗日算法, 本文算法和大多数低秩方法一样, 存在计算效率不高的限制, 因此效率更高的低秩矩阵恢复的求解方法是我们未来要开展的工作.

1Olshausen BA, Field DJ. Emergence of simple-cell receptive field properties by learning a sparse code for natural images.Nature, 1996, 381(6583): 607–609. [doi: 10.1038/381607a0]

2Candes EJ, Romberg J, Tao T. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Information Theory,2006, 52(2): 489–509. [doi: 10.1109/TIT.2005.862083]

3Donoho DL. Compressed sensing. IEEE Trans. Information Theory, 2006, 52(4): 1289–1306. [doi: 10.1109/TIT.2006.871582]

4Wright J, Yang AY, Ganesh A, et al. Robust face recognition via sparse representation. IEEE Trans. Pattern Analysis and Machine Intelligence, 2009, 31(2): 210–227. [doi: 10.1109/TPAMI.2008.79]

5Elad M. Sparse and Redundant Representations: From Theory to Applications in Signal and Image Processing. New York: Springer, 2010.

6Wright J, Ma Y, Mairal J, et al. Sparse representation for computer vision and pattern recognition. Proc. IEEE, 2010,98(6): 1031–1044. [doi: 10.1109/JPROC.2010.2044470]

7Yang JC, Yu K, Gong YH, et al. Linear spatial pyramid matching using sparse coding for image classification. Proc.IEEE Conference on Computer Vision and Pattern Recognition, 2009. Miami, FL, USA. 2009. 1794–1801.

8Mairal J, Bach F, Ponce J, et al. Discriminative learned dictionaries for local image analysis. Proc. IEEE Conference on Computer Vision and Pattern Recognition, 2008.Anchorage, AK, USA. 2008. 1–8.

9Elhamifar E, Vidal R. Sparse subspace clustering: Algorithm,theory, and applications. IEEE Trans. Pattern Analysis and Machine Intelligence, 2013, 35(11): 2765–2781. [doi:10.1109/TPAMI.2013.57]

10Mairal J, Elad M, Sapiro G. Sparse representation for color image restoration. IEEE Trans. Image Processing, 2008,17(1): 53–69. [doi: 10.1109/TIP.2007.911828]

11Rao SR, Tron R, Vidal R, et al. Motion segmentation via robust subspace separation in the presence of outlying,incomplete, or corrupted trajectories. Proc. IEEE Conference on Computer Vision and Pattern Recognition, 2008.Anchorage, AK, USA. 2008. 1–8.

12Yang M, Zhang L, Yang J, et al. Robust sparse coding for face recognition. Proc. 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Providence, RI,USA. 2011. 625–632.

13Huang JZ, Huang XL, Metaxas D. Learning with dynamic group sparsity. Proc. 12th International Conference on Computer Vision. Kyoto, Japan. 2009. 64–71.

14Yuan XT, Liu XB, Yan SC. Visual classification with multitask joint sparse representation. IEEE Trans. Image Processing, 2012, 21(10): 4349–4360. [doi: 10.1109/TIP.2012.2205006]

15Aharon M, Elad M, Bruckstein A. rmK-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Processing, 2006, 54(11):4311–4322. [doi: 10.1109/TSP.2006.881199]

16Zhang Q, Li BX. Discriminative K-SVD for dictionary learning in face recognition. Proc. 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). San Francisco, CA, USA. 2010. 2691–2698.

17Jiang ZL, Lin Z, Davis LS. Learning a discriminative dictionary for sparse coding via label consistent K-SVD.Proc. 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Providence, RI, USA. 2011.1697–1704.

18Lee H, Battle A, Raina R, et al. Efficient sparse coding algorithms. Advances in Neural Information ProcessingSystems 19, Proc. Twentieth Annual Conference on Neural Information Processing Systems, Vancouver. British Columbia Canada. 2006. 801–808.

19Wang JJ, Yang JC, Yu K, et al. Locality-constrained linear coding for image classification. Proc. 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). San Francisco, CA, USA. 2010. 3360–3367.

20Yang M, Zhang L, Feng XC, et al. Fisher discrimination dictionary learning for sparse representation. Proc. 2011 IEEE International Conference on Computer Vision (ICCV).Barcelona, Spain. 2011. 543–550.

21Candès EJ, Li XD, Ma Y, et al. Robust principal component analysis?. Journal of the ACM (JACM), 2011, 58(3): 11.

22Candes EJ, Plan Y. Matrix completion with noise. Proc.IEEE, 2010, 98(6): 925–936. [doi: 10.1109/JPROC.2009.2035722]

23Candès EJ, Recht B. Exact matrix completion via convex optimization. Foundations of Computational Mathematics,2009, 9(6): 717–772. [doi: 10.1007/s10208-009-9045-5]

24Wright J, Ganesh A, Rao S, et al. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. Advances in Neural Information Processing Systems. Vancouver, British Columbia, Canada. 2009. 2080–2088.

25Cui XY, Huang JZ, Zhang ST, et al. Background subtraction using low rank and group sparsity constraints. Fitzgibbon A,Lazebnik S, Perona P, et al. Computer Vision-ECCV 2012.Berlin Heidelberg, Germany. 2012. 612–625.

26Shen XH, Wu Y. A unified approach to salient object detection via low rank matrix recovery. Proc. 2012 IEEE Conference on Computer Vision and Pattern Recognition(CVPR). Providence, RI, USA. 2012. 853–860.

27Zhang TZ, Ghanem B, Liu S, et al. Low-rank sparse learning for robust visual tracking. Fitzgibbon A, Lazebnik S, Perona P, et al. Computer Vision-ECCV 2012. Berlin Heidelberg,Germany. 2012. 470–484.

28Chen CF, Wei CP, Wang YCF. Low-rank matrix recovery with structural incoherence for robust face recognition. Proc.2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Providence, RI, USA. 2012.2618–2625.

29Liu G, Lin Z, Yu Y. Robust subspace segmentation by lowrank representation. International Conference on Machine Learning. Haifa, Isreal. 2010. 663–670.

30Ma L, Wang CH, Xiao BH, et al. Sparse representation for face recognition based on discriminative low-rank dictionary learning. Proc. 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Providence, RI, USA.2012. 2586–2593.

31Li LY, Li S, Fu Y. Learning low-rank and discriminative dictionary for image classification. Image and Vision Computing, 2014, 32(10): 814–823. [doi: 10.1016/j.imavis.2014.02.007]

32Zhang Y, Jiang ZL, Davis LS. Learning structured low-rank representations for image classification. Proc. 2013 IEEE Conference on Computer Vision and Pattern Recognition.Portland, OR, USA. 2013. 676–683.

33Nguyen H, Yang WK, Sheng BY, et al. Discriminative lowrank dictionary learning for face recognition. Neurocomputing, 2016, 173: 541–551. [doi: 10.1016/j.neucom.2015.07.031]

34Rodriguez F, Sapiro G. Sparse representations for image classification: Learning discriminative and reconstructive non-parametric dictionaries. Minnesota, USA: University of Minnesota. 2008.

35Pham DS, Venkatesh S. Joint learning and dictionary construction for pattern recognition. Proc. IEEE Conference on Computer Vision and Pattern Recognition, 2008. CVPR 2008. Anchorage, AK, USA. 2008. 1–8.

36Mairal J, Ponce J, Sapiro G, et al. Supervised dictionary learning. Advances in Neural Information Processing Systems. Vancouver, British Columbia, Canada. 2009.1033–1040.

37Yang JC, Yu K, Huang T. Supervised translation-invariant sparse coding. Proc. 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). San Francisco, CA,USA. 2010. 3517–3524.

38Lin ZC, Chen MM, Ma Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv preprint arXiv:1009.5055, 2010.

39Lee KC, Ho J, Kriegman DJ. Acquiring linear subspaces for face recognition under variable lighting. IEEE Trans. Pattern Analysis and Machine Intelligence, 2005, 27(5): 684–698.[doi: 10.1109/TPAMI.2005.92]

40Graham DB, Allinson NM. Characterising virtual eigensignatures for general purpose face recognition.Wechsler H, Phillips PJ, Bruce V, et al. Face Recognition.Berlin Heidelberg, Germany. 1998. 446–456.

41Martinez AM, Benavente R. The AR face database.Technical Report 24. Barcelona, Spain: CVC, 1998.

Discriminative Low-Rank Dictionary Leaning For Face Recognition

LI Run-Lin
(College of Computer &Communication Engineering, China University of Petroleum, Qingdao 266580, China)

Face recognition is active in the field of computer vision and pattern recognition and has extremely wide-spread application prospect. However, the problem that both training images and testing images are corrupted is not well solved in face recognition task. To address such a problem, this paper proposes a novel Discriminative Low-Rank Dictionary Learning for Low-Rank Sparse Representation algorithm (DLRD_LRSR) aiming to learn a pure dictionary. We suggest each sub dictionary and sparse representation be low-rank for reducing the effect of noise in training samples and introduce a novel discriminative reconstruction error term to make the coefficient more discriminating. We demonstrate the effectiveness of our approach on three public face datasets. Our method is more effective and robust than the previous competitive dictionary learning method.

dictionary learning; low-rank matrix recovery; face recognition; ALM

利润霖.面向人脸识别的判别低秩字典学习算法.计算机系统应用,2017,26(7):137–145. http://www.c-s-a.org.cn/1003-3254/5917.html

2016-11-18; 收到修改稿时间: 2017-01-16