基于动态调整的多目标粒子群优化算法①

李克文, 张永哲

(中国石油大学(华东) 计算机与通信工程学院, 青岛 266580)

基于动态调整的多目标粒子群优化算法①

李克文, 张永哲

(中国石油大学(华东) 计算机与通信工程学院, 青岛 266580)

为了改善多目标粒子群优化算法生成的最终Pareto前端的多样性和收敛性, 提出了一种针对多目标粒子群算法进化状态的检测机制. 通过对外部Pareto解集的更新情况进行检测, 进而评估算法的进化状态, 获取反馈信息来动态调整进化策略, 使得算法在进化过程中兼顾近似Pareto前端的多样性和收敛性. 最后, 在ZDT系列测试函数中,将本文算法与其他4种对等算法比较, 证明了本文算法生成的最终Pareto前端在多样性和收敛性上均有显著的优势.

多目标优化; 粒子群算法; 反馈信息; 进化状态

1 引言

粒子群算法(Particle swarm optimization, PSO)[1]最早由Kennedy和Eberhart在1995年提出. 自Coello等人[2]在2002年提出采用粒子群算法求解多目标优化问题后, 多目标进化领域中的许多成功经验被借鉴到多目标粒子群优化算法中, 并出现了大量的成果[3-8]. 文献[9]提出的agMOPSO算法采用自适应网格的方法评估Pareto最优解的个体密度, 进而剔除质量较差的粒子; 文献[10]提出的pdMOPSO算法采用ROUND、RANDOM以及PROB三种策略来选取全局最优解, 这些策略有利于提高Pareto前端的多样性, 但不易收敛到真实的Pareto前端. 文献[11]提出的σMOPSO算法通过比较目标向量之间的σ值来选取全局最优解, 这种策略会导致算法容易早熟, 陷入局部极值. 文献此外, 还有小生境[12]、最大最小适应度[13]策略等. 这些多目标粒子群优化算法忽略了一个问题: 如何平衡算法在进化过程中的开发和开采?过度的开发会影响最终的优化精度, 过度的开采会陷入局部极值. 当前所存在的多目标粒子群优化算法缺乏对进化状态的动态检测机制,难以获取反馈信息来决定算法在何时采用何种进化策略. 基于此, 本文提出了一种基于动态调整的多目标粒子群优化算法进化策略, 通过检测外部档案中解的更新情况评估算法的进化状态, 获取反馈信息来动态调整算法的进化策略, 使得算法在进化过程中能够平衡开发和开采, 兼顾到最终解集的多样性和收敛性.

本文第二节介绍多目标优化问题和粒子群优化算法的基本概念, 第三节介绍通过检测外部档案的更新情况来评估算法进化状态的方法, 第四节描述本文提出的动态调整策略和算法的完整流程, 第五节分析对比试验结果, 第六节给出全文结论.

2 基本概念

2.1 多目标优化问题

对于最小化无约束连续多目标优化问题, 如公式(1)所示:

Pareto占优: 对于任意两个向量称u占优v,或者v被u占优, 当且仅当:

Pareto最优解: 一个解∗被称为Pareto最优解或Pareto非占优解, 当且仅当:

Pareto最优解集: 所有Pareto最优解的集合PS被称作Pareto最优解集.

2.2 粒子群优化算法

在粒子群优化算法中, 个体i没有质量, 在进化过程中其位置和速度按照公式(5)更新.在公式(5)中, vi表示速度向量, xi表示位置向量, t表示迭代次数, ω≥0表示惯性权重系数, c1, c2≥0表示加速系数,r1和r2是[0, 1]上均匀分布的随机数, pBesti表示第i个粒子的个体最优解, gBest表示群体的全局最优解.

3 进化状态评估检测

根据外部档案的更新情形, 对算法的进化状态做如下定义:

停滞状态: 在第t次迭代过程中, 算法产生的新解被拒绝进入外部集, 则称算法在第t次迭代中处于停滞状态.

多样化状态: 在第t次迭代过程中, 算法产生的新解替换了外部集中适应度较差的旧解, 则称算法在第t次迭代中处于多样化状态.

收敛状态: 在第t次迭代过程中, 如果算法产生的近似Pareto前端与真实的Pareto前端发生了目标空间上的距离逼近, 则称算法在第t次迭代过程中处于收敛状态.

种群在一次的迭代过程中可产生N个新解, 不同性质的新解可能使得算法处于不同的进化状态. 因此, 需要从宏观上来判断算法所处的进化状态. 下面举例说明如何判断算法的进化状态.

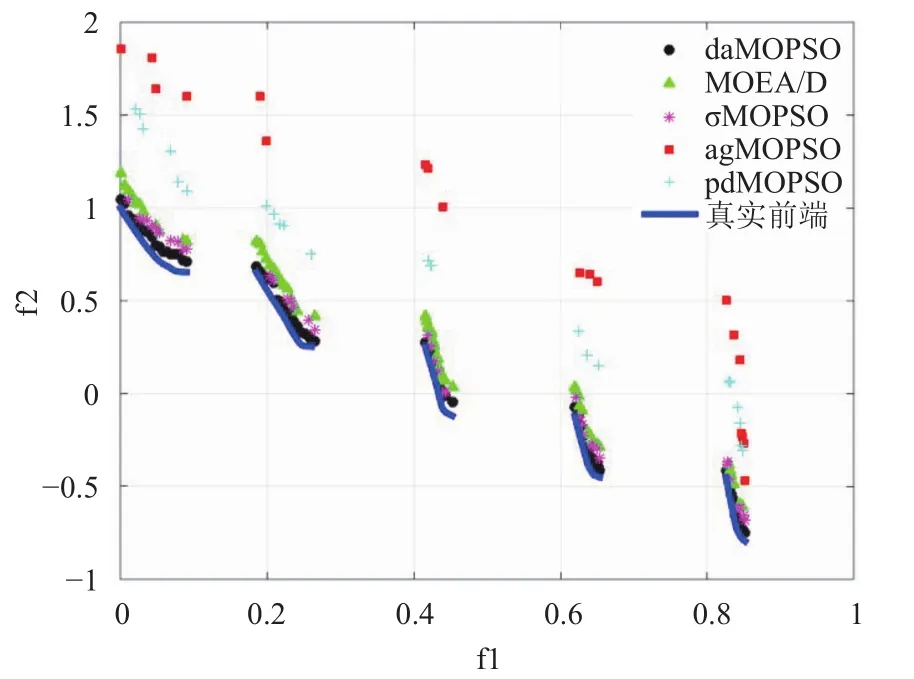
假设在第t次迭代中, 算法产生m个新解X1, X2,…Xm进入到外部集. 对于某一个新解Xi(1

称算法在宏观上朝着多样化状态发展, 当且仅当:

称算法在宏观上朝着收敛状态发展, 当且仅当:

称算法在宏观上平衡发展, 当且仅当:

其中, v为阈值, v取值过大, 会使得算法在进化过程中陷入局部最优, v取值过小, 会使得算法在评估进化状态时出现状态抖动(在多样化状态和收敛状态之间频繁转换). 在总结多次试验中的阈值取值后, v的取值范围宜为此次迭代过程中产生的新解个数的5%-10%.

4 基于动态调整的多目标粒子群优化算法

4.1 全局最优解选择策略

为了使算法在进化过程中兼顾收敛性和多样性,需要从外部档案中选取代表收敛性和多样性的Pareto最优解作为全局最优解, 引导算法种群平衡开采和开发过程. 通常, 收敛性和多样性是相互冲突的, 因此, 需要选取不同的度量标准来评估外部档案Pareto解集的收敛性和多样性.

外部档案中的Pareto最优解的个体密度可以作为多样性指标, 个体密度最小的Pareto解作为全局最优解引导种群在目标空间的稀疏区域进行探索, 可增加Pareto前端的多样性. 在自适应网格中, Pareto最优解的个体密度den(Xi)定义为同Xi格坐标相同的的Pareto最优解的个数.在自适应网格中, 第k个Pareto最优解的格坐标分量计算方式如公式(9)所示:

其中, pk,m表示第k个Pareto最优解在第m个目标分量上的值, m=1, 2, …, M, M表示目标个数, k=1, 2, …, K, K表示当前迭代过程中外部Pareto解集中的解个数, fk,m表示该最优解在第m个目标分量上的取值,表示目前第m个目标分量上的最小值和最大值. 为向上取整. 这里的目标维度分割数K不需要事先取值, 不依赖用户对MOPSO问题的相关先验知识, 将随着外部Pareto解集中的解个数变化而变化.

为了选取合适的收敛性指标, 在这里借鉴参考文献[14]提出的格占优和格占优强度并稍作修改, 提出G-占优和G-占优强度两个定义.

G-占优: 假设Gx,m和Gy,m(m=1, 2, …M, M为目标个数)是外部档案中任意两个解X, Y在自适应网格中的格坐标, 称XG-占优Y, 当且仅当:

记作.

G-占优强度: 对于一个Pareto最优解X, 其G-占优强度是它在自适应网格中G-占优外部档案A中其它Pareto最优解的数目, 即:

G-占优强度反应了一个Pareto最优解逼近真实Pareto前端的程度, 因此可以作为外部档案的收敛性指标.

根据以上分析, 可得出全局最优解选择策略:

输入: 1) 外部档案A和目标个数M;

2) 算法所处的进化状态Status∈{停滞状态, 多样化状态, 收敛状态}.

输出: 全局最优解gBest.

步1: 遍历A中的所有Pareto最优解, 分别计算其个体密度和G-占优强度;

步2: 个体密度集合D中升序存放Pareto最优解, G-占优强度集合G中降序存放Pareto最优解, 全局最优解候选集合C置空;

步3: 如果进化状态为停滞状态或平衡进化,C=TOP(D, |C|/2)∪TOP(G, |C|/2);

步4: 如果进化状态为多样化状态, C=TOP(D,|C|/2--)∪TOP(G, |C|/2++);

步5: 如果进化状态为收敛状态, C=TOP(D,|C|/2++)∪TOP(G, |C|/2--);

步6: gBest=Random(C).

注释: (1) TOP(P, n)表示从有序集合P中返回最前面n个成员;

(2) n++(或n--)表示每次迭代中n加1(减1);

(3) Random(Q)表示从集合Q中随机选择一个成员.

4.2 个体最优解选择策略

在个体最优解选择策略方面, 为了使算法在选择个体最优解时最大化地保留个体最优解选择的多样性,本文提出的算法将为个体最优解维护一个外部档案来存储个体最优解, 同时为了降低算法的复杂度, 将其大小设为全局最优解外部档案的1/6, 为了保证个体最优解的变化能够跟踪全局最优解的快速变化, 在个体选择最优解时将选择距离全局最优解最近(已经通过公式(9)确定)的粒子作为个体最优解.

4.3 局部极值扰动策略

为了改善粒子群算法在多目标优化中易陷入局部最优的不足, 本文将采用文献[15]提出的精英学习策略(Elitism Learning Strategy, ELS)来辅助算法跳出局部极值. 当算法陷入停滞状态的时候在全局最优解候选集合C中随机选择某个成员作为参与学习的精英粒子, 学习率lp的计算方法如公式(12)所示:

在公式(12)中, Stepl表示精英学习率的步长, 其大小为最大学习率和最小学习率的区间长度除以迭代次数, 在本文算法中, 最大学习率和最小学习率分别为0.5和0, 算法开始时设定精英学习率为最大值, 扰动幅度参考文献[15], 如公式(13)所示:

在公式(13)中, Xd表示精英学习粒子被随机选中的第d个决策变量,分别为第d个决策变量的最大值和最小值, r为[0, 1]上的随机数, Gaussian(0, r2)是均值为0、方差为r的高斯函数.

4.4 算法整体流程

输入: 1) 多目标待优化问题;

2) 具有D个决策变量的搜索空间;

3) 初始化相关参数: 外部档案的最容量K, 最大迭代次数Tmax, 种群数量N.

输出: 外部档案中的近似Pareto最优解集.

步1: 初始化种群

(1) 迭代次数设置为0;

(2) 在搜索空间中均匀随机生成N个粒子;

(3) 根据多目标问题计算每个粒子的第m个目标函数值;

(4) 判断哪些粒子可以进入外部档案.

步2: 迭代次数加1

步3: 评估进化环境

(1) 根据公式(6)(7)(8)判定算法的进化状态;

(2) 根据公式(9)和公式(11)计算外部档案中每个解的个体密度和G-占优强度.

步4: 调整算法的运动参数: 算法的学习因子设定为2.05, 惯性权重随着迭代次数从0.9线性下降到0.4.

步5: 更新种群

(1) 根据全局最优解选择策略和个体最优解选择策略选择选择全局最优解gBesti和个体最优解pBesti.

(2) 根据运动方程以及运动参数更新粒子的位置和速度;

(3) 如果算法陷入停滞状态, 将根据公式(12)所确定的学习率lp按照公式(13)对粒子进行局部极值扰动.

(4) 评估粒子的目标函数值;

(5) 根据全局最优解选择策略和个体最优解选择策略更新种群的个体最优解候选集和全局最优解候选集;

步6: 迭代终止条件(如果迭代次数大于预设定次数, 结束; 否则转步2).

5 实验及结果分析

为了验证本文提出的算法(daMOPSO), 本文在实验中选取了4种常用于比较多目标优化的对等算法, 包括agMOPSO[9], pdMOPSO[10], σMOPSO[11]及MOEA/D[16], 在对比实验中, 将选取各对比算法的种群大小均设定为N=100, 外部档案规模均设定为K=100,算法的迭代次数均设定为T=300. 各对比算法的参数都按照各自的参考文献设置. daMOPSO的学习因子设置为2.05, 惯性权重随迭代次数从0.9线性下降到0.4, 阈值v取各迭代过程中产生的新解个数的6%. 各对比算法在所有的测试函数上都独立运行30次以降低随机影响.

为了评估本文提出的算法生成的近似Pareto前端的多样性和收敛性, 本文将采用反转世代距离(Inverted Generational Distance, IGD)[16]作为评估指标. 其计算方法如公式(14)所示:

本文选择ZDT1、ZDT2、ZDT3、ZDT4和ZDT6这组测试函数来测试各个算法的性能, ZDT5作为布尔函数, 需要二进制编码, 本文略去该测试函数. 获得的近似Pareto前端如图1至图5所示. σMOPSO在ZDT4测试中获得的Pareto前端和agMOPSO、σMOPSO、pdMOPSO在ZDT6测试中获得的Pareto前端质量太差, 在图中未表示.

图1 ZDT1的测试结果

图2 ZDT2的测试结果

图3 ZDT3的测试结果

图4 ZDT4的测试结果

表1给出了各个算法在独立运行30次后获得的IGD的平均值(mean)和方差值(std).

通过表1可以看出, daMOPSO在测试函数中取得的整体效果非常理想, 仅在ZDT4的测试中结果不如MOEA/D, ZDT4函数具有219个不同的局部Pareto最优前沿, 其中只有一个对应全局最优前沿, 这说明daMOPSO在在跳出局部最优时与MOEA/D相比略显不足.

图5 ZDT6的测试结果

表1 各个算法在5种测试函数中获得的IGD对比

与其它几种对等算法相比, 由于daMPSO在维护全局外部档案集的同时维护了一个个体外部档案集, 因此空间复杂度要大于其它几种对等算法, daMOPSO在每一次迭代中都会计算每一个最优解的个体密度和G-占优强度, 因此时间复杂度也略高于其它几种算法.

下一步笔者将会对daMOPSO的跳出局部最优能力以及降低时空复杂度进行探索提升. 总体来看, daMOPSO在处理这类优化问题时的能力要优于其它几种对比算法.

6 总结

基于动态调整的多目标粒子群优化算法(daMOPSO)通过检测外部档案的更新情况确认算法的进化状态,通过个体密度和G-占优强度来评价个体适应度, 并根据不同的进化状态动态调整算法的进化策略, 保证算法在进化过程中能够兼顾Pareto前端的多样性和收敛性. 选择了ZDT系列测试函数对daMOPSO算法进行了测试, 结果表明该算法在处理不同类型的Pareto前端时都表现出了比较优秀的性能.

1Kennedy J, Eberhart R. Particle swarm optimization. Proc. of IEEE International Conference on Neural Networks. Perth,WA, Australia. 1995. 1942–1948.

2Coello Coello CA, Lechuga MS. MOPSO: A proposal for multiple objective particle swarm optimization. Proc. of the 2002 Congress on Evolutionary Computation. Honolulu, HI,USA. 2002. 1051–1056.

3Maltese J, Ombuki-Berman B, Engelbrecht A. Co-operative vector-evaluated particle swarm optimization for multiobjective optimization. Proc. 2015 IEEE Symposium Series on Computational Intelligence. Cape Town, South Africa.2015. 1294–1301.

4Padhye N, Branke J, Mostaghim S. Empirical comparison of MOPSO methods—guide selection and diversity preservation. Proc. of IEEE Congress on Evolutionary Computation. Trondheim. 2009. 2516–2523.

5Dai C, Wang YP, Ye M. A new multi-objective particle swarm optimization algorithm based on decomposition.Information Sciences, 2015, 325: 541–557. [doi: 10.1016/j.ins.2015.07.018]

6Coelho LDS, Guerra FA, Leite JV. Multiobjective exponential particle swarm optimization approach applied to hysteresis parameters estimation. IEEE Trans. on Magnetics,2012, 48(2): 283–286. [doi: 10.1109/TMAG.2011.2172581]

7Moubayed NA, Petrovski A, McCall J. Clustering-based leaders’ selection in multi-objective particle swarm optimisation. Yin H, Wang W, Rayward-Smith V. Intelligent Data Engineering and Automated Learning-IDEAL 2011.Berlin, Heidelberg, Germany. 2011. 100–107.

8Zhou AM, Qu BY, Li H, et al. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm and Evolutionary Computation, 2011, 1(1): 32–49. [doi: 10.1016/j.swevo.2011.03.001]

9Coello CCA, Pulido GT, Lechuga MS. Handling multiple objectives with particle swarm optimization. IEEE Trans. on Evolutionary Computation, 2004, 8(3): 256–279. [doi:10.1109/TEVC.2004.826067]

10Alvarez-Benitez JE, Everson RM, Fieldsend JE. A MOPSO algorithm based exclusively on Pareto dominance concepts.Coello Coello CA, Hernández AA, Zitzler E. Evolutionary Multi-Criterion Optimization. Berlin, Heidelberg, Germany.2005. 459–473.

11Mostaghim S, Teich J. Strategies for finding good local guides in multi-objective particle swarm optimization(MOPSO). Proc. of the 2003 IEEE Swarm Intelligence Symposium. Indianapolis, IN, USA. 2003. 26–33.

12Zhao QL. The Research of the Niche particle swarm optimization based on self-adaptive radius technology. Proc.of Asia-Pacific Conference on Information Processing.Shenzhen, China. 2009. 97–100.

13徐佳, 李绍军, 王惠, 等. 基于最大最小适应度函数的多目标粒子群算法. 计算机与数字工程, 2006, 34(8): 31–34.

14胡旺, Yen GG, 张鑫. 基于Pareto熵的多目标粒子群优化算法. 软件学报, 2014, 25(5): 1025–1050.

15Zhan ZH, Zhang J, Li Y, et al. Adaptive particle swarm optimization. IEEE Trans. on Systems, Man, and Cybernetics, Part B (Cybernetics), 2009, 39(6): 1362–1381.[doi: 10.1109/TSMCB.2009.2015956]

16Zhang QF, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. on Evolutionary Computation, 2007, 11(6): 712–731. [doi: 10.1109/TEVC.2007.892759]

Multi Objective Particle Swarm Optimization Based on Dynamic Adjustment

LI Ke-Wen, ZHANG Yong-Zhe
(College of Computer and Communication Engineering, China University of Petroleum, Qingdao 266580, China)

To improve the diversity and convergence of Pareto front generated by multi objective particle swarm optimization, a detection mechanism for evolutionary state of multi objective particle swarm optimization is presented in this paper. The evolutionary state of the algorithm is assumed by detecting the updating situation of the external Pareto set to get the feedback information to adjust the evolutionary strategy of the algorithm dynamically. It enables the algorithm to take the diversity and convergence of the approximate Pareto front into account in the process of the evolution. Finally,the proposed algorithm shows a good performance compared with other four kinds of equivalence algorithms in the ZDT series test function.

multi objective optimization; particle swarm optimization; feedback information; evolutionary state

张永哲, E-mail: 864238735@qq.com

李克文,张永哲.基于动态调整的多目标粒子群优化算法.计算机系统应用,2017,26(7):161–166. http://www.c-s-a.org.cn/1003-3254/5820.html

山东省自然科学基金(ZR2013FL034)

2016-10-20; 收到修改稿时间: 2016-11-14