基于ARMA模型的工业电容退化状态研究方法①
2017-07-19陶耀东余骋远
张 峥, 陶耀东,2, 余骋远
1(中国科学院大学, 北京 100049)
2(中国科学院 沈阳计算技术研究所有限公司, 沈阳 110168)
基于ARMA模型的工业电容退化状态研究方法①
张 峥1, 陶耀东1,2, 余骋远1
1(中国科学院大学, 北京 100049)
2(中国科学院 沈阳计算技术研究所有限公司, 沈阳 110168)
随着中国制造2025计划的推广, 工业电源正处于高速发展期, 大型铝电解电容的需求越来越大. 电容的故障会令工业流水线中断, 产生极大的损失, 因此工业电容的寿命预测(RUL)具有重要意义. 本文通过对铝电解电容充电状态EIS频谱分析, 建立电容的状态的量化模型. 根据电容状态量化数据, 建立ARMA电容退化预测模型. 最后通过美国航天航空局的等效串联电阻EIS频谱数据集进行验证. 结果表明ARMA电容退化模型对铝电解电容的状态预测有很大的准确性.
工业铝电解电容; 退化预测模型; 剩余使用寿命; ARMA; PHM
在现代工业中, 铝电解电容器已成为关键的滤波元器件广泛地应用在电气系统中, 如航电设备的电源供应系统和机电制动器的电力驱动装置. 这些电容确保在高动态负载的条件下, 小规模的噪声不会干扰的整体系统的平稳运行. 但是, 它们始终以低可靠性著称,经常发生故障. 电容的故障或损毁常常会令高速运行的流水线突然停止, 使工业企业产生极大的损失. 因此对铝点解电容的剩余寿命预测成为工业电容故障诊断健康管理(PHM)的重要问题. 工业铝点解电容剩余寿命预测(RUL)是一个涵盖电化学、可靠性统计、机器学习、计算机等多领域的交叉的课题. 国外马里兰大学先进寿命周期工程中心(Center for Advanced Life Cycle Engineering)对剩余使用寿命(RUL)的研究处于世界领先地位[1,2]. NASA的卓越故障预测研究中心(Prognostics Center of Excellence, PCoE)的Jason Renwick等人大力研究铝电解电容的使用状态, 并提供多组开放数据集[3]. 美国辛辛那提大学的李杰团队对PHM系统的研究, 更系统地提出“数据驱动”的工业设备状态监测思想, 并取得一定成果[4].
1 铝点解电容性能退化评估预测模型
1.1 退化评估框架
在电容的退化状态分析与评估中, 始终存在三个关键问题: 选取合适的退化特征, 正确识别退化状态与建立退化预测模型[5]. 对于第一个问题, 浙江大学的马皓博士等人提出了对电容的等效串联电阻(ESR)模型的识别与推导可以表征电容器的状态[6]. 浙江大学的曹楚南、张鉴清等人运用电化学阻抗谱(EIS)来描述ESR的内部状态[7]. 对于第二个问题, NASA机构的Jason Renwick等人通过对EIS的分析, 了解得到同一个周期内阻抗的实部与虚部变化速度可以表征电容器的ESR系统的退化状态[8]. 对于最后一个问题, 西安电子科技大学的翟利波提出基于时间序列分析的剩余寿命预测模型[9].
本文采用的工业铝电解电容性能评估解决方案下列流程图1所示. 利用电化学知识提取根据EIS测量的有效数据, 将与电容状态有关数据拟合成铝电解电容状态标识模型, 最后研究不同充电周期的阻抗曲线的关系, 给出一种工业电容器的退化状态分析与评估方案.

图1 工业铝电解电容性能评估解决方案
1.2 等效串联电路的EIS频谱数据
工业电容设备不宜轻易拆解, 其内部结构未知犹如一个黑箱, 但这个黑箱通常有一个输入端与一个输出端. 为了研究其内部结构, 通常对其输入端施加一个足以不干扰内部运行的小规模电势(或电流)扰动信号,使电极系统产生该干扰信号的的响应. 假设有一个物理系统M, 如果进行一个角速度为ω的正弦波电信号的扰动. 当X为扰动信号, G为由M自身特性决定的频响函数, Y为响应信号. 则XY之间的关系为:

如果X信号为正弦波电流, Y为正弦波电压, 则称G为M的阻抗, 针对于电容电阻电路的G是一个有具有实部与虚部的复数. 实部表示电阻的特性, 虚部表示电容的特性. 使用EIS方法测量的铝电解电容等效串联电阻的阻抗, 可以间接描述电容器的退化状态.
1.3 基于最小化误差思想的多项式拟合
用n阶多项式函数逼近一个曲线的拟合方式称为多项式拟合. 多项式拟合的优点有很多, 最重突出的就是更容易求出微分与积分, 因而更适用于强调变化率的研究. 目前, 流行的拟合算法很多, 例如拉格朗日插值法、最小二乘法等. 拉格朗日插值法本身要求插值函数在给定点处的函数值完全符合, 而最小二乘法要求给定点偏差平方和为最小值, 并不要求一定通过给定点. 前者会因过分强调函数过定点而造成过拟合, 适合拟寻找生成函数, 不适合探求拟合规律. 同时, 带岭回归最小二乘法可以在一定程度上防止过拟合的发生.所以本文选取以最小二乘法为基础的岭回归方法做多项式拟合[10].
设一个超定方程组如公式(方程组的未知数个数少于方程个数):
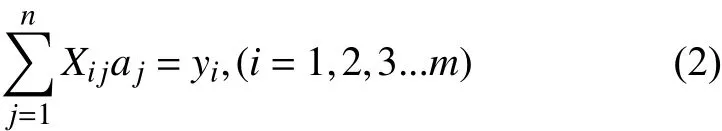
其中m代表有m个等式, n代表有n个未知参数a, m>n; 将其进行向量化后为:
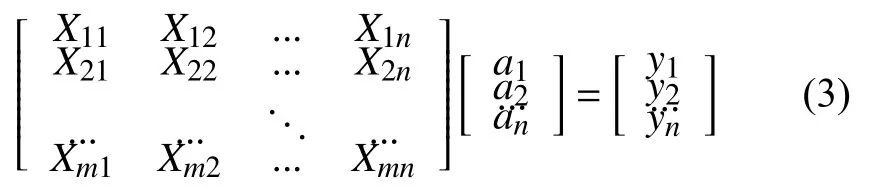
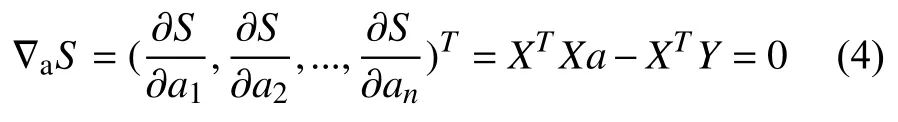
假设XTX可逆, 则可得. 但XTX是个半正定矩阵, 不一定可逆. 所以如果不可逆, 可以在XTX加上一个小的正定惩罚项. 令其变成正定可逆矩阵求逆形式, 即, 就可以粗略参数值,这种求解方法叫带岭回归的最小二乘法.
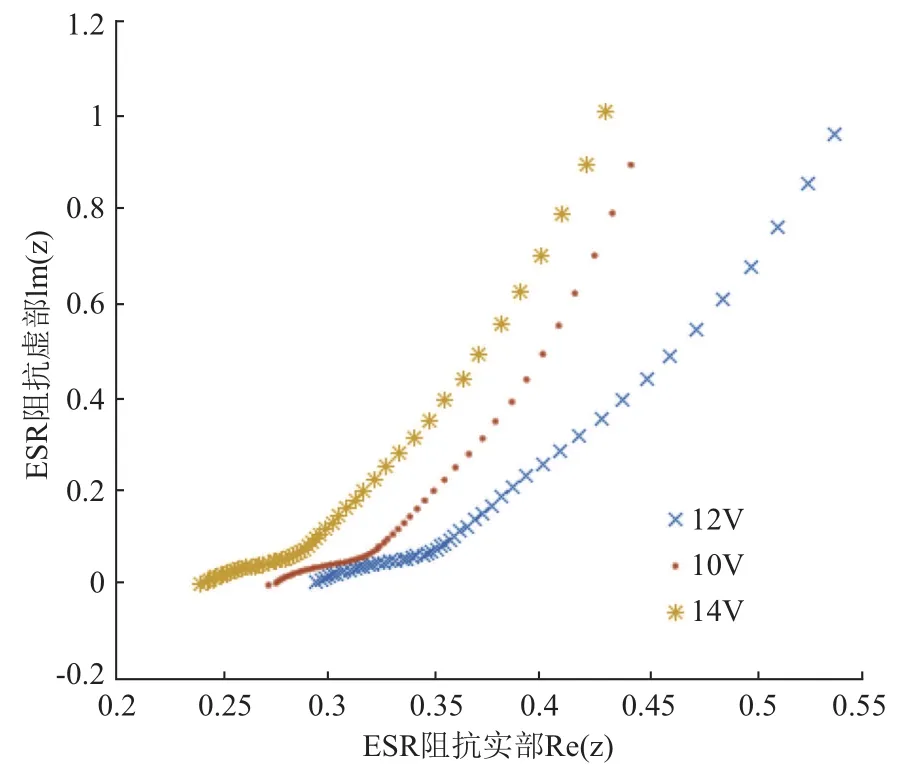
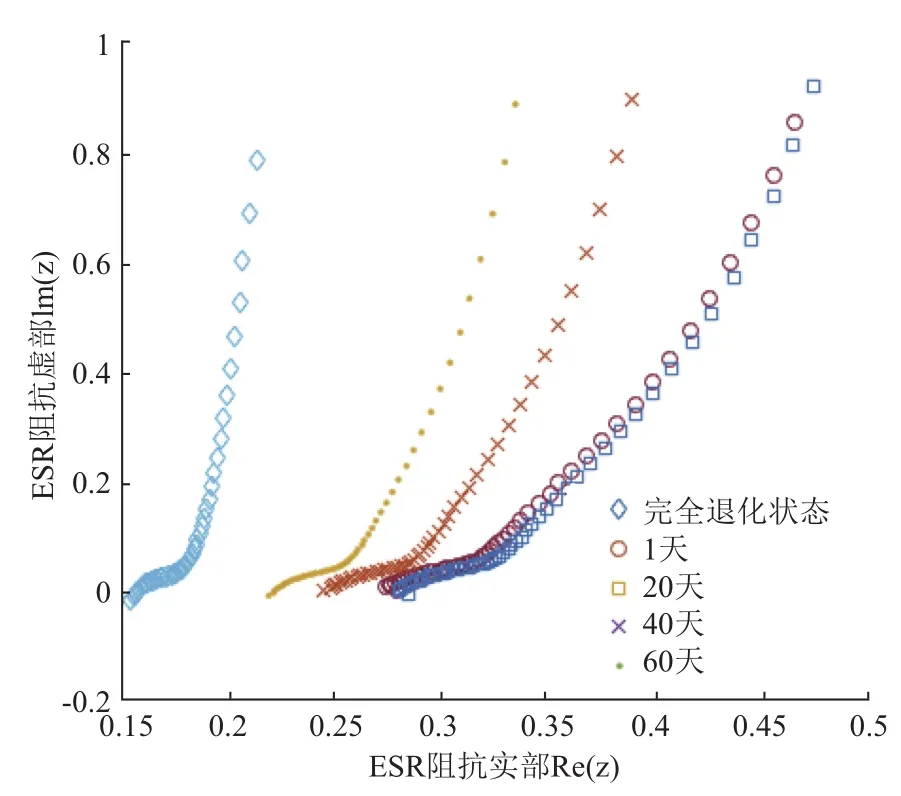
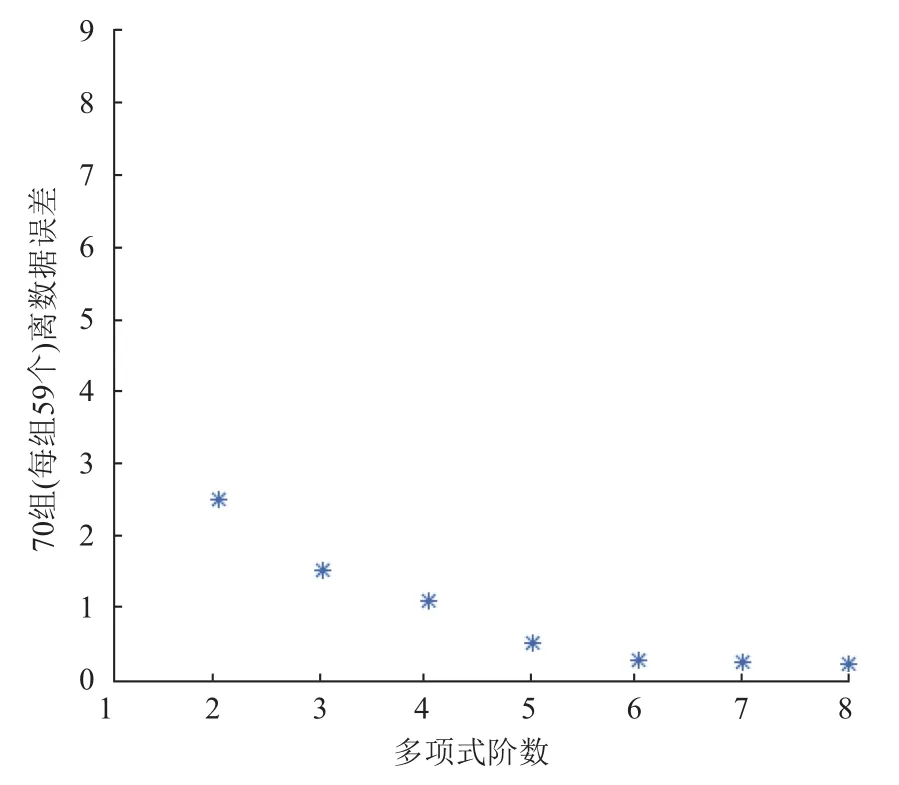
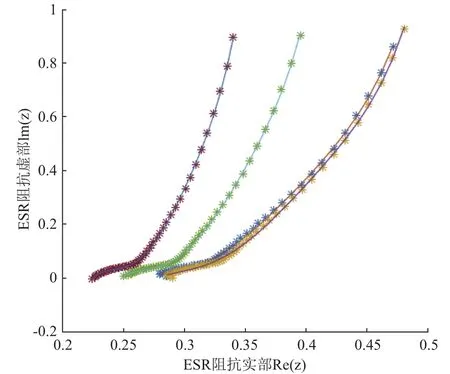
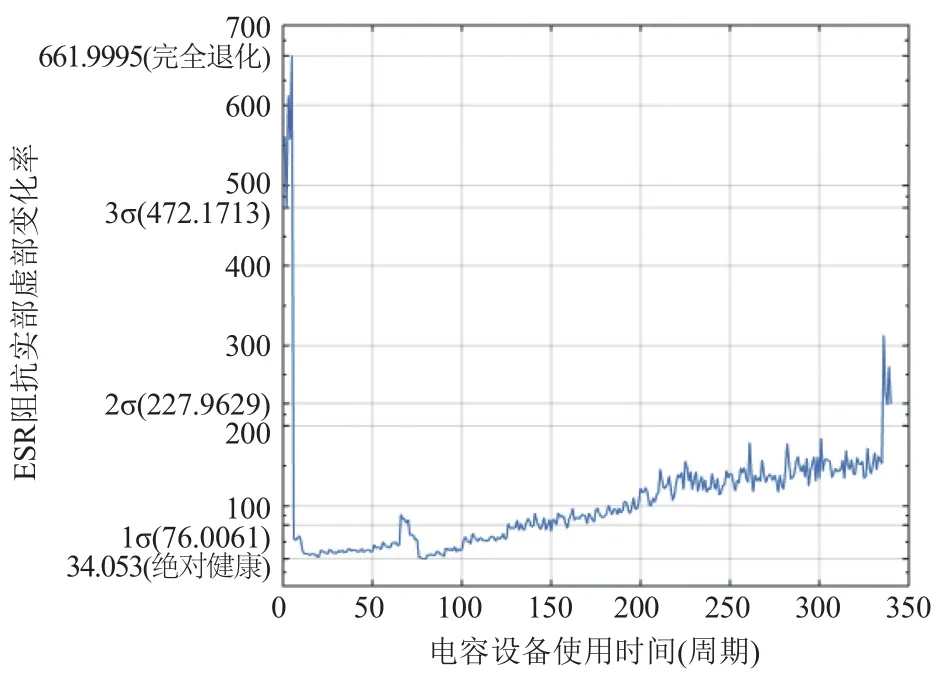
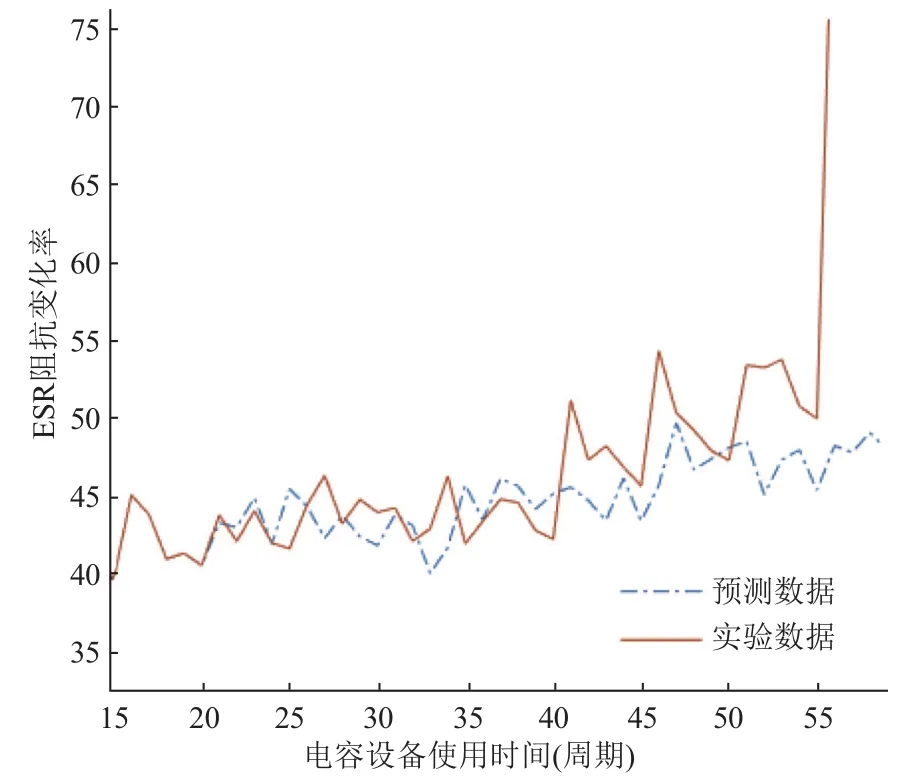
多项式拟合中阶数越大越准确, 但是阶数越大过度拟合的现象可能越来越严重. 虽然岭回归可以在一定程度上防止过拟合事件, 但为了进一步防止过度拟合的发生, 需要人为地做几条规定: 第一, 限定最大阶数k必须满足k 1.4 工业电容的退化状态评估 在表征电容退化的阻抗变化率选定后, 即可量化设备退化状态. 状态的量化往往遵循以下两个原则: 第一, 确定量化值的上线与下线; 第二, 确定状态单位的刻度. 需要说明的是量化后的值不一定是可数的. 数值的仅仅标识状态, 大小比较无实际意义. 西格玛原则来源于质量管理学. 西格玛即希腊字母“σ”, 在统计学上有标准差的意思. N西格玛原则的意思为“N倍标准差”. 西格玛原则由于将质量明确的量化而在工业生产中广泛地使用[12]. 在退化的评估模型中,不同水平的西格玛原则数据可以标识不同级别的工业设备. 根据这些状态标识可以更好地表现出设备当前的健康状态. 表1 基于西格玛原则与电容运行状态标识 1.5 工业电容的退化状态评估 工业电容状态数据往往以时间维度的方式展现出来. 对大规模的时间维度的数据分析, 往往使用时间序列模型方法[13]. 时间序列分析是根据系统观测得到的时间序列数据, 通过曲线拟合和参数估计来建立数学模型的理论和方法. 目前以ARMA模型最为通用. 1.5.1 ARMA的时间序列模型 时间序列是指按时间顺序排列的一系列被观测的数据, 其信息(观测值)按固定的时间间隔采样.ARMA模型常用于带时间标签的工业状态预测[14,15]. 经采取的工业电容运行数据皆带有时间标签, 单位以充电周期计算. 所以本文利用ARMA算法解决工业电容的状态预测方案. ARMA时间序列模型为常用的线性回归时间序列预测模型, 由自回归模型AR(Auto-regressive)与滑动平均模型MA(Moving-Average )混合构成. 对于平稳、正态、零均值的时间序列{xi}, 如果序列与自身的过去n个状态存在线性关系, 那么称为n阶自回归模型, 记为AR(n)模型: 如果不考虑误差, 那么AR模型可以直接解决大部分问题. 如果考虑噪声误差, 考虑到序列对自身各时刻进入系统噪声存在记忆, 称为m阶滑动平均模型, 记为MA(m)模型: ARMA模型的就是将AR与MA模型组合起来. 相应地ARMA(n, m)就是AR(n)与MR(m)两模型的整合,数学描述为: n, m分别是自回归部分和滑动平均部分的阶次. 1.5.2 基于AIC信息准则的定阶方法[16] AIC信息准则方法是利用似然函数估计值最大原则来估计模型参数, 由于ARMA模型的阶数估计与参数估计互为条件, 需要固定ARMA(n, m)模型的一组阶数, 之后使用ARMA(n, m)模型的自回归逼近法求得白噪声的估计方差, 最后计算AIC价值函数: 其中k为自回归模型阶, j为滑动平均模型阶数, 为拟合残差平方和. 在模型阶数较小时, 拟合残差平方变化波动较大, 对价值函数影响较大, 当阶数达到一定阈值时,拟合残差变化波动变小, 那么模型阶数的影响变大. 设定ARMA模型的阶数上限为log N , 如果: 1.5.3 时间序列的平稳化预处理[17] 根据时间序列要求, 输入数据必须为平稳随机序列, 数据的统计特性与时间起点无关且均值为零. 而实际应用中, 随机序列大多不稳定, 呈现出极大的趋势性.可以进行序列差分的方式分离出趋势性特征, 如公式(10): 然后再采用时间序列方法进行将差分序列作为新的序列, 若还存在非平稳成分, 可多次差分直到序列平稳. 2.1 数据集说明与特征选择 本文基于等效串联电阻的EIS测得的阻抗来实现电容健康状态的评估. 为测试算法的有效性, 我们选择NASA Capacitor Electrical Stress Data Set. 三组八个铝电解电容器被以100 mHz(50%工作周期)的频率不断地充放电. 每组分别为10 V, 12 V, 和14 V电容设备的测量结果. 使用SP 150生物型恒电位仪对其进行电化学阻抗谱(EIS)测量. 每个数据集的开始部分都描述了一个快要被换掉的老电容器的工作数据, 运行5个工作周期后, 由于电容损耗严重而更换了一新电容. 我们可以将前五个工作周期视为损耗周期, 而第六个周期视为电容新周期进行分析. 新电容在新周期的初期会存在一定时间不稳定的状态, 所以做电容状态预测时从运行稳定的第十一周期开始. 为了数据完整性, 在初期量化评估时, 前十周期状态也考虑在内. 如图2,10 V、12 V、14 V三组电容设备的EIS数据记录. 在其中随机选取一个充电周期, 将实部与虚部建立坐标系. 图2中横轴代表EIS测量的阻抗值的实部, 纵轴代表阻抗值的虚部. 从中发现两个结论: 第一, 在同一充电周期中, 阻抗的实部与虚部变化成正相关, 适合拟合成多项式曲线进行研究, 并且伴随着充电阻抗的实部越大; 第二, 不同容量的电容在同一充电周期的表现大致相同, 可以使用相同的方案研究. 由于设备退化评估与具体电压数值没关系, 本文专注于电容量为12 V电容器设备的变化情况. 图3为12 V电容设备在不同使用时间测得的阻抗实部与虚部. 最左边的曲线为严重退化电容器的最后时刻数据, 这个数据作为设备退化的对照, 虽然此时电容没有完全坏掉, 但理论上可以将这样的状态视为电容设备完全退化状态. 图3右边的数据是新电容使用时间不久的状态. 在20天内电容器的阻抗数据还相对稳定, 但随着电容的不断充放电, 阻抗数据变化越来越明显. 短期使用的数据差异不大, 同理可将开始的状态视为设备健康状态. 2.2 电容退化状态的评估模型 将同周期的离散数据进行多项式曲线拟合, 首先要解决的问题是多项式的阶数判定. 这里用最小误差法定阶. 根据1.3中防止多项式过度拟合的原则, 每组59个离散数据, 可知n的最大值为7. 图4即为n取不同值时, 多项式拟合方程与实际值的误差. 可知n=5或6时取“肘点”. 但当n=6时, 拟合阶数过大, 阶数扩大而消除的误差反而较少, 故选取n为5. 多项式阶数确定之后, 可以直接用最小二乘法拟合, 并在n组测试集中随机抽取四组数据, 用来测验其拟合效果. 如图5, 图中的离散点就是选取的测试点, 曲线就是拟合的结果. 可知五阶多项式拟合下的阻抗实部-虚部函数能够区分相近的点集合, 误差较小, 结果令人满意. 图2 10 V, 12 V, 14 V三组电容设备的EIS数据记录 图3 电容的退化状态与阻抗曲线的关系 根据数据集, 按时间顺序依次求出每个充电周期曲线的导函数平均变化率. (如图6)最左边的部分记录着上一个接近换掉的电容状态, 可以理论上视为最终退化状态; 紧接着的记录是新电容的状态, 可视为初始健康状态. 再根据质量控制的西格玛原则, 电容设备的退化状态的量化结束. 在测试集中抽取一些数据, 表2即为这些退化状态的量化结果. 图4 多项式拟合阶数选择 图5 五阶多项式拟合结果测试 2.3 电容退化状态的预测模型 为确定ARMA模型的参数, 可以利用AIC准则进行确定. 如图7显示的是当前实验状态设置为第20个工作周期时短期预测效果, 后面的周期预测状况. 点划线为预测值, 直线为实际值. 当做短期预测15-20个周期(即第20到第40周期)时, 误差很不大, 平均预测误差为1.8864. 但20-35个周期(即第40到第55周期)的预测平均误差变为3.9765. 推测原因是在第40与第55周期时, 设备发生外力引起的扰动. 预测效果虽然没有马上产生变化, 但随后进行了反应. 之后的预测与实际值相差更悬殊了. 可知ARMA模型对短期预测精度较好, 长期预测精度较差. 图6 各个充电周期曲线的导函数平均变化率 图7 电容状态值预测与实际值 本文针对工业电容的运行特性提出了一整套评估方案, 并通过实验分析进行验证, 得到以下结论: 首先, 根据电容的等效串联电阻测量的EIS频谱的研究, 找到了一种基于ESR阻抗数据的电容健康状态量化方法. 这套方法可以将工业电容的健康值映射到100(绝对健康)到0(绝对退化)的区间上. 为后面的电容健康状态可视化、模型预测等操作提供了数据前提. 其次, 将质量管理学中的六西格玛原则迁移到工业控制数据分析中, 将连续变量离散化, 转变为三级健康状态(优良, 有退化, 退化严重). 如表2, 经工业电容数据的验证, 该方法有很直观的表现结果. 最后, ARMA模型可以预测工业电容的未来健康状态. 如图7, 根据电容状态量化数据建立的ARMA健康状态预测模型, 在大约15-20个充放电周期内有比较准确的预测效果, 20个充放电周期以后. 由于工业电容在实际运行中不可预知的因素(如负载突然增高, 高强度充放电等), 健康模型的长期预测效果较差. 1Hess A, Calvello G, Frith P, et al. Challenges, issues, and lessons learned chasing the “Big P”: Real predictive prognostics part 2. Proc. 2006 IEEE Aerospace Conference.Big Sky, Montana, USA. 2006. 1–19. 2Pecht MG. Prognostics and Health Management of Electronics. Hoboken, NJ. USA: John Wiley & Sons, Ltd., 2008. 3Celaya J, Kulkarni C, Biswas G, et al. Towards a modelbased prognostics methodology for electrolytic capacitors: A case study based on electrical overstress accelerated aging.International Journal of Prognostics and Health Management,2012, 3(2): 1–19. 4Lee J, Wu FJ, Zhao WY, et al. Prognostics and health management design for rotary machinery systems-reviews,methodology and applications. Mechanical Systems and Signal Processing, 2014, 42(1-2): 314–334. [doi: 10.1016/j.ymssp.2013.06.004] 5洪晟, 尉麒栋. 基于WNN的锂电池循环寿命预测. 计算机测量与控制, 2013, 21(8): 2146–2148. 6马皓, 王林国. 铝电解电容器退化分析与故障预诊断. 电力系统自动化, 2005, 29(15): 68–72, 99. [doi: 10.3321/j.issn:1000-1026.2005.15.014] 7曹楚南, 张鉴清. 电化学阻抗谱导论. 北京: 科学出版社,2002: 1–36. 8Renwick J, Kulkarni C, Celaya J. Analysis of electrolytic capacitor degradation under electrical overstress for prognostic studies. Proc. Annual Conference of the Prognostics and Health Management Society. Coronado CA,USA. 2015. 9翟利波. 基于时间序列分析的剩余寿命预测模型[硕士学位论文]. 西安: 西安电子科技大学, 2014. 10丁克良, 沈云中, 欧吉坤. 整体最小二乘法直线拟合. 辽宁工程技术大学学报(自然科学版), 2010, 29(1): 44–47. 11周志华. 机器学习. 北京: 清华大学出版社, 2016. 23–46. 12马迎新, 王军, 蔡勇, 等. 精益六西格玛在提升电力设备管理中的应用. 中国市场, 2012, (36): 21–24. [doi: 10.3969/j.issn.1005-6432.2012.36.008] 13苏卫星, 朱云龙, 胡琨元, 等. 基于模型的过程工业时间序列异常值检测方法. 仪器仪表学报, 2012, 33(9): 2080–2087. 14李瑞莹, 康锐. 基于ARMA模型的故障率预测方法研究. 系统工程与电子技术, 2008, 30(8): 1588–1591. 15谭赟. 时间序列分析模型构建与MATLAB实现. 科技资讯,2009, (26): 253–254. [doi: 10.3969/j.issn.1672-3791.2009.26.206] 16王世明, 李永乐. ARMA模型在浮标压力测量误差问题中的研究. 计算机测量与控制, 2010, 18(9): 2054–2056. 17潘迪夫, 刘辉, 李燕飞. 基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型. 电网技术, 2008, 32(7):82–86. Research on Degradation Study of Industrial Capacity Based on ARMA Model ZHANG Zheng1, TAO Yao-Dong1,2, YU Cheng-Yuan1 1(University of Chinese Academy of Sciences, Beijing 100049, China) With the promotion of “Made in China 2025”, the supply in industrial power is in a growing demand for large aluminum electrolytic capacitors. Capacitor failure can interrupt the industrial assembly line, causing a great loss. The prediction of RUL (Remaining Useful Life) of industrial capacitors is hence very important. In this paper, based on the analysis of the EIS of the aluminum electrolytic capacitor, a quantitative model of the state of the capacitor is established.Based on the quantitative data, the degradation prediction model of ARMA capacitor degradation is established. Finally,the equivalent series resistance EIS spectrum data set was verified by NASA. The results show that the short term ARMA capacitor degradation model is accurate in the prediction of the state of aluminum electrolytic capacitors. aluminum electrolytic capacitor; degradation prediction model; remaining useful life; ARMA; PHM 张峥,陶耀东,余骋远.基于ARMA模型的工业电容退化状态研究方法.计算机系统应用,2017,26(7):30–35. http://www.c-s-a.org.cn/1003-3254/5912.html 沈阳市2014年科技计划项目(F14-056-7-00); “高档数控机床与基础制造装备”科技重大专项(2013ZX04007031) 2016-10-26; 收到修改稿时间: 2017-02-17
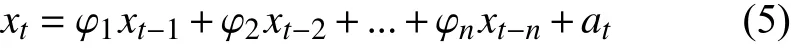
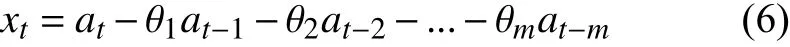
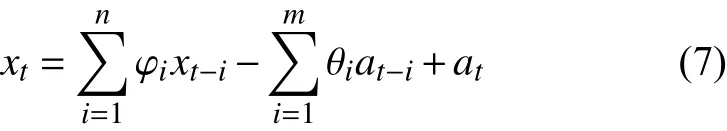
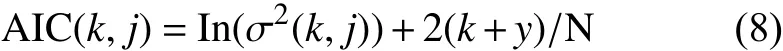
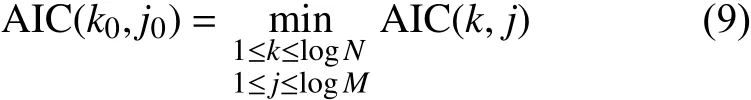

2 实验与结果分析
3 实验结果分析与结论
2(Shenyang Institute of Computing Technology Co. Ltd., CAS, Shenyang 110168, China)
