电磁轨道炮电枢馈电位置研究

吴金国， 李海元， 程年凯， 李龙， 栗保明

(1.南京理工大学 瞬态物理国家重点实验室， 江苏 南京 210094； 2.中国兵器科学研究院， 北京 100089)

电磁轨道炮电枢馈电位置研究

吴金国1， 李海元1， 程年凯2， 李龙1， 栗保明1

(1.南京理工大学 瞬态物理国家重点实验室， 江苏 南京 210094； 2.中国兵器科学研究院， 北京 100089)

轨道炮电枢依靠馈入的脉冲大电流来产生电磁力以驱动弹丸运动。选择合适的电枢馈电位置，有利于减小电枢的启动延迟，也能够减少身管长度的冗余设计。研究了电枢馈电位置的选择对电枢启动时电磁推力的影响，理论推导分析并结合有限元/边界元数值模拟的结果表明：改变电枢的馈电位置，随着接入电路的轨道长度的增加，电枢所受电磁推力逐渐趋于饱和；对于方膛口径轨道炮，在4倍口径位置处馈电可使电枢获得99%的推力，而当轨道间距增加后，则需要在距炮尾更远处馈电方可获得绝大部分推力。分析了炮尾汇流装置对电枢馈电位置的影响，得到纵向汇流方式比横向汇流方式更有利于缩短电枢距炮尾的馈电距离。

兵器科学与技术; 电磁轨道炮; 4倍口径法则; 电感梯度; 有限元； 边界元; 装填

0 引言

电磁轨道炮利用高幅值脉冲电流产生的巨大洛伦兹力推动发射组件达到超高速，是一种很有发展前景的新概念兵器[1]。轨道炮可视为一个直线电机，沿轨道滑行的电枢则是滑动电刷。电枢与轨道组成的电流回路形成了电感，轨道电感梯度是一个重要的物理参数，电枢所受电磁推力Fp与电感梯度L′及电流值I有如下关系[2]：Fp=0.5L′I2. 因此，电枢在启动时受到的电磁推力，除与该时刻的电流值相关外，还取决于其馈电位置的轨道电感梯度值。电枢的馈电位置也即电枢的装填位置，因此电枢的装填位置决定了其启动时的受力情况。电枢启动时较大的电磁推力一方面可以减少电枢的启动延迟，获得较快的响应，降低电枢和轨道初始阶段的烧蚀；另一方面，研究和优化电枢的装填位置，也能够避免发射器长度的冗余设计，因为过多的装填长度必将会消耗发射器的有效加速长度。此外，一些其他应用领域，如空间发射、电磁弹射等，用于电枢加速的轨道一般较长，多采用分段式多步馈电[3-4]的方式以提高发射效率。分段式多步馈电型发射器的设计，需明确每个馈电段在距电枢多远的位置接通电流才能确保其获得最大的推力，从而优化整个发射器结构。目前，大部分学者[5-10]给出的电感梯度计算公式均未考虑电枢轴向位置的影响，马歇尔等[11]通过数值计算方法研究了方膛口径轨道炮装填位置对电枢推力的影响，得出了著名的 “4倍口径法则”。该法则指出了电枢在距轨道后膛多远的位置插入，可以确保接通电流时获得最大的推力。由于“4倍口径法则”是基于方膛口径轨道炮计算得出的，为了对矩形轨道炮的装填及分布式馈电型轨道炮的设计有一个通用的参考，本文通过理论公式推导并结合数值模拟研究了矩形口径轨道炮电枢馈电位置对其启动时推力的影响规律。

1 电枢馈电位置对电磁推力影响的理论分析

当电流一定时，电枢启动时的推力取决于装填位置的电感梯度值。电枢的装填位置直接决定了放电初始时刻的轨道通流长度，研究电枢馈电位置对启动时电磁推力的影响，实际上就变为研究轨道通流长度对电感梯度的影响。

图1是矩形口径电磁轨道发射器示意图，s是轨道间距，h是轨道高度，w是轨道厚度，ha是电枢高度，xP表示电枢的馈电位置。电磁轨道炮内弹道过程通常只有2～10 ms，在如此短时间内，电磁场来不及扩散到轨道深处，电流趋于轨道表面，并且由于邻近效应[12]，主要趋于轨道的内侧表面。在电枢启动阶段，电流趋肤效应尤为明显。为了分析电枢在不同馈电位置时所受的电磁推力，这里假设电流全部集中于轨道内侧表面，并均匀分布。这样，轨道内表面上的电流就可以简化为一个个均匀分布的电流线元。根据毕奥- 萨伐尔定律，长度为l的电流线元，在空间P点(xP,yP,zP)产生的磁场强度为

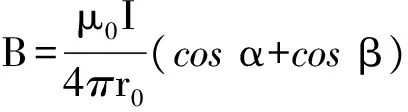
(1)

式中：μ0为真空磁导率；r0为空间P点距电流线元的垂直距离；α、β分别是P点和线元两端点的连线与线元之间的夹角。

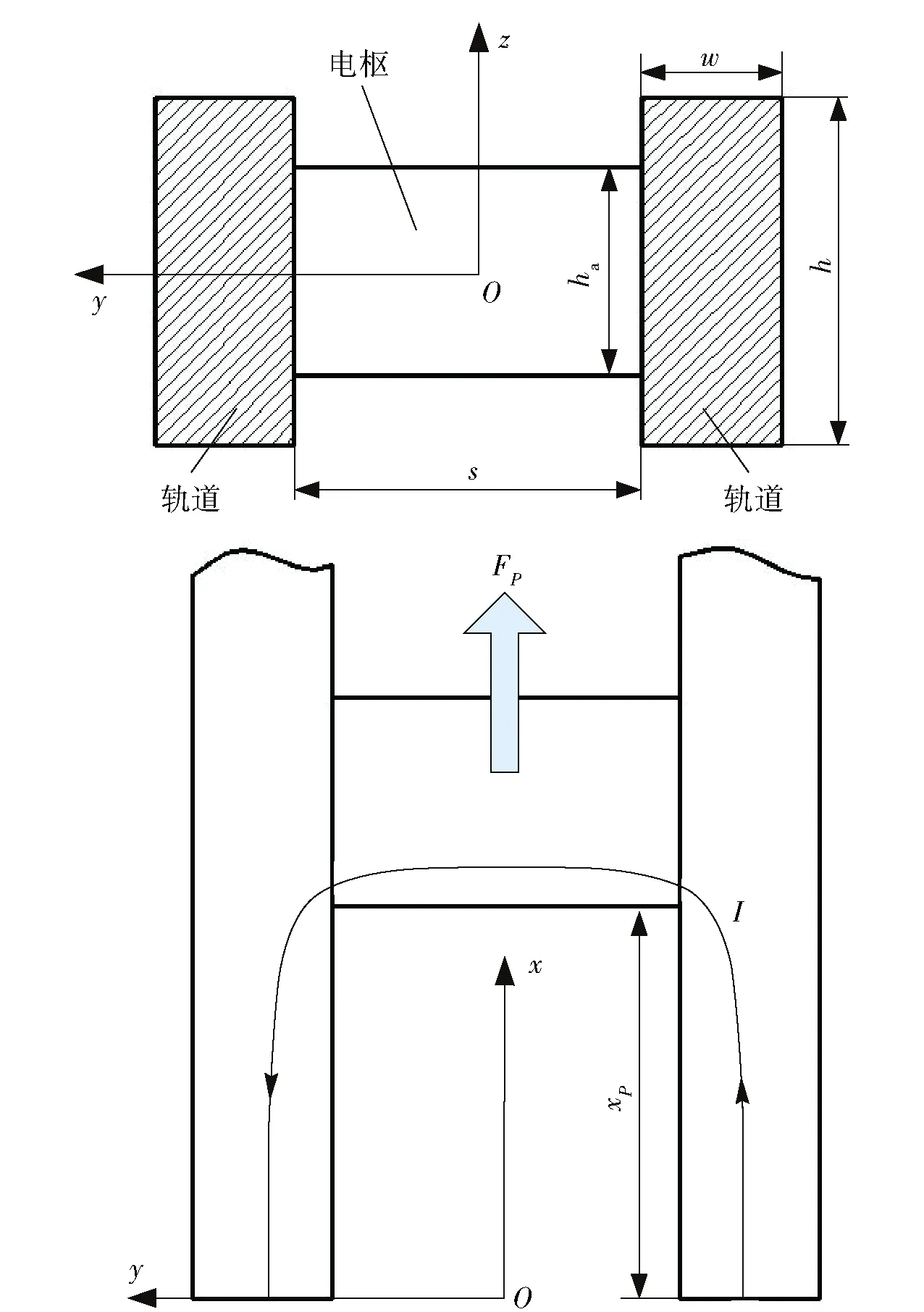
图1 矩形口径电磁轨道发射器示意图Fig.1 Schematic diagram of a rectangle caliber electromagnetic launcher

将轨道上每个电流元在P点产生的磁场进行积分，就得到轨道面电流在P点产生的磁场，而对电枢推力起作用的是z向磁场分量。图1中两根轨道在P点沿z方向产生的磁场分量分别为

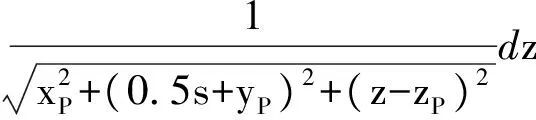
(2)

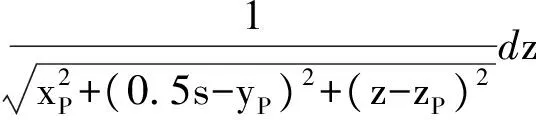
(3)

此处，P点的xP坐标反映了电枢的装填位置，(2)式、(3)式积分后得到：

(4)

(5)

P点沿z方向的磁场分量为二者之和

B=Ba+Bb.

(6)

在电流趋肤效应下，电枢上的电流主要趋于电枢的尾部薄层内。在xP位置处的Oyz平面上，z向磁场强度分布如图2所示，为一个马鞍面的形状。

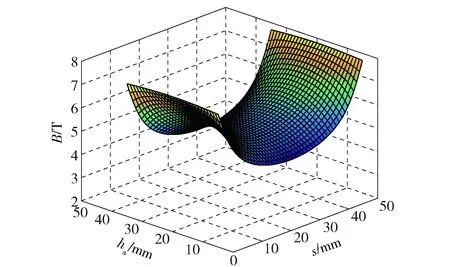
图2 电枢xP位置处Oyz平面上z向磁场强度分布Fig.2 Distribution of magnetic field in direction z on plane Oyz of armature at position xP

为了计算电枢所受的电磁推力，推导时做如下简化：将电枢面上的磁场强度近似用电枢中心的磁场代替，即yP=0,zP=0,得到：

(7)

电枢所受电磁推力为

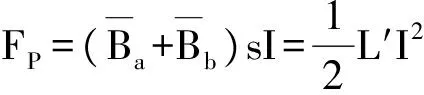
(8)

得到电感梯度L′随电枢装填位置xP的变化关系为

(9)

显然，f(xP)是单调增函数，且有

(10)

即电感梯度不会随着xP的增加而无限增大，而是趋于一个最大值。设η为电感梯度最大值的百分比，0<η<1，令：

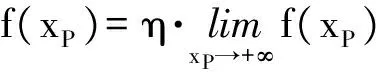
(11)

可求得对应η时的xP值为

(12)

根据(12)式可以计算出想要在启动时获得最大推力百分数η所需要的装填位置xP.

轨道高度h是反映发射器口径的参数，为作无量纲化处理，将xP、s表示为h的倍数。(12)式变换得到：

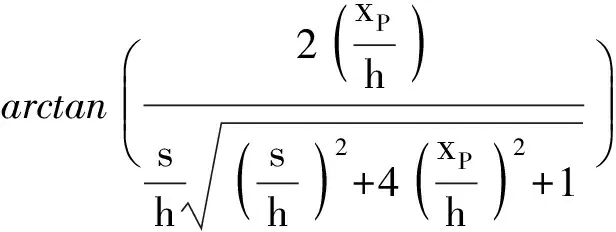
(13)

式中：xP/h为电枢装填位置与口径的比值。根据(13)式可计算出对应xP/h时的最大推力百分数η.

2 结果与讨论

2.1 影响规律分析

(12)式表明，当轨道炮炮膛截面形状(s/h)确定后，即可根据想要获得的最大推力百分比η来选择电枢的装填馈电位置。(13)式表明，η值不仅仅与xP/h有关，还取决于轨道间距s与轨道高度h的比值，在同样的xP/h位置处，η随着s/h的增大而减小。表1是当xP/h取值0.5～8.0，s/h取值0.5～5.0时，η的变化结果，图3是此变化的直观显示。当s/h≤1.0时，在4倍口径位置处，可以获得超过99%的推力，这与马歇尔等[11]的结论是一致的。而当s/h≥2.0，要想在电枢启动时获得超过99%的推力，则需要在更大口径倍数的位置处装填。尽管s/h对η值的分布规律有影响，但这种影响在s≫h的情况下才体现得较为明显。当s/h值接近1，即发射器近似为方膛口径的情况下，可以简单认为，在4倍口径处装填即可获得绝大部分的推力。

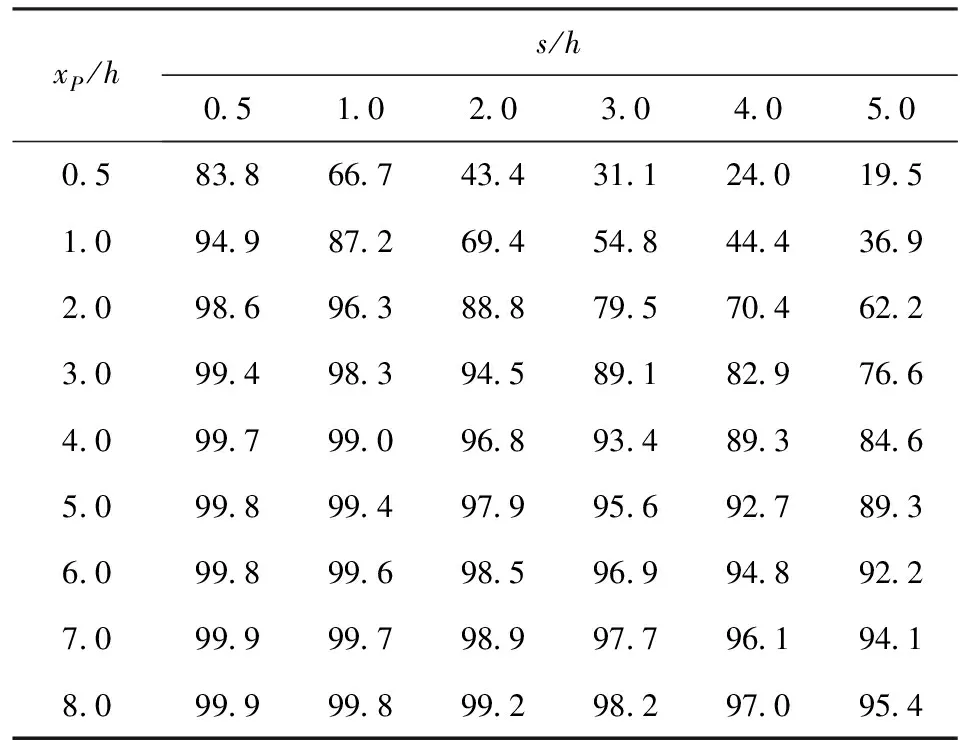
表1 η随着xP/h及s/h的变化Tab.1 Change of η with xP/h and s/h %

图3 η随着xP/h及s/h的变化Fig.3 Change of η with xP/h and s/h

2.2 三维瞬态涡流场模拟及分析

为了进行验证，下面建立轨道炮的三维瞬态涡流场计算模型进行分析。为了减小计算规模，模型中只考虑电枢和轨道，忽略支撑绝缘部件及封装外壳对电磁场的影响。数学模型基于麦克斯韦方程组，忽略位移电流产生的磁场，以标量电位和矢量磁位为未知量，并引入库伦规范，将麦克斯韦方程组变换得到瞬态涡流场控制方程[13-14]为

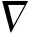
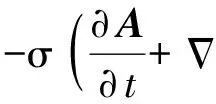
(14)

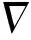
(15)

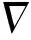
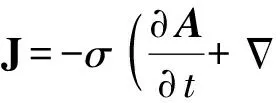
(16)

(17)

电枢受到的电磁力为

F=∫ΩJ×BdV.

(18)

对于开放式边界问题，基于时域有限元/边界元耦合方法建立三维电磁场计算模型，导体区域采用有限元法求解，非导体区域采用边界元法求解，可以减小计算规模。

对于瞬态涡流场问题，还需加上正确的边界条件[15-16]和相应的初始条件。本文中，初始时刻以轨道端面施加的电流为已知量。

采用八节点六面体单元对计算模型进行离散，其中C形电枢划分为5 400个单元，轨道划分为8 600个单元，网格划分如图4所示。将电枢分别装填于不同的位置进行馈电，对其启动时的电动力场进行了计算模拟。选用了表2所示两组参数进行比较分析，B组与A组的区别是增加了轨道间距s.

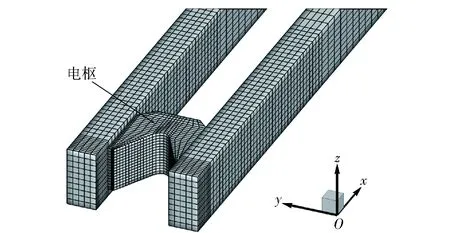
图4 电枢轨道三维网格划分Fig.4 3D finite element model of armature and rails

A组，轨道尾端面施加的激励电流I=800 kA，图5是装填位置xP=20 mm，某一时刻电枢与轨道上的电流密度、磁感应强度及电磁力分布。由于瞬态趋肤效应及邻近效应的作用，轨道上电流主要集中分布在内侧表面附近，距内侧表面4 mm厚度的区域内所流过的电流占轨道截面总电流的约85%。电枢上的磁感应强度、电磁力在喉部区域最大。改变电枢的馈电位置，随着距炮尾馈电距离xP的增加，电枢上的磁感应强度逐渐增大，并趋于饱和。图6是电枢上选取的图5(b)中A、B、C3个点处磁感应强度的变化，在150 mm处已基本趋于饱和，电枢上的电磁推力也达到一个稳定的最大值，约170 kN(见图7(a))。最大推力百分比η在4倍口径处达到99%以上(见图7(b))。

表2 两组计算参数Tab.2 Two groups of calculation parameters

图5 有限元/边界元模拟出的多场分布(A组：xP=20 mm)Fig.5 Distribution of muti-fields simulated by FEM/BEM (Group A: xP=20 mm)

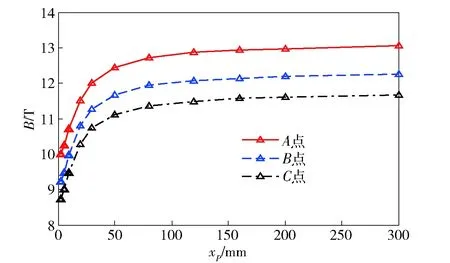
图6 电枢上3个点磁感应强度随馈电位置的变化(A组)Fig.6 Magnetic flux densities of three points on armature versus feeding position (Group A)

需要说明的是，图7中理论分析的曲线与有限元计算得到的离散点在xP→0时偏差较大。产生偏差的原因为，理论推导时假设电流全部从电枢尾面上流过，不考虑电流沿电枢厚度方向的扩散；而在有限元计算中，电枢厚度在建模时得以体现，电流沿厚度方向存在扩散，所以当xP→0 时，有限元计算出的推力FP≠0.

B组，轨道间距s增加到120 mm，为轨道高度h的3倍。电枢的推力依然是随着电枢馈电距离的增加逐渐增大，趋于饱和值约260 kN(见图8(a))。与A组不同的是，最大推力百分比η在8倍口径后达到99%以上(见图8(b))。这说明要想使电枢达到预定的最大推力百分比η时所需的馈电距离口径倍数(xP/h)是与s/h相关的，三维瞬态涡流场数值模拟的结果与前面理论分析得到结论基本吻合。

图8 B组结果Fig.8 Results of Group B

2.3 汇流方式对电枢馈电位置的影响

轨道炮一般需要兆安级的电流，炮尾的汇流装置通常不可避免。为此，讨论了两种炮尾汇流排接入方式对电枢馈电位置的影响，分别是横向及纵向汇流，如图9所示。

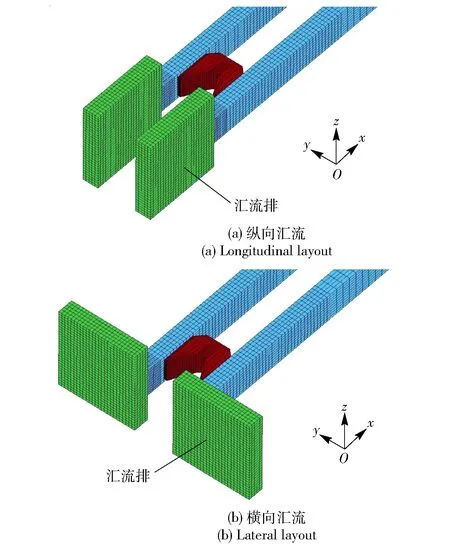
图9 两种汇流方式Fig.9 Two types of buss-bar layout

电枢在距炮尾相同的位置处(30 mm)进行馈电，纵向汇流时电枢获得的电磁推力为161 kN，横向汇流时推力为98 kN，而不考虑炮尾汇流装置影响时推力为148 kN. 由此可见，采用纵向汇流方式，相当于延长了接入电路的轨道长度，从而使得电枢推力饱和的馈电位置也相应后移。而采用横向汇流方式，汇流排上电流形成的磁场与轨道上电流形成的磁场方向相反，削弱了电枢上z方向上的磁场强度，从而使电枢受到的电磁推力相应减小。为使电枢电磁推力达到饱和，就需要进一步增加距炮尾的馈电距离。因此，纵向汇流方式与横向汇流方式相比，采用更短的馈电距离即可使电枢推力达到饱和。这对于炮尾馈电型及分布式馈电型轨道炮馈电装置的设计均有重要的参考意义。

3 结论

本文研究了轨道炮电枢馈电位置的优化问题，通过理论推导并结合有限元/边界元数值模拟，对矩形口径轨道炮电枢电磁力饱和时馈电位置的选择进行了定量化的分析，得到以下主要结论:

1) 对电枢所受电磁推力起作用的只是电枢后面一段有限长度的轨道。改变电枢的馈电位置，随着接入电路的轨道长度增加，轨道电流在电枢上产生的磁场趋近饱和，相应的电枢受到的电磁推力也逐渐趋近饱和。

2) 对于方口径轨道炮，电枢在4倍口径位置处馈电即可获得99%的推力，即通常所说的“4倍口径法则”。然而，当轨道间距增加后，则需要在距炮尾更远的位置处馈电方可使电枢上的电磁推力达到饱和。

3) 当考虑炮尾接入的汇流排时，使电枢推力达到饱和的馈电位置也会受到影响。采用纵向汇流方式可以缩减电枢距炮尾的馈电距离，而横向汇流方式则加长了馈电距离，此时，“4倍口径法则”需要根据实际情况作相应调整。

References)

[1] Fair H D. Advances in electromagnetic launch science and technology and its applications[J]. IEEE Transactions on Magnetics, 2014,45(1): 225-230.

[2] 王莹, 肖峰. 电炮原理[M]. 北京: 国防工业出版社, 1995. WANG Ying, XIAO Feng. The principle of electrical gun[M]. Beijing: National Defense Industry Press, 1995.(in Chinese)

[3] Hundertmark S, Schneider M, Vincent G. Payload acceleration using a 10-MJ DES railgun[J]. IEEE Transactions on Plasma Science, 2013, 5(1):1455-1459.

[4] Zhou Y, Yan P, Sun Y, et al. Design of a distributed-energy-store railgun[J]. IEEE Transactions on Plasma Science, 2011, 39(1): 230-234.

[5] Kerrisk J F. Current distribution and inductance calculations for railgun conductor[R]. NM,US: Los Alamos National Laboratory, 1981.

[6] Grover F W. Inductance calculations：working formulas and tables[M]. New York: Dover Publication, 1962.

[7] Batteh J H, Powel J D. Analysis of plasma arcs in arc-driven rail guns[J]. IEEE Transactions on Magnetics, 1984,20(2):336-339.

[8] 聂建新, 韩晶晶, 焦清介, 等. 电磁轨道发射器的几何尺寸对电感梯度的影响[J]. 高电压技术, 2010,36(3): 728-732. NIE Jian-xin, HAN Jing-jing, JIAO Qing-jie, et al. Effect of rail-type electromagnetic launcher dimensions on inductance[J]. High Voltage Engineering, 2010,36(3): 728-732.(in Chinese)

[9] 孙立强, 袁伟群, 严萍. 基于时频分析的电磁轨道发射电感梯度研究[J]. 电工电能新技术, 2008,27(2):38-42. SUN Li-qiang, YUAN Wei-qun, YAN Ping. Study of rail inductance gradient during EM rail launch based on time-frequency analysis[J]. Advanced Technology of Electrical Engineering and Energy, 2008,27(2):38-42.(in Chinese)

[10] 张惠. 电磁轨道炮电感梯度的研究和解析计算[D]. 秦皇岛：燕山大学, 2013. ZHANG Hui. Research and analytical calculation of the railgun inductance gradient[D] Qinhuangdao: Yanshan University, 2013.(in Chinese)

[11] 马歇尔 R A，王莹. 电磁轨道炮的科学与技术[M]. 曹延杰， 译. 北京：兵器工业出版社, 2004. Marshall R A, WANG Ying. Science and technology of ailguns [M]. CAO Yan-jie, translated. Beijing: Publishing House of Ordnance Industry, 2004.(in Chinese)

[12] Lou Y T, Li H Y, Li B M. Research on proximity effect of electromagnetic railgun[J]. Defense Technology, 2016,12(3): 223-226.

[13] 杨宪章, 邹玲, 樊亚东，等. 工程电磁场[M]. 北京: 中国电力出版社, 2011. YANG Xian-zhang, ZOU Ling, FAN Ya-dong, et al. Engineering electromagnetic field[M]. Beijing: China Electric Power Press, 2011.(in Chinese)

[14] 谢德馨. 三维涡流场的有限元分析[M]. 北京: 机械工业出版社, 2008. XIE De-xin. Finite element analysis of 3D eddy current field[M]. Beijing: China Machine Press, 2008.(in Chinese)

[15] 林庆华, 栗保明. 电磁轨道炮三维瞬态涡流场的有限元建模与仿真[J]. 兵工学报, 2009, 30(9):1159-1163. LIN Qing-hua, LI Bao-ming. Finite element analysis of 3D transient eddy field in electromagnetic railgun[J]. Acta Armamentarii, 2009, 30(9): 1159-1163.(in Chinese)

[16] 林庆华, 栗保明. 电磁轨道炮瞬态磁场测量与数值模拟[J]. 兵工学报, 2016, 37(10): 1788-1794. LIN Qing-hua, LI Bao-ming. Measurement and numerical simulation of transient electromagnetic field in railgun [J]. Acta Armamentarii, 2016, 37(10): 1788-1794.(in Chinese)

Research on Feeding Position of Armature in Railgun

WU Jin-guo1, LI Hai-yuan1, CHENG Nian-kai2, LI Long1, LI Bao-ming1

(1.National Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China;2.Ordance Science and Research Academy of China, Beijing 100089, China)

The armature of railgun relies on the electromagnetic thrust generated by pulse current to drive a projectile. The appropriate feeding position of armature helps to reduce the startup delay of armature, and reduce the redundant length of rails. The influence of feeding position of armature on electromagnetic thrust at startup position is studied. Theoretical analysis and numerical simulations of hybrid finite element and boundary element method show that the electromagnetic thrust on the armature gradually approaches a saturation, with the increase in length of the rails in circuit by changing the feeding position of armature. For a square caliber railgun, the armature acquires 99% electromagnetic thrust at the four caliber position. However, with the increase in the distance between rails, the feeding position should be far more from the breech for the armature to get the most thrust. The influence of breech buss-bar on the feeding position of armature is also analyzed. Compared with the lateral layout, the longitudinal layout is more conducive to shorten the feeding length of armature.

ordnance science and technology; electromagnetic railgun; four caliber rule; inductance gradient; finite element method； boundary element method; load

2017-01-10

吴金国(1989— )，男，博士研究生。E-mail: wujg8848@163.com

李海元(1972— )，男，副研究员，硕士生导师。E-mail: li_haiyuan@163.com

TM153+.1； TJ866

A

1000-1093(2017)06-1052-07

10.3969/j.issn.1000-1093.2017.06.002