面向任务的作战单元携行备件配置优化方法研究
2017-07-10阮旻智傅健周亮王俊龙
阮旻智, 傅健, 周亮, 王俊龙
(1.海军工程大学 科研部, 湖北 武汉 430033; 2.海军工程大学 兵器工程系, 湖北 武汉 430033)
面向任务的作战单元携行备件配置优化方法研究
阮旻智1, 傅健1, 周亮2, 王俊龙1
(1.海军工程大学 科研部, 湖北 武汉 430033; 2.海军工程大学 兵器工程系, 湖北 武汉 430033)
备件是作战单元的重要保障物资,能够使故障设备迅速恢复战斗力并投入作战使用。提出一种基于等效寿命转换的冗余系统备件需求计算方法,根据可修备件控制理论,以任务成功概率为目标函数,建立了基于多阶段任务的携行备件动态配置模型,通过引入拉格朗日约束因子,提出了多约束条件下的备件方案优化方法。通过算例,对结果进行了分析,计算得到的携行备件方案能够满足所有约束条件,并且与ExtendSim仿真结果之间的偏差小于3%,验证了该模型的正确性,为面向任务的携行备件优化提供了一种解决思路。
兵器科学与技术; 面向任务; 作战单元; 携行备件; 动态优化; 冗余系统
0 引言
作战单元是部队执行作战任务、实现战术目标的军事实体(如舰艇编队、坦克团、飞行大队等),一般由基本作战单元和保障单元组成,其中,基本作战单元是具有独立作战能力的最小单元(如单舰平台),保障单元是对装备进行故障修理和维修资源供应的保障机构。对于组成结构复杂、集成度较高的装备,如飞行器、舰船动力装置、雷达阵面等,一般采用冗余结构设计模式,用以满足系统任务可靠性指标。系统冗余会增加设备的安装空间,而且由于任务期间备件携行能力有限,若故障设备的备件发生短缺,会导致装备停机,从而影响作战单元的任务成功率。对此,需要合理规划备件的携行方案,以提高作战单元装备可用度。
备件是作战单元的重要保障物质,一直以来,备件规划是装备维修保障工程领域中的重点和难点问题。在备件保障优化建模方面:Sherbrooke提出了可修备件多级库存控制(METRIC)模型[1],该理论被广泛运用于各领域的工程实践,如空军航空装备[2]、海军舰船装备[3]、民机航材[4]、面向多等级多层级保障系统备件优化[5-6]等,并在METRIC理论基础上进行了拓展,目前,几种常见的备件配置模型体系有多层级备件模型体系[7]、多等级多层级备件优化模型体系[8]、备件动态配置优化模型体系[9]等。在冗余系统建模方面:文献[10]在考虑了备件报废的情况下,建立了冷备份冗余系统两等级单层级可修复备件优化模型;文献[11]提出任意寿命分布单元表决系统的备件需求量解析算法;文献[12]对面向对象建模的Petri网进行了扩展,建立了多任务阶段(MSP)失效模型;文献[13]研究了冷冗余系统初始备件配置方法。在基于任务的携行备件保障优化研究方面:文献[14]研究了备件质量、体积、费用等多约束条件下,建立了舰船装备携行备件配置优化模型,通过引入拉格朗日因子,采用一种动态更新策略对模型进行求解;文献[15]以远海训练任务的舰船编队为背景,采用蒙特卡洛仿真和并行粒子群算法,对携行备件优化方法进行研究。
上述列举的文献并没有考虑冗余系统任务剖面对携行备件方案及系统任务成功概率的影响,而且对备件方案评估及其优化结果的合理性方面缺乏有效的验证依据。本文在上述研究基础上,考虑阶段性任务剖面的影响,建立作战单元冗余系统携行备件动态配置模型,并对模型算法的有效性进行验证。
1 基于等效寿命的冗余系统备件需求率
不考虑人员、工装具、技术资料等维修资源约束下,保障单元对装备故障件具有一定的修复能力,修复后的故障件可作为新的备件进行轮换使用。按照装备层次结构,可将备件分为现场更换单元(LRU)和车间更换单元(SRU)。
令i=1,2,…,I,表示基本作战单元编号;i=0表示保障单元;j=1,2,…,J,表示备件项目编号;T表示任务周期;t(t∈T)表示任务阶段(t=1,2,…)。对于冗余结构部件,可采用一种等效寿命件的方法将其视为单部件来处理。


图1 冗余系统等效寿命后的物理结构Fig.1 Physical structure of redundant system after equivalent life tansformation


(1)
式中:Kij(t)表示在t时刻,确保基本作战单元i正常工作所需LRUj完好数量,Kij(t)会随任务阶段t而变化;Nij为LRUj的冗余数量;MTBFj为单个LRUj的平均故障间隔时间。

令Inden(j)表示部件j在系统中的层级数,对于第1层级部件LRUj,即Inden(j)=1,基本作战单元i在t时刻的需求率为

(2)
式中:DCj表示占空比;HWm(t)为系统在任务阶段t时刻的累积工作强度。当Inden(j)>1时,表示LRU子部件SRU,则基本作战单元在t时刻对部件j的需求率为
λij(t)=λi,Aub(j)(t)(1-NRi,Aub(j))qij,
(3)
式中:Aub(j)表示j的母体;NRi,Aub(j)为作战单元i不能对故障件j的母体进行修复的概率;qij为部件j的故障隔离概率。
对于保障单元i(i=0),其备件需求率包括两项:一是其所保障的作战单元不能完成故障件修理的数量之和,该部分需要送到保障单元进行修理;二是保障单元对故障件j的母体Aub(j)进行修理时而产生对备件j的需求,则
λi,Aub(j)(t)(1-NRij)qij.
(4)

(5)
式中:Kij(t)表示t时刻,确保基本作战单元i装备正常工作所需LRUj完好数量;Nij为LRUj的冗余数量;MTTRj、Cj、Vj分别表示冗余系统中LRUj单部件的平均维修时间、单价和体积。由于LRU属现场更换单元,因此不考虑其所属的SRU冗余,等效后SRU的计算方法与LRU类似。上述建立的备件需求率模型中,主要考虑任务期间系统故障所产生的备件需求,战损条件下的备件需求,具有明显的突发性和随机性特征,并且影响因素众多,建模过程复杂,因此,本文暂不考虑战损的影响。
2 基于任务的携行备件动态配置模型
2.1 备件维修供应模型
设PKj(r,t)为故障件j在r时刻开始进行修理,在t时刻仍未修好的概率,MTTRj表示基本作战单元i、故障件j的平均维修时间。根据动态帕尔姆定理[1],PKj(r,t)服从均值为1/MTTRj的指数分布:

(6)
t时刻,故障件j在修数量服从均值为E[XRij(t)]的泊松分布(引用文献[1]中的结论),即
PKj(r,t)]dr.
(7)
令OTij为备件补给运输时间,则在t时刻,正在补给的备件数量服从均值为E[XSij(t)]的泊松分布(引用文献[1]中METRIC模型的结论),即

(8)
对故障件j进行修理时,会因等待其子部件k(k∈Sub(j))维修会造成故障件j修理延误,该部分可用故障件j所属子部件k短缺数之和来近似。则在t时刻,故障件j修理延误数量期望值E[DRij(t)]为
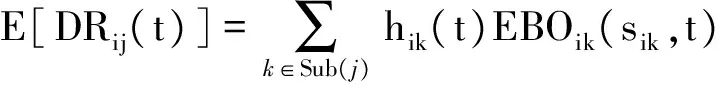
(9)
式中:k∈Sub(j)表示j的子部件集合;EBOik(sik,t)表示t时刻,备件配置量为sik时的期望短缺数;hik(t)为备件维修延误短缺数分配比例因子,其计算方法为
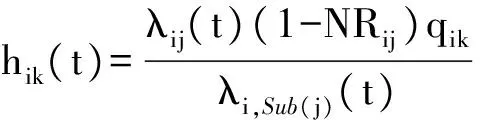
(10)
式中:λi,Sub(j)(t)表示t时刻,j的子部件k需求率;qik为子部件k的故障隔离概率。当子部件k发生短缺时,其短缺总数会以比例因子hik造成故障件j修理延误,该短缺总数分布概率服从二项分布[17]。因此,故障件j修理延误数量方差为
hik(t)(1-hik(t))EBOik(sik,t)],
(11)
式中:VBOik(sik,t)表示t时刻,备件配置量为sik时的短缺数方差。
不考虑外部补给,则对保障单元补给的备件数量为0. 对于基本作战单元i,在t时刻,备件j补给延误数量期望值E[DSij(t)]为
E[DSij(t)]=fij(t)EBO0j(s0j,t),
(12)
式中:EBO0j(s0j,t)表示t时刻,备件配置量为s0j时的期望短缺数;同理,fij(t)为备件补给延误短缺数分配比例因子,其计算方法为
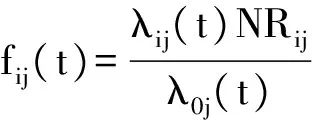
(13)
式中:λ0j(t)表示t时刻,保障单元对备件j的需求率。当保障单元发生备件短缺时,对基本作战单元i以比例因子fij(t)造成备件补给延误,该短缺数概率服从二项分布[17]。因此,备件补给延误数量方差V[DSij(t)]为
fij(t)(1-fij(t))EBO0j(s0j,t),
(14)
式中:VBO0j(s0j,t)表示t时刻,备件配置量为s0j时的短缺数方差。
备件维修供应周转量主要由在修备件数量、备件补给数量、修理延误数量以及备件补给延误数量4部分构成,则t时刻,备件维修供应周转量均值E[Xij(t)]、方差V[Xij(t)]分别为
E[Xij(t)]=E[XRij(t)]+E[XSij(t)]+
E[DRij(t)]+E[DSij(t)],
(15)
V[Xij(t)]=E[XRij(t)]+E[XSij(t)]+
V[DRij(t)]+V[DSij(t)].
(16)
2.2 备件期望短缺数
备件短缺数记为B(X|s),其中X表示备件维修供应周转量,亦称待收备件数,s表示备件量,则B(X|s)[18]定义为

(17)
令t时刻,基本作战单元i、备件j的期望短缺数为EBOij(sij,t),短缺数方差为VBOij(sij,t),则
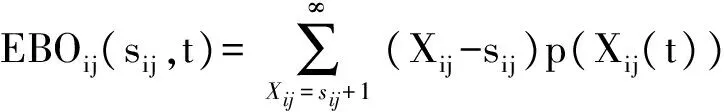
(18)
VBOij(sij,t)=E[BOij]2-[EBOij]2,
(19)

(20)
式中:p(Xij)表示备件维修供应周转量概率分布函数。当E[Xij(t)]=V[Xij(t)]时,p(Xij)服从泊松概率分布;当E[Xij(t)]
2.3 备件配置优化目标函数
令基本作战单元i中第z个装备在t时刻完成任务的概率为ρiz(t),可用度为Aiz(t),定义
(21)
式中:Mission(t,z)表示t时刻,系统完成任务所需要的设备集合。令基本作战单元i在t时刻完成任务的概率为ρi(t),则t时刻整个作战单元的任务成功概率ρs(t)为
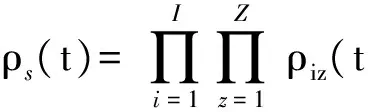
(22)
通过等效寿命转换的方法,可将系统中的冗余结构等效为串联结构,因此,作战单元i、装备z在t时刻可用概率为

(23)
式中:j∈(Inden(j)=1)表示装备z中第1层级部件LRU集合。
考虑到任务系统携行能力和备件存储空间的限制,将装备可用度、备件质量和体积作为约束条件。因此,携行备件配置优化目标函数如下:

(24)
s.t.min(ρs(t))≥ρ0,
(25)

(26)
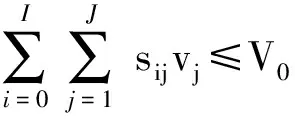
(27)
式中:sij为备件的任务携行量;i=0表示保障单元;i≠0表示基本作战单元;cj为备件费用;ρ0为规定的任务成功概率指标;mj表示备件j的质量,M0表示质量约束指标;vj表示备件j的体积;V0为体积约束指标。
3 模型求解及算法设计
3.1 模型求解算法
设λc为费用约束因子,γm为质量约束因子,ηv为体积约束因子,并且令λc=1.rj为备件j的规模总成,表示备件费用、体积、质量等因素的加权之和,则定义
rj=λccj+γmmj+ηvvj.
(28)
令当前备件配置方案下,备件资源规模总成组合为ri=(ri1,ri2,…,rij,…riJ),该方案下,基本作战单元i、备件j数量加1后,备件资源规模总成组合变为r′i=(ri1,ri2…,r′ij,…,riJ),对(22)式等号两段取对数,可得到r′与r关于可用概率ρs(t)的1阶差分方程为
Δρs(rij,t)=lnρs(r′i,t)-lnρs(ri,t)=
lnρs(r′ij,t)-lnρs(rij,t).
(29)
每增加一项备件后,将备件方案保障效能(任务成功概率)增量与备件资源规模总成增量之比定义为边际效应值δij:
(30)
模型算法优化迭代过程中,通过比较每项备件的边际效应值δij,将最大值max (δij)所对应的备件配置数量加1,依此递推循环,直到满足规定的指标约束后,算法结束。
3.2 拉格朗日约束因子的确定
记初始质量因子为γm0,初始体积因子为ηv0,其确定方法如下:
1)令γm=ηv=0,即备件资源规模总成中只考虑费用约束,通过边际算法求解得到一组费用约束下的最优备件方案s0;
2)在s0基础上,计算该方案下的备件费用C(s0)、质量M(s0)和体积V(s0);
3)确定γm0和ηv0的初始值,其方法如下:
γm0=C(s0)/M(s0),
(31)
ηv0=C(s0)/V(s0).
(32)
在确定的γm0和ηv0下,计算得到另一组备件方案,记为s. 若该方案所对应的备件质量或体积超过其设定的指标时,需要增加γm0或ηv0,以形成惩罚因子,其增量的确定方法为
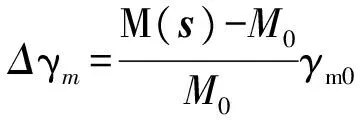
(33)
(34)
通过(33)式和(34)式对拉格朗日约束因子进行动态更新和调整。
在既定的指标下,可能会出现一种特殊情况,即无论如何调整因子γm及ηv的数值,都不能得到一组满足所有约束条件的解,在此情况下,需要重新设定约束条件,可适当降低(25)式中的任务成功概率指标ρ0,或增加指标M0和V0.
4 算例分析
4.1 任务想定
以地对空作战训练任务为例,作战单元由3个地对空作战平台(基本作战单元)和1个维修保障分队(保障单元)组成,基本作战单元由警戒雷达系统、防空武器系统及电子战防御系统构成。
设任务周期为30 d,规定任务成功概率不小于0.95,携行备件体积不超过26.5 m3,质量不超过530 kg. 根据任务过程中各系统之间的工况要求,可将任务周期分解为4个任务阶段,包括:
1)战前准备阶段:接受上级命令,并到达指定的作战区域,由于该阶段会随时受到空中目标威胁,因此,警戒雷达系统和电子战防御系统需要保持完好状态;
2)防空作战阶段:定期开展对多批次空中目标进行威胁等级预判、目标定位、运动参数分析,并进行火力射击;
3)电子战防御阶段:对突防的空中威胁辐射源进行电子干扰;
4)撤离阶段:作战任务结束后,返回基地。
令各任务阶段的持续时间分别为8 d、4 d、6 d、12 d. 任务系统工作状态要求及冗余情况见表1.

表1 任务阶段系统工况及冗余要求Tab.1 Operating conditions and redundancy requirements of system in the different mission phases
4.2 解算步骤
根据模型算法的求解步骤,令γm=ηv=0,通过模型求解得到费用约束下的最优备件方案s0,此时,系统任务成功概率ρ0(s0)=0.956 3,备件费用C(s0)=262.5万元,质量M(s0)=559.5 kg,体积V(s0)=30.18 m3. 利用该数据,将约束因子γm及ηv的进行归一化处理得到初始值分别为
γm0=C(s0)/M(s0)=262.5/559.5=0.47,
(35)
ηv0=C(s0)/V(s0)=262.5/30.18=8.7.
(36)
由于规定的指标M0=530 kg,V0=26.5 m3,因此方案s0中携行备件质量和体积均未满足条件。通过引入γm及ηv,重新计算得到另一组备件方案,记为s,该方案下,系统任务成功概率ρ0(s)=0.950 8,携行备件费用C(s)=271万元,质量M(s)=514 kg,体积V(s)=25.1 m3. 各项指标均满足设定的约束条件,因此,方案s为优化计算得到的最终结果。
通过调整各约束因子的值,能够在不同的约束条件下计算生成最优携行备件方案,见表2.
1)费用约束方案:λc=1,γm=ηv=0;
2)质量约束方案:λc=0,γm=1,ηv=0;
3)体积约束方案:λc=0,γm=0,ηv=1;
4)规模总成约束方案:λc=1,γm=0.47,ηv=8.7.

表2 不同约束条件下的携行备件方案结果Tab.2 Calculated results of carrying spares project under different constraint conditions
4.3 结果分析
根据表2显示的计算结果,可以计算得到各方案所对应的保障效能及指标值(见表3)。在4种备选方案中,只有规模总成方案计算结果满足所有约束条件,因此,该方案为最优方案。
不同约束方案计算结果对比如图2所示。
不同约束下的备件方案最优迭代变化曲线如图3所示,曲线上的所有点都表示当前条件下的最优结果,通过该曲线,便于对备件方案优化计算全过程进行控制,能够辅助决策者对各项指标参数的敏感性进行分析。根据该曲线,能够为备件方案约束指标的设定范围提供依据。
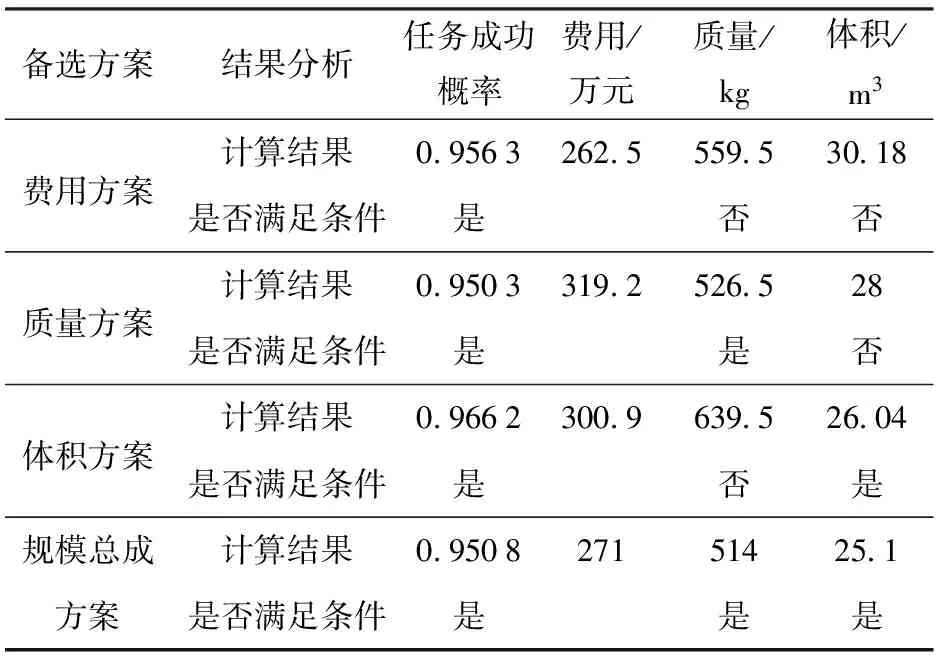
表3 携行备件方案保障效能Tab.3 Support effectiveness of carrying spares project
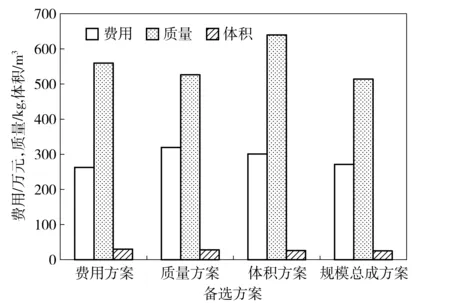
图2 备件方案计算结果对比Fig.2 Comparison of calculated results of spares project

图3 不同约束条件下各方案费效曲线对比Fig.3 Effectiveness vs. cost for different constraint project
4.4 模型数据验证
采用两种方法对本文模型结果的正确性进行验证:一是通过VMETRIC软件工具;二是通过构建的仿真模型体系。其中,VMETRIC是由美国雷神公司开发的一款多等级、多层次、多系统的备件优化工具,曾多次用于美国各军兵种的装备采办、保障性分析、维修保障方案辅助决策等,取得了明显的效果。但VMETRIC是面向稳态条件下的备件优化工具,不能处理多阶段任务下的备件动态优化,对此,本文将装备任务周期分解为多个阶段,将前一个阶段的优化输出结果作为下一个阶段的输入,通过对各阶段备件保障效果分析处理,以此来评价模型计算结果。仿真模型体系是在基于离散事件系统(ExtendSim)的仿真环境下实现的,该系统是由美国ImagineThat公司开发,对于离散事件具有较强的仿真能力。构建的仿真模型体系如图4所示,其中包括备件需求模块、故障修理模块、备件周转运送模块、保障效能指标评估模块、统计模块等。

图4 基于ExtendSim的备件仿真模型Fig.4 ExtendSim-based spares simulation model
采用VMETRIC验证时,将本文模型计算得到的方案结果作为输入条件,计算得到方案评估结果。采用基于ExtendSim的仿真模型体系进行验证时,为了保证计算结果趋于稳定,随机产生200组备件需求数,设定仿真次数为1 000次,仿真时钟按事件发生的逻辑顺序进入相应流程控制。
表4给出了模型验证结果,从中可以看出本文模型计算结果与仿真验证结果之间的偏差均小于3%,模型结果误差在合理的控制范围之内,在一定程度上验证了该模型的正确性。

表4 系统任务成功概率验证结果Tab.4 Validation results of system mission success probability
通过模型验证可知,本文计算结果相比仿真评估结果而言,普遍偏低,并且随着系统任务成功概率的减小,结果偏差会逐渐增大,本文方法得到的结果属于相对保守的方案。造成该现象的主要原因是没有考虑备件需求相关性,即故障停机的设备不会产生备件需求。基于该结论,备件需求率会随着装备任务成功概率变化而发生改变,在算法迭代过程中,需要根据前一次迭代计算结果来调整当前的备件需求输入参数,这样才能保证系统在低可用度情况下的结果准确性。
5 结论
本文以面向任务的作战单元携行备件优化为背景,提出多阶段任务的携行备件动态配置模型。通过案例应用分析可知:在不同的约束条件下,计算得到的携行备件配置方案会存在一定的差别,但最终目标却是一致的,即保证在满足约束条件下,达到规定的任务成功性指标要求。研究结论能够在装备使用阶段,辅助军方对同步配套的装备维修保障资源配置提供决策支持。
References)
[1] Sherbrooke C C. Optimal inventory modeling of systems: multi-echelon techniques[M]. 2nd ed. Boston: Artech House, 2004.
[2] Yoon K B, Sohn S Y. Finding the optimal CSP inventory level for multi-echelon system in air force using random effects regression model[J]. European Journal of Operational Research, 2007, 180(3): 1076-1085.
[3] Sleptchenko A, van der Heijden M C, van Harten A. Effects of finite repair capacity in multi-echelon multi-indenture service part supply systems[J]. International Journal of Production Economics, 2002, 79(3): 209-230.
[4] 解江,刘晓东,段斌,等.多隶属关系下的两级可修复航材储备模型研究[J].系统工程理论与实践,2015,35(3):811-816. XIE Jiang, LIU Xiao-dong, DUAN Bin, et al. Research on the reserve model of two level recoverable spare parts under multi-indenture[J]. System Engineering Theory & Practice, 2015, 35(3): 811-816.(in Chinese)
[5] 阮旻智,李庆民、黄傲林,等.有限维修渠道约束下的多级维修供应系统库存控制[J].航空学报,2012,33(11):2018-2027. RUAN Min-zhi, LI Qing-min, HUANG Ao-lin, et al. Inventory control of multi-echelon maintenance supply system under finite repair channel constraint[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 2018-2027.(in Chinese)
[6] Ruan M Z, Luo Y, Li H. Configuration model of partial repairable spares under batch ordering policy based on inventory state[J]. Chinese Journal of Aeronautics, 2014, 27(3): 558-567.
[7] Ahmad H, Matthieu H. Interval availability analysis of a two-echelon multi-item system[J]. European Journal of Operational Research, 2013, 228(3): 494-503.
[8] Francesco C, Giulio D, Massimo T. Multi-echelon, multi-indenture spare parts inventory control subject to system availability and budget constraints[J]. Reliability Engineering and System Safety, 2013, 119: 95-101.
[9] Elisa A, Matthieu H. On two-echelon inventory systems with Poisson demand and lost sales[J]. European Journal of Operational Research, 2014, 235(1): 334-338.
[10] 薛陶,冯蕴霞,秦强.考虑报废的K/N冷备份冗余系统可修复备件优化[J].华南理工大学学报:自然科学版,2014,42(1):41-45. XUE Tao, FENG Yun-xia, QIN Qiang. Optimization of repairable spare parts for K/N cold-standby redundant system considering scraps[J]. Journal of South China University of Technology:Natural Science Edition, 2014, 42(1): 41-45.(in Chinese)
[11] 刘任洋,李庆民,王慎,等.任意寿命分布单元表决系统备件需求量的解析算法[J].系统工程与电子技术,2016,38(3):714-718. LIU Ren-yang, LI Qing-min, WANG Shen, et al. Analytical algorithm of spare demand for voting system of any life distribution units[J]. System Engineering and Electronics, 2016, 38(3): 714-718.(in Chinese)
[12] Wu X Y, Wu X Y. Extended object-oriented Petri net model for mission reliability simulation of repairable PMS with common cause failures[J]. Reliability Engineering & System Safety, 2015, 136:109-119.
[13] 卢雷,杨江平.k/N(G)结构系统初始备件配置方法[J].航空学报,2014,35(3):773-778. LU Lei, YANG Jiang-ping. Initial spare allocation method fork/N(G) structure system[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 773-778.(in Chinese)
[14] 阮旻智,李庆民,张光宇,等.多约束下舰船装备携行备件保障方案的确定方法[J].兵工学报,2013,34(9):1144-1149. RUAN Min-zhi, LI Qing-min, ZHANG Guang-yu, et al. Optimization method of carrying spare parts support project for warship equipment under multi-constraints[J]. Acta Armamentarii, 2013, 34(9): 1144-1149.(in Chinese)
[15] 张永强,徐宗昌,孙寒冰,等.基于蒙特卡洛仿真和并行粒子群优化算法的携行备件优化[J].兵工学报,2016,37(1):122-130. ZHANG Yong-qiang, XU Zong-chang, SUN Han-bing, et al. Optimization of carried spare parts based on monte carlo simulation and parallel particle swarm optimization algorithm[J]. Acta Armamentarii, 2016, 37(1): 122-130.(in Chinese)
[16] 张志华.可靠性理论及工程应用[M].北京:科学出版社,2012. ZHANG Zhi-hua. Reliability theory and engineering application[M]. Beijing: Science Press, 2012.(in Chinese)
[17] Nowicki D, Randall W S, Ramirez-Marquez J E. Improving the computational efficiency of metric-based spares algorithms[J]. European Journal of Operational Research, 2012, 219(2): 324-334.
[18] van Horenbeek A, Scarf P A, Cavalcante C A V. The effect of maintenance quality on spare parts inventory for a fleet of assets[J]. IEEE Transactions on Reliability, 2013, 62(3): 596-607.
Configuration and Optimization Method of Carrying Sparesof Mission-oriented Combat Unit
RUAN Min-zhi1, FU Jian1, ZHOU Liang2, WANG Jun-long1
(1.Office of Research & Development, Naval University of Engineering, Wuhan 430033, Hubei, China;2.Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, Hubei, China)
Spare parts are important guaranty and basic material for a combat unit to ensure that the failure equipment can be put into combat and resumed to fight immediately. A calculation method for spares demand rate of redundant system based on equivalent life transformation is proposed. According to repairable spares inventory control theory, a carrying spares dynamic configuration model for multi-phase mission is established by taking with system mission success probability as objective function. Through the introduction of Lagrange constraint factors, a multi-constraint oriented spares optimization method is proposed. In a given example, the calculated result is analyzed, which meets all constraint conditions. The deviation between the calculated result and the ExtendSim simulation results is less than 3%. The correctness of the model is verified.
ordnance science and technology; mission-oriented; combat unit; carrying spares; dynamic optimization; redundant system
2016-11-11
武器装备“十三五”预先研究共用技术项目(41404050502)
傅健(1986—),男,硕士研究生。E-mail:462357912@qq.com
阮旻智(1983—),男,副教授,硕士生导师。E-mail:ruanminzhi830917@sina.com
E92
A
1000-1093(2017)06-1178-08
10.3969/j.issn.1000-1093.2017.06.018
