多目标优化的多品种维修器材分配问题研究

杨帆， 王铁宁

(装甲兵工程学院 技术保障工程系， 北京 100072)



多目标优化的多品种维修器材分配问题研究

杨帆， 王铁宁

(装甲兵工程学院 技术保障工程系， 北京 100072)

为了更好地满足部队维修器材需求，优化需求数量超过供应中心库存数的多品种维修器材分配整合供应问题，建立了保障重点、兼顾公平、效用最大的多目标优化模型。提出了采用灰色关联度方法对多目标进行处理，将多目标转化为单目标问题，并将之内嵌到改进遗传算法中。实例验证表明，该算法最优适应度值及平均适应度值可分别降低31.538 5%和37.371 1%，验证了该模型能有效减少器材分配失衡，提高器材供应效率。

兵器科学与技术； 维修器材； 多目标优化； 灰色关联度； 遗传算法

0 引言

部队的维修器材作为维修保障作业中至关重要的资源，对装备的维修及保障能力有着重大影响。当前部队维修机构对装备进行维修时，主要采取换件修理的方式，由此导致的大量维修器材的消耗就对部队维修器材库存控制和需求满足提出了很高的要求。如何对维修器材的库存范围进行合理控制，更好地满足部队维修需求，对我军的维修保障有着重要的意义。

部队维修器材的库存水平主要受订货、存储与供应影响。而决定部队维修器材库存水平的主要是器材订货决策及供应决策。传统的订货策略及供应策略主要是针对单品种器材，即每次仅对一个需求点进行供应，随着信息化程度的不断加深，信息共享条件下，器材供应保障系统的建设使得多品种供应方式得以发展[1]。多品种维修器材供应主要指整合供应方式，即供应中心向某需求点进行器材供应时，同时对该保障区域内的多个需求点的多种器材需求进行供应。多品种器材的整合供应，较传统的单一“请领- 供应”器材供应方式能够更好地降低成本，节约时间，满足部队需求。当前对多品种器材的联合订货策略研究已较为成熟[2-3]，而对多品种器材供应的研究仍然是一项十分迫切的任务。

本文主要研究供应中心器材数量有限时，多品种器材的分配问题。对多品种维修器材进行分配时，对部队任务性质、分配效用等均有要求，因此是一个多目标的优化问题。多目标优化是目前备受关注的一个重要问题，在车辆调度、生产设计、投资、生产调度领域等均有广泛应用。早期求解多目标问题时，一般通过加权求和等方式将多目标转化为单目标，再采用数学方法按单目标求解，但是求解效率低，且受权重的影响很大[4]。之后逐渐提出多目标优化的智能算法，如多目标进化算法NSGA2、SPE2等，运行效率较高，且可行解的分布良好，但是求解高维问题解集多样性缺陷较为明显[5]；多目标模拟退火算法对目标函数的要求很低，适应性较强，但是收敛速度慢、效率较低[6]；多目标蚁群算法和多目标遗传算法在全局空间的搜索能力较强，但是易出现停滞早熟问题[7]。因此，选择合适的方法，并针对所选方法的不足进行改进，应用于多品种维修器材分配的多目标优化，对于提高分配效率，保障维修需求有着显著意义。

本文建立了有限多品种维修器材分配的多目标优化模型，研究了同时对多需求点分配多品种器材时的约束条件，基于灰色关联度方法将多目标问题转化为单目标问题。将灰色关联度方法与遗传算法相结合，设计了灰色- 遗传优化求解方法。最后用10次仿真实例验证了该方法的可行性，为部队供应中心解决有限多品种器材分配问题提供一种新思路。

1 基于灰色关联度的模型构建

1.1 多品种维修器材分配模型构建

1.1.1 重点任务部队优先

在对各需求部队分配有限器材时，必须考虑各个需求点所执行任务的情况。对执行重点任务的部队，应该优先满足其器材需求。一般认为，若重点任务部队能分配得到的器材数量等于其请领上限，则该需求点部队器材需求得到满足。

(1)

式中：dj为需求部队的所属情况。

(2)

式中：Zij为第Sj个需求点对第Ri种需求上限的满足情况。

因此，该目标可以通过需求点某种器材得到完全满足的情况来衡量，即用执行重点任务的部队中被满足数量与总数之比f1来计算。

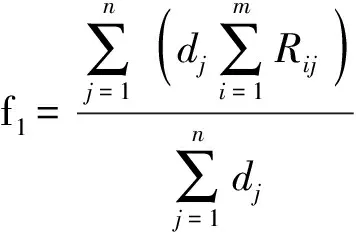
(3)

f1为多品种维修器材分配问题中考虑重点任务部队优先的一个目标，该目标越大越好。

同时，由于器材数量有限，不能完全保障所有需求得到满足，因此，对于执行重点任务的部队，其最低需求量必须得到满足，即

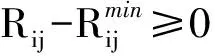
(4)

1.1.2 兼顾公平

在对各需求点进行器材分配时，由于总器材数有限，不可能满足所有需求点的需求上限。但是在对各需求点需求器材进行协调时，应该尽量秉持着公平原则，缩小分配过程中的不平衡。该目标用各个需求点部队满足率与平均满足率之间绝对差值f2大小来计算。

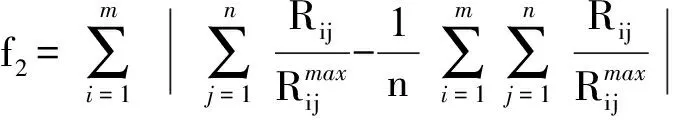
(5)

该目标值越小越好。

1.1.3 效益最大

多品种维修器材的合理分配问题，最重要的目标之一就是器材分配之后，考虑各个需求点获得的军事效益f3，即寻求所有需求点军事效益的最大化。效益最大目标就是从总体角度考虑，分析各个需求点在得到一定数量的维修器材之后，保障能力的大小，以此表征军事效益的大小，保障能力越高，则带来的军事效益越高，反之亦然。保障军事效益是考虑需求点在需求下限基础上所分配得到的超出下限的器材数量，该数量反映了在有维修需要时，需求点能够更好地满足装备维修保障需求的能力大小。

设对于需求点j，当收到某种数量的器材Rij时，其保障能力函数为uij(R1j，R2j，…，Rmj)。由于不同的需求部队重要性不同，因此，在考虑保障能力时，需要考虑各个需求点的权重wj，即得到每个需求点的效益函数qj为

qj=wjuj(R1j，R2j，…，Rmj).

(6)

由此可得归一化后效益函数Qj为

Qj(R1j，R2j，…，Rmj)=

(7)

(8)

式中：

(9)

(10)

该目标越大越好。

1.2 多目标优化设计的灰色关联度方法

由上述分析，可建立有限多品种维修器材分配的多目标模型。

s.t.

Qj(R1j，R2j，…，Rmj)=

1≤i≤m，1≤j≤n.

在得到多品种维修器材分配的多目标模型之后，通过灰色关联度方法，可将上述多目标问题转换为单目标问题。

设目标函数的参考序列为f0=(f01，f02，f03)；比较序列为f=(f1，f2，f3)。则f0与f的灰色关联度[8]为

(11)

式中：Δ(k)=|f0k-fk|，k=1，2，3；Δmax、Δmin分别为Δ(k)的最小值和最大值；ρ是介于0、1之间的分辨系数，一般取0.5。灰色关联度越小，表示比较序列与参考序列之间的差别越大，相似程度越小。f0与f的灰色相似系数μ[9]为

(12)

ε=αr+βμ,

(13)

式中：系数α≥0，β≥0，且α+β=1.

将多目标问题转化为求最小值问题的单目标问题进行求解，因此引入灰色差异度c：

c=1-ε.

(14)

c越小，表示比较序列与参考序列越接近，即结果越优。参考序列在寻优过程中动态取最小值即可，无需事先确定[11]。

2 基于灰色- 遗传算法的问题求解

2.1 编码

多品种的维修器材分配问题为离散整数问题，因此，在使用遗传算法进行编码时，为了提高运算效率和准确率，本文采用一维整数编码形式，表示各种器材分配给各个需求部队的数量。例如，假设有3种维修器材分配给3个需求点，则1个种群个体可以编码为(5，10，2，7，8，15，3，9，12)，前3个位置表示分配给第1个需求点的3种器材数量，中间3个位置表示分配给第2个需求点的3种器材数量，最后3个位置表示分配给第3个需求点的3种器材数量。

2.2 适应度函数

由于遗传算法对于约束条件的处理较为复杂，因此在根据灰色关联度方法转化的目标函数中，加入动态罚函数[12]来构造遗传算法的适应度函数F(Rij，δ)。

(15)

式中：δ为惩罚因子。随着迭代次数增加，越来越接近最优解时，动态惩罚因子也会随之越来越小。

2.3 最优个体保持策略

计算每个个体的适应度值，采用精英保留策略[13]，适应度函数值中最小的若干个体，即视为父代中的精英部分。该部分不进行交叉变异操作直接继承到子代。精英数目需要根据种群大小进行设定。除去精英个体之外的个体再按照设定的交叉与变异概率进行操作。例如种群大小为50，精英数目为3，则适应度值最小的3个染色体直接进入子代，剩下的47个染色体再进行交叉与变异操作。

2.4 遗传算子

采用轮盘赌法进行选择操作，计算个体的适应度值与种群总体适应度值的比值，将比值结果作为选择概率。由于本算法求目标函数的最小值，因此，比值越小的个体，被选择的概率就越大。

采用多点交叉的遗传算子，在染色体中随机选择3个切点，将第1与第2切点之间、第3切点之后的子串进行交叉[14]。变异操作时，从染色体中随机选择3个子点，在合理范围内，对该3个点进行替换，得到新的染色体序列。

3 实例仿真

文献[1]中对遗传算法进行改进后，采用各个目标加权求和方式求解多目标问题，并将改进算法与传统遗传算法进行对比。本文为了验证灰色- 遗传融合改进算法在解决多品种维修器材分配过程中多目标优化问题的优点，采用文献[1]给出的某防空旅的器材供应仿真实例进行验证，并把本文算法与文献[1]中列出的两种算法进行比较。实例验证程序如图1所示。

设该旅供应中心有3种维修器材A、B、C要分配给下属6个单位，每种器材的数量见表1.

表1 供应中心器材数Tab.1 Quantity of inventory materials in supply center

图1 实例验证流程图Fig.1 Flow chart of example verification

各单位的请领量和需求下界见表2.

表2 各需求点需求上下限Tab.2 Max and min demands of each demand point

表2中，单位2与单位5执行重点任务。从表2中可以看出，各单位请领总数大于供应中心现储器材数。因此需要对这些器材进行合理分配以最大化实现部队的保障需求。对于器材请领数小于供应中心可分配数的器材，直接按需分配即可，非本文研究内容。本文沿用文献[1]算法，对各个需求点的效用函数采用加权求和的形式，各个需求点对不同器材的权重及各个需求点部队自身的权重见表3.

由(9)式、(10)式可得单位1的最大效用和最小效用：

0.1×(0.4×0+0.25×2+0.35×1)=0.085，

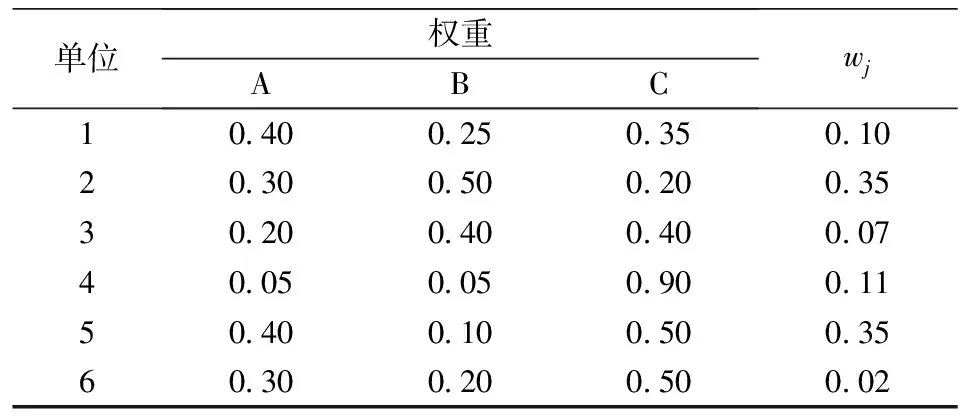
表3 器材及需求点权重Tab.3 Weights of materials and demand points

0.1×(0.4×20+0.25×65+0.35×20)=3.125.

同理，可求得各个需求点的最大效用和最小效用，见表4.

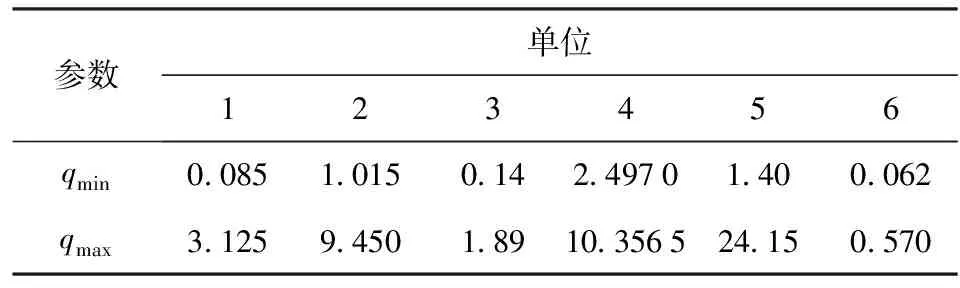
表4 各需求点最大和最小效用Tab.4 Maximum and minnimum utilities of each demand point

各单位获得一定数量的器材效用函数在仿真过程中，遗传算法的基本参数设置为：种群规模50，最大迭代数为50，精英保留数目为5，交叉概率为0.3，变异概率0.1. 在MATLAB 2014(a)环境下进行仿真运算。

为了验证算法可靠性，一共进行了10次实验，仿真适应度函数最优值及平均值如图2、图3所示。从图2、图3中可以看出，灰色- 遗传算法在求解多目标问题中，能够更快地找到最优解，并且优化过程比较平稳，而文献[1]遗传算法较之效率低。因为文献[1]仅仅是对交叉算子和变异算子进行简单改进，对于多目标向单目标的转化也只是进行简单的加权求和。将本文算法与文献[1]中列出的两种算法进行比较，3种算法的对比结果如表5所示。从表5中可以看出，灰色- 遗传算法与传统遗传算法及文献[1]中改进的遗传算法相比，能更很好地解决多品种维修器材分配的多目标优化问题。

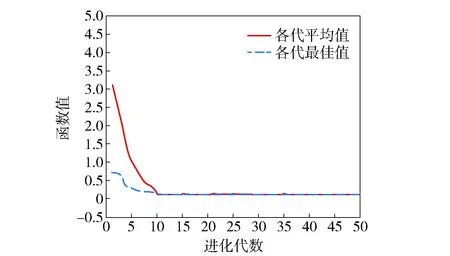
图2 本文算法结果Fig.2 Algorithm results in the present paper

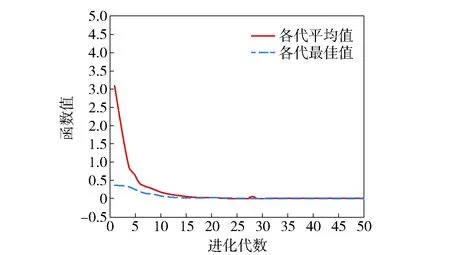
图3 文献[1]中改进的遗传算法结果Fig.3 Inproved GA algorithm results in Ref.[1]

表5 仿真结果比较Tab.5 Comparison of simulated results

计算可得，平均10次计算结果中，灰色- 遗传算法适应度最优值分别比文献[1]遗传算法和标准遗传算法小31.538 5%和97.050 5%，平均适应度函数值分别小37.371 1%和36.714 7%，优化了运算结果。最终器材分配结果见表6，与文献[1]结果相比，都能够保障重点部队与重点任务，同时，本文能够缩小各个需求点之间的分配不平衡性，较原分配方案有着更高的总体军事效益。

表6 器材分配结果Tab.6 Result of material distribution

4 结论

本文针对多品种维修器材分配的多目标优化问题，将灰色关联度方法内嵌到遗传算法模型中，提出了灰色- 遗传算法，并通过10次仿真实例进行验证。可以得出，该算法能够更好地解决多目标优化问题，提高维修器材分配的决策效率。灰色模型主要解决小样本问题，因此本文中模型的优点是对于小数据问题，能够进行高效准确地计算，而对于大规模数据的器材分配问题，需要在本文基础上，结合大数据的相关理论与方法做进一步的实验研究。

References)

[1] 聂成龙,张建荣.多品种维修器材库存决策优化技术[M].北京:国防工业出版社,2015. NIE Cheng-long, ZHANG Jian-rong. Inventory decision optimization technique of multi-item maintenance materials[M]. Beijing: National Defense Industry Press, 2015.(in Chinese)

[2] 刘亚东,孙志刚. 多品种维修器材统一订购策略的库存决策模型[J].火力与指挥控制,2013,38(1):133-137. LIU Ya-dong, SUN Zhi-gang. Inventory decision model of unanimous ordering policy with multi-item maintenance materials[J]. Fire Control & Command Control, 2013,38(1):133-137.(in Chinese)

[3] 张建荣,于永利,张柳,等. 维修器材联合订货的库存决策模型[J].系统工程与电子技术,2013,35(1):109-112. ZHANG Jian-rong, YU Yong-li, ZHANG Liu, et al. Inventory decision model of joint ordering policy with maintenance materials[J]. Systems Engineering and Electronics, 2013, 35(1):109-112.(in Chinese)

[4] 张迷,贺兴时. 多目标优化问题的花授粉算法改进[J].西安工程大学学报,2016,30(3):343-399. ZHANG Mi, HE Xing-shi. An improvement of flower pollination algorithm in multi-objective optimization[J]. Journal of Xi’an Polytechnic University, 2016,30(3):343-399.(in Chinese)

[5] Kundu P K, Zhang Y, Ray A K. Multi-objective optimization of simulated countercurrent moving bed chromatographic reactor for oxidative coupling of methane [J]. Chemical Engineering Science, 2009,64(19):4137-4149.

[6] 肖晓伟,肖迪,林锦国,等.多目标优化问题的研究概述[J].计算机应用研究,2011,28(3):805-827. XIAO Xiao-wei, XIAO Di, LIN Jin-guo, et al. Overview on multi-objective optimization problem research[J]. Application Research of Computers, 2011,28(3):805-827.(in Chinese)

[7] 兰世海.改进蚁群算法研究及其在车辆调度中的应用[D].上海:东华大学,2007. LAN Shi-hai. Study on improved ant colony algorithm and its application in the vehicle scheduling[D]. Shanghai: Donghua University, 2007.(in Chinese)

[8] Qin M Y, Liu D W, Luo Y S. Multi-objective optimization of turning parameters based on gray system theory[J]. Hydromechatronics Engineering, 2013,41(24):97-100.

[9] 扶名福,谢明祥,饶泓,等.基于综合关联度分析的风机故障诊断[J].中国机械工程,2007,18(20):2403-2405. FU Ming-fu,XIE Ming-xiang,RAO Hong,et al. Fault diagnosis of suction fan based on the synthetically relational analysis[J].China Mechanical Engineering,2007,18(20):2403-2405.(in Chinese)

[10] 韩朝晖,叶南海.混合离散变量的多目标优化设计灰色综合关联度算法[J].湖南农业大学学报:自然科学版,2008,34(4):495-497. HAN Zhao-hui,YE Nan-hai. Grey synthetically relational degree algorithm of multi-objective design with hybrid discrete variables[J].Journal of Hunan Agricultural University:Natural Sciences,2008,34(4):495-497.(in Chinese)

[11] 骆清国,尹洪涛,宁兴兴.一种基于有向图的冷却系统原理方案设计方法[J].兵工学报,2016,37(1):10-16. LUO Qing-guo, YIN Hong-tao, NING Xing-xing. A design method of cooling system principle scheme based on directed graph[J].Acta Armamentarii,2016,37(1):10-16.(in Chinese)

[12] 车晓毅,罗佑新,汪超. 高维多目标优化设计的灰色微粒群算法[J].机械传动,2009,33(1):55-58. CHE Xiao-yi, LUO You-xin, WANG Chao. Grey particle swarm optimal algorithm for high dimension multi-objective optimization design[J]. Journal of Mechanical Transmission, 2009, 33(1):55-58.(in Chinese)

[13] 郭惠昕,车晓毅,肖伟跃.混沌遗传优化算法及其在机械优化设计中的应用[J].机械设计,2003,20(10):23-25. GUO Hui-xin,CHE Xiao-yi,XIAO Wei-yue. Chaos-genetic optimal algorithm and application in mechanical optimal design[J].Journal of Machine Design, 2003,20(10):23-25.(in Chinese)

[14] 董朝阳,路遥,王青.改进的遗传算法求解火力分配优化问题[J].兵工学报,2016,37(1)：97-102. DONG Chao-yang, LU Yao, WANG Qing. Improved genetic algorithm for solving firepower distribution[J].Acta Armamentarii, 2016,37(1)：97-102.(in Chinese)

Research on Multi-objective Optimization of Multi-itemMaintenance Material Distribution Problem

YANG Fan， WANG Tie-ning

(Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

A multi-objective optimization model is established for multi-item maintenance material distribution to help the supply centers satisfy the maintenance material demands of troops. In the proposed model, the priority, fairness and efficiency are taken as the multi-objects. An improved genetic algorithm is combined with grey correlation degree method, which can transfer multi-objective problem to single-objective problem. The example verification shows that the best and mean fitness values are reduced by 31.538 5% and 37.371 1%, respectively. The proposed model can be used to reduce the unfairness of multi-item maintenance material distribution, and improve the efficiency of materials supply.

ordnance science and technology; maintenance material; multi-objective optimization；grey correlation degree；genetic algorithm

2016-11-04

军队科研计划项目(2016年)

杨帆(1990—)，女，博士研究生。E-mail：673729309@qq.com

王铁宁(1962—)，男，教授，博士生导师。E-mail：wtn0728@163.com

E92

A

1000-1093(2017)06-1186-06

10.3969/j.issn.1000-1093.2017.06.019