自主水下航行器回收过程中螺旋桨推力特性分析
2017-07-10杜晓旭张正栋
杜晓旭, 张正栋
(西北工业大学 航海学院, 陕西 西安 710072)
自主水下航行器回收过程中螺旋桨推力特性分析
杜晓旭, 张正栋
(西北工业大学 航海学院, 陕西 西安 710072)
在自主水下航行器 (AUV) 水下回收过程中,螺旋桨的推力特性对AUV的稳定性控制及安全性能等影响非常明显。主要基于计算流体力学方法,采用多块混合网格技术结合RNGk-ε湍流模型,对AUV在不同回收工况下的螺旋桨推力特性展开数值模拟。建立AUV及螺旋桨的三维几何模型;基于多块混合网格方法对计算域进行空间离散,同时采用动网格技术实现螺旋桨与回收管的相对运动及自身旋转运动;利用有限体积法展开数值计算。基于计算数据与试验数据的对比及数值无关性测试,表明所使用的多块混合网格方法能够对AUV回收过程螺旋桨推力特性进行准确计算,为AUV水下回收过程的控制及安全性能评估能够提供理论参考。
流体力学; 螺旋桨; 自主水下航行器; 多块混合网格; 推力特性
0 引言
自主水下航行器(AUV)作为水下自主航行的移动节点,目前在海洋各个领域中的用途愈加广泛。目前研究者们致力于AUV的水下自主回收研究,通常使用内径略大于AUV外径的管状回收装置实现AUV的回收[1]。AUV在回收过程中螺旋桨与回收装置之间的间隙随着AUV位置的不同而不同,从而导致该间隙流场变化十分剧烈,通常称这种复杂流场为极限流场。随着AUV向回收装置运动,螺旋桨由无界流场向极限流场运动,其推力特性受该流场的影响十分明显,推力特性的改变给AUV回收过程的稳定性控制带来了挑战,因此对该运动过程的螺旋桨推力特性研究十分有意义。
近年来随着计算机技术的推广普及和计算方法的新发展,计算流体力学(CFD)技术取得了蓬勃的发展,通过对雷诺平均N-S(RANS)方程的数值求解来获得黏性流场全场信息已经成为可能,因此CFD方法已经广泛应用到螺旋桨水动力特性研究中[2-4]。蔡荣泉等[5]基于非结构化网格对某五叶螺旋桨定常水动力性能进行CFD计算,计算结果与试验误差较小。解学参等[6]基于RANS方程和RNGk-ε湍流模型采用结构- 非结构多块混合网格研究了船后非均匀流场中螺旋桨的水动力性能,并将计算结果和试验结果比较,结果表明CFD计算方法精度较高,能够满足工程应用要求。Guo等[7]对不同轴深的螺旋桨展开数值模拟,并与试验结果对比,验证了数值模拟结果的准确性。苏石川等[8]基于两种网格(分区混合网格及非结构网格)研究某散货船螺旋桨敞水性能,对比发现分区混合网格误差较小。总之,采用CFD方法计算螺旋桨敞水水动力特性研究已相对成熟。
但是,目前采用CFD方法对螺旋桨水动力性能的研究主要集中在敞水性能方面,而AUV水下回收过程螺旋桨处于极限流域运动,且叶梢与管壁的间隙会随着AUV的运动而发生变化,因此螺旋桨所处流场极其复杂,其推力性能与敞水流域的推力性能有明显的差别。在上述过程中螺旋桨推力特性的改变对AUV的稳定性控制及安全性能都造成很大的影响,因此急需展开AUV水下回收过程螺旋桨推力特性的研究,为AUV水下回收过程的控制及安全性能评估提供定量的参考。本文基于CFD数值模拟方法,提出采用多块混合网格方法离散计算空间的计算方法,结合RNGk-ε湍流模型以及动网格技术利用有限体积法(FVM)研究不同回收工况下螺旋桨所产生的推力,分析上述过程对螺旋桨推力特性的影响,验证所提方法计算极限流场螺旋桨推力特性的准确性。
1 控制方程与湍流模型
1.1 控制方程
本文假设AUV在有界流场中航行时,周围流体为连续介质,为有黏不可压缩流体。由于螺旋桨叶梢与管壁之间的间隙时刻变化,因此桨叶周围流体视为不可压缩流体的三维非定常运动。因此满足控制方程[9]为
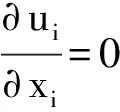
(1)
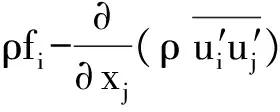
(2)
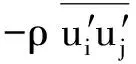
1.2 湍流模型
本文所采用的RNGk-ε湍流模型来源于严格地统计技术,它在ε方程中加了一个条件,从而有效地提高了精度。而且RNGk-ε湍流模型充分考虑了湍流漩涡对计算的影响,从而提高了其计算复杂旋转流场的精度。这些特点使得RNGk-ε湍流模型计算复杂流场有更高的可信度和精度。因此本文非定常湍流计算采用RNGk-ε双方程湍流模型使RANS方程封闭[9]。
湍流脉动动能方程(k方程)为

(3)
式中:αk为湍动能的有效普朗特数的倒数;μeff=μ+μt,μt为湍动黏性系数;Gk为由于平均速度梯度引起的湍动能;Gb是由于浮力影响引起的湍动能;YM为可压缩湍流脉动膨胀对纵耗散率的影响。
湍流能量耗散率(ε方程)为
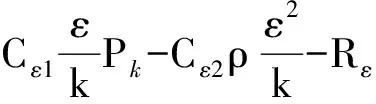
(4)
其中:
(5)
式中:Pk为湍动生成项;Rε与η为RNG湍流模型特有的控件;其他常数σε=1.39,Cε1=1.42,Cε2=1.42,Cμ=0.084 5,η0=4.38,β=0.012.
2 多块混合网格划分
2.1 几何模型
本文几何模型如图1所示,具体尺寸如表1所示。以AUV头部为原点建立参考坐标系,沿AUV向前运动轴向为x轴正方向,竖直向上为y轴正方向,根据右手准则确定z轴正方向,后文中的数值模拟计算均以AUV头部距参考坐标系原点距离为变量比较螺旋桨推力系数。
图1 几何模型示意图Fig.1 Schematic diagram of geometrical model

名称尺寸AUV外径/m02回收管长度/m3AUV长度/m185半锥角/(°)30螺旋桨直径/m0175
2.2 流场及网格划分
本文建立圆柱体流场计算域,长为29.85 m,直径为14 m. 流场计算域及边界条件设置如图2所示。入口边界条件为速度入口,出口设为压力出口,AUV及螺旋桨各壁面均设为无滑移壁面,采用标准壁面函数进行处理。计算域介质为水,密度ρ=1 024 kg/m3,其运动黏性系数为ν=1.003×10-6m2/s. 本文所选螺旋桨直径D=175 mm,定义螺旋桨推力系数为Ct=T/ρn2D4,T为螺旋桨产生推力,n为螺旋桨的转速,本文中n取900 r/min. 通过编制用户自定义函数(UDF)实现AUV及螺旋桨的自定义运动。
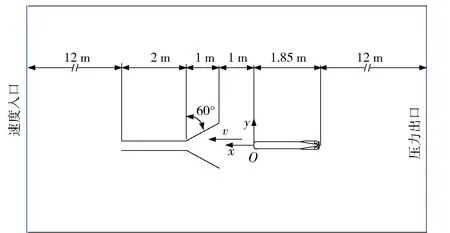
图2 流场计算域示意图Fig.2 Schematic diagram of calculation domain of flow fields
本文所用FVM进行数值求解具有良好的收敛性,能够满足计算需求。而采用FVM求解RANS方程实际是求解离散在计算域内各网格节点的流场信息,包括压力、速度以及湍流度等。因此合适的网格划分是偏微分方程准确求解的基础,也是数值模拟与分析的载体。划分合适的高质量网格在CFD数值计算中起着关键的作用,而网格的形状和精密度等对CFD计算的精度和计算效率有重要影响。目前网格划分主要分为结构网格和非结构网格,结构网格生成质量高但适应范围较窄,而非结构网格能够很好地适应不规则的几何模型,网格生成快,但是质量难以控制。针对两种网格的优缺点,分析本文的几何模型,考虑到本文流场的复杂性,使用单一的网格很难达到计算要求。于是本文采用结构网格和非结构网格相结合的多块混合网格方法对整个计算域进行划分,将流场分为静止域及运动域两部分,静止域为回收管以外部分,采用三维六面体结构化网格进行划分,运动域为回收管以内部分,动静域之间设立Interface交界面。将运动域分为两块,切出一个包含螺旋桨的圆柱部分,采用三维非结构化网格,而其余部分采用六面体结构化网格划分。
对于包含螺旋桨的圆柱部分采用非结构化网格划分,先用全三角形网格生成表面网格,再生成四面体网格填充计算域,在螺旋桨桨叶生成三棱柱边界层以更精确地捕获流场特性,同时对于螺旋桨桨叶部分进行加密,流场网格划分如图3、图4所示。
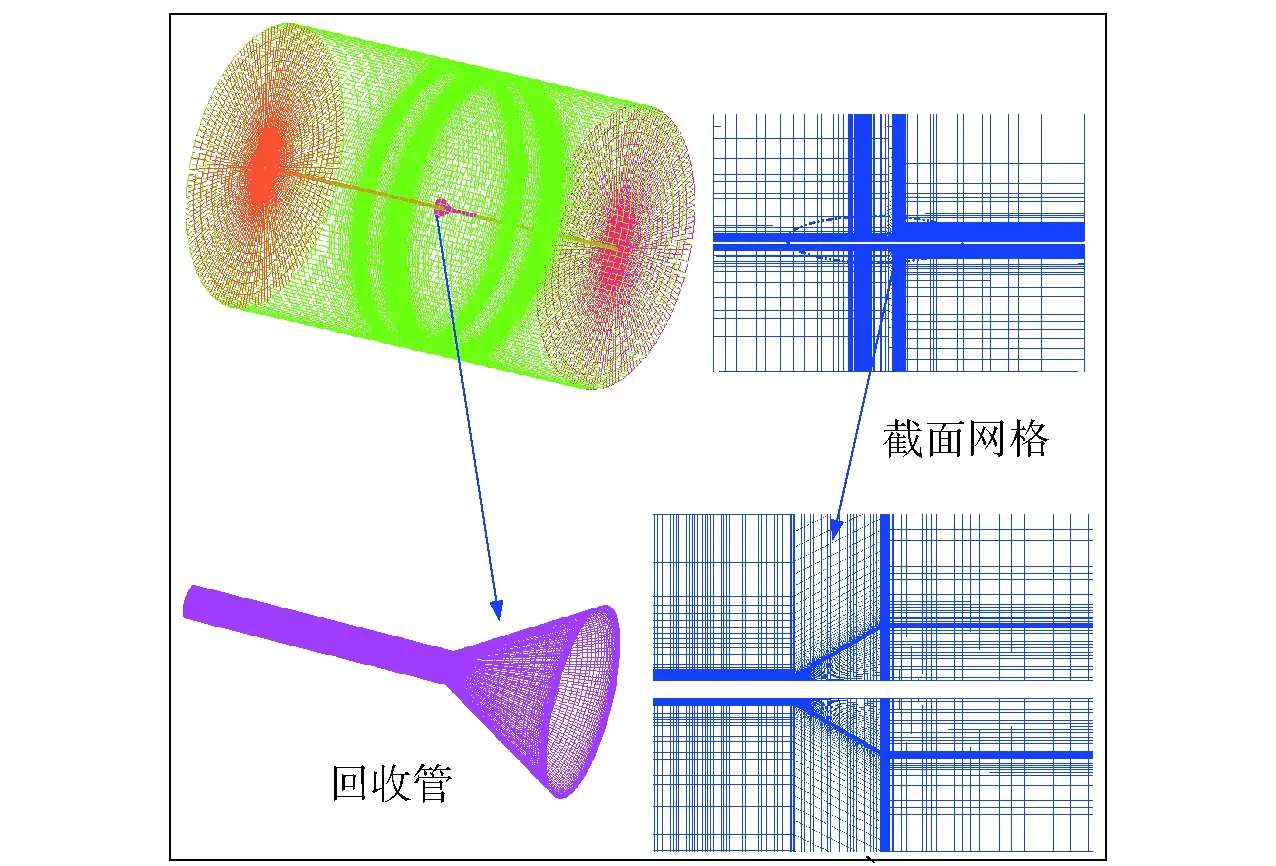
图3 静止域网格划分Fig.3 Meshes of stationary domain
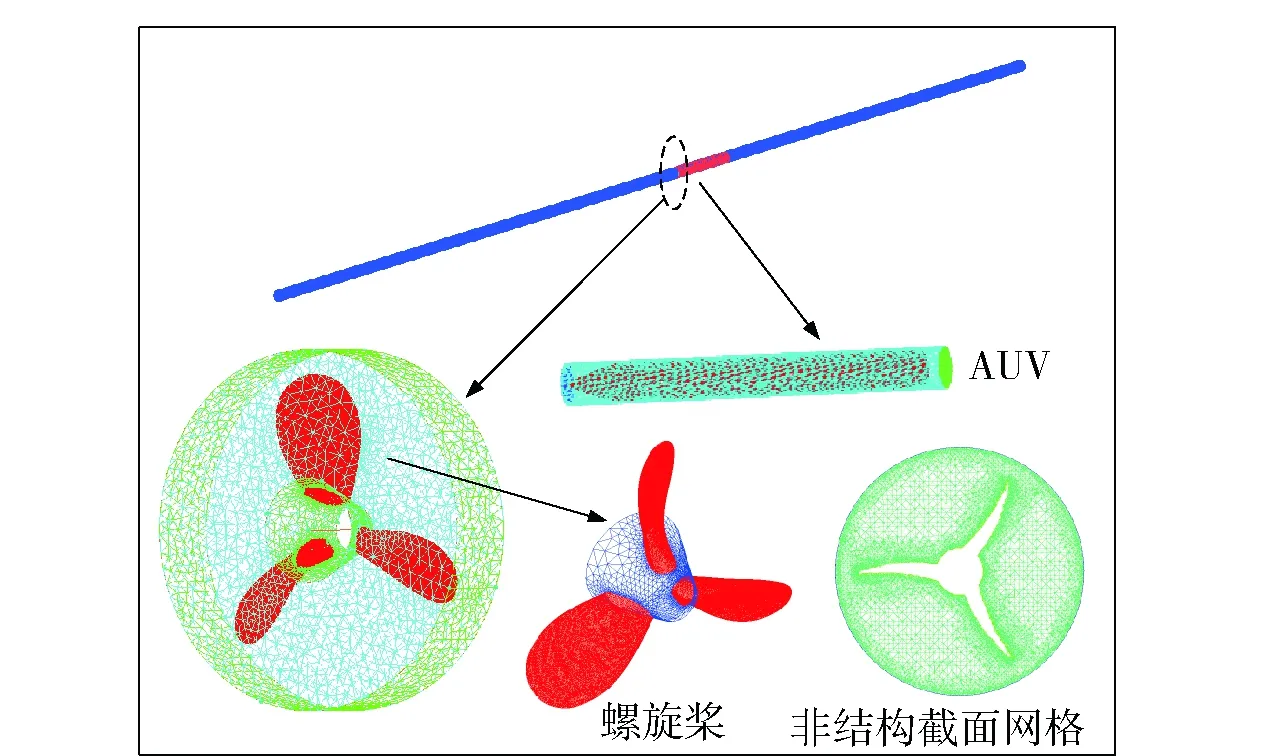
图4 运动域网格划分Fig.4 Motion domain meshes
3 数值计算结果及分析
3.1模型验证
在CFD计算中,网格的尺寸以及时间步长对计算结果的影响十分明显,为了验证计算的可靠性,分别对网格无关性以及时间步长无关性进行验证。本文将分别计算4种不同数量的网格的螺旋桨推力特性曲线,通过调节螺旋桨桨叶第1层网格尺寸、网格节点数目及最大网格尺寸等参数,分别得到252万、378万、504万以及756万网格,其对应的螺旋桨桨叶第1层网格尺度分别为0.01D、0.005D、0.001D,0.000 5D. 计算结果如图5(a)所示,随着网格数量的增多,螺旋桨推力系数曲线逐渐收敛,当网格数量为504万时,其计算结果与756万网格数量的计算结果几乎没有差别,于是认为504万的网格已达到网格无关,同时考虑到计算成本,因此本文取504万的网格作为计算网格。同时可以发现,当x<1.0 m时,螺旋桨推力系数保持不变,此时AUV与回收装置尚未接触,可以认为此时螺旋桨推力系数为敞水推力系数。本文所用螺旋桨根据日本MAU系列螺旋桨的图谱所设计[10],从文献[10]可看出在同进速系数下的螺旋桨试验推力系数KT=0.28,而此时本文推力系数数值模拟结果为Ct=0.300 2,相对误差不超过10%,可以认为数值模拟结果是准确的。如图5(b)所示为不同时间步长对螺旋桨推力系数的影响曲线,分别为0.05 s、0.01 s、0.005 s以及0.001 s. 从图5(b)中发现,随着时间步长的减小,推力系数曲线逐渐收敛。于是认为0.005 s的时间步长满足计算要求,后文计算中均取此时间步长。
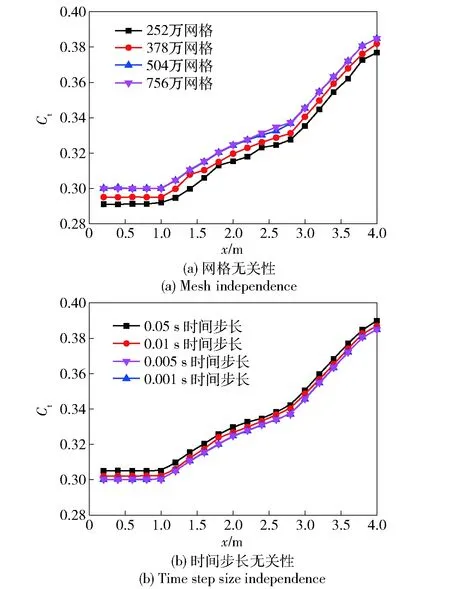
图5 网格及时间步长无关性对比结果Fig.5 Comparative results of mesh and time step size independence
3.2 AUV匀速进入回收管时螺旋桨推力特性
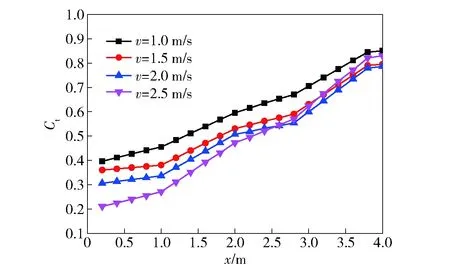
本节的回收管内径为220 mm,分别研究AUV以不同速度进入回收装置时的螺旋桨推力特性。本节分别对AUV以1.0 m/s、1.5 m/s、2.0 m/s、2.5 m/s 4种不同的速度进入回收管展开数值模拟,图6为AUV以不同速度进入回收管时螺旋桨推力特性曲线。
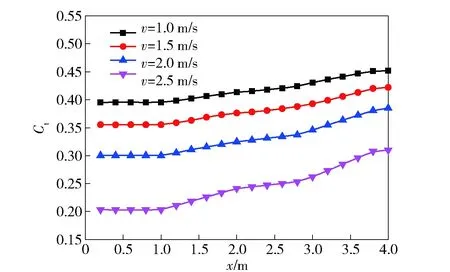
图6 AUV以不同速度进入回收管时螺旋桨推力系数曲线Fig.6 Propeller’s thrust coefficient curves when AUV enters the tube at different velocities
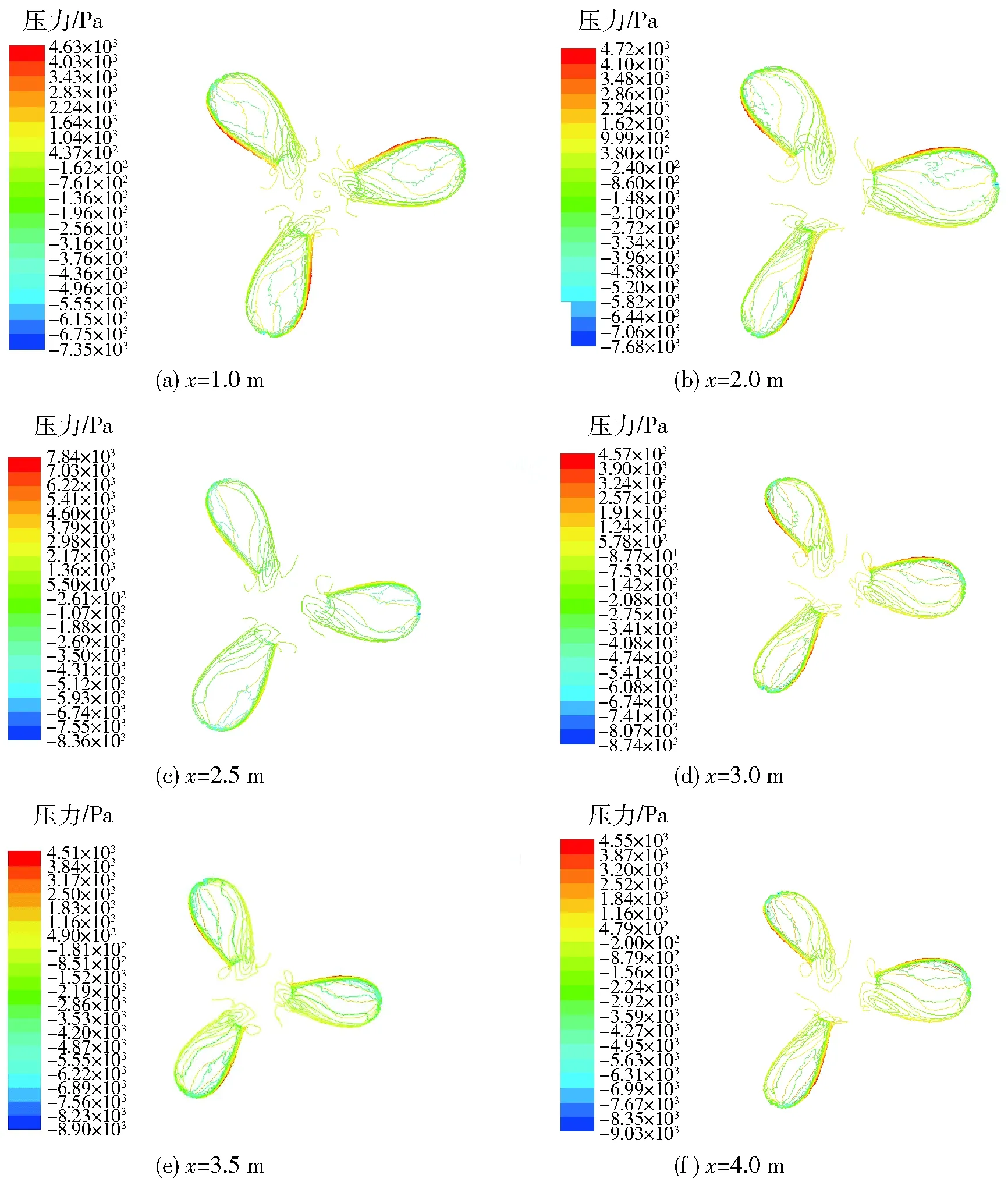
图7 不同位置处螺旋桨压力等值线图Fig.7 Propeller’s pressure contours at different positions
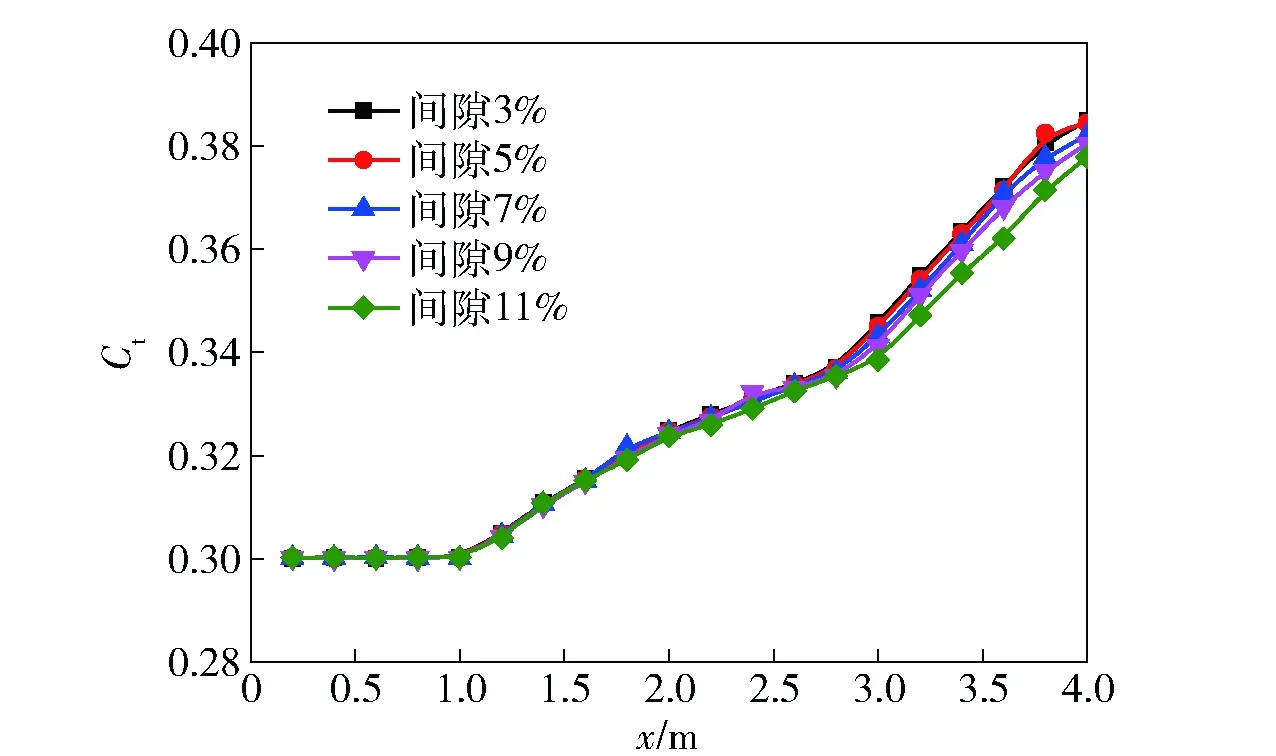
如图6所示,随着AUV完全进管,螺旋桨推力系数逐渐增大。当x≤1.0 m时,AUV头部尚未进入锥头,此时螺旋桨推力系数保持不变,这是由于螺旋桨与AUV均处于无界流域中,相对运动稳定;当1.0 m 图7为不同位置处的螺旋桨压力等值线图。由图7可以看出,在螺旋桨还未进入锥头时,叶片的导边处有较大的压力梯度,可知流体动力载荷分布在这里,而叶片的其余压力分布较为平缓,过渡均匀,上述叶片压力分布符合敞水流域螺旋桨叶片压力分布规律。随着AUV头部靠近锥头,流场出现干扰,流入盘面速度增加,产生的轴向诱导速度也逐渐增加,叶片与管壁之间的干扰使得压力分布变得更加不均匀,同时吸力面的最大压力下降,但是压力梯度明显上升,因此导致螺旋桨产生的推力上升。 如图8所示为AUV匀速进入回收管时在不同位置的切面速度云图,阴影部分为回收装置。当AUV还未进入回收管时,流场稳定,AUV及螺旋桨处于无界流场,螺旋桨推进特性不受回收装置的影响。当AUV头部刚要进入圆柱段时,回收装置里的水出现回流,同时一部分水沿着AUV与管壁间隙加速喷出,此时由于头部进管引起的流体加速逐渐开始影响螺旋桨盘面入口速度,导致螺旋桨推力系数开始增大。随着AUV头部进入回收管圆柱段,AUV与管壁的间隙流场逐渐影响到螺旋桨,螺旋桨产生的诱导速度变大,吸力面与压力面的压力梯度增大,导致螺旋桨产生的推力系数增大,这也与图6的螺旋桨推力系数变化趋势是一致的。 图8 AUV不同位置切面速度云图Fig.8 Velocity contours at different positions of AUV 3.3 AUV匀减速进入回收管时螺旋桨推力特性 在实际情况中,为了避免AUV与回收装置发生碰撞,AUV回收时的速度是逐渐减小的,本节对AUV以不同初始速度匀减速进入回收装置展开数值模拟,初始速度分别为1.0 m/s、1.5 m/s、2.0 m/s、2.5 m/s. 当x=4.0 m时,其速度降为0. 图9为AUV以不同初始速度减速进入回收管时螺旋桨推力特性变化曲线。 图9 不同初始速度对应的螺旋桨推力系数曲线Fig.9 Propellers thrust coefficient curves corresponding to different initial velocities of AUV 由图9可知,螺旋桨的推力系数变化规律与AUV匀速运动时几乎是一致的。当x≤1.0 m时,随着AUV向前运动,其运动速度线性减小,导致螺旋桨进速系数线性减小,推力系数近似呈线性增加,符合螺旋桨敞水推进特性规律;随着AUV进入回收装置,螺旋桨推力系数的增长速度变快。AUV速度越大,螺旋桨推力系数变化越明显,v=2.5 m/s所对应的螺旋桨推力系数,最终大于v=2.0 m/s及v=1.5 m/s所对应的推力系数。由此可见,AUV减速运动时,螺旋桨推力系数变化较之匀速运动时更加明显,极限流场对螺旋桨推力系数的影响也更加明显。 3.4 间隙对螺旋桨推力特性的影响 本节选用单侧间隙为3%、5%、7%、9%、11%的回收管模型进行数值计算,即回收管内径分别为212 mm、220 mm、228 mm、236 mm、244 mm,分别计算AUV以2.0 m/s的速度进入回收管时螺旋桨推力系数。图10为不同单侧间隙下AUV进入回收管时螺旋桨推力系数变化曲线。 图10 不同间隙下AUV进入回收管螺旋桨推力系数曲线Fig.10 Propeller’s thrust coefficient curves corresponding to different clearances between AUV and tube 图10表明,随着AUV进入回收管,AUV与回收管之间的间隙对螺旋桨推力特性的影响是非常明显的,尤其当螺旋桨进入锥头之后影响更为明显。当AUV处于回收装置之外时,间隙对螺旋桨推力系数的影响几乎为0,这也与实际流场是相符的。随着间隙的增大,间隙流场之间的干扰相对减小,从而螺旋桨的叶梢流场干扰相对减弱,从而引起推力系数的减小。同时可以发现当间隙大于7%的时候,螺旋桨推力系数有明显的下降趋势。 本文针对螺旋桨在AUV回收过程中处于极限流域这一复杂流场问题展开的数值模拟,基于螺旋桨桨叶较为复杂的几何外形,结合结构网格以及非结构网格的优点,提出了能够有效计算AUV回收过程螺旋桨推力特性的多块混合网格方法。同时结合动网格技术以及RNGk-ε湍流模型,形成了计算AUV回收时螺旋桨推力特性的计算方法。随后对计算域网格无关性以及离散时间步长无关性进行验证,提高计算精度。最后对AUV以不同速度匀速进入回收装置、不同初始速度匀减速进入回收装置以及不同间隙等工况下的螺旋桨推力特性进行计算。结果表明,这种基于多块混合网格方法计算AUV回收过程螺旋桨推力特性是可行的,而且对于极限流域的螺旋桨水动力特性研究具有普适性。 References) [1] 潘光, 黄明明, 宋保维. AUV回收技术现状及发展趋势[J]. 鱼雷技术, 2008, 16(6):10-14. PAN Guang, HUANG Ming-ming, SONG Bao-wei. Current situation and development trend of AUV recovery technology[J]. Torpedo Technology, 2008, 16(6):10-14. (in Chinese) [2] Funeno I. Analysis of unsteady viscous flow around a highly skewed propeller[J].Journal of Kansai Society of Naval Architects, 2002, 237: 39-45. [3] Bhattacharyya A, Krasilnikov V, Steen S. A CFD-based scaling approach for ducted propellers[J]. Ocean Engineering, 2016, 123:116-130. [4] 郑小龙, 黄胜, 王超. 基于CFD的螺旋桨定常水动力性能预报精度研究[J]. 舰船科学技术, 2014, 36(12): 11-15. ZHENG Xiao-long,HUANG Sheng,WANG Chao. Study of precision of steady hydrodynamic performance prediction of propeller of based on CFD[J]. Ship Science and Technology, 2014, 36(12): 11-15. (in Chinese) [5] 蔡荣泉,陈凤明,冯雪梅.使用FLUENT软件的螺旋桨敞水性能计算和分析[J].船舶力学,2006, 10(5): 41-48. CAI Rong-quan,CHEN Feng-ming,FENG Xue-mei.The use of FLUENT software of propeller open water perfomance calculation and analysis[J].Journal of Ship Mechanics, 2006, 10(5): 41-48.(in Chinese) [6] 解学参, 姜治芳, 邱辽原. 非均匀粘性流场螺旋桨非定常水动力性能研究 [J]. 船舶工程,2015, 37(6): 37-40. XIE Xue-can, JIANG Zhi-fang, QIU Liao-yuan. Research on unsteady hydrodynamic performance of propeller on non-uniform viscous flow fields[J]. Ship Engineering, 2015, 37(6): 37-40. (in Chinese) [7] Guo C, Zhao D, Sun Y. Numerical simulation and experimental research on hydrodynamic performance of propeller with varying shaft depths[J]. China Ocean Engineering, 2014, 28(2):271-282. [8] 苏石川,张力,魏承印. 基于不同网格类型的某散货船螺旋桨敞水性能预报与研究[J]. 江苏科技大学学报:自然科学版, 2016, 30(1):18-22. SU Shi-chuan, ZHANG Li, WEI Cheng-yin. Prediction of the open water performance of a bulk carrier propeller based on different grid types.[J] Journal of Jiangsu University of Science and Technology: Natural Science Edition, 2016, 30(1):18-22. (in Chinese) [9] 刘志华, 熊鹰, 叶金铭. 基于多块混合网格的RANS方法预报螺旋桨敞水性能的研究[J]. 水动力学研究与进展, 2007, 22(4): 50-56. LIU Zhi-hua, XIONG Ying, YE Jin-ming. Study on the prediction of propeller open-water performance using RANS formula and multi-block hybrid meshes[J]. Journal of Hydrodynamics, 2007, 22(4): 50-56. (in Chinese) [10] 盛振邦, 刘应中. 船舶原理(下)[M].上海:上海交通大学出版社, 2004. SHENG Zhen-bang, LIU Ying-zhong. Ship theory (2) [M]. Shanghai: Shanghai Jiao Tong University Press, 2004. (in Chinese) Analysis of Propeller Thrust Performance in the Process ofAutonomous Underwater Vehicle Recovery DU Xiao-xu, ZHANG Zheng-dong (School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, Shaanxi, China) The influence of propeller thrust performance on the stability control and safety performance of autonomous underwater vehicle (AUV) during the process of AUV recovery is very obvious. Based on CFD method, the multi-block meshes method combined with RNGk-εturbulent model is used for the simulation of propeller thrust performance of AUV in different recovery cases. The three-dimensional geometric models of AUV and propeller are built. The calculation domain is dispersed by multi-blocks meshes, and the dynamic mesh technique is used to simulate the motion of AUV and propeller. The numerical simulations are performed based on the finite volume method. The comparison of numerical and experimental results,as well as numerical independence test show that the proposed numerical method can be used to calculate the propeller thrust performance during the process of AUV underwater recovery accurately, and the numerical results can provide theoretical reference to the stability control and safety performance of underwater AUV recovery. fluid mechanics; propeller; autonomous underwater vehicle; multi-blocks mesh; thrust performance 2016-10-18 国家自然科学基金项目(1130276) 张正栋(1993—),男,硕士研究生。E-mail:18789496770@163.com 杜晓旭(1981—),男,副教授,硕士生导师。E-mail:nwpudxx@163.com U661.31+3 A 1000-1093(2017)06-1154-07 10.3969/j.issn.1000-1093.2017.06.015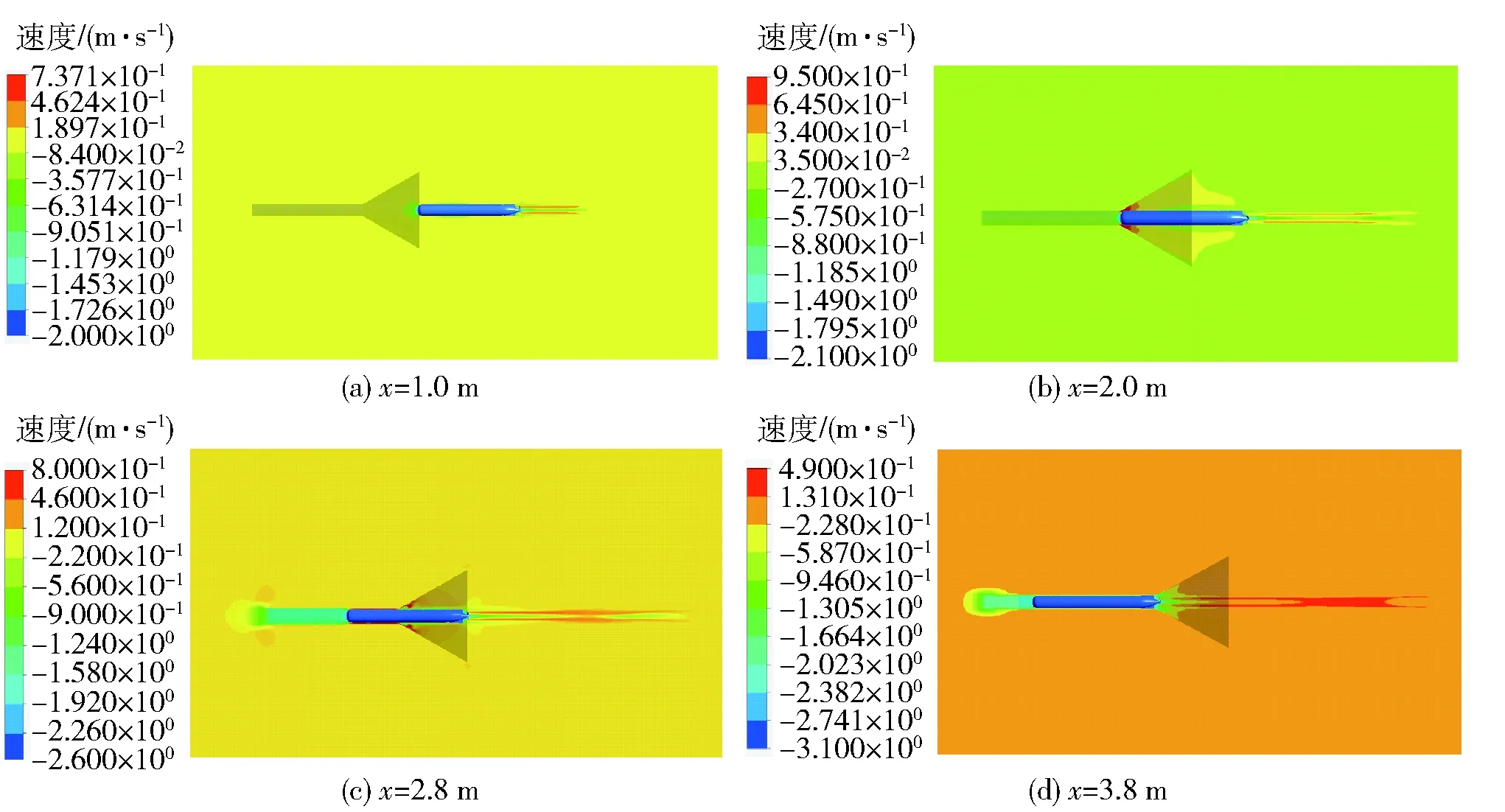
4 结论
