面向海底光学探测使命的自治水下机器人水平路径跟随控制

马艳彤， 郑荣， 韩晓军

(1.中国科学院 沈阳自动化研究所 机器人学国家重点实验室， 辽宁 沈阳 110016；2.东北大学 机械工程与自动化学院， 辽宁 沈阳 1108191)

面向海底光学探测使命的自治水下机器人水平路径跟随控制

马艳彤1,2， 郑荣1， 韩晓军1

(1.中国科学院 沈阳自动化研究所 机器人学国家重点实验室， 辽宁 沈阳 110016；2.东北大学 机械工程与自动化学院， 辽宁 沈阳 1108191)

针对利用光学探测设备对海底目标探测与搜索的使命，自治水下机器人(AUV)需具备更精确的航行控制性能，为此提出一种不依赖模型的改进型PID控制算法，通过对增设的左右水平推进器进行控制，以实现AUV低速时水平面的精确航行。将整个控制器分为两层：内层为偏航距离PID控制器，将输出量转化为所需偏转角；外层为航向PID控制器，将内层计算结果转化为航向偏差，对其进行PID计算，输出为偏转所需推力和推力矩值。通过对设定探测路线进行路径跟随，以反映水平面航行控制精度。通过湖上试验，得出精确的路径跟随航迹，实现了航向角偏差均值为0.09°、航向距离偏差均方差为0.29 m的航行稳定控制，验证了该控制方法的可行性。

控制科学与技术； 自治水下机器人； 海底光学探测； 改进型PID； 路径跟随； 水平推进器

0 引言

目前，利用自治水下机器人(AUV)搭载探测设备完成海底高精度探测和微小目标识别的需求日益强烈，而海底探测手段主要为声学探测设备。但声学存在诸多局限性，如声纳成像的像素信息少，近距离探测时易受环境噪声和目标背景物的干扰等[1-2]。与声学探测设备相比，光学设备则具有分辨率高、信息丰富的特点，但成像范围较小，仅适用于米级的精确探测[1,3]。因此，若采用光学探测设备完整、高效地完成指定区域的目标探测与识别，则要求AUV具备良好的近底定高稳定航行性能，包括：稳定的高度和俯仰控制，以满足海底近距离探测的需求；精确的分米级精度的路径跟随性能，即要求航行体航向偏差小和转弯性能稳定，以实现在指定区域的全覆盖、无缝探测与目标搜索。对于前者，郑荣等[4]已实现了AUV垂直面稳定的近底定高航行，能够很好地满足要求，具体参见文献[4]。因此，本文的重点是AUV水平面的精确路径跟随控制研究。

AUV的水下航行是一个复杂的空间六自由度运动，本身具备强耦合性和高度非线性，难以建立精确的数学模型，这使得AUV的精确航行控制问题非常复杂。对此，国内外研究学者提出了多种智能算法。文献[5-8]采用李亚普诺夫稳定性理论和反步法设计了欠驱动AUV的路径跟随控制；文献[9]针对传统直线航迹控制力矩方法较为复杂的问题，提出基于级联系统理论的控制力矩设计方法；文献[10]提出自适应模糊反演滑模控制系统设计，以解决AUV水平面航迹跟踪问题；文献[11]针对AUV为多输入多输出系统特性，提出自适应模糊PID控制算法，用于AUV航向控制，以解决PID参数整定的不确定性问题。以上这些算法在仿真时实现了精确的路径跟随控制，验证了其理论的可行性，但并未经过实际航行试验的检验，且以上这些航迹跟踪控制算法对AUV的运动、动力模型精度要求较高，具有较强的模型针对性。对于载体模块化的AUV，由于其可根据不同需求加载不同载荷，使得模型并不固定。因此基于模型的控制算法难以在工程上很好地应用于模块化AUV。而PID控制算法具有原理简单、使用方便、应用广泛、鲁棒性强等优点，可实现不依赖对象模型的控制，被广泛用于AUV工程实践中。国内外广泛采用航向单闭环PID对AUV进行路径跟随控制，但航线偏差较大，路径跟随的控制精度难以满足应用要求[12-13]。文献[14]提出了基于双闭环的矢量推进器的AUV路径跟随，做到了10 m以内的航线偏差控制，其精度仍不能满足光学探测需求。

基于以上问题，本文在传统PID控制的基础上进行改进，提出双层PID的控制算法，即通过双层PID嵌套，控制AUV的航向偏差和转弯稳定性，以实现AUV水平面精确路径跟随控制。另外，为保证光学摄像机的成像效果，将AUV巡航探测速度设为1 kn以下。为解决低速下舵效不足[15]的问题，在载体重心左右对称位置设置左右水平推进器。在此基础上，通过湖上试验验证该控制方法的可行性。

1 问题描述

所谓路径跟随，是指为控制器设计一个控制输入，使AUV能够从给定的初始状态出发，到达并跟随指定坐标系下给定的参考路径，而对到达目标位置的时间不做要求[16]。尽管AUV的实际水下航行为三维空间运动，但为突出研究重点，本文不讨论航行体的深度控制，且忽略横滚的影响，主要研究AUV水平面的路径跟随控制问题。

1.1 设定路径描述

为实现对指定区域的全覆盖探测与搜索，巡航路线应尽量密集。本文设计的“织网”式巡航路线，即在指定区域回纹穿梭航行，每条航线之间的距离略大于光学设备的视场宽度。“织网”式巡航路线如图1所示。

图1 “织网”式行进航线Fig.1 “weaving” cruise route

航行体按照：起点-1-2-3-…-16-a-b-c-…-h-终点的“套圈”式航行。每条航线间距5 m，通过东西向和南北向的交叉，可实现行进区域的全覆盖搜索。同时，该航线的设计能够很好地验证航行体直航阶段的航向偏差控制和转弯的转向控制。在直航阶段，航向偏差可作为衡量其精确路径跟随的稳定性指标；在转弯阶段，转向性能主要体现在转弯半径的稳定控制。

1.2 航行误差分析

为便于问题描述，根据国际水池会议(ITTC)和造船与轮机工程学会(SNAME)术语体系，在水平面内建立两种坐标体系：固定坐标系Εηξ为惯性坐标系；运动坐标系OXY，将原点选在AUV重心处，为载体坐标系。在此坐标体系下分析航行体的路径跟随情况。

1.2.1 直航误差分析

图2 直航阶段路径跟随示意图Fig.2 Schematic diagram of AUV straight path following

1.2.2 转弯误差分析

由于航行体受水流和自身惯性影响，无法做到直角转弯，其实际航线会呈弧线形。本文通过控制其实际的转弯半径来控制每条航迹间距离。根据前面的航线设计，为保证每条航线间距为5 m，此处应实现航行体转向稳定且转弯半径在2.5 m附近。其转向示意图如图3所示。

图3 转弯示意图Fig.3 Schematic diagram of AUV steering

2 水平面路径跟随航行控制

在水平面航行控制中，航行体的前向推力由主推进器提供，转向力和力矩由左右水平推进器提供。针对实际航迹与目标航线偏差，设计控制器，以实现对设定航线的精确路径跟随控制。即由控制器控制左右水平电机转速调节航线偏差和驱动转弯。

2.1 双层PID控制器设计

AUV在水下航行过程中偏离目标航线时，按照偏航角φe和偏航距离l可将出现航向偏差的情形分为3种(见图4)。

图4 航向偏差示意图Fig.4 Schematic diagram of course deviation

传统的PID控制器多是航向单闭环PID控制器，即是将航向角偏差作为PID误差反馈因子，在控制策略上未考虑由距离偏差造成的航线偏差问题，不能精确地实现路径跟随控制。因此，本文在航向角PID控制的基础上，改善控制策略，将距离偏差引入到控制器中，采用双层PID控制。即将航向角偏差和距离偏差作为反馈量同步关联到航线调整中。另外，直接将AUV航向调整所需推力作为控制器的输出量，以实现精确的路径跟随控制。双PID控制框图如图5所示。图5中：θp为要偏转的角度；θt为目标航向角；Ht为目标航向；H为当前航向；e为航向偏差。

图5 双层PID控制框图Fig.5 Block diagram of bilayer PID control strategy

2.2 控制器算法实现

整个控制器由两部分组成：第1部分为内层PID控制器，用于计算所需偏转角，即对偏航距离进行PID处理，将输出定为所需偏转角；第2部分为外层PID控制器，用于计算AUV航向调整所需推力和推力矩，即将内层PID计算结果转换为目标航向，与实际航向偏差作为反馈因子，PID处理后将输出作为推力和推力矩。

2.2.1 航向角偏差计算

如前面所述，当出现航向偏差时，航行体实际位置与设定路线存在一定距离l，通过l计算航行体所需偏转角度。其中l由AUV导航系统给出。

这里根据l的大小采用分段PID算法，具体调节过程为

l<10 m时，

(1)

l>10 m时，

θp=K′·l.

(2)

式中：lm表示第m个积分量；lk表示第k个微分量；T为采样周期；Kp，θp、Ki,θp、Kd,θp为偏航角PID参数；K′为比例放大因子，可通过多次试验获得其准确值。

2.2.2 转向控制

计算出所需偏转角后，可由目标航向角计算出目标航向，再通过目标航向与当前航向的比较，得出航向偏差，其计算公式为

Ht=θt-θp，

(3)

e=Ht-H.

(4)

通过控制算法，求出AUV对应的转向所需转矩的控制量M，此处按航向偏差e大小进行分段控制：

式中：Kp、Ki、Kd为航向PID参数；Kδ为比例增益，可通过多次试验获得其准确值。以上参数均针对航行体具体转向性能而定。如若实现转弯半径，调整控制参数即可。

由于采样周期较短，微分项会产生较大的噪声信号，影响控制效果，因此这里采用最小二乘法对角速度进行滤波平滑，以期获得较好的控制效果[17]。

求出转向力矩后，可计算出分配给左右推进器的转向力为T=M/L，L为左右推进器距载体中轴线距离。计算出左右推进器转速大小相等，方向相反。以此实现航行体的转向控制。

本文中，推进器螺旋桨转速与力的函数关系式采用参数辨识的方法获得，具体不再赘述。

AUV航线偏差调整的控制流程图如图6所示。

图6 AUV航向控制流程图Fig.6 Flow chart of AUV course control

本文设计的双层PID控制器完全独立于控制模型。即无需对模型进行复杂的运动学、动力学分析，只需根据控制要求调整PID参数，即可实现控制器对模型的运动控制。

3 试验结果分析

本试验用AUV长度9.5 m，直径为534 mm，空气中净质量1.5 t，最大下潜深度为200 m，左右推进器最大转速为1 800 r/min，其外形结构和左右推进器布放位置如图7所示。在某湖泊进行了AUV的湖上试验，设定航速为v=0.514 m/s. 通过试验验证航行体在低速下水平面路径跟随控制方案的可行性。

图7 AUV外形结构俯视图Fig.7 Top view of AUV shape structure

本文针对航行体在不考虑垂向高度和纵倾变化的情况，分析其水平面的航行控制稳定性。将设定的“织网”式回纹行进航线作为目标航线。将实际航线与目标航线分析比较，得出AUV的路径跟随性能。这里主要对航向角偏差、转弯角速度和转弯半径稳定性进行分析。同时，由于为实现低速下航向偏差调整和转弯的精确控制，增设了左右水平推进器，为此对其控制进行分析，以验证推进器对航行体的驱动控制性能。

3.1 偏航误差分析

受多种因素影响，AUV在航行中，会偏离设定航线。通过实际航向与目标航向的数据比较，可得出航向角偏差。通过试验，验证偏航误差的调整和稳定性控制性能。试验结果如图8所示。

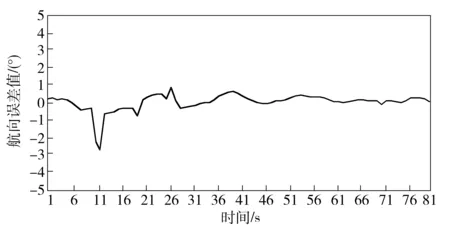
图8 航向误差曲线Fig.9 Curve of AUV course deviation

从图8中可以看出，航行体在航行至11 s附近出现了航向偏差，但随后通过控制算法的调节，航向误差值逐渐减小，最终在45 s附近趋于稳定，且航向偏差稳定在零值附近，均方差为0.09°，表明该控制系统的准确性与快速响应性。

3.2 转弯稳定性分析

3.2.1 转弯角速度稳定性

水平转弯角速度ω由AUV上的惯性组合导航模块采集得到。图9为一组典型实航时转弯角速度数据曲线。从图9可以看出，水平角速度波动小，转向平稳。验证了PID算法控制转弯角速度的可行性与控制的精确性。

图9 转弯角速度曲线Fig.9 Curve of AUV turning angular velocity

3.2.2 转弯半径稳定性分析

由于转弯半径无法通过传感器直接采集，需对其进行计算。转弯半径r由弧长的计算公式推导得出：

(6)

式中：s为转弯走过的弧长，由惯性组合导航单元与多普勒计程仪共同测得；Δt为转弯航段所用时间。

表1为航行体在不同转弯航段下的转弯半径。从试验结果可以看出，转弯半径稳定在2.5 m附近，表明了转向控制的精确性和稳定性。其中，南北航向均方差为0.099 m，东西航向转弯半径均方差为0.067 m，波动很小，表明方向的改变对转弯半径的大小和稳定性影响很小。

表1 AUV不同航段下转弯半径Tab.1 AUV turning radii at different time

3.3 左右推进器驱动控制分析

AUV的精确转向是通过PID控制左右推进器转速实现的。通过不同的推进器转速来调整相对应的航向偏差。

图10反映了直航阶段航向偏差调整时，航向角误差和左右推进器转速的变化关系。由图10可以看出：左右电机转速随着航向偏差变化而变化，当航向误差增大时，左右推进器转速快速增加，以调节航向偏差值；同样，当航向误差减小时，转速变低，很好地验证了PID算法的准确性和快速响应性。

图10 航向偏差与电机转速关系曲线Fig.10 Course deviation vs. motor speed

图11反映了转弯阶段航向角和左右推进器转速的变化关系。由于转弯时，航向角变化较大，通过转向算法可知，当航向角大于15°时，左右推进器转速达到最大值，以实现快速平稳地转向。

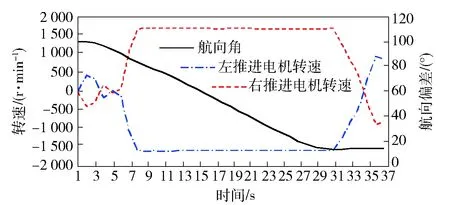
图11 转弯时电机转速Fig.11 Motor speed when turning

图12为AUV实际的航迹和设定航线对比图，其中实线为实际航迹，虚线为设定航线。该设定航线即为前面所述的间隔为5 m的“织网”式巡航路线。

图12 AUV实际航迹和设定航线对比图(实线为实际航迹，虚线为设定航线)Fig.12 Comparison of AUV actual tracking and set routes (solid line: actual path; dotted line: set path)

由图12可以看出，实际航迹能够很好地跟随设定航线，主要体现在：其水平角速度均方差为0.131°/s；转弯半径稳定在2.5 m；偏航角均值为0.09°；偏航距离均方差为0.29 m，实现了精确的分米级路径跟随。

4 结论

本文针对AUV搭载水下光学探测设备进行目标探测时航行控制精度要求高的问题，提出采用双层PID控制算法。并通过湖上试验对该控制方案的可行性进行了验证，在对试验结果进行分析后，可得出以下结论：

1)利用左右水平推进器提供航行体低速下的转向驱动力，通过双层PID控制器实现了精确的航向偏差调整和转弯稳定性控制。

2)该控制方案提高了路径跟随的控制精度，实现了AUV分米级跟随，满足AUV搭载光学设备高效精细探测海底的要求。

References)

[1] 徐玉如, 李彭超. 水下机器人发展趋势[J]. 自然杂志, 2011, 33(3):125-132. XU Yu-ru, LI Peng-chao. The development of underwater robots[J]. Chinese Journal of Nature, 2011, 33(3):125-132.(in Chinese)

[2] Fillinger L, Hunter A J, Zampolli M, et al. Passive acoustic detection of closed-circuit underwater breathing apparatus in an operational port environment[J]. Acoustical Society of America, 2012, 132(4):310-315.

[3] 孙传东, 陈良益, 高立民. 水的光学特性及其对水下成像的影响[J]. 应用光学, 2000, 21(4):39-46. SUN Chuan-dong, CHEN Liang-yi, GAO Li-min. Water optical properties and their effect on underwater imaging[J]. Journal of Applied Optics, 2000, 21(4):39-46. (in Chinese)

[4] 郑荣, 马艳彤, 张斌. 基于垂向推进方式的AUV低速近底稳定航行[J]. 机器人, 2016, 38(5):588-592. ZHENG Rong, MA Yan-tong, ZHANG Bin. AUV’s near-bottom and low-speed sailing stability control based on vertical thruster[J]. Robot, 2016, 38(5):588-592. (in Chinese)

[5] Lionel L,Didik S. Nonlinear path-following control of an AUV[J]. Ocean Engineering, 2007, 34(11/12):1734-1744.

[6] Silvestre C, Pascoal A. Control of the INFANTE AUV using gain scheduled static output feedback[J]. Control Engineering Practice, 2004, 12(12):1501-1509.

[7] Repoulias F, Papadopoulos E. Planar trajectory planning and tracking control design for underactuated AUVs[J]. Ocean Engineering, 2007, 34(11/12):1650-1667.

[8] Bidyadhar S. Debabrata A. Design of a path following controller for an underactuated AUV[J]. Archives of Control Sciences, 2009, 19( 3): 245-259.

[9] Khodayari M H, Balochian S. Modeling and control of autonomous underwater vehicle (AUV) in heading and depth attitude via self-adaptive fuzzy PID controller[J]. Journal of Marine Science and Technology, 2015, 20(3):559-578.

[10] 付江锋, 严卫生, 赵涛. 欠驱动AUV的直线航迹跟踪控制[J]. 计算机仿真, 2009, 26(10):145-147. FU Jiang-feng, YAN Wei-sheng, ZHAO Tao. Line tracking control of underactuated AUV[J]. Computer Simulation, 2009, 26(10):145-147. (in Chinese)

[11] 万磊, 崔士鹏, 张国成, 等. 欠驱动水下机器人航迹跟踪控制[J]. 电机与控制学报, 2013, 17(2):103-110. WANG Lei, CUI Shi-peng, ZHANG Guo-cheng, et al. Path following control of underactuated autonomous underwater vehicles [J]. Electric Machines and Control, 2013, 17(2):103-110. (in Chinese)

[12] Wang B, Su Y M, Wan L, et al. Adaptive PID control system for an autonomous underwater vehicle[J]. High Technology Letter, 2011, 17(1):7-12.

[13] Chen Q, Chen T, Zhang Y. Research of GA based PID for AUV motion control[C]∥Proceedings of the 2009 IEEE International Conference on Mechatronics and Automation.Changchun: IEEE, 2009:4446-4451.

[14] 陈世利, 卫民, 李一博. 基于双闭环的矢量推进器的AUV 转向控制方法[J]. 天津大学学报:自然科学与工程技术版, 2014, 47(6):530-534. CHEN Shi-li, WEI Min, LI Yi-bo. Steering control strategy of AUV with vectored thruster based on double-loop mode [J]. Journal of Tianjin University :Science and Technology, 2014, 47(6):530-534. (in Chinese)

[15] 晏亮, 赵琳, 程建华. 潜艇操纵运动的舵效仿真研究[J]. 计算机仿真, 2009, 26(7):12-15. YAN Liang, ZHAO Lin, CHENG Jian-hua. Rudder effects simulation of submarine maneuvering motion [J].Computer Simulation, 2009, 26(7):12-15. (in Chinese)

[16] 王芳, 万磊, 李晔. 欠驱动AUV的运动控制技术综述[J].中国造船, 2010, 51(2):227-241. WANG Fang, WAN Lei, LI Ye. Asurvey on development of motion control for underactuated AUV[J]. Shipbuilding of China, 2010, 51(2):227-241. (in Chinese)

[17] 刘健, 于闯, 刘爱民. 无缆自治水下机器人控制方法研究[J].机器人, 2004, 26(1):7-10. LIU Jian, YU Chuang, LIU Ai-min. Research on untethered autonomous underwater vehicle control method[J]. Robot, 2004, 26(1):7-10.(in Chinese)

Horizontal Trajectory Tracking Control of Autonomous UnderwaterVehicle Based on Seabed Optical Detection Mission

MA Yan-tong1,2， ZHENG Rong1， HAN Xiao-jun1

(1.State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences,Shenyang 110016, Liaoning, China;2.School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, Liaoning, China)

Autonomous underwater vehicles (AUVs) need to be provided with more accurate navigation control due to the limited operating range of optical detection device for detecting the seabed. An improved bilayer PID control algorithm which is independent of the object model is proposed. By controlling the channel propellers which are retrofitted to flanks around AUV, the controller can achieve AUV precise navigation control at low speed. The controller consists of two layers: the inner layer is a PID controller for distance deviation computation, which converts the output to desired deflection angle; the outer layer is a PID controller which computes the desired thrust and torque by inputting the output value of inner layer. The horizontal navigation precision can be reflected by tracking the planned detection route. The precise tracking path was obtained in lake trial. The mean value of course angular deviation is 0.09 °, and the mean square errors of deviation from the course is 0.29 m, which verifies the feasibility of the control scheme.

control science and technology; autonomous underwater vehicle; seabed optical detection; improved PID; trajectory tracking; horizontal propeller

2016-10-11

中国科学院国防科技创新基金项目(CXJJ-16M221)

马艳彤(1991—)，女，硕士研究生。E-mail: mayantong@sia.cn

郑荣(1963—)， 男， 研究员， 博士生导师。 E-mail: zhengr@sia.cn

TP273+.1

A

1000-1093(2017)06-1147-07

10.3969/j.issn.1000-1093.2017.06.014