基于多维关系复杂网络的装备重要度评估方法

陈春良， 昝翔， 张仕新， 曹艳华， 陈伟龙

(装甲兵工程学院 技术保障工程系， 北京 100072)

基于多维关系复杂网络的装备重要度评估方法

陈春良， 昝翔， 张仕新， 曹艳华， 陈伟龙

(装甲兵工程学院 技术保障工程系， 北京 100072)

针对现有装备重要度评估方法，考虑装备体系结构关系单一的问题，设计一种基于多维关系复杂网络的装备重要度评估方法。全面考虑装备之间的指挥控制关系、空间关系和协同关系，建立基于复杂网络的装备体系结构模型，在充分分析不同关系网络特征的基础上，选取合适的特征参数，构建节点重要度评估指标。综合考虑节点结构重要度和属性重要度，采用改进层次分析法进行节点重要度综合评估。通过一个具体算例，验证了该方法的合理性和有效性。

兵器科学与技术； 复杂网络； 装备重要度； 节点重要度评估； 改进层次分析法

0 引言

装甲机械化部队战时装备体系是由参与作战的各装备在作战空间内相互作用而构成的一个复杂系统。不同类型的装备在作战中发挥的作用不同，这使得它们在装备体系中的重要程度存在差异。装备重要程度既是装备对作战支持作用的定量化体现，也会对装备维修保障任务优先级分类产生重要影响。

装备重要度能够定量反映装备对于整个装备体系完整性的影响，而保持装备体系的完整是充分发挥装备作战效能的关键因素。复杂网络理论中的节点重要度评估方法目前主要用于对指挥信息网络中的关键节点进行识别[1]。随着体系作战思想的不断发展和装备体系理论的不断完善，将装备体系抽象为复杂网络，装备抽象为复杂网络中的节点，应用节点重要度评估方法进行装备重要度评估，成为装备重要度评估研究的发展趋势。张勇等[2]对应用节点重要度评估方法对装备重要度评估方法进行了改进，同时描述了装备重要度和失效后的修复状况。姜志鹏等[3]考虑了多种影响因素，建立了考虑多维约束的装备重要度评估模型。

根据具体问题合理选择参数是进行节点重要度评估的关键。复杂网络的基本参数包括介数[4]、节点权重[5]、节点贡献度[6]等。随着研究的深入，节点重要度评估方法也在不断改进，一方面人们将各种参数进行融合，提出节点凝聚度[7]等新的参数，一方面又提出了节点收缩法[8]、K-核分解法[9]等新方法。刘建国等[10]对复杂网络节点重要度评估方法和参数进行了总结与归纳。目前，节点重要度评估绝大部分针对无权无向网络，虽然出现了针对加权网络[11]和有向加权网络[12]的节点重要度评估方法的研究，但是不够深入，尚处于起步阶段。

通过基于复杂网络的装备重要度评估的研究现状和节点重要度评估方法的研究现状两个部分的分析，主要发现了以下3个问题：

1)以复杂网络为基础构建装备重要度模型时，只考虑了装备之间的指挥控制关系，忽略了装备之间的其他联系，应该综合考虑装备之间不同性质的关系，构建更加符合实际的装备体系结构模型；

2)大部分研究忽略了装备自身属性对重要度的影响，只考虑装备在体系结构中的重要度，应该综合考虑两方面的因素进行装备重要度评估；

3)没有根据不同性质复杂网络的特点选择合适的评估参数。

针对以上问题，本文提出基于复杂网络的装备重要度评估方法，充分分析装备之间的指挥控制关系、空间关系和协同关系，并针对不同关系网络的特点选取合适的评估参数，综合考虑节点结构重要度和属性重要度获得重要度评估值，应用改进层次分析法确定指标权重，并通过算例对该方法进行验证。

1 基于复杂网络的装备体系结构建模与网络特征分析

1.1 基于复杂网络的装备体系结构建模

复杂网络由节点及节点间的错综复杂关系共同组成[13]。复杂网络模型由点和边构成，模型中的点代表发挥功能的每一个个体，而边则表示个体的相互联系[14]。该模型可以用来描述真实世界个体之间复杂的相互关系，并为描述和分析这些复杂关系提供理论和方法支撑。

在装备体系中，装备之间的关系存在多样性，单一的关系不能完整地描述装备体系结构的特征，需要从指挥控制关系、空间关系和协同关系3个方面进行分析，建立基于复杂网络的装备体系结构模型。

1)V=(v1,v2,…,vn)是节点的集合，将装备视为装备体系中的一个节点。

2)指挥控制关系wc(i,j)表示从节点vi到节点vj的通信强度。wc(i,j)∈[0,1]，可通过对节点vi到节点vj的通信强度进行评估给出。当节点vi到节点vj无通信交流时，wc(i,j)=0；特别地，可认为wc(i,i)=0. 指挥控制关系结构由wc(i,j)组成的邻接矩阵Wc表示。

3)空间关系wr(i,j)反映节点vi与节点vj之间的距离，取值为距离的倒数。wr(i,j)∈[0,∞)，当节点vi与节点vj之间距离相对于其他节点之间的距离很远时，可认为wr(i,j)=0；当节点vi与节点vj之间距离相对于其他节点之间的距离很近时，可认为wr(i,j)=∞. 空间关系结构由wr(i,j)组成的邻接矩阵Wr表示。

4)协同关系ws(i,j)表示节点vi对节点vj的协同作用。ws(i,j)∈{0,1}，当ws(i,j)=0时，表示节点vi对节点vj有协同；当ws(i,j)=1时，表示节点vi对节点vj没有协同。协同关系结构由ws(i,j)组成的邻接矩阵Ws表示。

根据数学描述，可将装备体系结构模型表示为

G(V,Wc,Wr,Ws).

(1)

1.2 多维关系复杂网络特征分析

G(V,Wc,Wr,Ws)是反映多种关系特征的装备体系结构模型，可称为多维关系复杂网络模型，基本结构如图1所示，图1中w为节点间的边权重，表示部分关系网络中节点间关系的强度存在差异。

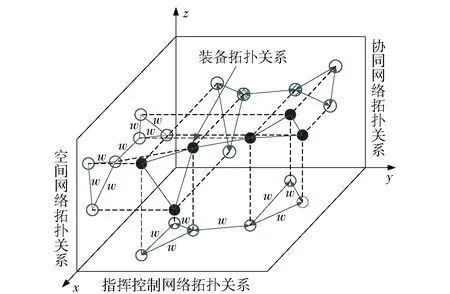
图1 装备体系结构模型Fig.1 Model of equipment architecture

1)由于指挥控制关系存在信息的上传和下达两个方向，并且通信的强度存在差异，因此指挥控制关系网络G(V,Wc)是一个有向加权网络。装备之间的信息交流存在多种方式且通信强度不同，导致装备之间的指挥控制关系强度可以发生变化。

2)空间关系反映的是装备之间的距离关系。在不同的作战队形中，装备所处的位置和发挥的作用存在差异。因此，空间关系网络G(V,Wr)是一个无向加权网络。

3)协同关系表示的是装备之间相互支援的关系，装备的功能差异导致相互之间的支援作用不同，并且支援关系是有向的。因此，协同关系网络G(V,Ws)是一个有向无权网络。

1.3 复杂网络特征参数分析

装备体系结构网络模型包括有向加权网络、无向加权网络和有向无权网络3种，下面对部分特征参数[15]进行分析。

1.3.1 节点的度k(i)

节点vi的度k(i)为与该节点连接边的个数，反映无向无权网络节点的重要程度。

1.3.2 节点强度S(i)

节点强度S(i)为所有直接指向节点vi的边权重w(i,j)的和，表征节点在无向加权网络中的影响力。

1.3.3 节点间路径长度d(i,j)

节点间路径长度d(i,j)指的是从节点vi到节点vj的最短路径。无向无权网络中，d(i,j)的取值为节点之间最短路径的边数。在有向加权网络中，d(i,j)可以按照如下的方式计算：若从节点vi到节点vj的最短路径要经过k个中间节点，则d(i,j)可以表示为

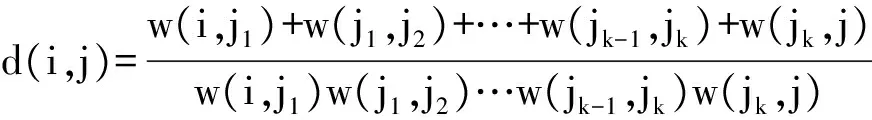
(2)

式中：w(i,j1)、w(j1,j2)、…、w(jk-1,jk)、w(jk,j)为节点vi到节点vj最短路径需要经过边的权重值。

1.3.4 节点接近度C(i)

节点接近度C(i)是所有可以到达节点vi的节点路径长度和的倒数，可以反映节点的位置信息。

1.3.5 网络效率ε

节点间的网络效率ε与路径长度呈反比[16]。

2 节点重要度评估方法

2.1 评估指标体系构建

综合考虑节点的结构重要度和属性重要度，建立如图2所示的节点重要度评估指标体系。

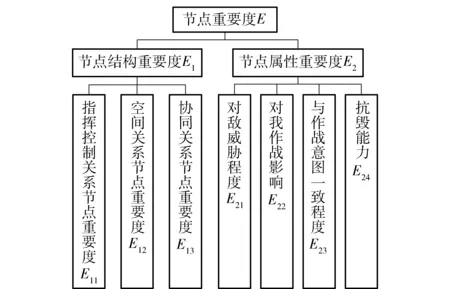
图2 节点重要度评估指标体系Fig.2 Evaluation index system for node importance

明确了评估指标体系后，评估值计算和指标权重确定成为进行节点重要度评估两个重要组成部分。在该指标体系中，节点的结构重要度需要基于装备体系结构模型，选取合适的参数进行定量计算。节点属性重要度值则可以通过定性评估直接获得。

2.2 节点重要度评估值计算

2.2.1 节点结构重要度评估值

节点结构重要度以装备体系结构模型为基础，根据不同关系网络的特点，综合考虑节点在局部结构和全局结构两个方面的重要度，选择合适的参数计算指挥控制关系网络、空间关系网络和协同关系网络的结构重要度E11、E12和E13.

2.2.1.1E11的计算

在指挥控制关系网络中，节点局部结构重要度用节点重要度贡献参数表示，节点全局结构重要度用节点对信息传输的影响程度表示。

1)E11的局部结构重要度参数

复杂网络中节点之间最主要的影响关系存在于相邻节点之间，构成一个节点重要度贡献矩阵[17]。指挥控制关系网络为有向加权网络，节点重要度贡献矩阵以节点强度S(i)为基础构建，其表达式为

HIC=

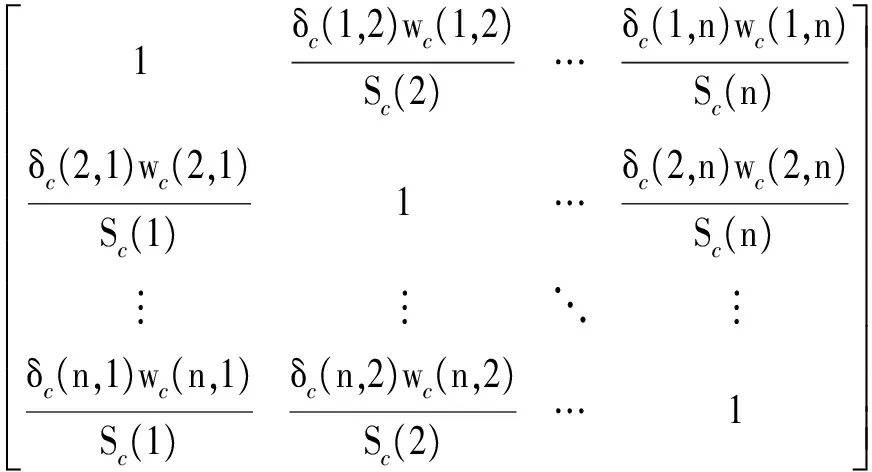
(3)

式中：n为网络中的节点总数；wc(i,j)为指挥控制关系网络中从节点vi到节点vj的边权重值；Sc(i)为节点vi在指挥控制关系网络中的节点强度，其表达式为

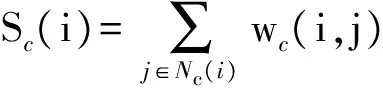
(4)

其中，Nc(i)表示指挥控制关系网络中直接指向节点vi的节点集合。

δc(i,j)为指挥控制关系网络中的贡献参数，取值方式为

(5)

2)E11的全局结构重要度参数

指挥控制关系网络中的网络效率表达式为

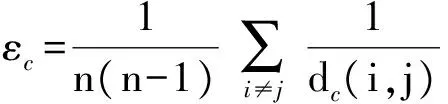
(6)

式中：dc(i,j)为指挥控制关系网络中从节点vi到节

点vj的路径长度。

若去除节点g后，网络效率变为

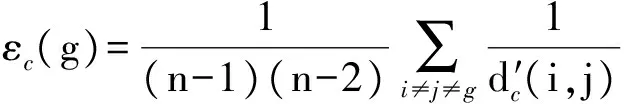
(7)

式中：d′c(i,j)为去除节点g后，从节点vi到节点vj的最短路径。

设去除节点g后，从节点vi到节点vj的最短路径要经过k′c个中间节点，则d′c(i,j)可以表示为

d′c(i,j)=

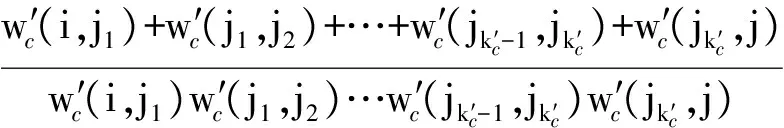
(8)

式中：w′c(i,j1)、w′c(j1,j2)、…、w′c(jk′-1,jk′)、w′c(j,jk′)表示去除节点g后，节点vi到节点vj的最短路径需要经过的边权重值。

网络效率的变化率为

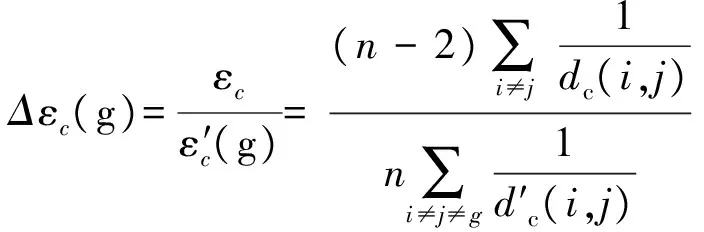
(9)

在计算网络效率变化率时，为了避免出现去除某一节点后网络效率变大的情况，将节点g对信息传输的影响度表示为

(10)

3)E11的计算式

将局部结构重要度参数与全局结构重要度参数融合，得指挥控制关系网络节点重要度评估矩阵为

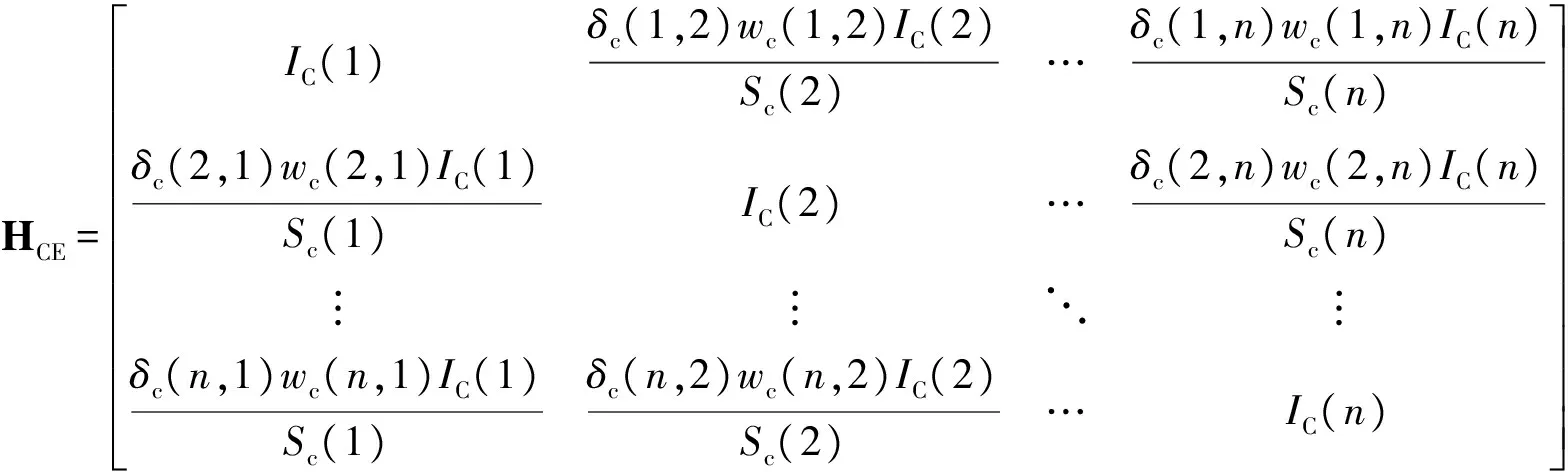
(11)

通过(11)式，可得节点vi的E11的计算式为

(12)

2.2.1.2E12的计算

在空间关系网络中，节点局部重要度用节点强度表示，节点全局重要度用节点接近度表示。

1)E12的局部结构重要度参数

空间关系网络节点vi的强度表达式为

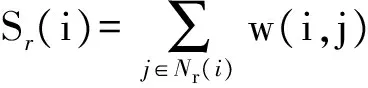
(13)

式中：Nr(i)表示在空间关系网络中与节点vi的直接连接的节点集合。

2)E12的全局结构重要度参数

空间关系网络节点接近度的表达式为

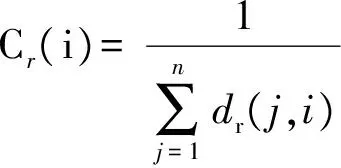
(14)

式中：dr(j,i)为空间关系中从节点vj到节点vi的路径长度。

3)E12的计算式

将局部结构重要度参数与全局结构重要度参数融合，可得vi的E12的计算式为

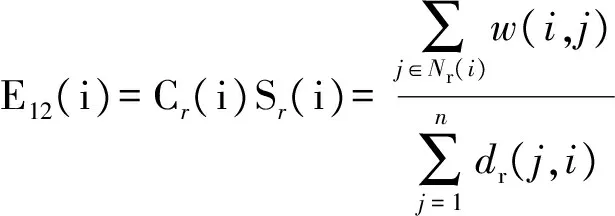
(15)

2.2.1.3E13的计算

在协同关系网络中，节点局部重要度用重要度贡献参数表示，节点全局重要度用节点接近度表示。

1)E13的局部结构重要度参数

协同关系网络的局部重要度通过节点对相邻节点的贡献程度表示，其表达式为

(16)

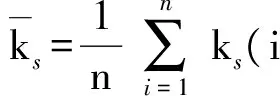
(17)

δs(i,j)为协同关系网络中的贡献参数，取值方式为

(18)

2)E13的全局结构重要度参数

协同关系网络节点接近度的表达式为

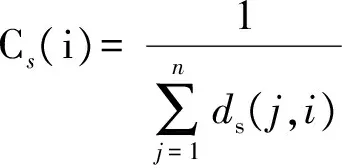
(19)

式中：ds(j,i)为协同关系中从节点vj到节点vi的路径长度。

3)E13的计算式

将局部结构重要度参数与全局结构重要度参数融合，得协同关系网络节点重要度评估矩阵为

(20)

通过(20)式，可得节点vi的E13计算式为

(21)

通过(12)式、(15)式、(21)式可以计算出节点结构重要度的评估值。

2.2.2 节点属性重要度评估值

选择取若干名相关领域的专家，通过专家打分法对E21、E22、E23和E24进行定性评估，并将各专家打分的平均值作为节点属性重要度的评估值。

2.3 基于改进层次分析法的指标权重确定

根据评估指标体系层次性特点可以采用改进层次分析法(IAHP)求解指标权重，与标准的层次分析法相比，IAHP用三标度法建立判断矩阵，同时可以省略一次性检验的环节，具有更强的适应性[18]。利用IAHP确定指标权重的具体流程如下。

2.3.1 判断矩阵

对同一层次上的指标进行两两比较分析，采用三标度法进行定量化，具体含义见表1.

表1 三标度法定义Tab.1 Definition of three-standard degree method

由此可得判断矩阵A的表达式为

(22)

式中：i、j=1，2，…，u.

2.3.2 传递矩阵

以A为基础，构建传递矩阵Z=(zij)u×u，其中

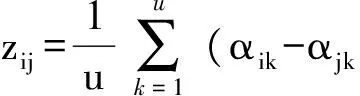
(23)

2.3.3 拟优化传递矩阵

构建A的拟优化传递矩阵B=(bij)u×u，由于B=eZ为一致矩阵，故满足一致性检验的要求，并且有

bij=exp (zij).

(24)

2.3.4 指标权重

计算B的最大特征值λmax的特征向量ξ，归一化后，可得所求的指标权重。令一级指标E1和E2的权重分别为θ1和θ2，则二级指标的权重集合为

Θ={θ11,θ12,θ13,θ21,θ22,θ23,θ24}.

(25)

2.4 评估结果确定

在获得了节点重要度评估值和确定了各评估指标的权重后，可得节点重要度评估的计算式为

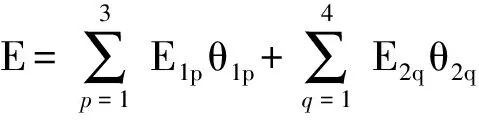
(26)

E为节点重要度最终评估结果，即为该节点所对应装备重要度评估结果。

3 算例分析

3.1 算例构建

3.1.1 作战背景

为了验证所述评估方法，构建以下算例：某装甲机械化部队执行某机动进攻作战任务，在该次进攻中需要部署4个地面突击群，采用机动合围的作战方法，两个突击群从正面分成两个梯队进行突击，另外两个突击群分别从两翼对敌实施进攻，目的是夺取关键要点，驱逐或消灭敌有生力量。基本作战部署示意图如图3所示。

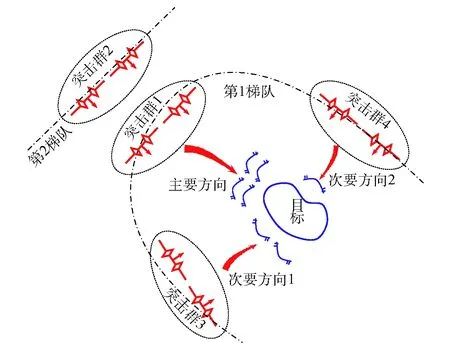
图3 某机动进攻作战部署示意图Fig.3 Deployment of flexible attack operation

3.1.2 装备构成及拓扑结构分析

根据装甲机械化部队的编制、装备构成以及发展趋势，每个突击群由1个作战营组成，每个作战营配属3个作战连和1个营部连，每连配有1台指挥装备和9台作战装备。突击群内部连、排均采用倒三角的基本作战队形，并做出如下说明：

1)各营的营部连为1连，前突的两个连分别为2连和3连，靠后的连为4连；

2)各连前突的两个排分别为2排和3排，靠后的为1排。

装备基本拓扑结构及隶属关系如图4所示。

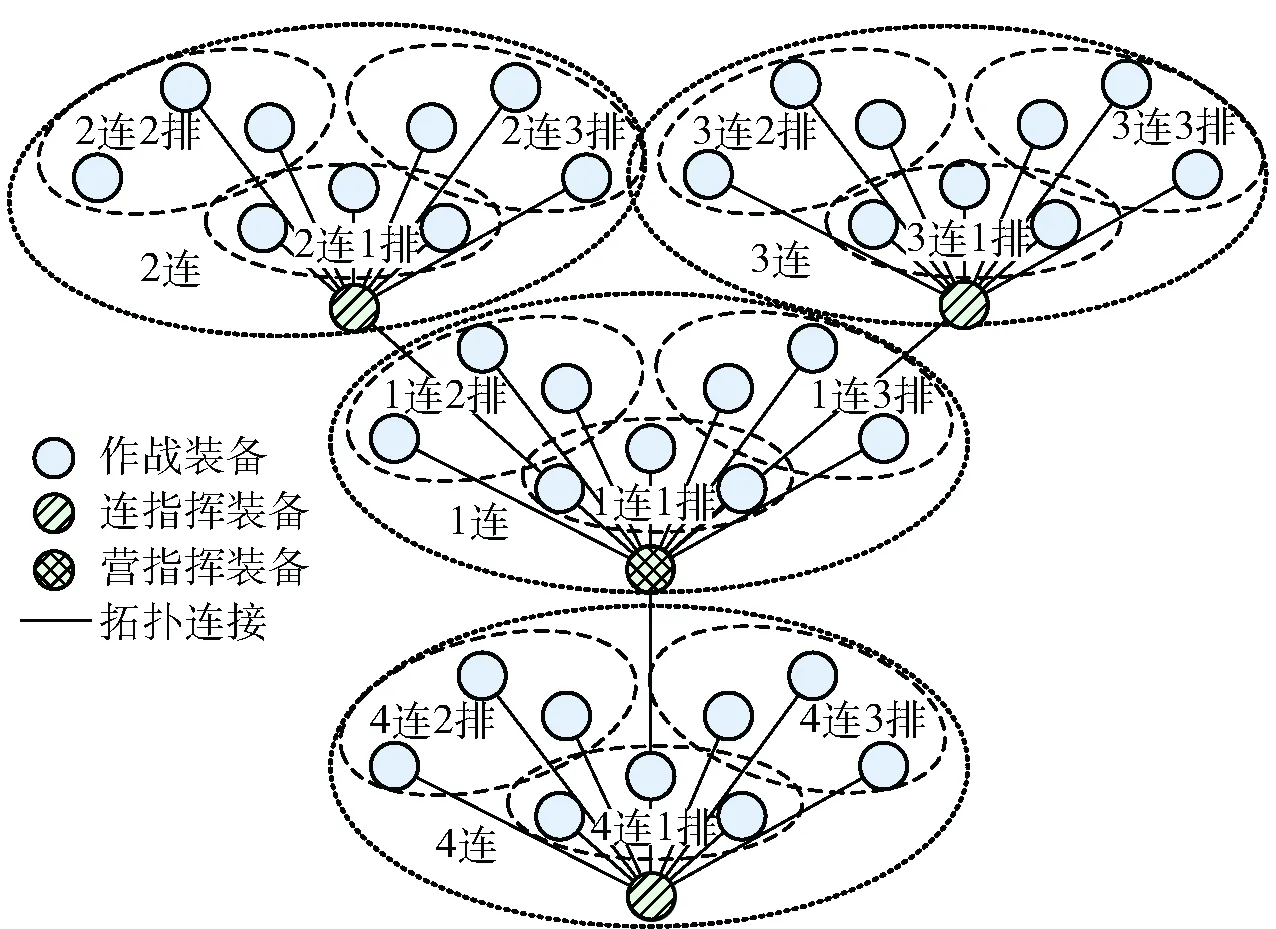
图4 装备基本拓扑结构及隶属关系Fig.4 Basic topological structure and subordination relationship of equipment

3.1.3 装备体系结构分析

对装备进行编号，在突击集群内部1连的装备编为v1-1～v1-10，2、3、4连的装备编为v2-1～v2-10、v3-1～v3-10、v4-1～v4-10，设定每个连的1号装备为指挥装备，即v1-1表示营指挥装备，v2-1、v3-1、v4-1表示连指挥装备，其余均为作战装备。每个连内部，1排的装备编号为v2-2～v2-4、v3-2～v3-4、v4-2～v4-4，其余为2排和3排的装备。突击集群1～突击集群4的装备加上前缀T1～T4进行区分。

信息化作战的空间大大增加，各突击群会在指挥信息系统的统一指挥下，相对独立的遂行作战任务，可以认为装备体系内部的指挥控制关系、空间关系和协同关系只存于与每个突击群内部。由于每个突击群的装备组成和内部关系均相同，只需以一个突击群内部的装备体系结构为例进行分析。

3.1.3.1 指挥控制关系网络

指挥装备损坏会导致装备之间通信强度发生变化，假设权重变化为阶跃函数，可设定受影响的边权重下降为原来的70%. 为了更加简洁地表达装备体系结构，将发挥同种作用的节点进行合并，可得指挥控制网络简化拓扑结构如图5所示。

图5 指挥控制网络简化拓扑结构Fig.5 Simplified topological structure of command and control relationship networks

3.1.3.2 空间关系网络

根据装甲部队作战的相关原则和信息化作战的发展趋势，担负进攻作战营的进攻正面约为2 km，进攻纵深约为2 km. 为了更加简洁地表达装备体系结构，将部分空间距离相同的节点进行合并，可得空间网络简化拓扑结构如图6所示。

图6 空间网络简化拓扑结构Fig.6 Simplified topological structure of spatial relationship networks

图6中所示的边权重值是装备之间的距离以百米为单位的倒数值。根据装甲部队进攻作战基本队形，同一个排的3台装备之间距离较近，可取边权重为∞，同一排的装备与外部装备的空间关系完全相同，可视为同一节点；由于连与连之间装备的距离远远大于连内部之间装备的距离，可取指挥装备之间的距离作为全连所有装备与另一连所有装备之间的距离，即连与连之间任意两台装备之间的边权重相等。

3.1.3.3 协同关系网络

装备之间的协同关系主要存在于同一连的装备之间，连与连之间的协同关系可以通过指挥装备之间的协同关系反映，即不属于同一连的作战装备之间没有协同关系。为了更加简洁地表达装备体系结构，将相同属性节点进行合并，可得协同网络简化拓扑结构如图7所示。

3.2 装备重要度评估

通过IAHP获得各评估指标的权重如表2所示。

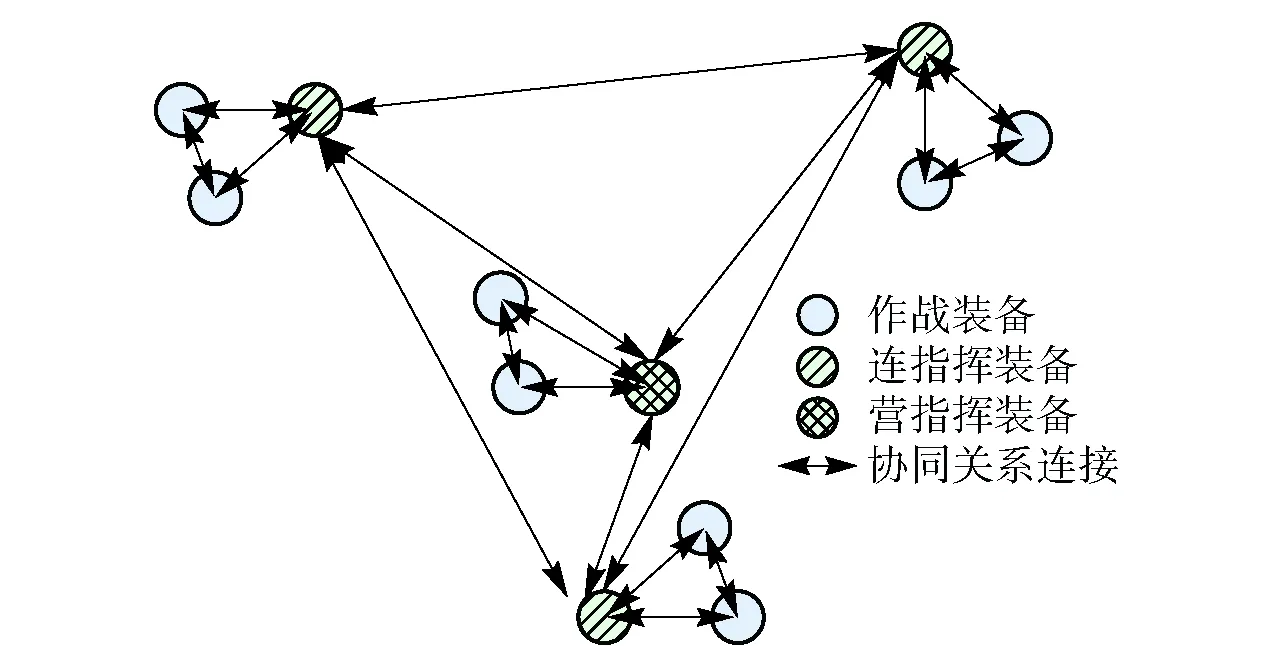
图7 协同网络简化拓扑结构Fig.7 Simplified topological structure of cooperative relationship networks

项目权重θ11θ12θ13θ21θ22θ23θ24θ1θ2本层056015029028046017010073027合成041011021007012005003073027

按照(16)式、(19)式、(25)式，计算节点的结构重要度，定性评估节点属性重要度，根据所得的指标权重，最终可得装备重要评估结果。由于算例中装备数量众多(160台装备)，而篇幅有限，故选取部分有代表性的装备重要度评估结果在表3中展示。

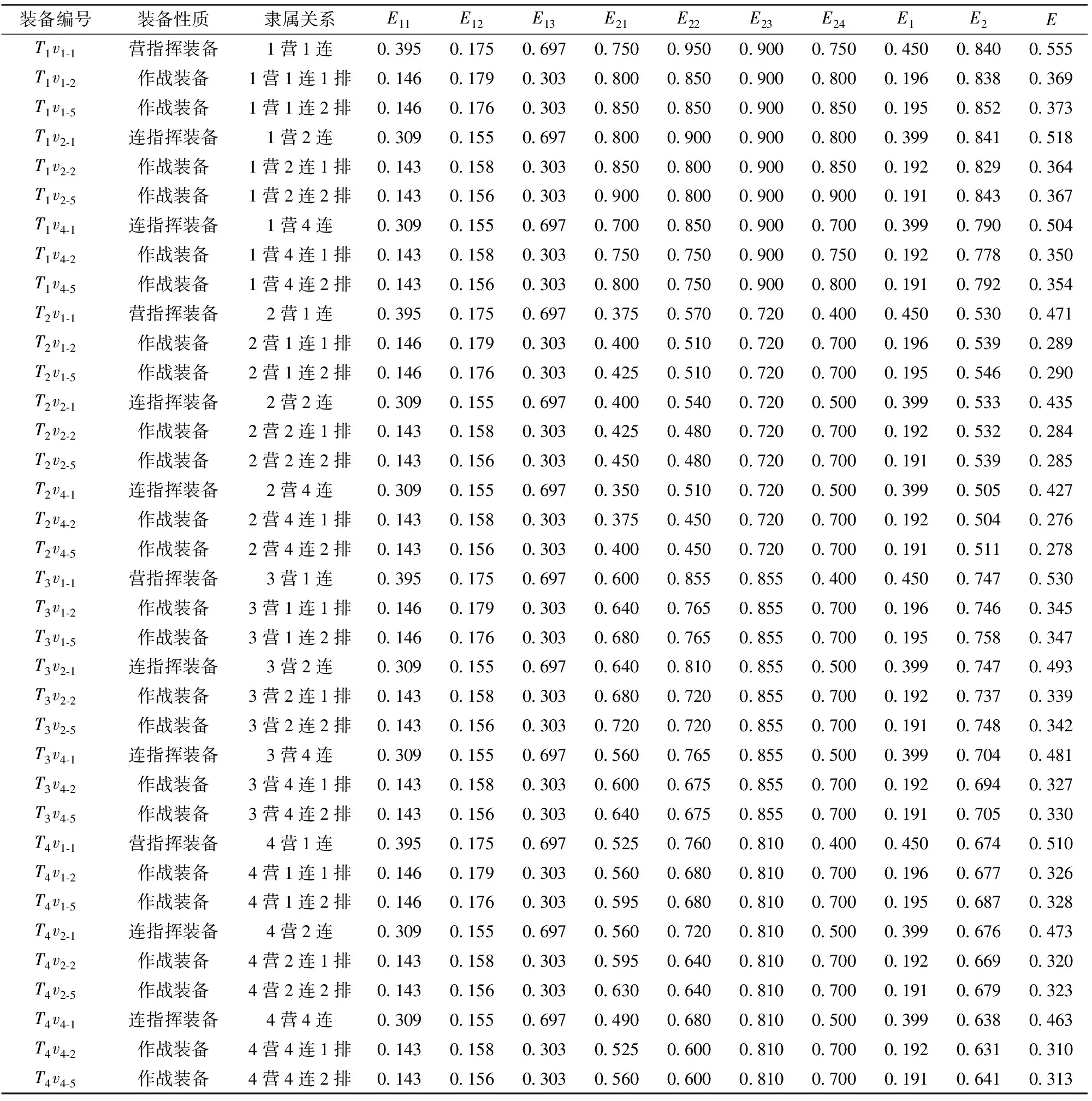
表3 装备重要度评估结果(节选)Tab.3 Evaluated results of equipment important degree

3.3 评估结果分析

1)在同一突击群中，指挥装备的重要度大于作战装备，营指挥装备的重要度大于连指挥装备的重要度。例如，装备T1v1-1的重要度大于装备T1v2-1，装备T1v1-1的重要度大于装备T1v1-2. 结果符合装备重要度比较的相关原则，表明应用该方法进行装备重要度的评估具有合理性，评估结果可信。

2)不同性质的关系均会对装备结构重要度产生影响。例如，装备T1v1-2和装备T1v1-5为同一个营同一个连的作战装备，指挥控制关系和协同关系重要度也相同，但是由于在连内的位置不同，使得空间关系存在差异，导致它们在装备体系中的结构重要度出现差异。

3)装备重要度比较的相关原则具有一定适用范围。根据重要度评估结果，可以发现2营的营指挥装备(T2v1-1)和重要度低于1营的连指挥装备(T1v2-1和T1v4-1)，说明营指挥装备重要度大于连指挥装备这一原则只在同一作战营中有效。

4 结论

1)在装备体系中，装备的相互关系和装备本身的属性均会对装备重要度产生影响，即在基于复杂网络进行节点重要度评估时，节点的重要度是由节点的结构重要度和属性重要度共同决定的。

2)在装备体系中，装备与其他装备的指挥关系、空间关系和协同关系均会对其结构重要度产生影响。本文所提出的方法能够分析装备体系中不同性质关系之间的差异，解决了单一关系网络不能解决的问题。

3)根据作战的基本规律和装备保障的原则，装备重要度比较的相关原则可以用于比较相同条件下不同种类的装备重要度，对于处于不同作战位置、相互关系不同的不同种类装备并不适用。本方法可以解决一般的装备重要度评估方法无法解决的问题，即在不同条件下不同种类装备重要度的比较问题。

体系作战是未来作战的主要发展趋势，在装备体系中，装备重要度不仅与装备本身的属性有关，而且受到装备在体系中相互关系的影响。由于装备之间的相互关系存在多样性，装备体系具有不同性质的体系结构。本文所述方法可以将装备对作战的支持作用定量化，更加有力地说明不同装备对保证装备体系完整性和作战任务的完成所发挥的作用，同时也为装备维修保障任务优先级分类打下了坚实的基础，值得推广应用。

References)

[1] 王欣,姚佩阳,周翔翔,等.指挥信息系统网络节点重要度评估方法[J].北京邮电大学学报,2011,34(4):38-42. WANG Xin, YAO Pei-yang, ZHOU Xiang-xiang, et al. A new evaluation on node importance in command information system[J]. Journal of Beijing University of Posts and Telecommunications, 2011,34(4):38-42.(in Chinese)

[2] 张勇,杨宏伟,白勇.基于复杂网络的武器装备重要度评估方法[J].装甲兵工程学院学报,2012,26(1):5-9. ZHANG Yong, YANG Hong-wei, BAI Yong. Evaluation method for weapons important degree based on complex networks[J]. Journal of Academy of Armored Force Engineering, 2012,26(1):5-9.(in Chinese)

[3] 姜志鹏,张多林,王乐,等.多维约束下指挥网络节点重要度的评估方法[J].解放军理工大学学报：自然科学版,2015,16(3):294-298. JIANG Zhi-peng, ZHANG Duo-lin, WANG Le, et al. Evaluation method for node importance of command network with multiple constraints[J]. Journal of PLA University of Science and Technology:Natural Science Edition, 2015,16(3):294-298.(in Chinese)

[4] Zhu D H, Wang D D, Hassan S U, et al. Small-world phenomenon of keywords network based on complex network[J]. Scientometrics, 2013,97(2):435-442.

[5] Mayo M, Abdelzaher A, Ghosh P. Long-range degree correlations in complex networks[J]. Computational Social Networks, 2015,2(1):1-13.

[6] Liu J, Xiong Q Y, Shi W R, et al. Evaluating the importance of nodes in complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2016,452(15):209-219.

[7] Tang L K, Lu J A, Wu X Q, et al. Impact of node dynamics parameters on topology identification of complex dynamical networks[J]. Nonlinear Dynamics, 2013,73(1):1081-1097.

[8] 谭跃进, 吴俊, 邓宏钟. 复杂网络中节点重要度评估的节点收缩方法[J]. 系统工程理论与实践, 2006, 26(11):79-83,102. TAN Yue-jin, WU Jun, DENG Hong-zhong. Evaluation method for node importance based on node contraction in complex networks[J]. Systems Engineering-Theory and Practice, 2006,26(11):79-83,102.(in Chinese)

[9] 任卓明,刘建国,邵凤,等.复杂网络中最小K-核节点的传播能力分析[J].物理学报,2013,62(10):1-6. REN Zhuo-ming, LIU Jian-guo, SHAO Feng, et al. Evaluation analysis of the spreading influence of the nodes with minimum K-shell value in complex networks[J]. Acta Physica Sinica, 2013,62(10):1-6.(in Chinese)

[10] 刘建国,任卓明,郭强,等.复杂网络中节点重要性排序的研究进展[J].物理学报,2013,62(17):1-9. LIU Jian-guo, REN Zhuo-ming, GUO Qiang, et al. Node importance ranking of complex networks[J]. Acta Physica Sinica, 2013,62(17): 1-9.(in Chinese)

[11] 谢琼瑶,邓长虹,赵红生,等.基于有权网络模型的电力网节点重要度评估[J].电力系统自动化,2009,33(4):21-24. XIE Qiong-yao, DENG Chang-hong, ZHAO Hong-sheng, et al. Evaluation method for node importance of power grid based on the weighted network model[J]. Automation of Electric Power Systems, 2009,33(4):21-24.(in Chinese)

[12] 张琨,李配配,朱保平,等.基于PageRank的有向加权复杂网络节点重要性评估方法[J].南京航空航天大学学报,2013,45(3):429-434. ZHANG Kun, LI Pei-pei, ZHU Bao-ping, et al. Evaluation method for node importance in directed-weighted complex networks based on PageRank[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2013,45(3):429-434.(in Chinese)

[13] 孙玺菁,司守奎.复杂网络算法与应用[M].北京:国防工业出版社,2015. SUN Xi-jing, SI Shuo-kui. Complex network algorithm and applications[M]. Beijing: National Defense Industry Press, 2015.(in Chinese)

[14] Shanker O. Complex network dimension and path counts[J]. Theoretical Computer Science, 2010,411(26/27/28):2454-2458.

[15] 魏代俊.复杂网络分形性质及应用研究[D].重庆:西南大学,2014. WEI Dai-jun. Fractal property of complex networks and its application[D]. Chongqing: Southwest University, 2014. (in Chinese)

[16] 罗小明,何榕,朱延雷.武器装备体系结构贡献度评估[J].装甲兵工程学院学报,2016,30(8):1-6,23. LUO Xiao-ming, HE Rong, ZHU Yan-lei. Research on evaluation of contribution to weapon equipment system architecture[J]. Journal of Academy of Armored Force Engineering, 2016,30(8):1-6,23.(in Chinese)

[17] 周漩,张凤鸣,李克武,等.利用重要度评估矩阵确定复杂网络关键节点[J].物理学报,2012,61(5): 1-7. ZHOU Xuan, ZHANG Feng-ming, LI Ke-wu, et al. Finding vital node by node importance evaluation matrix in complex networks[J]. Acta Physica Sinica, 2012,61(5):1-7.(in Chinese)

[18] 彭绍雄,王海涛,邹强.潜空导弹武器系统作战效能评估模型[J].系统工程理论与实践,2015,35(1):267-272. PENG Shao-xiong, WANG Hai-tao, ZOU Qiang. Combat effectiveness evaluation model of submarine-to-air missile weapon system[J]. Systems Engineering Theory and Practice, 2015,35(1):267-272.(in Chinese)

Evaluation Method for Equipment Important Degree Based onMultidimensional Relationship Complex Networks

CHEN Chun-liang, ZAN Xiang, ZHANG Shi-xin, CAO Yan-hua, CHEN Wei-long

(Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing 100072，China)

A new equipment important degree evaluation method based on multidimensional complex networks is designed in consideration of equipment architecture. Command and control relationship, spatial relationship and cooperative relationship are considered and introduced into an equipment architecture model based on complex networks. Appropriate parameters are chosen to establish the node importance evaluation index by analyzing the features of different relationship networks. An improved analytic hierarchy process is applied in node architecture importance comprehensive evaluation by considering both node architecture importance and node attribute importance. An example is used to validate the retionality and effectuality of the proposed method.

ordnance science and technology; complex network; equipment important degree; node importance evaluation; improved analytic hierarchy process

2016-11-04

军队科研计划项目(2015WG57)

昝翔(1989—)，男，博士研究生。E-mail：994401550@qq.com

陈春良(1963—)，男，教授，博士生导师。E-mail：chenchunliang@163.com

E92

A

1000-1093(2017)06-1168-10

10.3969/j.issn.1000-1093.2017.06.017