多通道瞬态信号自适应变频算法
2017-07-10王啸韩太林张永立刘轩王义君宫玉琳
王啸, 韩太林, 张永立, 刘轩, 王义君, 宫玉琳
(长春理工大学 电子信息工程学院, 吉林 长春 130022)
多通道瞬态信号自适应变频算法
王啸, 韩太林, 张永立, 刘轩, 王义君, 宫玉琳
(长春理工大学 电子信息工程学院, 吉林 长春 130022)
为了解决在多通道瞬态信号测试领域,传统测试系统长时间高采样率测试产生的冗余数据对系统存储和传输带来的压力,提出了一种自适应变频算法。该算法采用与传统测试相同的采样率获取原始数据并以时间分段,依据每段信号的频域特征确定瞬态信号发生时刻和持续时间,对非瞬态信号进行二次采样,达到在完整保留瞬态信息的前提下减少冗余数据的目的。在实际爆炸冲击波场测试中进行验证,经过算法处理后数据压缩比大于33,同时保证瞬态信号持续期间数据完整,非瞬态信号持续期间最大误差小于0.5FS. 试验结果表明,该算法可有效减少瞬态测试过程中的冗余数据。
信息处理技术; 瞬态测试; 自适应变频; 数据预处理
0 引言
瞬态信号是指在背景噪声下突发,时域持续时间短,有明显的开端和结束节点的信号[1]。近几年来,瞬态信号的检测已逐渐发展成为一个重要的问题,例如在水声、语音、雷达、地震、生物医学和武器测试等许多领域瞬态信号的定量分析起到越来越重要的作用[2-3]。
在火箭发射、汽车碰撞和武器测试时传统测试系统通常采用100 kSa/s~10 MSa/s不等的采样率[4-5],同时由于信号的突发特征,为保证对随机产生的瞬态信号进行捕获并完整采集,要求采集时间数倍于瞬态信号持续时间,大大增加了采集系统实时存储和传输的压力,在场测试时采用多通道采集方式,单次采集获取数据为1~10 GB[6-7],故在瞬态信号测试时会产生大量冗余数据。
为解决传统瞬态测试系统中存在的冗余数据问题,电子测试技术国家重点实验室于2014年提出了负延迟和变频采样技术[8]。结合负延迟技术,在瞬态信号到达后,系统采用高采样率采集数据,在等待瞬态信号阶段采用低采样率,从而减少测试过程获取的冗余数据。但由于瞬态信号上升沿持续时间短,触发电平前的短暂时间里包含重要被测信息,而由于触发前的低采样率导致被测信息永久丢失,不可完整重建触发前信号波形。
陈昌鑫等[9]于2015年在冲击加速度存储测试中,在已知被测信号变化规律的测试场合提出变频采样策略。系统以高采样率采集数据,同时根据已知的被测信号特征,通过定时的方式改变对测得数据的抽取速率。从而可以达到在减少冗余数据的同时,完整重建被测信号。但由于大部分瞬态信号均有不可预知其发生和持续时间的特征,故此方法有一定局限性。
本文以火炮膛口冲击波为研究目标,提出自适应变频算法,解决了传统测试设备存在的产生大量冗余数据的问题[10]。文中涉及的多通道瞬态信号测试系统采用64通道进行采集,每通道采样率最高为2 MSa/s,单次测试持续时间根据被测目标不同约为10~30 s. 系统每秒产生512 MB数据,单次试验将产生5.12~15.36 GB数据(为方便阅读文中M,G单位统一为十进制),其中包含大量冗余数据。采集系统的数据产生速率已经远远超过1 000 Mbit/s以太网的理论传输速率[11],故为实现远程实时监控,需对采集数据进行预处理。
1 冲击波特性分析

图1 理想冲击波信号Fig.1 Ideal shock wave signal
其中系统的正压作用时间为测试主要性能指标,Sadovskiy提出了正压作用时间公式[12]为

(1)
式中:B为待定参数,通常取1~1.5;R是测试点到冲击波信号产生位置距离(m);w为药量(kg).
根据(1)式并结合系统测试范围,本测试系统所测信号的正作用时间范围为0.1~20 ms,占单次测试10~30 s持续时间的比例小于1%.
针对爆炸测量系统的上升时间性能,Patrick等提供了一个准则[13],如果τ是上升时间,有一个-3 dB的带宽f-3 dB.
τf-3 dB=0.35~0.45.
(2)
在该测试系统中,所测冲击波信号的频率范围为0.5~100 kHz. 因此上升时间在3 μs~1 ms之间。故测试系统采用2 MSa/s采样率进行采样,可确保采集到上升沿的准确位置。
针对瞬态信号的不可预测性、幅度和频率突变性等特征,提出自适应变频算法。
2 自适应变频算法
自适应变频算法流程图如图2所示,假设瞬态信号x(t)的最高频率为fH. 系统以采样率f0≥2fH进行采样,得到数据序列为x(n);对数据进行分段,有m(n)=x(n)Q(n),其中Q(n)为N长连续脉冲序列,N为分段后每段数据长度,有

(3)
式中:N′为每段数据起始点。

图2 算法整体流程图Fig.2 Overall flow chart of algorithm
对分段后数据m(n)进行离散傅里叶变换(DFT),得到

(4)
通过对X(k)进行判断,确定每段数据最高主频fiH(fiH≤fH),再依据奈奎斯特采样定理确定二次抽样率fi0(2fiH≤fi0≤f0),保证有效数据可完整重建,同时产生尽可能少的冗余数据。
单路瞬态信号采样T秒,可计算得传统测试总采样数为
Fc=f0×T.
(5)
对x(n)进行n段分段,每段时间为Ti,依据每段数据的频域特征确定是否对数据进行二次抽样,每段抽样比例为Mi(第i段抽样比例Mi≥1)倍。本算法测试总采样数为
(6)

η=Fc/Fa.
(7)
数据压缩比可作为对不同数据处理算法效果优劣的一条评价标准,其结果主要由Mi的取值决定。
2.1 门限条件确定

故可以根据频域门限得出分段后每段抽样比例条件公式:
(8)
为了使抽取后数据满足奈奎斯特采样定理,需满足
(9)
式中:fiH为第i段最高主频,即满足(8)式条件的最高频率。
由此可知,通过在频域内设置门限,可确定瞬态信号发生位置和持续时间,同时采用符合奈奎斯特采样定理的压缩操作,保证瞬态信息不丢失,为之后通过不同抽取方式进行数据压缩和数据恢复提供了保障。
2.2 二次采样方法
通过门限确定的常态数据段,系统对其进行二次抽样处理,以达到压缩冗余数据的目的。常用二次采样方法有等间隔采样和分段平均采样法。
2.2.1 等间隔采样
对原数据x(n)进行抽样比例为M的等间隔抽取,当M≠1时,抽取结果yD(n)等效于以采样率f0/M对x(t)采样得到数据,则有
yD(n)=x(Mn).
(10)
对抽样后数据yD(n)进行傅里叶变换可得

(11)
式中:YD(ejω)为yD(n)傅里叶变换;ω为归一化后数字频率。设原数据x(n)的数字频率为ω1,可知:
ω=ΩT2=ΩMT1=Mω1,
(12)


图3 等间隔采样算法流程Fig.3 Flow chart of equal-interval sampling algorithm
2.2.2 分段平均抽样
在被抽取数据段,为了减小奇异数据点引入的误差。可采用分段取平均的抽取方式,即对被抽取数据段,按照抽样间隔计算每个间隔内数据平均值。得到抽取后数据序列为

(13)
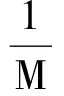
综上所述,算法可以对非瞬态数据段进行两种方式的自适应变频数据处理,实现压缩冗余数据的目的。下面针对两种数据重建模型对数据进行重建,恢复均匀采样结果。
2.3 数据重建方法
通过上述两种抽样方法,得到的处理后数据。由于各段抽样频率不同,数据序列呈现为非均匀采样,为了恢复原均匀采样结果,通常有线性插值和3次样条插值两种恢复方式。下面对不同重建方式进行分析。
2.3.1 线性插值
在每段数据均通过等间隔采样时,可依据每段抽样比例Mi对抽取后数据进行同比例插值重建数据。当Mi=1时,原数据未经过处理,则x′(n)=x(n);当Mi≠1时,针对不含有瞬态信息的分段数据可采用线性插值对数据进行重建,具体插值公式为

(14)
式中:x′(n)为重建后数据;x(i)为抽取后序列第i个数据点;需要符合iMi≤n≤(i+1)Mi,重建i与i+1之间数据。
2.3.2 3次样条插值
为了保证重建后数据保持平滑,在某些对重建波形要求较高的场合可采用比线性插值更复杂的3次样条插值。其三转角方程为

(15)
式中:mi=S′(xi);hi=xi+1-xi;通过自然边界条件S″(x0)=S″(xn)=0可确定S(x)表达式。从而完成对每段数据的重建。
采用不同的重建方式得到的重建数据长度和采样率均与抽取前数据相同,可完整反映原测试采集结果。
3 算法的实验与应用
为了验证上述算法的有效性,采取项目实际测试中测得的爆炸冲击波数据进行算法处理。计算算法压缩比,比较压缩数据重建后与原始数据最大差值以及压缩后数据波形变化程度等数据信息。
3.1 单次冲击数据处理
本次测试采用48个通道进行测试,单通道采样率为1 MSa/s,采集时间为5 s,其中预触发时长为2 s,每个采样点数据为4 B单精度浮点型格式存储。可计算测试共产生数据为
1 MSa/s×5 s×4 B×48=960 MB.
(16)
图4(a)为单通道瞬态信号原始波形,测试时间为5 s,设有预触发时长为2 s,可知瞬态信号发生在2 s位置。将原5 s数据沿x轴方向展开为50 ms得到图4(b)所示波形,可知瞬态信号持续时间约为20 ms,但由于数据通过传统固定采样率设备进行采集,全部数据均采用1 MSa/s速率进行采集,即其中4.98 s数据为严重过采样得到,可通过预处理算法进行压缩。

图4 瞬态信号原始波形Fig.4 Original waveform of transient signal

图5为全部5 s数据经过算法处理后波形,由图5可知,其中瞬态信号部分波形(两竖线之间)相比图4(a)原始数据中所占全部数据比例明显提升。同时,总数据量减少为156 100 B,约为156 kB,数据压缩比为128.
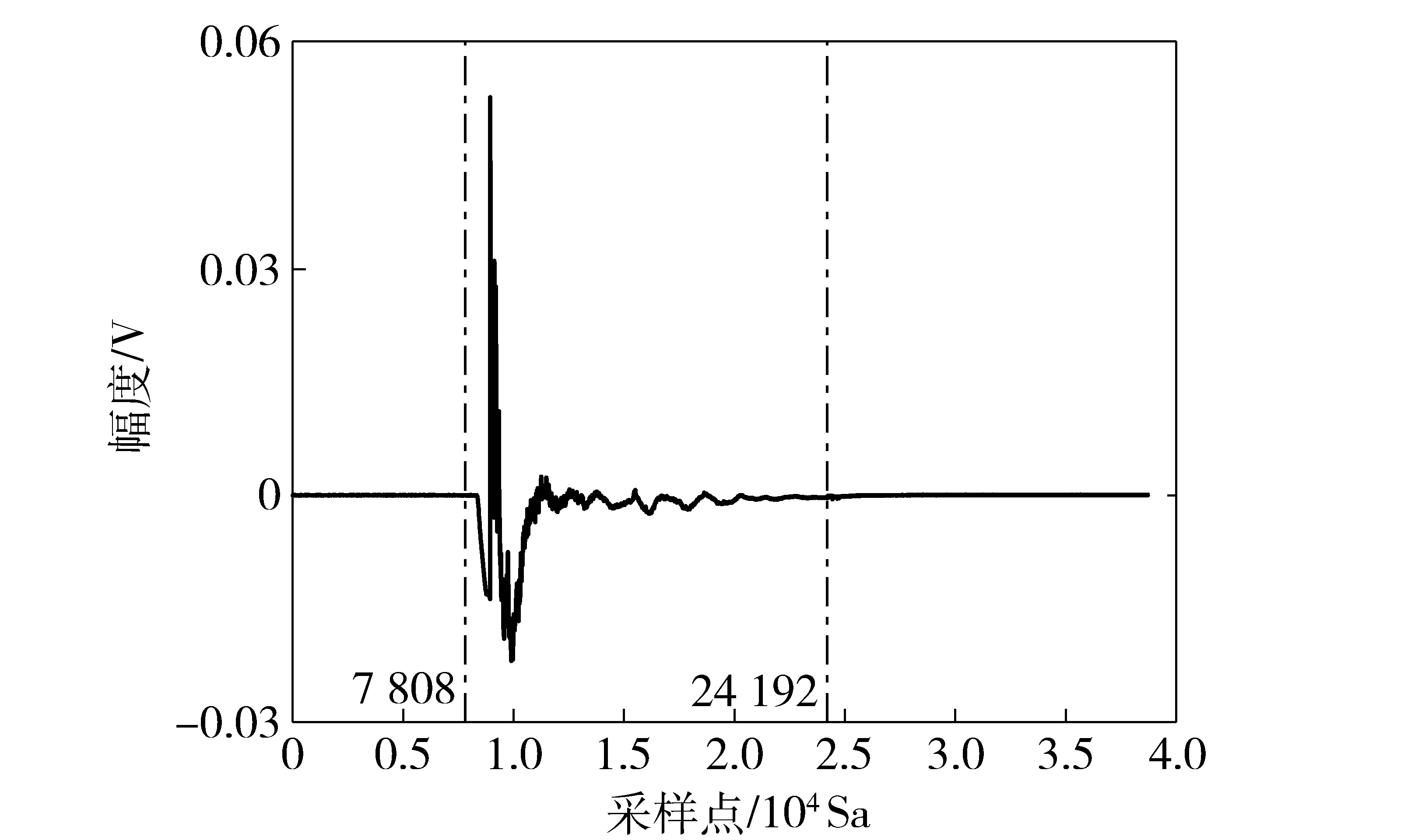
图5 经过算法后数据波形Fig.5 Data waveform after processing
依据重建信息,对被抽取后数据段进行线性插值恢复。其中图6(b)为重建数据及瞬态信号附近50 ms展开,其与图4(b)对应比较可见重建后波形与原瞬态信号展开波形无明显差别。图7(c)为此50 ms的重建数据相较原数据误差,由图7(c)中可以看出,瞬态信号持续时间内的数据完整保留,瞬态信号前后时间内误差小于0.1 mV,与噪声量级相当。全部重建数据相较原始数据的最大误差为0.083 45 mV.

图6 瞬态信号重建波形Fig.6 Reconstruction waveform of transient signal

图7 瞬态位置50 ms时长重建误差Fig.7 Reconstructed error of transient position in 50 ms
如前所述,本次测试中系统中48个通道单次测试产生960 MB数据,经自适应变频算法后,数据压缩比为128,全系统数据产生速率符合千兆以太网传输速率,可进行实时传输,同时瞬态信号部分数据不被压缩,完整保留,非瞬态信号部分最大误差为0.083 45 mV,本次测试系统满量程为±100 mV,即最大相对误差小于0.1%FS. 可见,该算法可以在保证瞬态数据完整的情况下对数据进行极大的压缩。减少冗余数据对存储、传输和数据处理环节的压力。
3.2 对比处理方式对重建精度的影响
如3.1节所述,为一次自适应压缩实际应用,其中抽取方式采用等间隔采样,重建方式为线性插值重建。由处理结果可见,算法可对数据进行大比例压缩的同时,仅在非瞬态信号数据段产生较小误差。同时采用本文提出的多种抽样方式和重建方式进行组合实验。得出结果见表1.
由表1可以看出,对多组数据采用本文算法进行数据压缩均可减少冗余数据,其压缩比例通常大于33,同时瞬态信号部分可以无误差完整保留,非瞬态信号部分最大误差均不超过0.5%FS.
横向对比可以看出,在采用相同的重建方式时,取平均抽样结果的最大误差、误差绝对值均值和误差标准差均小于等间隔抽样。由此可知,取平均抽样方式抽取得到的新数列在重建时误差更小。但由于等间隔抽样方式易于实现,同时可保证较好重建精度,在对非瞬态部分精度要求并非特别苛刻的环境可采用较为简单的等间隔抽样方式。
纵向对比可以看出,在对等间隔采样结果进行重建时,样条插值重建结果全面优于线性插值,由样条插值和分段线性插值特征可知,样条插值结果在连接点处更平滑,可减少由于重建波形存在第一类间断点而带来的重建误差。但由于取平均抽样中,新的数据点并非原始数据,采用样条插值并不能有效提高精度。由此可知,在抽取结果为原始数据的子集时,采用样条插值进行重建可以更好地表达原采集数据形态。
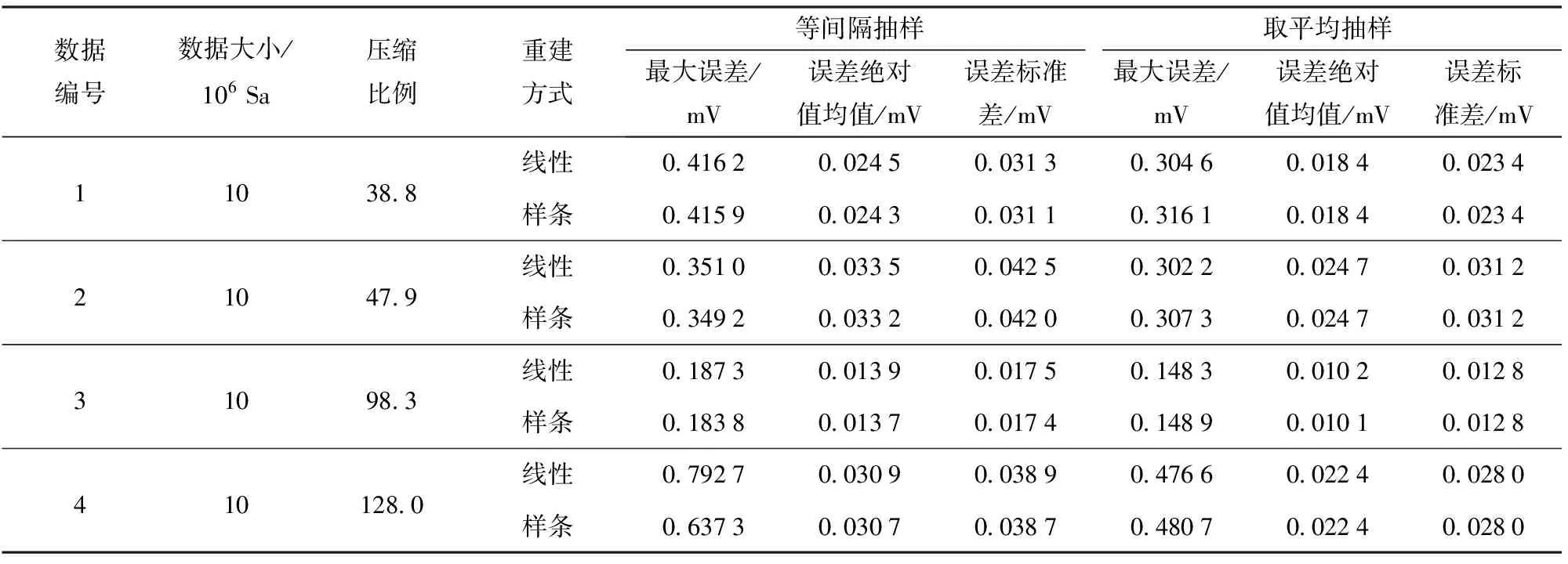
表1 不同抽样方式和重建方式组合误差结果Tab.1 Errors of different sampling methods and reconstruction methods
通过多次实验数据对比得出,经过本文自适应压缩算法处理后,相关项目瞬态场实验数据压缩比例均大于33,同时保证瞬态信号持续时间内数据完整保留,非瞬态信号持续时间内引入误差小于0.5%FS. 有效提高系统对瞬态信号测试效率。
4 结论
综上所述,本文提出自适应压缩算法,依据门限条件,系统自行确定瞬态信号发生时刻,对冗余数据进行二次抽取,在满足奈奎斯特采样定理的前提下减少冗余数据,从而达到减少其占用的存储空间和传输带宽。可以解决在多通道瞬态信号测试过程中,传统采集系统产生的大量冗余数据对数据存储、传输和处理带来的不必要压力等问题。在瞬态测试领域,尤其在多通道大规模瞬态场测试和长时间突发瞬态信号记录领域有一定的研究和应用价值。
References)
[1] 孙鹏,刘平香,徐百灵.瞬态信号检测方法的研究[J]. 舰船科学技术, 2005, 27(3): 72-76. SUN Peng, LIU Ping-xiang, XU Bai-ling. The research on the detection of transient signal[J]. Ship Science and Technology, 2005, 27(3): 72-76.(in Chinese)
[2] 朱代柱.水下瞬态信号的检测与识别[J]. 声学技术, 2007, 26(4): 592-596. ZHU Dai-zhu. Detection and discrimination of underwater transient signal[J]. Technical Acoustics,2007, 26(4): 592-596. (in Chinese)
[3] Jia Z H, Wang W L. Wireless distributed test system based on transient pressure signal detection and recognition[J]. Journal of Measurement Science and Instrumentation, 2016, 7(1): 18-23.
[4] Liu K Y, Siew W H, Stewart R W, et al. High-speed distributed acquisition network for fast transient measurement[J]. IET Generation Transmission & Distribution, 2014, 8(7):1254-1262.
[5] 张世文,龙建华,贾宏志,等. 平面冲击波在有机玻璃中的衰减测试及数值模拟[J]. 兵工学报, 2016, 37(7): 1214-1219. ZHANG Shi-wen, LONG Jian-hua, JIA Hong-zhi, et al. Measuring and numerical simulation of attenuation of planar shock wave in PMMA[J].Acta Armamentarii, 2016, 37(7): 1214-1219.(in Chinese)
[6] 张荣,陈颖,黄海莹,等.超高速多通道瞬态测试系统软硬件设计技术研究[J].计算机测量与控制, 2014, 22(11): 3500-3503. ZHANG Rong, CHEN Ying, HUANG Hai-ying, et al. Design technique research on ultra-high speed multi-channel transient testing system[J]. Computer Measurement & Control, 2014, 22(11): 3500-3503. (in Chinese)
[7] Yuan H, Yang Q, Siddiqui A A. Design of portable high-speed data acquisition device for transient measurements[C]∥Proceedings of 2009 9th International Conference on Electronic Measurement & Instruments. Beijing: Electronic Measurement Technology, 2009: 846-849.
[8] 张威峰,靳鸿,陈昌鑫. 负延迟和变频采样的瞬态信号低冗余存储方法[J]. 探测与控制学报, 2014, 36(6): 53-56. ZHANG Wei-feng, JIN Hong, CHEN Chang-xin. Negative delay and frequency-change sampling transient signal redundant storage method[J]. Journal of Detection & Control, 2014, 36(6): 53-56. (in Chinese)
[9] 陈昌鑫,靳鸿,马铁华. 冲击加速度存储测试的变频采样策略分析[J]. 爆炸与冲击, 2015, 35(4): 501-506. CHEN Chang-xin, JIN Hong, MA Tie-hua. Analysis of frequency-change sampling strategy for impact acceleration storage measurement[J]. Explosion and Shock Waves, 2015, 35(4): 501-506. (in Chinese)
[10] 舒跃飞, 李新娥,刘雪飞,等. 瞬态高压多点压力测试系统[J]. 中国测试,2016, 42(3): 67-72. SHU Yue-fei, LI Xin-e, LIU Xue-fei, et al. Transient high-pressure multi-point pressure testing system[J]. China Measurement & Test, 2016, 42(3):67-72. (in Chinese)
[11] IEEE-Institute of Electrical and Electronics Engineers INC. Physical layer parameters and specifications for 1 000 Mb/s operation over 4-pair of category 5 balanced copper cabling, Type 1000BASE-T[S]. Washington: IEEE Computer Society, 1999.
[12] Sadovskiy M A. Selected works: geophysics and physics of explosion[M]∥ Sadovskiy M A. Mechanical effects of air shockwaves from explosions according to experiments. Moscow: Nauka Press, 2004:47-52.
[13] Walter P L. Shock and blast measurement-rise time capability of measurement systems[EB/OL]. http:∥www.pcb.com/techsupport/docs/pcb/TN-11-0904_Calculating_Rise_Time.pdf.
Adaptive Frequency-change Sampling Strategy ofMulti-channel Transient Signal Test
WANG Xiao, HAN Tai-lin, ZHANG Yong-li, LIU Xuan, WANG Yi-jun, GONG Yu-lin
(College of Electronic and Information Engineering, Changchun University of Science and Technology,Changchun 130022, Jilin, China)
In the multi-channel transient signal test, the redundant data test by the conventional test system at long time and high sampling rate causes the storage and transmission problems. An adaptive frequency-change sampling strategy is presented to solve these problems. The algorithm lets the test system acquire the primary data at the same sample rate as the traditional test systems can, and divides the data in time. According to the frequency domain characteristics of signal in each segment, the occurring time and duration of transient signal are determined. The non-transient signals are resampled to reduce the redundant data, and the transient segments can be saved completely. The data compression ratio is more than 33 after the data is processed by the algorithm, while the duration data of transient signal is fully retained, and the maximum error of the non-transient segments are less than 0.5FS. The experimental results show that the algorithm can effectively reduce the redundant data in transient test.
information processing technology; transient signal test; adaptive frequency convention; data pre-processing
2016-11-16
总装备部装运局科研项目(2013年)
王啸(1990—),男,博士研究生。E-mail: wangx_work@126.com
韩太林(1969—),男,教授,博士生导师。E-mail:hantl@cust.edu.cn
TP274+.1
A
1000-1093(2017)06-1161-07
10.3969/j.issn.1000-1093.2017.06.016
