数形结合在新课标导数与函数中的渗透

广东省珠海市实验中学(519090) 周玲玲

数形结合在新课标导数与函数中的渗透

广东省珠海市实验中学(519090) 周玲玲

“数与形本是两依倚,焉能分作两边飞,数缺形时少直观,形少数时难入微.”在这首诗中华罗庚先生指出了数与形相互之间的关系,揭示了数形结合思想方法的本质和重要性.数形结合思想是中学数学中七个常用基本思想方法之一.

在高考数学试题中,数形结合思想渗透方方面面.题目主要出现在函数、导数、解析几何等题目上,把图象作为工具、载体,不仅可以直观,而且易于寻找解题的途径和突破口,以此寻求解题思路或制定解题方案.从近年高考课标卷来看,对数形结合等思想方法的考查,是对数学知识在更高层次的抽象和概括能力的考查,是对学生思维品质和数学技能的考查,是课标课程高考明确的一个命题方向.本文从以下几个方面结合相关高考试题谈谈数形结合思想方法在函数与导数中的渗透.

渗透一由恒成立问题求参数取值范围问题

例1(2015课标全国I,理12).设函数f(x)=ex(2x-1)-ax-a,其中a＜ 1,若存在唯一的整数x0,使得f(x0)＜0,则a的取值范围是( )

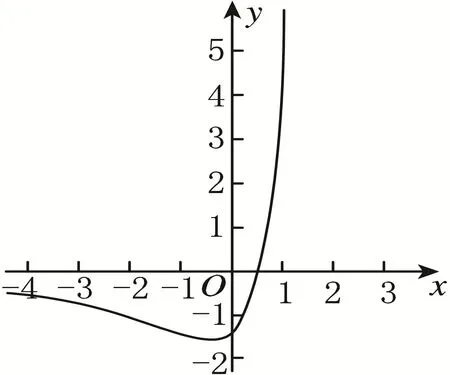
图1

[解析]令g(x)=ex(2x-1),则g′(x)=ex(2x+1),由g(x) ＞ 0得x＞-,由 g′(x)＜ 0得 x ＜故函数g(x)在上单调递减,在上单调 递 增. 又 函 数 g(x)在 x ＜时,g(x)＜0,在x＞时,g(x)＞0,所以其大致图像如图1.直线y=ax-a过点(1,0).若a≤0,则f(x)＜0的整数解有无穷多个,因此只能a＞0.结合函数图像可知,存在唯一的整数x0,使得f(x0)＜0,即存在唯一的整数x0,使得点(x0,ax0-a)在点(x0,g(x0))的上方,则x0只能是0,故实数a应满足即解得≤a＜1.故实数a的取值范围

点评:本题通过数与形的相互转化来解决数学问题的一种重要思想方法.数形结合思想通过“以形助数,以数解形”,使复杂问题简单化,抽象问题具体化,能够变抽象思维为形象思维,有助于把握数学问题的本质,它是数学的规律性与灵活性的有机结合.

渗透二确定零点的个数(方程根的个数或图象的交点个数

图2

例2 (2016课标全国卷I,理21(1))已知函数f(x)=(x-2)ex+a(x-1)2有两个零点,求a的取值范围;

[解析]依题意得 f(x)=(x-2)ex+a(x-1)2=0时有两个根,因为x=1不是根,从而方程有两个根,令则因为(x-2)2+1＞0,ex＞0,当x＜1时, g′(x) ＜ 0, g(x) 在 (1,+∞) 上单调递增,且过点(0,2);当x＞ 1时,g′(x)＜ 0,g(x)在(1,+∞)上单调递减,且过点(2,0)根据g(x)的解析式可以看出它有一条渐近线x=1,g(x)的大致图像如图2.由图易知a=h(x)有两根时,a的取值范围为(0,+∞).

点评:本题本质上是把方程实根的个数转化为两个函数的图象交点个数,体现了转化与化归思想、数形结合思想,从而分离参数a,利用导数可以模拟g(x)的大致图像,一般从“形”入手更为直观,利用其图象特征,就可以找到解题思路,利用图象进行分析.当然还需相应的数学具体变形与运算,这样才体现数形结合,争取做到胸中有图,见数想图,以开拓自己的思维视野.

渗透三证明不等式

例3(2007全国卷II)函数f(x)=x3-x.设a＞0,如果过点(a,b)可作曲线y=f(x)的三条切线,证明-a＜b＜f(a).

图3

[解析]可设其中一条切线的切点为p(t,t3-t),则切线为y-(t3-t)=(3t2-1)(x-t)由切线过(a,b)得,b=(3t2-1)a-2t3,即2t3-3at2+a+b=0有三个相异实数根.令g(t)=2t3-3at2+a+b则有三个相异实数根,g′(t)=6t2-6at=6t(t-a).如图可知:即

数形结合包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:一是借助形的生动性和直观性来阐明数之间的联系,即以形作为手段,数作为目的,比如应用函数的图象来直观地说明函数的性质;二是借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的.数形结合的思想,其实质是将抽象的数学语言与直观的图象结合起来,关键是代数问题与图形之间的相互转化,它可以使代数问题几何化,几何问题代数化.总而言之,数形结合思想方法的应用是有条件的,若问题所涉及的“数”具有“形”的特征,或“形”具有“数或式”的特征,则可以应用数形结合的思想方法解之,当然这种特征要依赖于基本的数学知识和数学概念,依赖于良好的思维品质和一定想像力这一前提.

《考纲》指出“数学科的命题,在考查基础知识的基础上,注重对数学思想思想方法的考查,注重对数学能力的考查”,数形结合的思想方法在高考中占有非常重要的地位,灵活运用数形结合的思想方法,可以有效提升思维品质和数学技能.从目前高考“重视思想方法,注重通法,淡化技巧”的命题原则来看,我们在教学上要更加重视学生在数形结合的思想方法上的训练.